1. Fonctions usuelles de R pour les tests
Rappeler quels sont les "grands tests classiques", paramétriques ou non. Quelles sont les fonctions usuelles de R associées ?
Comment récupère-t-on la p-value ? Et la valeur de la statistique de test ? Et son intervalle de confiance ?
Application : Donner l'intervalle de confiance de la variable Length pour les données lea.dar.
Pour comparer deux QT, on utilise un test d'hypothèse paramétrique ou non paramétrique suivant la normalité de la distribution des échantillons : pour des données normales non appariées, on utilise le test t de Student qui est équivalent à une ANOVA à un facteur ; pour des données normales appariées, on utilise le test t de Student adapté aux données appariées ; pour des données non normales non appariées, on utilise le test de Mann-Whitney ; pour des données non normales appariées, on utilise le test de Wilcox.
Voici le tableau résumé de ces divers cas pour comparer deux QT :
|
|
Données non appariées |
Données appariées |
| Données normales |
test t de Student (ou anova) |
test t de Student adapté |
| Données non normales |
test de Mann-Whitney |
test de Wilcox |
Pour comparer plus de deux QT, on utilise comme tests d'hypothèse paramétriques des anova, ancova, manova et autre mancova (donc pour des données normales) ; dans le cas non paramétrique, on utilise le test de Kruskal-Wallis pour des données non normales non appariées et le test de Friedman pour des données non normales appariées.
Voici le tableau résumé de ces divers cas pour comparer plus de deux QT :
|
|
Données non appariées |
Données appariées |
| Données normales |
anova, ancova etc. |
anova, ancova etc. |
| Données non normales |
test de Kruskal-Wallis |
test de Friedman |
En termes de graphiques, il est d'usage de tracer des boites à moustaches simultanées des QT, avec éventuellements des encoches (qui illustrent le test d'égalité des médianes).
Il faut noter que, pour plus de deux QT, lorsque les tests d'hypothèses montrent des différences significatives entre les QT, on doit effectuer des tests post hoc pour déterminer quelles QT sont significativement différentes. De plus, ces comparaisons s'effectuent plutôt sur des groupes à l'intérieur d'une même QT que sur des QT différentes.
Pour étudier conjointement deux QL, on effectue un tri croisé puis un test d'indépendance du khi-deux sur ce tri croisé si les effectifs présents le permettent. En termes de graphiques, il est d'usage de tracer les histogrammes des effectifs des deux tris à plats et du tri croisé dans les deux sens afin de détecter d'éventuelles dépendances (changements de profils).
Voici un tableau résumé avec les principaux tests et les fonctions R associées :
Les tests non paramétriques s'utilisent lorsque les conditions de normalité, d'égalité des variances homoscédasticité etc. ne sont pas respectées. Leur utilisation est semblable à celles des test paramétriques. Ainsi wilcox.test(x,y) se substitue à t.test(x,y) et friedman.test(y ~ x) est semblable à anova(lm(y ~ x)).
Lorsqu'on connait la fonction de R qui réalise le test demandé, il faut regarder le nom des composantes de la liste obtenue par application de cette fonction. Les noms sont obtenus via la fonction names(). On peut alors extraire avec le symbole dollar la composante désirée :
# lecture des données
url <- "http://www.info.univ-angers.fr/~gh/Datasets/lea.dar"
lea <- read.table(url,header=TRUE,row.names=1)
lng <- lea$length
# intervalle de confiance via la fonction t.test()
print(t.test(lng))
# récupération de cet intervalle
rdt <- t.test(lng)
print(names(rdt))
cat("\n l'intervalle de confiance est donc ",rdt$conf.int,"\n")
# récupération de la p-value
pval <- rdt$p.value
cat("\nla p-value est ",pval,"\n")
# avec nos fonctions :
# chargement des fonctions gh
source("http://forge.info.univ-angers.fr/~gh/wstat/statgh.r",encoding="latin1")
icmQT(lng)
One Sample t-test
data: lng
t = 38.4601, df = 772, p-value < 2.2e-16
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
195.1897 216.1868
sample estimates:
mean of x
205.6882
[1] "statistic" "parameter" "p.value" "conf.int" "estimate" "null.value" "alternative" "method" "data.name"
l'intervalle de confiance est donc 195.1897 216.1868
la p-value est 1.376861e-181
(gH) version 4.87
fonctions d'aides : lit() fqt() fql() ic() fapprox() chi2() fcomp() datagh()
taper aide() pour revoir cette liste
[1] 195.1897 216.1868
2. Comparaisons de pourcentages
La parité Femme/Homme est-elle respectée dans les données elf.dar ? On trouvera des informations sur ces données à l'URL elf.htm.
Peut-on considérer que les différents règnes sont représentés équitablement dans les données lea.dar ? Oon trouvera des informations sur ces données à l'URL lea.htm.
L'équirépartition peut se faire via un test de chi-deux sous hypothèse d'indépendance des deux modalités Homme/Femme de la variable qualitative SEXE. Intuitivement, la répartition en à peu près deux tiers de femmes, un tiers d'hommes laisse à penser qu'il n'y a pas égalité des proportions. Attention : cette intuition peut être trompeuse puisque le test utilise le nombre total d'individus. Voir par exemple la fin de la page pourquoi.
Voici comment avoir rapidement le détail des calculs pour le vérifier avec notre fonction chi2Adeq() ou avec les fonctions classiques de R nommées prop.test() et binom.test().
# chargement de nos fonctions
source("http://www.info.univ-angers.fr/~gh/statgh.r",encoding="latin1")
# lecture des données
elf <- lit.dar("http://www.info.univ-angers.fr/~gh/Datasets/elf.dar")
# tri à plat de la variable SEXE
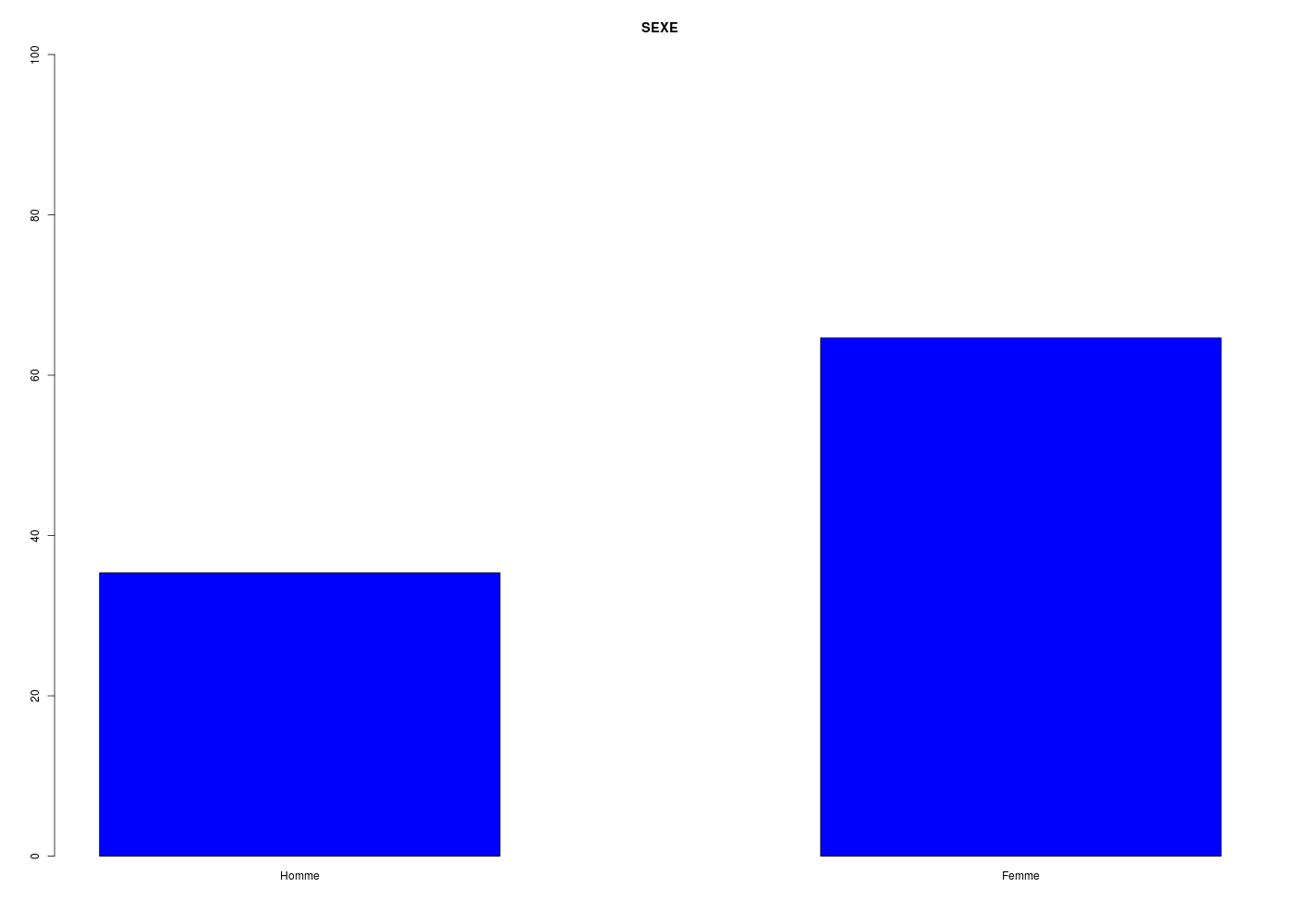
decritQL("SEXE",elf$SEXE,c("Homme","Femme"),TRUE)
sexe <- factor(elf$SEXE,levels=0:1,labels=c("Homme","Femme"))
decritQLf("SEXE",sexe,TRUE,testequi=TRUE)
# test de l'égalité des proportions (3 moyens)
chi2Adeq(vth=c(49,50),vobs=c(35,64))
print( binom.test(x = 64,n = 99) )
print( prop.test(x = 64,n = 99) )
# graphiques pour comparer les distributions
# théoriques et pratiques
countRes <- t(cbind(table(elf$SEXE),c(49,50)))
echantillons <- c("ELF","Théorique")
row.names(countRes) <- echantillons
modalites <- c("Homme","Femme")
colnames(countRes) <- modalites
couleurs <- c("blue","red")
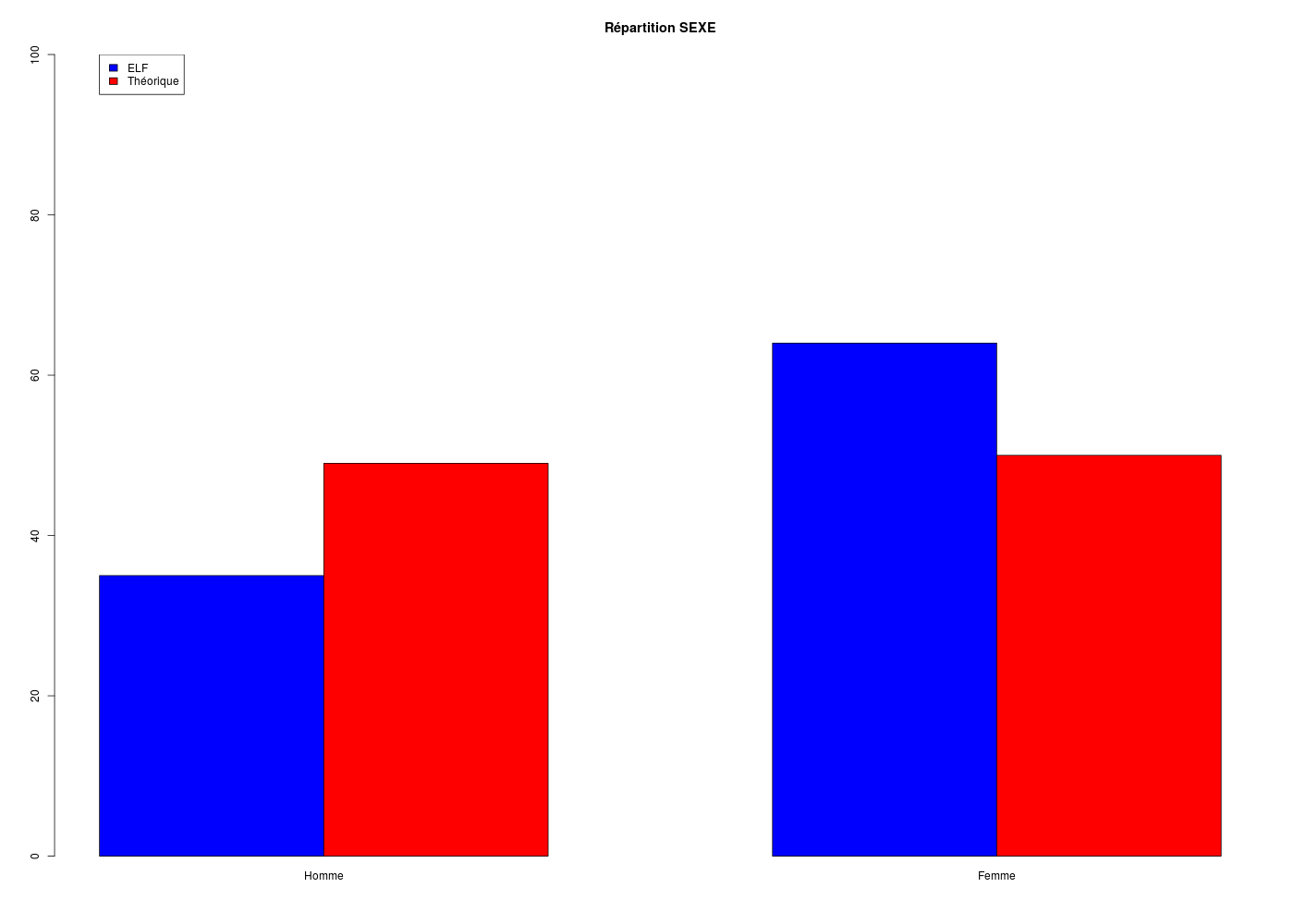
barplot(countRes,beside = TRUE,col=couleurs,main="Répartition SEXE",ylim=c(0,100))
legend(x=1,y=100,fill=couleurs,legend=echantillons)
(gH) version 4.87
fonctions d'aides : lit() fqt() fql() ic() fapprox() chi2() fcomp() datagh()
taper aide() pour revoir cette liste
TRI A PLAT DE : SEXE (ordre des modalités)
Homme Femme Total
Effectif 35 64 99
Cumul Effectif 35 99 99
Frequence (en %) 35 65 100
Cumul fréquences 35 100 100
VARIABLE : SEXE (par fréquence décroissante)
Femme Homme Total
Effectif 64 35 99
Cumul Effectif 35 99 99
Frequence (en %) 65 35 100
Cumul fréquences 65 100 100
[1] "Homme" "Femme"
TRI A PLAT DE : SEXE (ordre des modalités)
Homme Femme Total
Effectif 35 64 99
Cumul Effectif 35 99 99
Frequence (en %) 35 65 100
Cumul fréquences 35 100 100
VARIABLE : SEXE (par fréquence décroissante)
Femme Homme Total
Effectif 64 35 99
Cumul Effectif 35 99 99
Frequence (en %) 65 35 100
Cumul fréquences 65 100 100
[1] "Homme" "Femme"
CALCUL DU CHI-DEUX D'ADEQUATION
Valeurs théoriques 49.5 49.5
Valeurs observées 35 64
Valeur du chi-deux 8.494949
Chi-deux max (table) à 5 % 3.841459 pour 1 degrés de liberté ; p-value 0.003561337
décision : au seuil de 5 % on peut rejeter l'hypothèse
que les données observées correspondent aux valeurs théoriques.
Contributions au chi-deux
Ind. The Obs Dif Cntr Pct Cumul
1 49.5 35 14.5 4.247475 50 4.247475
2 49.5 64 -14.5 4.247475 50 8.494949
CALCUL DU CHI-DEUX D'ADEQUATION
Valeurs théoriques 49 50
Valeurs observées 35 64
Valeur du chi-deux 7.92
Chi-deux max (table) à 5 % 3.841459 pour 1 degrés de liberté ; p-value 0.004889127
décision : au seuil de 5 % on peut rejeter l'hypothèse
que les données observées correspondent aux valeurs théoriques.
Exact binomial test
data: 64 and 99
number of successes = 64, number of trials = 99, p-value = 0.004641
alternative hypothesis: true probability of success is not equal to 0.5
95 percent confidence interval:
0.5439647 0.7399466
sample estimates:
probability of success
0.6464646
1-sample proportions test with continuity correction
data: 64 out of 99, null probability 0.5
X-squared = 7.9192, df = 1, p-value = 0.004891
alternative hypothesis: true p is not equal to 0.5
95 percent confidence interval:
0.5432921 0.7381205
sample estimates:
p
0.6464646
Pour les règnes dans lea.dar le plus simple est de passer par notre fonction decritQLf() avec son paramètre de test d'équirépartition mis à vrai (TRUE) :
# lecture des données
url <- "http://www.info.univ-angers.fr/~gh/Datasets/lea.dar"
lea <- read.table(url,header=TRUE,row.names=1)
reign <- lea$reign
# description du facteur et test d'équirépartition
decritQLf(titreQL = "Règne",nomFact = reign,graphique = TRUE,testequi = TRUE)
TRI A PLAT DE : Règne (ordre des modalités)
Alveolata Bacteria Euryarchaeota Fungi Metazoa Parabasalidea Viridiplantae Total
Effectif 1 38 1 11 23 1 698 773
Cumul Effectif 1 39 40 51 74 75 773 773
Frequence (en %) 0 5 0 1 3 0 90 99
Cumul fréquences 0 5 5 7 10 10 100 99
VARIABLE : Règne (par fréquence décroissante)
Viridiplantae Bacteria Metazoa Fungi Alveolata Euryarchaeota Parabasalidea Total
Effectif 698 38 23 11 1 1 1 773
Cumul Effectif 1 39 40 51 74 75 773 773
Frequence (en %) 90 5 3 1 0 0 0 99
Cumul fréquences 90 95 98 100 100 100 100 99
[1] "Alveolata" "Bacteria" "Euryarchaeota" "Fungi" "Metazoa" "Parabasalidea" "Viridiplantae"
CALCUL DU CHI-DEUX D'ADEQUATION
Valeurs théoriques 110.4286 110.4286 110.4286 110.4286 110.4286 110.4286 110.4286
Valeurs observées 1 38 1 11 23 1 698
Valeur du chi-deux 3657.928
Chi-deux max (table) à 5 % 12.59159 pour 6 degrés de liberté ; p-value 0
décision : au seuil de 5 % on peut rejeter l'hypothèse
que les données observées correspondent aux valeurs théoriques.
Contributions au chi-deux
Ind. The Obs Dif Cntr Pct Cumul
1 110.4286 1 109.42857 108.4376 2.964455 108.4376
2 110.4286 38 72.42857 47.5049 1.298683 155.9425
3 110.4286 1 109.42857 108.4376 2.964455 264.3802
4 110.4286 11 99.42857 89.5243 2.447405 353.9045
5 110.4286 23 87.42857 69.2190 1.892301 423.1235
6 110.4286 1 109.42857 108.4376 2.964455 531.5611
7 110.4286 698 -587.57143 3126.3665 85.468245 3657.9276
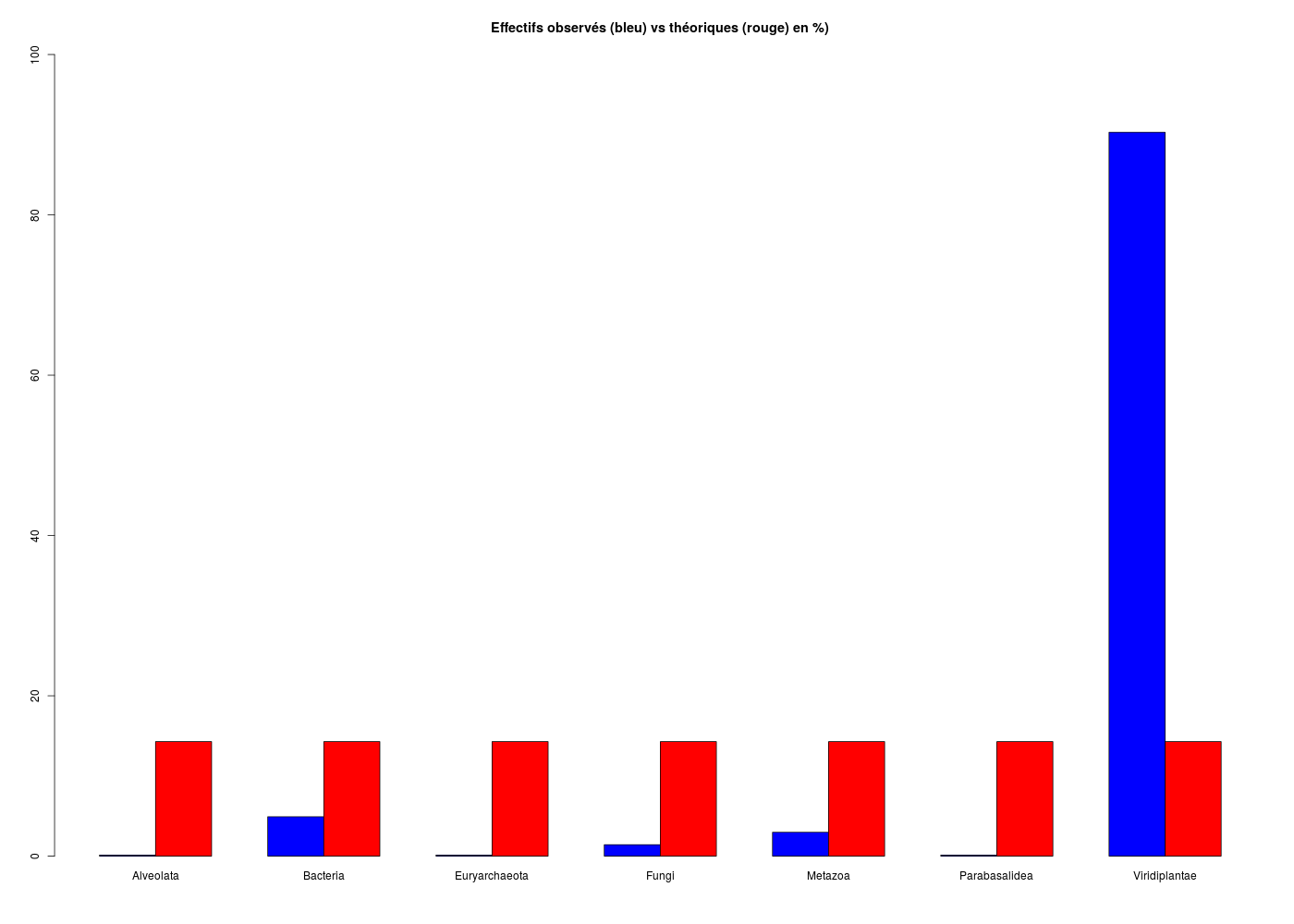
On en déduit (évidemment !) qu'il n'y a pas équirépartition, le règle très majoritaire étant celui des plantes (Viridiplantae).
3. Comparaison d'une moyenne à une référence
Après avoir analysé la variable Length des données lea.dar (on trouvera des informations sur ces données à l'URL lea.htm), peut-on affirmer qu'en moyenne une protéine LEA comporte 361 résidus d'acides aminés ? Au passage, d'où provient cette valeur 361 ?
Avant de réaliser ce test de conformité de moyenne à une valeur théorique, cela ne fait pas de mal d'analyser la variable Length :
# lecture des données
source("http://www.info.univ-angers.fr/~gh/statgh.r",encoding="latin1")
lea <- lit.dar("http://www.info.univ-angers.fr/~gh/Datasets/lea.dar")
# description des données
decritQT("Longueur des protéines de LEAPDB",lea$length ,"aa",TRUE)
# test de conformité
print(t.test(lea$length,mu=361))
(gH) version 4.87
fonctions d'aides : lit() fqt() fql() ic() fapprox() chi2() fcomp() datagh()
taper aide() pour revoir cette liste
DESCRIPTION STATISTIQUE DE LA VARIABLE Longueur des protéines de LEAPDB
Taille 773 individus
Moyenne 205.6882 aa
Ecart-type 148.6924 aa
Coef. de variation 72 %
1er Quartile 130.0000 aa
Mediane 168.0000 aa
3eme Quartile 236.0000 aa
iqr absolu 106.0000 aa
iqr relatif 63.0000 %
Minimum 68 aa
Maximum 1864 aa
Tracé tige et feuilles
The decimal point is 2 digit(s) to the right of the |
0 | 77777888888899999999999999999999999999999999999999999999999999999999
1 | 00000000000000000000000000000000000000000000000111111111111111111111+323
2 | 00000000000000000000000000001111111111111111222222222222223333333333+107
3 | 000000011111222223333344444445556666788889999
4 | 0011111112223444556666777778889
5 | 0122455667888
6 | 22344588
7 | 234
8 | 5
9 |
10 |
11 |
12 | 4
13 |
14 | 3
15 | 1
16 |
17 |
18 | 6
One Sample t-test
data: lea$length
t = -29.0406, df = 772, p-value < 2.2e-16
alternative hypothesis: true mean is not equal to 361
95 percent confidence interval:
195.1897 216.1868
sample estimates:
mean of x
205.6882
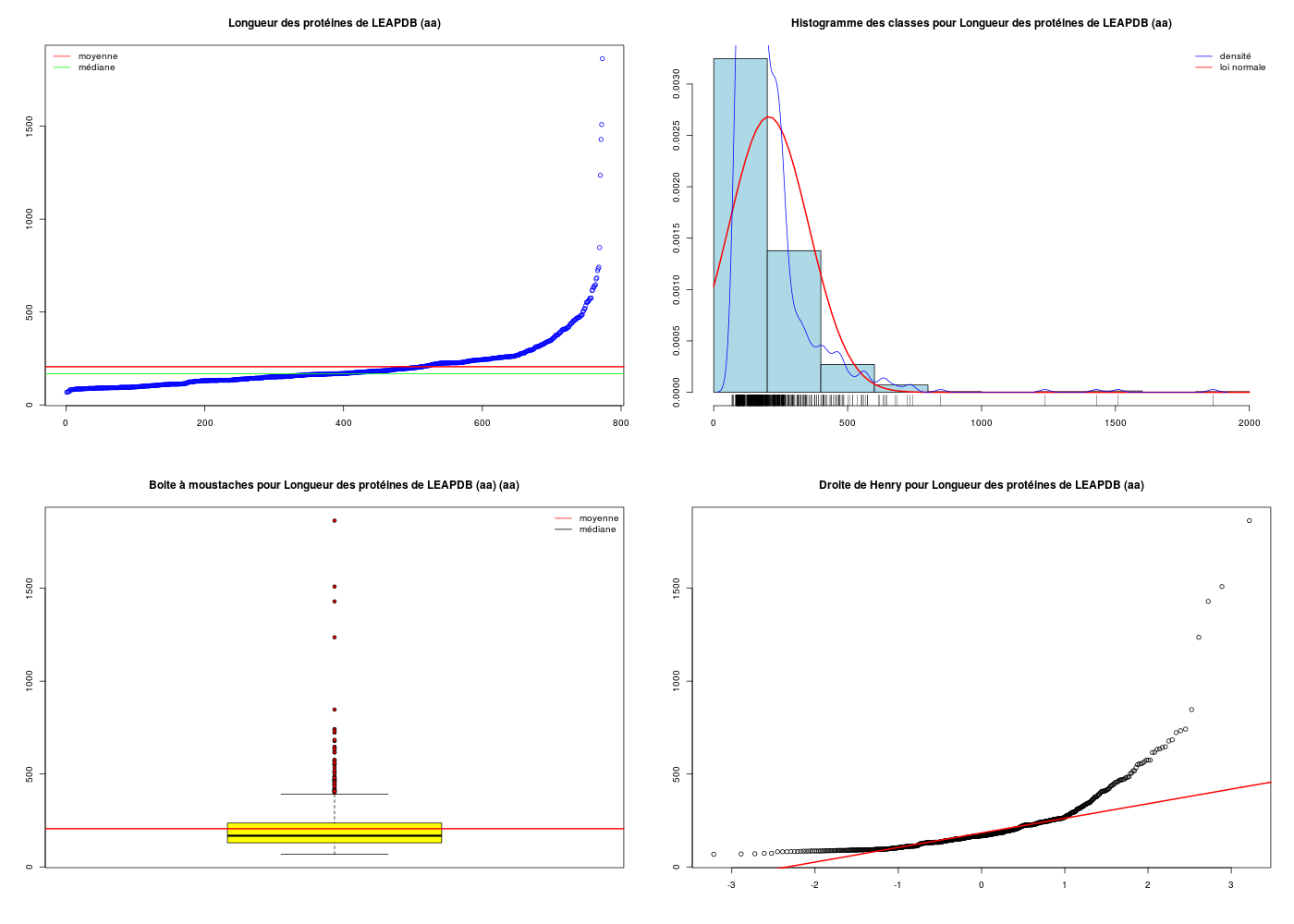
La p-value du test de conformité très inférieure à 0,05 indique qu'on doit rejeter l'hypothèse selon laquelle en moyenne une protéine LEA comporte 361 résidus d'acides aminés.
La valeur 361 (qui est en fait une valeur de médiane et non pas de moyenne, ce qui est sans doute plus "adapté") provient de l'article très intéressant de Brocchieri et Karlin (Nucleic Acids Research, 2005) -- dont une copie locale est ici -- dans lequel on peut lire : The median length of the proteins annotated among Eukaryotes (361 amino acids) is much higher than in Bacteria (267 amino acids).
4. Comparaisons de moyennes et ANOVA, paramétrique ou non paramétrique
On voudrait comparer les distributions d'ages pour les femmes et les hommes dans les données elf.dar (on trouvera des informations sur ces données à l'URL elf.htm). Quels tests envisager ? Comment choisir ici entre tests paramétriques et non paramétriques ?
Il y a bien sûr plusieurs façons de constituer le vecteur des ages des hommes et celui des femmes ou les sous-ensembles correspondants :
# lecture des données
source("http://www.info.univ-angers.fr/~gh/statgh.r",encoding="latin1")
elf <- lit.dar("http://www.info.univ-angers.fr/~gh/Datasets/elf.dar")
# décomposition en sous-groupes d'hommes et de femmes
# 1. par filtre explicite dans le vecteur AGE
agesFemmes <- elf$AGE[ elf$SEXE==1 ]
agesHommes <- elf$AGE[ elf$SEXE==0 ]
cat(" ",length(agesFemmes)," femmes et ",length(agesHommes)," hommes\n\n")
# 2. à l'aide de split on crée une liste avec une composante pour les hommes
# et une composante pour les femmes
decoupe <- with(elf, split(x=AGE,f=SEXE) )
names(decoupe) <- c("Hommes","Femmes")
print(sapply(X=decoupe,F=length))
# 3. avec subset
# sous-ensemble 1
cat("\nFemmes\n")
elfFemmes <- subset(elf,SEXE==1)
print(dim(elfFemmes))
# sous-ensemble 2
cat("\nHommes\n")
elfHommes <- subset(elf,SEXE==0)
print(dim(elfHommes))
(gH) version 4.87
fonctions d'aides : lit() fqt() fql() ic() fapprox() chi2() fcomp() datagh()
taper aide() pour revoir cette liste
64 femmes et 35 hommes
Hommes Femmes
35 64
Femmes
[1] 64 6
Hommes
[1] 35 6
Mais en fait, grâce à la notation ~ (tilde) qui se lit «en fonction de», il n'y a pas besoin de décomposer quoi que ce soit :
# conversion explicite du sexe en variable qualitative ("factor")
elf$SEXE <- factor(elf$SEXE,levels=0:1,labels=c("Hommes","Femmes"))
# test paramétrique
print( t.test(AGE~SEXE,data=elf,var.equal=FALSE) )
print( t.test(AGE~SEXE,data=elf,var.equal=TRUE) )
print( anova(lm(AGE~SEXE,data=elf) ))
# test non-paramétrique
print( wilcox.test(AGE~SEXE,data=elf) )
Welch Two Sample t-test
data: AGE by SEXE
t = 0.2431, df = 74.04, p-value = 0.8086
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-6.363368 8.132118
sample estimates:
mean in group Hommes mean in group Femmes
36.40000 35.51562
Two Sample t-test
data: AGE by SEXE
t = 0.2385, df = 97, p-value = 0.812
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-6.475006 8.243756
sample estimates:
mean in group Hommes mean in group Femmes
36.40000 35.51562
Analysis of Variance Table
Response: AGE
Df Sum Sq Mean Sq F value Pr(>F)
SEXE 1 17.7 17.696 0.0569 0.812
Residuals 97 30176.4 311.097
Wilcoxon rank sum test with continuity correction
data: AGE by SEXE
W = 1195, p-value = 0.5854
alternative hypothesis: true location shift is not equal to 0
Il serait certainement plus raisonnable de commencer par analyser la variable AGE globalement et par sous-groupe avant de décider quoi que ce soit :
# lecture des données
source("http://www.info.univ-angers.fr/~gh/statgh.r",encoding="latin1")
elf <- lit.dar("http://www.info.univ-angers.fr/~gh/Datasets/elf.dar")
# 1. analyse globale de la variable AGE
decritQT("AGE (global)",elf$AGE,"ans",TRUE)
# 2. analyse par sous-groupe
decritQT("AGE (femmes)",elf$AGE[elf$SEXE==1],"ans",TRUE)
decritQT("AGE (hommes)",elf$AGE[elf$SEXE==0],"ans",TRUE)
(gH) version 4.87
fonctions d'aides : lit() fqt() fql() ic() fapprox() chi2() fcomp() datagh()
taper aide() pour revoir cette liste
DESCRIPTION STATISTIQUE DE LA VARIABLE AGE (global)
Taille 99 individus
Moyenne 35.8283 ans
Ecart-type 17.5529 ans
Coef. de variation 49 %
1er Quartile 22.0000 ans
Mediane 29.0000 ans
3eme Quartile 48.5000 ans
iqr absolu 26.5000 ans
iqr relatif 91.0000 %
Minimum 11 ans
Maximum 78 ans
Tracé tige et feuilles
The decimal point is 1 digit(s) to the right of the |
1 | 1223455567778889999
2 | 0011222344555566667778888888999
3 | 0011123556799
4 | 0123446778899
5 | 0002239
6 | 0011222345
7 | 033368
DESCRIPTION STATISTIQUE DE LA VARIABLE AGE (femmes)
Taille 64 individus
Moyenne 35.5156 ans
Ecart-type 18.0273 ans
Coef. de variation 50 %
1er Quartile 21.0000 ans
Mediane 29.5000 ans
3eme Quartile 48.2500 ans
iqr absolu 27.2500 ans
iqr relatif 92.0000 %
Minimum 11 ans
Maximum 76 ans
Tracé tige et feuilles
The decimal point is 1 digit(s) to the right of the |
1 | 123455577889999
2 | 11234455566778889
3 | 011156799
4 | 01446889
5 | 00039
6 | 01123
7 | 03336
DESCRIPTION STATISTIQUE DE LA VARIABLE AGE (hommes)
Taille 35 individus
Moyenne 36.4000 ans
Ecart-type 16.8927 ans
Coef. de variation 46 %
1er Quartile 25.5000 ans
Mediane 29.0000 ans
3eme Quartile 48.0000 ans
iqr absolu 22.5000 ans
iqr relatif 78.0000 %
Minimum 12 ans
Maximum 78 ans
Tracé tige et feuilles
The decimal point is 1 digit(s) to the right of the |
1 | 2678
2 | 00225667888899
3 | 0235
4 | 23779
5 | 22
6 | 02245
7 | 8
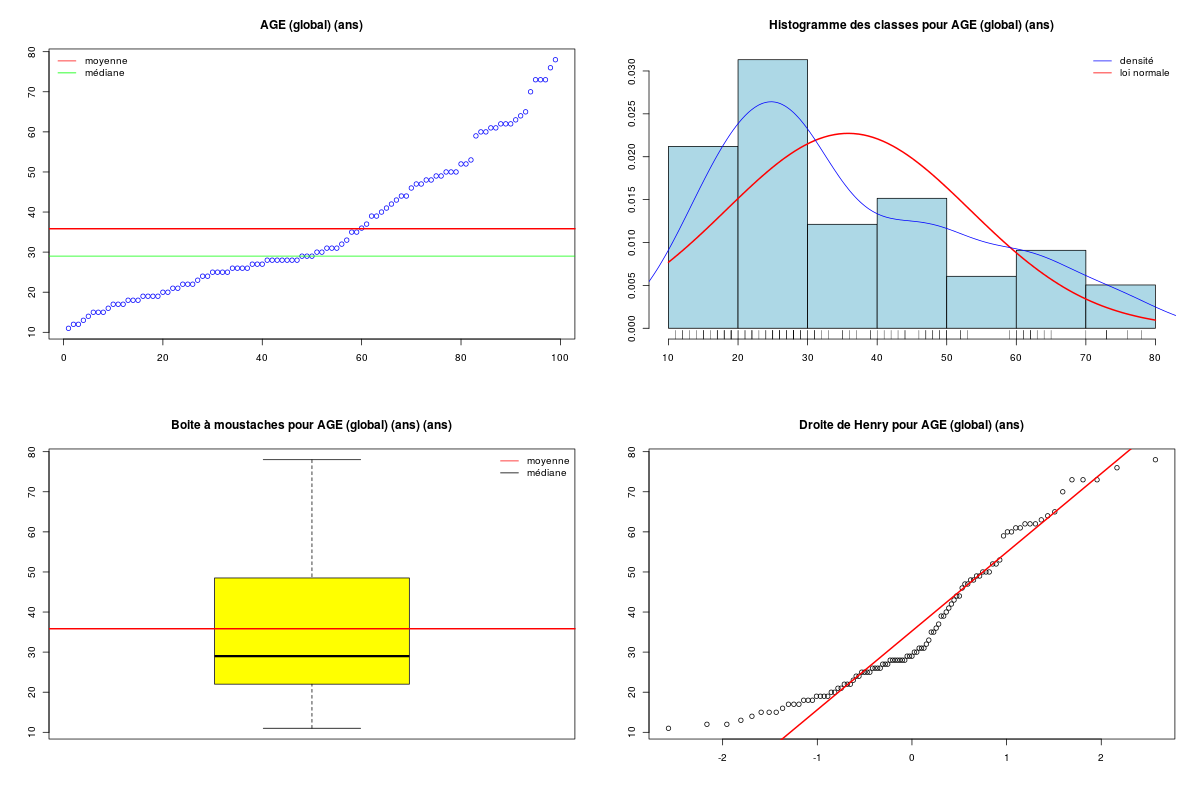
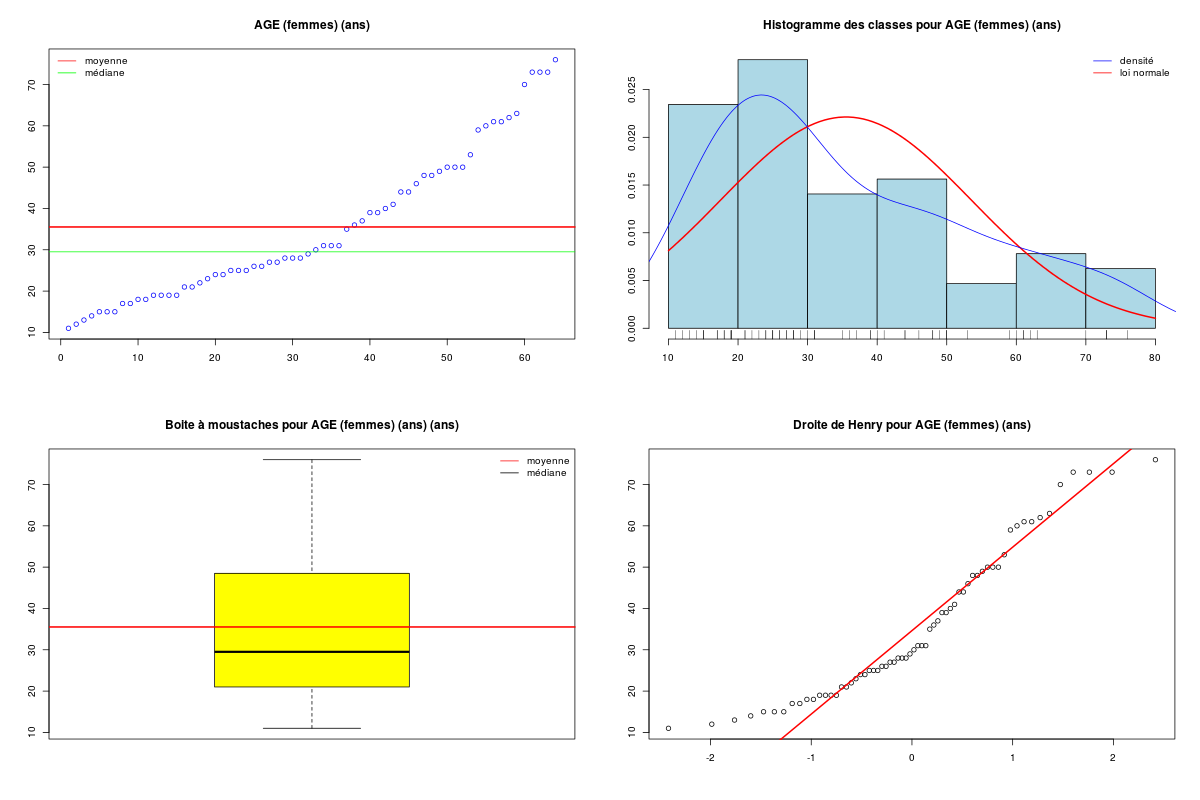
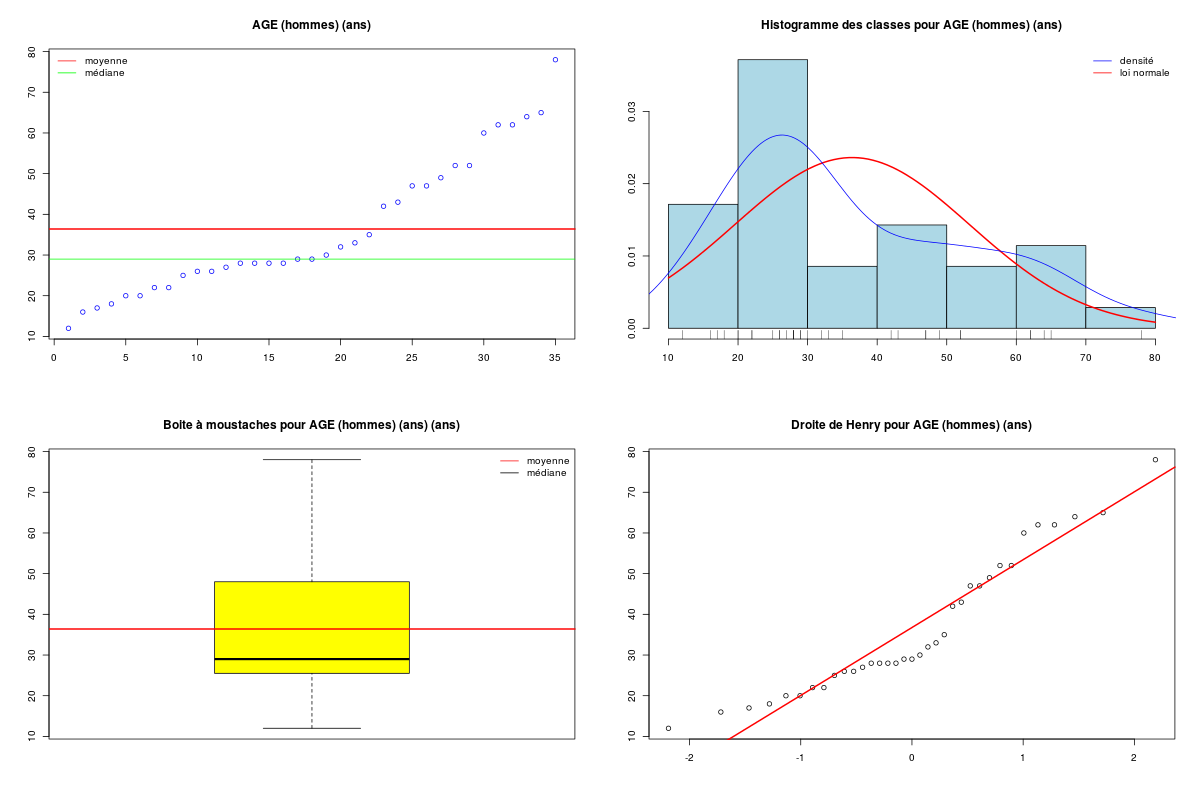
Le peu de données dans le groupe des hommes et la non normalité apparente des données mène à la conclusion qu'il n'est pas conseillé d'utiliser une analyse paramétrique. On utilise donc un test de Wilcox et on trace des boites à moustaches.
# test non-paramétrique
print( wilcox.test(AGE~SEXE,data=elf) )
# boites à moustaches associées
with(elf,
boxplot(AGE~factor(SEXE,levels=0:1,labels=c("Hommes","Femmes"))
,col="yellow",main="AGES (dossier ELF)",ylim=c(10,80))
)
# pour information
with(elf,
boxplot(AGE~factor(SEXE,levels=0:1,labels=c("Hommes","Femmes")),
col="yellow",main="AGES (dossier ELF)",ylim=c(10,80),
plot=FALSE
) # fin de boxplot
) # fin de with
Wilcoxon rank sum test with continuity correction
data: AGE by SEXE
W = 1195, p-value = 0.5854
alternative hypothesis: true location shift is not equal to 0
$stats
[,1] [,2]
[1,] 12.0 11.0
[2,] 25.5 21.0
[3,] 29.0 29.5
[4,] 48.0 48.5
[5,] 78.0 76.0
attr(,"class")
Hommes
"integer"
$n
[1] 35 64
$conf
[,1] [,2]
[1,] 22.99095 24.06875
[2,] 35.00905 34.93125
$out
numeric(0)
$group
numeric(0)
$names
[1] "Hommes" "Femmes"
La conclusion est qu'il n'y a pas de différence significative détectée au seuil de 5 % entre les hommes et les femmes pour la variable AGE dans ce petit échantillon d'une centaine de personnes dont deux tiers de femmes et un tiers d'hommes.
Code-source php de cette page. Retour à la page principale du cours.
|
 Retour à la page principale de
(gH)
Retour à la page principale de
(gH)







