Mais vous n'y êtes pas obligé(e)s ! Soyons clair : "faire" des statistiques ne veut rien dire et en principe personne ne vous y oblige à part vous-même [sauf pour les étudiant(e)s inscrit(e)s dans les cours de statistiques !]. Pourtant, c'est une attitude scientifique, éthique et citoyenne que d'essayer d'objectiver un fonctionnement, que de quantifier ses observations, de vouloir assoir son sentiment vis à vis d'une étude, des données d'une enquête à l'aide de valeurs numériques. Ne pas réaliser une étude statistique lorsqu'on dispose de données et se contenter de ses impressions "à la volée" réalise un vague a priori aussi éloigné d'une réflexion sérieuse et profonde qu'une discussion de comptoir l'est d'une dissertation pour l'agrégation de philosophie. "Noblesse oblige" Ce proverbe s'applique aussi aux études statistiques : si on est en "baccalauréat+8", "baccalauréat+9"... et si on passe plusieurs années à travailler sur un sujet dans le cadre d'une thèse ou d'un article, on se doit, par respect pour soi-même et pour les autres, de "bien" traiter les données dont on dispose, de "bien" présenter les résultats des analyses sur les données, de "bien" rédiger les conclusions qu'elles induisent. Pallier à la faiblesse du cerveau L'esprit humain n'est pas capable de retenir plus d'une dizaine de valeurs numériques alors l'homme et la femme dans leurs "petites têtes" doivent avoir recours à des aides extérieures que sont les documents écrits. Lorsqu'on dispose de listes de chiffres, une étude statistique simple permet de résumer, d'exprimer des tendances qu'une lecture, même approfondie ne peut fournir. Que l'on soit dans les sciences "pures et dures" ou dans les sciences "molles" il faut donc se servir d'outils mécaniques pour se rappeler ce que contiennent les listes de chiffres. C'est ce que permet une utilisation "honnête" des statistiques descriptives. Un premier exemple : "le Titanic" Supposons qu'on s'intéresse aux passagers du Titanic. Voici quelques informations les concernant, qu'on lira à l'aide de leur descriptif. Même si on "décode" les modalités, c'est à dire si on lit les données sous cette forme, il est certainement difficile de répondre à des questions comme Y avait-il beaucoup d'hommes, de femmes ?   Y a t-il eu autant de survivants en première classe que dans les membres d'équipage ? Les statistiques descriptives élémentaires (ici un tri à plat, là un tri croisé) permettent de répondre numériquement et graphiquement à ces questions : oui, il y avait plus d'hommes que de femmes comme le montre le   +-------------------------------------------------+ ! ! ! Tri à plat de la variable SEXE (n=2201) ! ! ! +-------------------------------------------------+ ! ! ! ! ! Femmes Hommes Total ! ! Effectif 470 1731 2201 ! ! Fréquence (en %) 21 79 100 ! ! ! +-------------------------------------------------+   On peut le prouver par une +-------------------------------------------------------------------------------+ ! ! ! Comparaison de pourcentages ! ! ! +-------------------------------------------------------------------------------+ ! ! ! ia 470 na 2201 pa 0.214 ! ! ib 1731 nb 2201 pb 0.786 ! ! ii 2201 nn 4402 p 0.500 ! ! ! ! dp 0.57292 r2 0.00023 ! ! r 0.01507 eps 38.01194 ! ! ! ! Au seuil de 5 % soit la valeur 1.96 ! ! on peut refuser l'hypothèse que les pourcentages sont égaux. ! ! ! +-------------------------------------------------------------------------------+ et non, il n'y a pas eu indépendance entre la survie et le fait d'être en première classe ou de faire partie des membres d'équipage car comme le montre le calcul du chi2, il y a eu plus de survivants parmi les les passagers de première classe que parmi les membres d'équipage.   Abandonner l'imprécision [souvent] malhonnêtement volontaire Qui veut noyer son chien l'accuse de la rage. En sciences, même "humaine", même "molle", même "pure et dure" il est facile de dire, de publier n'importe quoi. Il suffit de simplifier, résumer, masquer et de s'arranger comme en statistique publicitairement mercantile où on se contente de faire croire qu'il y a de la vraie science en affichant haut et fort 82.5 % des femmes ont élu le produit X comme produit de l'année sans indiquer la taille de la population (souvent une cinquantaine de "bonnes femmes", ce qui n'est ni représentatif ni significatif), le protocole d'enquête, le mode de calcul (avec ou sans non-réponses), la liste des modalités, le mode d'élection... Un deuxième exemple : la "mobilité résidentielle" Didier BESINGRAND a traité dans sa thèse (2006) de la mobilité résidentielle des séniors (55-70 ans) sur la facade atlantique française. Afin d'approfondir les raisons de localisation de ces derniers dans les espaces de réception, il a mis en place et diffusé un questionnaire qu'il a traité avec des statistiques classiques (tris à plat, tris croisés) puis en analyse des données (AFC, CAH...). Il a obtenu aux environs de 200 réponses pour 124 modalités. Avec autant de lignes et de colonnes, il est clair qu'il faut passer par un logiciel de statistiques pour y voir quelquechose et surtout pour en dire quelquechose. Dans la même étude concernant le choix des espaces d'études, il a réussi à cartographier le premier axe de l'ACP des 5 indicateurs classiques INSEE (taux d'évolution du solde migratoire, taux d'évolution des 55-70 ans, taux d'évolution du nombre de résidences secondaires, taux d'évolution du nombre de logements vacants et taux d'évolution du nombre total de logements) soit un trés grand tableau de données. L'AFC a permis de traiter en profondeur les liaisons entre lignes, entre colonnes, d'éviter de rester à la surface des phénomènes et de proposer des indicateurs numériques qui une fois interprétés fournissent une typologie des seniors sur l'ensemble de l'espace d'études, typologie que seul un humain est capable de qualifier, de rédiger. Car ne l'oublions pas, les résultats numériques issus des analyses fournissent une base de travail que le chercheur exploite en fonction de son expérience, de ses observations et de sa culture. 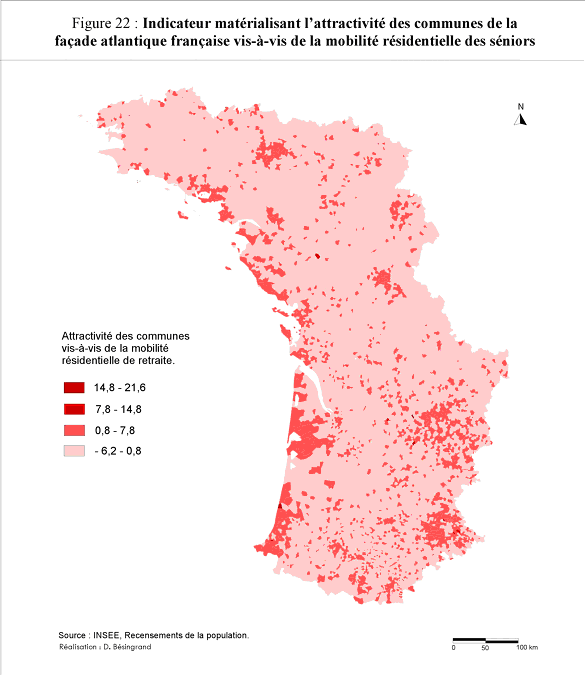Ainsi les géographes tracent des cartes qui mettent en évidence les résultats statistiques comme cellle de l'étude citée : Attention, quand même Etre en thèse, ou disposer d'un poste de MCF ou de PR ne garantit en rien l'exactitude des propos formulés. Fournir des données avec des calculs reproductibles permet de valider des contenus, sous réserve que les protocoles soient décrits et justifiés, que les résultats d'analyse soient suffisamment objectifs. Réaliser une analyse statistique ne prouve pas qu'on a bien fait : on peut avoir oublié des variables, des données, on peut avoir biaisé la population, il est possible de ne présenter que les calculs qui "arrangent" etc. Mais mettre à disposition des données, effectuer une analyse exhaustive est le début d'un gage de sérieux, d'une volonté de "faire de la science"... Intuition contre test statistique Les test statistiques vont parfois contre l'intuition, c'est pourquoi il faut être prudent quand on croit "voir des choses". Prenons une question "presque" anodine :   Si on a 45 % d'hommes et 55 % de femmes, y a-t-il une différence significative entre le pourcentages d'hommes et de femmes ?   Intuitivement, on a envie de répondre "non" ou "il n'y a pas beaucoup de différence". Le test statistique nommé "comparaison de pourcentages", si ses conditions d'application sont respectées, fournit une réponse contre-intuitive car il utilise le nombre total de personnes (qui ne figure pas explicitement dans la question). Ainsi avec 100 personnes dont 45 hommes et 55 femmes, au seuil de 5 % on peut accepter l'hypothèse que les pourcentages sont égaux. Par contre si on multiplie les effectifs par 10 (ce qui ne change rien aux pourcentages), c'est à dire pour 1000 personnes dont 450 hommes et 550 femmes, au seuil de 5 % on ne peut pas accepter cette hypothèse car 10 % de différence, cela n'est pas la même chose quand on a 100 personnes ou 1000 personnes... ce qu'on peut vérifier à l'aide de calculs simples si on connait les formules de comparaisons ou si on a une page Web pour faire les calculs... La même remarque s'applique aux comparaisons de moyenne : statistiquement, il n'y pas de différence significative au seuil de 5 % pour deux séries de 20 valeurs si la moyenne est 4.8 avec une variance de 1.1 pour la série 1 et si la moyenne est 5.4 avec une variance de 1.5 pour la série 2 alors que la différence est significative au seuil de 5 % si ces résultats sont obtenues pour 50 valeurs. Le détail des calculs se lit ici et les formules là mais vous pouvez le vérifier ici...

 

    retour à statgen (gH)