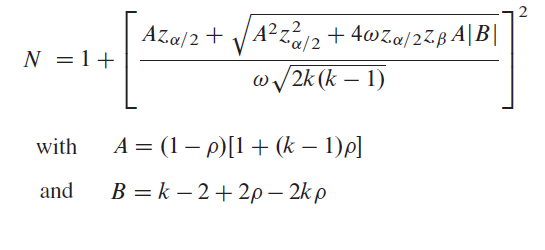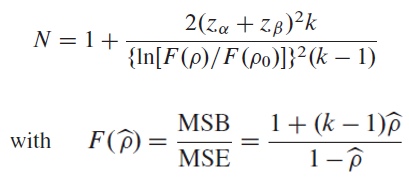Calculs de tailles d'échantillons gilles.hunault "at" univ-angers.fr   On pourra consulter notre page sampsizes pour des références Web sur le détail des calculs. Les calculs effectués sur un échantillon fournissent des valeurs nommées statistiques qui permettent d'obtenir une estimation des vraies valeurs pour la population sous-jacente, nommées paramètres. Lorsque l'estimation renvoie une seule valeur, on parle d'estimation ponctuelle ; sinon, la plage de valeurs de l'estimation par intervalle est nommée intervalle de confiance (voir la page estimations pour des exemples d'estimation). Les calculs d'estimation utilisent la taille n de l'échantillon ; pour une précision donnée, on peut déduire des formules de l'estimation la taille minimale requise n pour une proportion, une moyenne, un écart type. Dans la littérature statistique, on trouve aussi des formules pour déterminer la plus petite taille d'échantillon pour détecter une "vraie" différence entre deux proportions, ou pour tester la valeur d'un coefficient de corrélation linéaire... Table des matières cliquable : 1. Taille d'échantillon pour estimer une proportion 2. Taille d'échantillon pour estimer une moyenne 3. Taille d'échantillon pour estimer l'intervalle de confiance     d'un coefficient de corrélation classique 4. Taille d'échantillon pour estimer l'intervalle de confiance     d'un coefficient de corrélation intraclasse 4.1 qui garantit une largeur d'intervalle donnée 4.2 qui garantit la borne inférieure de l'intervalle 1. Taille d'échantillon pour estimer une proportion   Donnez : l'estimation p-chapeau de la proportion (ou 0.5 si aucune estimation n'est connue)         la marge d'erreur souhaitée en "points" (donc entre 0 et 100)         le niveau de confiance désiré (souvent 0.05 ou 0.10)         et cliquez sur le bouton        pour obtenir la taille de l'échantillon pour estimer une proportion dans une population. Un exemple de référence est celui où p-chapeau=0.169, E=4 et α=0.05 ; zα/2 vaut alors 1.96 et la taille est alors 338 (Triola, Biostatistics for the Biological and Health Sciences, 3d ed., Pearson, p. 267). 2. Taille d'échantillon pour estimer une moyenne   Donnez : l'écart type de la population (ou une estimation de cet écart-type)         la marge d'erreur souhaitée en "points" (donc entre 0 et 100)         le niveau de confiance désiré (souvent 0.05 ou 0.10)         et cliquez sur le bouton        pour obtenir la taille de l'échantillon pour estimer une moyenne dans une population. Un exemple de référence est celui où σ=0.64, E=0.25 et α=0.05 ; zα/2 vaut alors 1.96 et la taille est alors 25 (Zar, Biostatistical Analysis, 4th ed., Prentice Hall, p. 106) ; le livre utilise le t de Student au lieu de la loi normale, d'où une taille de 27 au lieu de 25. 3. Taille d'échantillon pour estimer l'intervalle de confiance d'un coefficient de corrélation classique      (Pearson, Spearman, Kendall)   Donnez : le type de corrélation modélisée         Pearson Spearman Kendall la valeur du coefficient de corrélation ρ (rho)         la largeur de l'intervalle de confiance ω (omega)         le niveau de confiance désiré (souvent 0.05 ou 0.10) α (alpha)         et cliquez sur le bouton        pour obtenir la taille de l'échantillon pour estimer l'intervalle de confiance d'un coefficient de corrélation. Un exemple de référence est celui où pour une corrélation de Pearson, ρ=0.8, ω=0.2 et α=0.05 ; zα/2 vaut alors 1.96 et la taille est alors 56.  Voir par exemple l'article de D. G. Bonett et T. A. Wright dans Psychometrika 2000, vol. 65, no1, pp. 23-28. Merci à Sandrine BERTRAIS de m'avoir indiqué l'article et les formules correspondantes. Formule programmée : 4.1 Taille d'échantillon pour estimer l'intervalle de confiance d'un coefficient de corrélation intraclasse      qui garantit une largeur d'intervalle donnée   Donnez : la valeur du coefficient de corrélation ρ (rho)         la largeur de l'intervalle de confiance ω (omega)         le nombre d'observations k         le niveau de confiance désiré (souvent 0.05 ou 0.10) α (alpha)         la valeur de puissance désirée (souvent 0.20) β (beta)         et cliquez sur le bouton        pour obtenir la taille de l'échantillon pour estimer l'intervalle de confiance d'un coefficient de corrélation intraclasse avec une largeur d'intervalle garantie. Un exemple de référence est celui où pour une corrélation de Pearson, ρ=0.60, ω=0.10, k=3 α=0.05 et β=0.20 ; la taille d'échantillon requise est alors 114. Voir par exemple l'article de G. Y. Zou Sample size formulas for estimating intraclass correlation coefficients. Merci à Pascal VEILLON de m'avoir indiqué l'article. Formule programmée : 4.2 Taille d'échantillon pour estimer l'intervalle de confiance d'un coefficient de corrélation intraclasse      qui garantit la borne inférieure de l'intervalle   Donnez : la valeur du coefficient de corrélation ρ (rho) supposé         la valeur inférieure du coefficient de corrélation ρ0 (rho zéro) désiré         le nombre d'observations k         le niveau de confiance désiré (souvent 0.05 ou 0.10) α (alpha)         la valeur de puissance désirée (souvent 0.20) β (beta)         et cliquez sur le bouton        pour obtenir la taille de l'échantillon pour estimer l'intervalle de confiance d'un coefficient de corrélation intraclasse avec une borne inférieure d'intervalle garantie. Un exemple de référence est celui où pour une corrélation de Pearson, ρ=0.70, ρ0=0.60, k=2, α=0.05 et β=0.20  la taille d'échantillon requise est alors 205. Voir par exemple l'article de G. Y. Zou Sample size formulas for estimating intraclass correlation coefficients. Merci à Pascal VEILLON de m'avoir indiqué l'article. Formule programmée :

 

 

   Retour à la page principale de   (gH)