Statistiques inférentielles, notions essentielles gilles.hunault "at" univ-angers.fr   Table des matières cliquable   1. Qu'est-ce qu'un intervalle de confiance ?   2. Qu'est-ce qu'un test ?   3. Données appariées ou non ? «normales» ou non ?   4. Tests paramétriques et non paramétriques   La plupart des données qu'on utilise correspondent souvent non pas à l'ensemble de la population mais juste à un échantillon. Sous réserve que certaines hypothèses soient vérifiées, les statistiques inférentielles permettent d'estimer la moyenne de la population à partir de la moyenne d'un échantillon, de savoir si deux échantillons (ou plus) peuvent être considérés comme issus d'une même population et donc de comparer leurs moyennes, leurs variances...   1. Qu'est-ce qu'un intervalle de confiance ? A partir de la moyenne et de l'écart-type des données d'un échantillon pour une variable quantitative, il est possible d'estimer la moyenne de cette variable pour la population sous-jacente et de fournir un intervalle susceptible de contenir cette valeur. Cet intervalle est nommé intervalle de confiance en français, confidence interval en anglais. De façon similaire, pour des données d'échantillon correspondant à une variable qualitative binaire, il est possible d'estimer un intervalle de confiance pour la proportion dans la population. Voir le wiki français et le wiki anglais pour savoir comment il se calcule et aussi pour constater la différence entre ces deux wikis. De plus, notre page estimation permet de calculer rapidement ces intervalles. 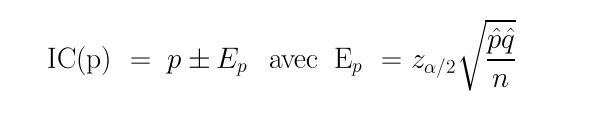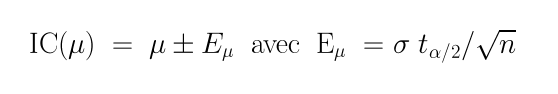Voici les formules associées qu'il est bon de connaitre afin de comprendre ce que font les fonctions R qui calculent ces intervalles :       Pour calculer un intervalle de confiance, il faut utiliser un niveau de confiance, qui vaut par défaut 0,95 ce qui signifie qu'on a confiance à 95 % dans cet intervalle (et surtout pas, stricto sensu que la probabilité de contenir la moyenne de la population dans cet intervalle est de 0,95). On laisse le le lecteur expérimenter le sens de variation de la largeur de l'intervalle en fonction de ce niveau de confiance, utilisable via le paramètre conf.level dans la fonction t.test de R. R ne propose aucune fonction dédiée pour calculer l'intervalle de confiance d'une moyenne. Toutefois, la fonction t.test fournit cet intervalle de confiance en plus de réaliser le test. Comme cette fonction renvoie une liste de résultats, on accède à l'intervalle par son nom conf.int précédé du symbole dollar $ : Code-source R (données cps2.dar) :       # intervalle de confiance du salaire horaire pour les données CPS2            cps2 <- read.table("cps2.dar",head=TRUE,row.names=1)      cat("Données CPS2 ",nrow(cps2)," lignes et ",ncol(cps2)," colonnes.\n")            ttsa <- t.test(cps2$salhor)      icsa <- ttsa$conf.int      alph <- attr(icsa,"conf.level")            cat("IC du salaire horaire : ",icsa," $, niveau ",alph,"\n")      cat("IC à 99 % : ",t.test(cps2$salhor,conf.level=0.99)$conf.int,"$\n")                  Résultats :       Données CPS2 1000 lignes et 10 colonnes.      IC du salaire horaire : 9.825387 10.60065 $, niveau 0.95      IC à 99 % : 9.703227 10.72281 $                  On peut utiliser les mêmes formules pour calculer la taille de l'échantillon à analyser lorsqu'on veut obtenir une moyenne, un coefficient de corrélation avec une précision donnée. Voir par exemple notre page taillechant pour de tels calculs. Si on veut utiliser, statgh.r les fonctions sont nommées ic() pour l'aide générale, icm(), icmQT(), icp() etc. pour une moyenne, une proportion... Code-source R :       # fonctions gh pour intervalles de confiance            ic()            # intervalle de confiance du salaire horaire pour les données CPS2            cps2 <- lit.dar("cps2.dar")      cat("Données CPS2 ",nrow(cps2)," lignes et ",ncol(cps2)," colonnes.\n")      attach(cps2)            icmQT(salhor,0.95,TRUE)            cat("IC à 99 % : ",icmQT(cps2$salhor,0.99),"$\n")            detach(cps2)                  Résultats :       Vous disposez de cinq fonctions pour les intervalles de confiance      et de deux fonctions pour les calculs de taille d'échantillons :            icp      pour l'estimation par intervalle d'une proportion      syntaxe : icp(nbVal,pChap,nivConf=0.05,echo=FALSE)            icm      pour l'estimation par intervalle d'une moyenne sachant m et s      syntaxe : icm(nbVal,moyQt,ectQt,nivConf=0.05,affichage=FALSE)            icmQT      pour l'estimation par intervalle de la moyenne d'une QT      syntaxe : icmQT(varQT,nivConf=0.05,affichage=FALSE)      (on peut aussi utiliser t.test(varQT)            ice      pour l'estimation par intervalle de l'écart-type      syntaxe : ics(nbVal,ectQt,nivConf=0.05,echo=FALSE)            iceQT      pour l'estimation par intervalle d'une écart-type d'une QT      syntaxe : icsQT(varQT,nivConf=0.05,echo=FALSE)            tailleEchProp      pour la taille d'un échantillon en vue d'estimer une proportion      syntaxe : tailleEchProp(pChapeau,margeErreur,nivConf=0.05)                  tailleEchMoy      pour la taille d'un échantillon en vue d'estimer une moyenne      syntaxe : tailleEchMoy(ecartType,margeErreur,nivConf=0.05)            Données CPS2 1000 lignes et 10 colonnes.      Pour 1000 valeurs de moyenne 10.21302 et d'écart-type 6.24664 au niveau 0.95      la valeur critique issue de la loi du t de Student pour 999 ddl est 0.06272253 soit 0.063      l'intervalle de confiance est donc sans doute [ 10.20063 ; 10.22541 ]      soit, en arrondi, [ 10.201 ; 10.225 ]      IC à 99 % : 10.21054 10.21550 $                        On pourra consulter avec profit le code-source des fonctions icm() et icmQT() ci-dessous : ########################################### icm <- function(nbVal,moyQt,ectQt,nivConf=0.05,affichage=FALSE) { ########################################### if (missing(nbVal)) { cat("icm : intervalle de confiance d'une moyenne \n") ; cat("syntaxe : icm(nbVal,moyQt,ectQt,nivConf=0.05,echo=FALSE) \n") cat("exemples : icm(50,25.03,1.341641) \n") cat(" icm(50,25.03,1.341641,0.01) \n") cat(" icm(50,25.03,1.341641,0.01,TRUE) \n") return() ; } ; # fin de si ddl <- nbVal-1; alp <- nivConf/2; valt <- qt(alp,ddl,lower.tail=FALSE) f_t <- sprintf("%6.3f",valt) ; margeE <- valt*ectQt/sqrt(nbVal) liminf <- moyQt - margeE limsup <- moyQt + margeE if (affichage) { cat(" Pour ",nbVal," valeurs de moyenne ",moyQt," et d'écart-type ",ectQt," au niveau ",nivConf,"\n") cat(" la valeur critique issue de la loi du t de Student pour ",ddl," ddl est ",valt," soit ",f_t,"\n") cat(" l'intervalle de confiance est donc sans doute [",liminf," ; ",limsup," ]\n ") cat(" soit, en arrondi, [ ",sprintf("%0.3f",liminf)," ; ",sprintf("%0.3f",limsup)," ]\n ") } # fin de si return(c(liminf,limsup)) } ; # fin de fonction icm ########################################### icmQT <- function(varQT,nivConf=0.05,affichage=FALSE) { ########################################### if (missing(varQT)) { cat("icmQT : intervalle de confiance d'une moyenne sachant ses valeurs\n") ; cat("syntaxe : icmQT(varQT,nivConf=0.05,echo=FALSE) \n") cat("exemples : icm(lng) \n") cat(" icm(AGE_ELF,0.01) \n") return() ; } ; # fin de si n <- length(varQT) m <- mean(varQT) s <- sd(varQT) return( icm(n,m,s,nivConf,affichage) ) } ; # fin de fonction icmQT ########################################### 2. Qu'est-ce qu'un test ? Un test statistique [d'hypothèse] est une procédure statistique rigoureuse qui établit si une hypothèse liée à une population peut être refusée ou non, au vu de données d'échantillon(s). Elle se déroule en 4 étapes : On commence par établir clairement l'hypothèse-métier à tester et on en déduit les hypothèses statistiques H0 et H1 correspondantes, nommées respectivement hypothèse nulle et hypothèse alternative. Suivant l'hypothèse alternative (comme μ≠μ0 ou μ>μ0), le test est bilatéral ou unilatéral (one sided ou two sided en anglais). On choisit ensuite une statistique de test pour modéliser la loi théorique de la variable aléatoire lorsque l'hypothèse nulle est vérifiée et un niveau de confiance ou, ce qui revient au même, un risque de première espèce α. On peut alors calculer un intervalle de confiance tel que les valeurs de la statistique de test appartiennent à l'intervalle avec la probabilité 1-α. On dispose alors d'un domaine d'acceptation (l'intervalle obtenu) et d'un domaine de refus (les autres valeurs). Le choix de la valeur α n'est donc pas anodin et il doit être effectué avant de réaliser le test. Compte-tenu de ce qui a été dit dans le paragraphe précédent, α est le risque de refuser à tort H0 («à tort» sous-entend qu'on parie sur le fait H0 doit être vraie), nommé aussi degré de significativité, incorrectement car en «français pur et dur» il serait plus juste de parler de degré de signification. La valeur de α doit correspondre à la largeur de l'intervalle. Il faut donc la diviser par deux en cas de test bilatéral pour connaitre la probabilité de dépasser la valeur : On calcule alors la valeur de la statistique de test pour les données (nommée statistique d'écart) et on compare cette valeur aux valeurs théoriques, ce qui passe par le calcul de la probabilité de dépasser la valeur de la statistique de test au seuil α considéré, nommée internationalement petit-pé ou p-value ou, en «français rigoureux» probabilité critique. On conclut alors statistiquement en utilisant éventuellement le degré de significativité α et on conclut ensuite en termes-métier. On a le choix entre : comparer la statistique d'écart des données avec celle théorique au seuil choisi ; calculer la p-value de dépasser la statistique d'écart ; regarder si la valeur proposée est dans ou en dehors de l'intervalle de confiance du paramètre estimé. Voici un exemple de test de conformité, adapté de la section 3 du chapitre 7 du cours de D. Mouchiroud à Lyon : Le prix d'une tasse de café en 2004 était environ de 1 euro pour la France, soit moyenne de μ=1 euro et un écart-type de σ=0,1 euro. Une petite chaine de brasseries fait payer en moyenne m=1,12 euros le café pour ses n=9 brasseries. Ce prix est-il conforme à l'ensemble des prix du marché ? Détaillons le test : L'hypothèse-métier à tester est : la moyenne du café pour (m) les brasseries des chaines est-elle égale à celle de l'ensemble des prix en France (m0) ? On en déduit les hypothèses statistiques H0 : μ=μ0 et H1 μ≠μ0 où μ est la moyenne de la population d'où m est extraite. On choisit comme statistique S de test l'écart X - μ0 où X suit une loi normale de paramètre moy=μ0 et ect =√(σ²/n). S est donc modélisée par une loi normale de moyenne 0 et de variance σ²/n. On prend pour α la valeur 0,05 («comme d'habitude»). La valeur de la statistique de test pour nos données vaut 3,6 et la valeur théorique de la probabilité critique ou p-value est 1,96 (via α=0,05). Comme 3,6 dépasse 1,96, on peut refuser l'hypothèse nulle. On peut aussi calculer la p-value de dépasser 3,6 ; on trouve 0,0003 qui est inférieur à α donc là encore, on peut refuser H0. Enfin, l'intervalle de confiance de S est [ 0,92 ; 1,08 ]. Il ne contient pas la valeur zéro donc on refuse H0. Statistiquement, on est droit de rejeter H0 au seuil de 5 % ; en termes-métier, on dira que l'échantillon des 9 brasseries est significativement différent de l'ensemble des établissements au niveau du prix du café, donc que ce prix dans les brasseries n'est pas conforme à l'ensemble des prix du marché français (au seuil de 5 %). Voici le code-source R des calculs :       # valeur théorique de la probabilité critique            alpha <- 0.05      eseuil <- qnorm(1-alpha/2) # test bilatéral            # valeur de la statistique de test pour les données            n <- 9      sigma <- 0.1      m <- 1.12      m0 <- 1            st <- abs(m-m0)/sqrt( (sigma**2)/ n)            # probabilité critique liée aux données            pc <- dnorm(st)/2 # test bilatéral            # intervalle de confiance de m            icprix <- icm(n,m0,sigma)      icinf <- icprix[1]      icsup <- icprix[2]            # affichages            cat("\n")            cat("Statistique d'écart : ",st," probabilité critique théorique : ",round(eseuil,2)," pour alpha=",alpha,"\n")      if (st>eseuil) {      cat("Il faut rejeter l'hypothèse nulle.\n")      } else {      cat("On ne peut pas rejeter l'hypothèse nulle.\n")      } ; # fin de si            cat("\n")            cat("Probabilité critique des données : ",sprintf("%0.4f",pc),"\n")      if (pc<alpha) {      cat("Il faut rejeter l'hypothèse nulle.\n")      } else {      cat("On ne peut pas rejeter l'hypothèse nulle.\n")      } ; # fin de si            cat("\n")            cat("Intervalle de confiance de la moyenne : [ ",icinf, " , ",icsup," ]\n")      if ((m<=icinf) | (m>=icsup)) {      cat("Il faut rejeter l'hypothèse nulle.\n")      } else {      cat("On ne peut pas rejeter l'hypothèse nulle.\n")      } ; # fin de si            cat("\n")                  Et leurs résultats :       Statistique d'écart : 3.6 probabilité critique théorique : 1.96 pour alpha= 0.05      Il faut rejeter l'hypothèse nulle.            Probabilité critique des données : 0.0003      Il faut rejeter l'hypothèse nulle.            Intervalle de confiance de la moyenne : [ 0.9231332 , 1.076867 ]      Il faut rejeter l'hypothèse nulle.                  Nous laissons au lecteur le soin de trouver comment obtenir rapidement ces résultats avec la fonction t.test() de R. 3. Données appariées ou non ? «normales» ou non ? Comme leur nom l'indique, les données appariées sont liées par paires. Par exemple une valeur biologique avant et après un traitement médical induit des données appariées, comme le sont des prix d'un même produit pour deux années consécutives. Souvent en R il faut ajouter paired=TRUE au test utilisé pour indiquer que les données sont appariées. Il est important de savoir si les données sont appariées car il faut en tenir compte pour la statistique de test : on s'attend tout naturellement à ce que des données appariées soient plus proches entre elles que des données «quelconques» et donc les résultats du test sont plus exigeants qu'avec des données non appariées. La notion de données appariées est un réalité qu'on doit indiquer si on le sait. Il n'y a pas de test pour savoir si les données le sont ou pas. Contrairement au concept de normalité qui peut se tester. On dit que des données sont «normales» par abus de langage pour dire qu'elles suivent une distribution normale (ou une distribution de loi normale). Le fait qu'elles correspondent à une loi normale signifie que la normalité (ou plutôt que la condition de normalité) est respectée. Certains tests requiérent cette normalité comme condition de validité. En d'autres termes, on n'a pas le droit d'appliquer un test qui exige la normalité comme pré-requis si cette condition n'est pas vérifiée. Pour savoir si des données suivent une loi normale, il faut bien sûr utiliser des tests de normalité... Remarque importante : en cas de doute, il vaut mieux utiliser un test non paramétrique lorsqu'on suspecte une non normalité des données. Lorsqu'on calcule l'intervalle de confiance d'une moyenne, c'est la normalité de l'estimateur de la moyenne qui doit être prise en compte. Si le nombre de valeurs est supérieur à 50, la normalité peut être tenue pour acquise. Dans le cas contraire, il faut tester la normalité des données de l'échantillon, par exemple à l'aide du test de Shapiro-Wilk, via la fonction shapiro.test après avoir regardé la symétrie et la distribution des données via un histogramme des classes. 4. Tests paramétriques et non paramétriques Comme indiqué dans la section 2, la statistique de test résulte d'un choix. Le modèle théorique sous-jacent peut utiliser ou non une loi paramétrée, par exemple la loi normale centrée réduite, une loi de Poisson de paramètre λ... Le choix de tels modèles est lié à des conditions de validité, par exemple de normalité de l'estimateur utilisé ou de normalité des données de l'échantillon (ce qui n'est pas la même chose). Lorsque les données ne suivent pas ces hypothèses de validité, le test choisi est invalide et il faut en choisir un autre. Quand un test met en jeu une loi théorique avec une distribution paramétrée, on dit que le test est paramétrique, ou plus exactement contraint par une distribution paramétrée. Dans le cas contraire, on parle de test non paramétrique (ou plutôt de test libre de distribution paramétrée). Un test paramétrique est en général plus puissant qu'un test non paramétrique, c'est-à-dire qu'il permet de détecter plus finement des différences significatives pour un même échantillon. De la même façon, pour un niveau α donné, il faut utiliser plus de données avec un test non paramétrique pour obtenir les mêmes résultats qu'avec un test paramétrique. Par contre, comme souvent un test paramétrique met en jeu de conditions de validité, il n'est pas toujours possible de l'utiliser. Chaque test paramétrique a donc son test non paramétrique associé. Voir notre liste de tests pour savoir lequel utiliser. 4.1 Comparaison de deux moyennes Dans le dossier VINS les pays CANADA et SUISSE semblent avoir des moyennes proches (respectivement 2,81 et 2,96 hhl.) Peut-on considérer que les moyennes sont égales ? Si on fonce tête baissée, on peut être tenté d'utiliser le test t de Student pour effectuer la comparaison :       # comparaison "stupide" de SUISSE et CANADA dans le dossier VINS            vins <- lit.dar("vins.dar")      cat("Données VINS ",nrow(vins)," lignes et ",ncol(vins)," colonnes.\n")            # test t de Student standard : var.equal=TRUE            print( t.test(vins$SUISSE, vins$CANADA,var.equal=TRUE) )            # test t de Student adapté = test de Welch            print( t.test(vins$SUISSE, vins$CANADA,var.equal=FALSE) )                  On en déduirait alors qu'il n'y a pas de différence significative au seuil de 5 % à l'aide du test de Welch (soit parce que la p-value est supérieure à 0,05 soit parce que l'intervalle de confiance contient zéro). Le test de Welch, en réponse à une demande de test t de Student, en est une variante adaptée au cas de variances inégales :       Données VINS 18 lignes et 8 colonnes.            Two Sample t-test            data: vins$SUISSE and vins$CANADA      t = 0.0624, df = 34, p-value = 0.9506      alternative hypothesis: true difference in means is not equal to 0      95 percent confidence interval:      -4.768079 5.070301      sample estimates:      mean of x mean of y      2.964611 2.813500                  Welch Two Sample t-test            data: vins$SUISSE and vins$CANADA      t = 0.0624, df = 26.732, p-value = 0.9507      alternative hypothesis: true difference in means is not equal to 0      95 percent confidence interval:      -4.817816 5.120038      sample estimates:      mean of x mean of y      2.964611 2.813500                  Malheureusement, nous avions indiqué que les tests utilisent des conditions d'application. Pour un test t, il faut un nombre suffisant de données (plus de 50, or ici n=18) ou la normalité des données. De plus, il faut préciser si on peut considérer les variances comme égales ou inégales. Regardons ce que cela donne ici :       # lecture des données            vins <- lit.dar("vins.dar")      cat("Données VINS ",nrow(vins)," lignes et ",ncol(vins)," colonnes.\n")      suisse <- vins$SUISSE      canada <- vins$CANADA            # test de la normalité de la variable SUISSE            decritQT("SUISSE",suisse,"hhl",TRUE,"c4suisse.png")      print( shapiro.test(suisse) )            # test de la normalité de la variable CANADA            decritQT("CANADA",canada,"hhl",TRUE,"c4canada.png")      print( shapiro.test(canada) )            # test de l'égalité des variances            print( var.test(suisse,canada))                              Données VINS 18 lignes et 8 colonnes.            DESCRIPTION STATISTIQUE DE LA VARIABLE SUISSE            Taille 18 individus      Moyenne 2.9646 hhl      Ecart-type 4.8821 hhl      Coef. de variation 165 %      1er Quartile 0.1197 hhl      Mediane 0.5355 hhl      3eme Quartile 2.713 hhl      iqr absolu 2.593 hhl      iqr relatif 484 %      Minimum 0.0000 hhl      Maximum 17.3270 hhl            Tracé tige et feuilles            The decimal point is 1 digit(s) to the right of the |            0 | 00000000011113      0 | 7      1 | 02      1 | 7                  vous pouvez utiliser c4suisse.png                  Shapiro-Wilk normality test            data: suisse      W = 0.6542, p-value = 2.455e-05                  DESCRIPTION STATISTIQUE DE LA VARIABLE CANADA            Taille 18 individus      Moyenne 2.8135 hhl      Ecart-type 8.7046 hhl      Coef. de variation 309 %      1er Quartile 0.071 hhl      Mediane 0.2855 hhl      3eme Quartile 1.127 hhl      iqr absolu 1.056 hhl      iqr relatif 370 %      Minimum 0.0000 hhl      Maximum 38.5030 hhl            Tracé tige et feuilles            The decimal point is 1 digit(s) to the right of the |            0 | 00000000000111223      1 |      2 |      3 | 9                  vous pouvez utiliser c4canada.png                  Shapiro-Wilk normality test            data: canada      W = 0.3297, p-value = 3.629e-08                  F test to compare two variances            data: suisse and canada      F = 0.3146, num df = 17, denom df = 17, p-value = 0.02205      alternative hypothesis: true ratio of variances is not equal to 1      95 percent confidence interval:      0.1176712 0.8409412      sample estimates:      ratio of variances      0.3145704                  Il n'y a clairement ni normalité, ni égalité des variances. Donc le test paramétrique du t de Student ou le test paramétrique de Welch ne doit pas être utilisé. Le test non paramétrique correspondant est le test de Wilcoxon, Mann et Whitney qui vient tester les rangs des données et non les données elles-mêmes. Le graphique associé est celui des boxplots cote à cote, avec éventuellement des encoches :       # boites à moustache pour comparer non paramétriquement SUISSE et CANADA            vins <- lit.dar("vins.dar")      suisse <- vins$SUISSE      canada <- vins$CANADA            qt <- c(suisse,canada)      ql <- c( rep("SUISSE",length(suisse)),rep("CANADA",length(canada)) )      titre <- "CANADA vs SUISSE (dossier VINS)"            gr("c4boxp1.png")      boxplot(qt~ql,main=titre,col="yellow",pch=21,bg="red",notch=FALSE)      dev.off()            gr("c4boxp2.png")      boxplot(qt~ql,main=titre,col="yellow",pch=21,bg="red",notch=TRUE)      dev.off()            Les fonctions de statgh.r permettent bien sûr d'obtenir rapidement tout cela, et plus encore :       # description de SUISSE et CANADA conjointement            vins <- lit.dar("vins.dar")      suisse <- vins$SUISSE      canada <- vins$CANADA            qt <- c(suisse,canada)      qlnum <- c( rep(1,length(suisse)),rep(2,length(canada)) )            decritQTparFacteur("VINS ",qt,"hhl"," SUISSE vs CANADA ",qlnum,c("SUISSE","CANADA"),TRUE,"c4qtql1.png")      compare2QT("CANADA vs SUISSE (dossier VINS)","CANADA",canada,"SUISSE",suisse,"hhl",TRUE,"c4qtql2.png")                        VARIABLE QT VINS ,unit=hhl      VARIABLE QL SUISSE vs CANADA labels : SUISSE CANADA            N Moy Unite Ect Cdv Q1 Med Q3 EIQ Min Max      Global 36 2.8891 hhl 7.0575 244 0.09675 0.436 1.409 1.312 0 38.503      SUISSE 18 2.9646 hhl 4.8821 165 0.1197 0.5355 2.713 2.593 0 17.327      CANADA 18 2.8135 hhl 8.7046 309 0.071 0.2855 1.127 1.056 0 38.503            vous pouvez utiliser c4qtql1.png      Analysis of Variance Table            Response: nomVarQT      Df Sum Sq Mean Sq F value Pr(>F)      nomVarQL 1 0.21 0.206 0.0039 0.9506      Residuals 34 1792.90 52.732            Shapiro-Wilk normality test            data: varQt1      W = 0.3297, p-value = 3.629e-08                  Shapiro-Wilk normality test            data: varQt2      W = 0.6542, p-value = 2.455e-05                  F test to compare two variances            data: varQt1 and varQt2      F = 3.1789, num df = 17, denom df = 17, p-value = 0.02205      alternative hypothesis: true ratio of variances is not equal to 1      95 percent confidence interval:      1.189144 8.498257      sample estimates:      ratio of variances      3.178938                  Welch Two Sample t-test            data: varQt1 and varQt2      t = -0.0624, df = 26.732, p-value = 0.9507      alternative hypothesis: true difference in means is not equal to 0      95 percent confidence interval:      -5.120038 4.817816      sample estimates:      mean of x mean of y      2.813500 2.964611                  Wilcoxon rank sum test with continuity correction            data: varQt1 and varQt2      W = 146, p-value = 0.6238      alternative hypothesis: true location shift is not equal to 0                  VARIABLE QT CANADA vs SUISSE (dossier VINS) unité : hhl      VARIABLE QL Groupes labels : CANADA SUISSE            N Moy Unite Ect Cdv Q1 Med Q3 EIQ Min Max      Global 36 2.8891 hhl 7.0575 244 0.09675 0.436 1.409 1.312 0 38.503      CANADA 18 2.8135 hhl 8.7046 309 0.071 0.2855 1.127 1.056 0 38.503      SUISSE 18 2.9646 hhl 4.8821 165 0.1197 0.5355 2.713 2.593 0 17.327      Analysis of Variance Table            Response: nomVarQT      Df Sum Sq Mean Sq F value Pr(>F)      as.factor(nomVarQL) 1 0.21 0.206 0.0039 0.9506      Residuals 34 1792.90 52.732            4.2 Intervalle de confiance et «nombre de sujets nécessaires» dans l'estimation d'une proportion Avec un peu d'attention, il est clair que la formule qui calcule un intervalle de confiance, comme celle pour une proportion, soit : 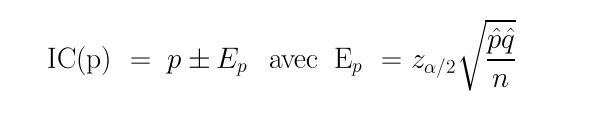peut être «retournée» afin de déduire n si on se donne la précision Ep, soit :       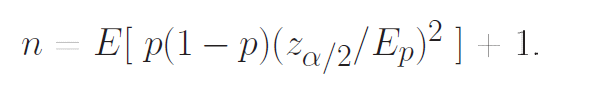On consultera donc en synoptique nos pages estimations et tailles d'échantillons pour comprendre les liens en général entre le calcul des intervalles de confiance et celui des tailles d'échantillons. 4.3 Comparaison d'effectifs Le test du χ² (ki-deux) est un test non paramétrique qui s'applique à de nombreuses situations : comparaison d'effectifs observés et théoriques (χ² d'adéquation), analyse du tri croisé de deux variables qualitatives (χ² d'indépendance)...La fonction R qui l'implémente se nomme chisq.test. Vous trouverez sur la page chideux.htm un exemple de calcul de χ² détaillé. Par exemple, pour un χ² d'adéquation (copie locale) entre des données observées Oi et des effectifs théoriques Ti, la valeur du de la statistique de test est une simple somme pondérée de carrés de différences. La loi théorique sous-jacente est donc une somme de carrés de lois normales indépendantes, c'est-à-dire justement la loi du χ² !   retour au plan de cours

 

 

   Retour à la page principale de   (gH)