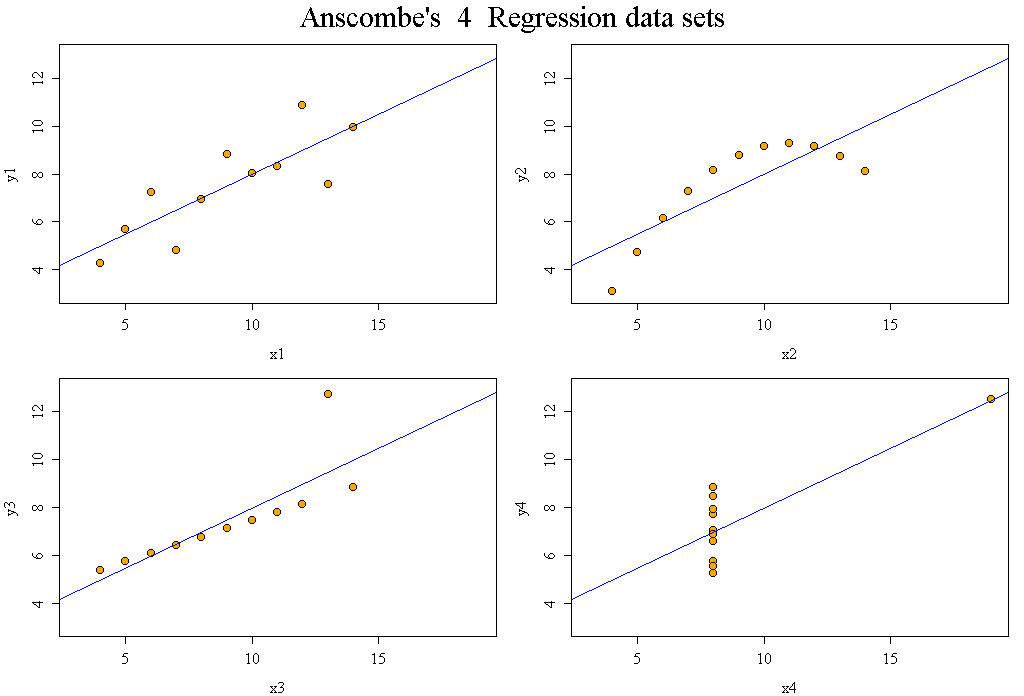1. Rappels sur les indicateurs (moyenne, médiane...) et leur usage
Pour calculer la moyenne d'une série de valeurs en R, on utilise la fonction mean() et pour en calculer la médiane, la fonction median(). Quelle est la différence statistique entre ces deux indicateurs-résumés ? Pourquoi calcule-t-on en général pour des humains la moyenne de la taille et la médiane des poids ? Pourquoi le minimum et le maximum ne sont-ils pas considérés comme des «bons» indicateurs statistiques ?
Comment faire s'il y a des valeurs NA dans les données ?
On pourra utiliser comme jeu d'essai le vecteur défini par v <- c(5,1:8,2,NA,30:50,5) avant d'effectuer ces calculs sur des données plus importantes comme la longueur en résidus (acides aminés) des protéines du dossier LEA.
Y a-t-il des représentations graphiques associées ?
Moyenne et médiane sont des indicateurs-résumés de tendance centrale (ou "centre"). La moyenne est sensible aux valeurs extrêmes, pas la médiane. Par exemple, une moyenne de salaires est "biaisée" s'il y a un très gros salaire. Il est conseillé d'utiliser la médiane dès lors que le rapport maximum/minimum dépasse 2 ou 3 et surtout s'il y a un changement d'orde de grandeur. Il est possible de trouver quelqu'un qui fait deux fois votre poids (même si c'est peut être rare), mais personne ne fait deux fois votre taille, ce qui explique la moyenne de la taille et la médiane des poids.
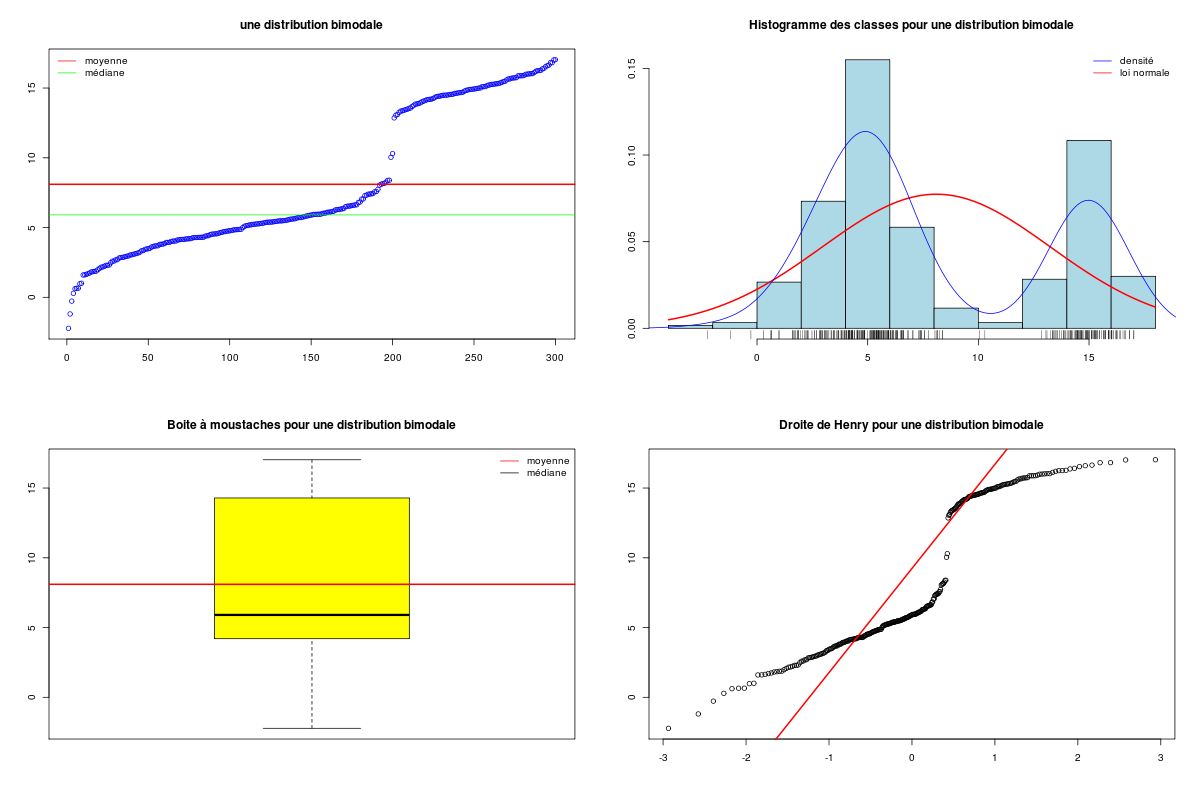
De toutes façons, moyenne et médiane sont inadaptées dès que la distribution n'est pas unimodale, comme on peut le voir ci-dessous.
# une distribution bi-modale
y1 <- rnorm(n=200,mean=5,sd=2)
y2 <- rnorm(n=100,mean=15,sd=1)
ybi <- c(y1,y2)
hist(ybi)
# description de y
print( summary(ybi) )
print( fivenum(ybi) )
# fonction (gH)
decritQT("une distribution bimodale",ybi,"",TRUE,"bimodal1.png")
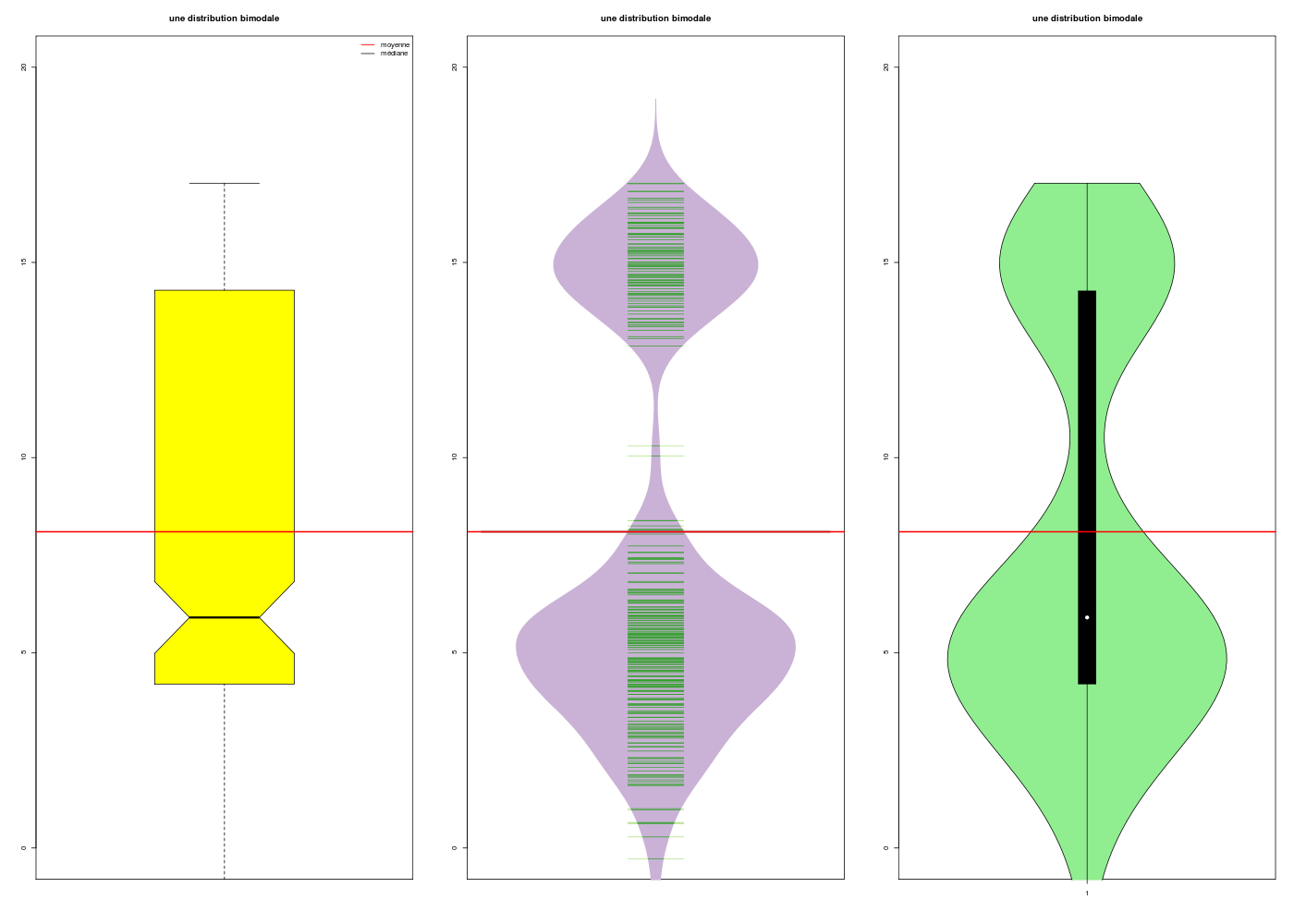
# boxplot, beanplot et violinplot à la rescousse
gr("bimodal2.png") ;
par(mfrow=c(1,3))
limy <- c(0,20)
boxplotQT("une distribution bimodale",ybi,ylim=limy,notch=TRUE)
beanplotQT("une distribution bimodale",ybi,ylim=limy)
violinplotQT("une distribution bimodale",ybi,ylim=limy)
dev.off()
Min. 1st Qu. Median Mean 3rd Qu. Max.
-1.883 4.357 6.378 8.310 14.320 18.000
[1] -1.882926 4.347843 6.378132 14.329484 18.001344
DESCRIPTION STATISTIQUE DE LA VARIABLE une distribution bimodale
Taille 300 individus
Moyenne 8.3096
Ecart-type 5.0428
Coef. de variation 61 %
1er Quartile 4.3566
Mediane 6.3781
3eme Quartile 14.3231
iqr absolu 9.9665
iqr relatif 156.0000 %
Minimum -2
Maximum 18
Tracé tige et feuilles
The decimal point is at the |
-1 | 9
-0 | 0
0 | 2459
1 | 34466799
2 | 01112344457999
3 | 011122233333444445555666668888888
4 | 0001111233333344445555555666667788888999999
5 | 0011111122234444466667778899999999
6 | 111112223334444556668999999
7 | 011122223334445667
8 | 00122233367799
9 | 0
10 | 05
11 |
12 |
13 | 001114566677888
14 | 0122222333334444555566667777777788999
15 | 00011112233333345566778889999
16 | 00011112244467789
17 | 4
18 | 0
Le minimum et le maximum ne sont pas robustes car ils ne représent que peu d'individus au sens statistique du terme. Ce ne sont donc pas des bons résumés de l'ensemble des valeurs et une seule valeur très élevée ou très faible faussera la moyenne (donc l'écart-type). C'est pourquoi on a parfois recours à la moyenne tronquée obtenue sous R avec le paramètre trim.
S'il y a des valeurs manquantes, on doit utiliser le paramètre na.rm=TRUE, car sinon moyenne et médianes valent aussi NA. Pour enlever les valeurs manquantes, on peut utiliser na.omit().
v <- c(5,1:8,2,NA,30:50,5)
cat("pour ",length(v)," valeurs.\n")
cat("Moyenne ratée : ",mean(v)," " )
cat("médiane ratée : ",median(v) )
cat("\n")
cat("Moyenne réussie : ",mean(v,na.rm=TRUE), " " )
cat("médiane réussie : ",median(v,na.rm=TRUE) )
cat("\n")
vv <- na.omit(v)
cat("\n")
cat("moyenne ",mean(vv)," " )
cat("médiane ",median(vv)," " )
cat("pour ",length(vv)," valeurs.\n")
pour 33 valeurs.
Moyenne ratée : NA médiane ratée : NA
Moyenne réussie : 27.75 médiane réussie : 34.5
moyenne 27.75 médiane 34.5 pour 32 valeurs.
Si on passe maintenant aux données proposées, à savoir les longueurs en acides aminés des protéines LEA de la base de données LEAdb, un premier calcul aveugle aboutirait à une moyenne un peu surestimée.
# lecture des données
lea <- lit.dar("http://www.info.univ-angers.fr/~gh/Datasets/lea.dar")
lng <- lea$length
# données manquantes ?
cat(" il y a ",sum(is.na(lng))," valeurs manquantes pour la longueur\n")
# pour plus de sureté :
lng <- na.omit(lng)
# calculs ET graphiques
gr("leadblng1.png")
decritQT("longueur en aa dans LEAdb",lng,"aa",TRUE)
dev.off()
il y a 0 valeurs manquantes pour la longueur
DESCRIPTION STATISTIQUE DE LA VARIABLE longueur en aa dans LEAdb
Taille 773 individus
Moyenne 205.6882 aa
Ecart-type 148.5962 aa
Coef. de variation 72 %
1er Quartile 130.0000 aa
Mediane 168.0000 aa
3eme Quartile 236.0000 aa
iqr absolu 106.0000 aa
iqr relatif 63.0000 %
Minimum 68 aa
Maximum 1864 aa
Tracé tige et feuilles
The decimal point is 2 digit(s) to the right of the |
0 | 777778888888999999999999999999999999999999999999999999999999999999999999999999
1 | 0000000000000000000000000000000000000000000000011111111111111111111111111111111111111111111122222222222223333333333333+273
2 | 0000000000000000000000000000111111111111111122222222222222333333333333333333333333333333333333333444444444444444444444+57
3 | 000000011111222223333344444445556666788889999
4 | 0011111112223444556666777778889
5 | 0122455667888
6 | 22344588
7 | 234
8 | 5
9 |
10 |
11 |
12 | 4
13 |
14 | 3
15 | 1
16 |
17 |
18 | 6
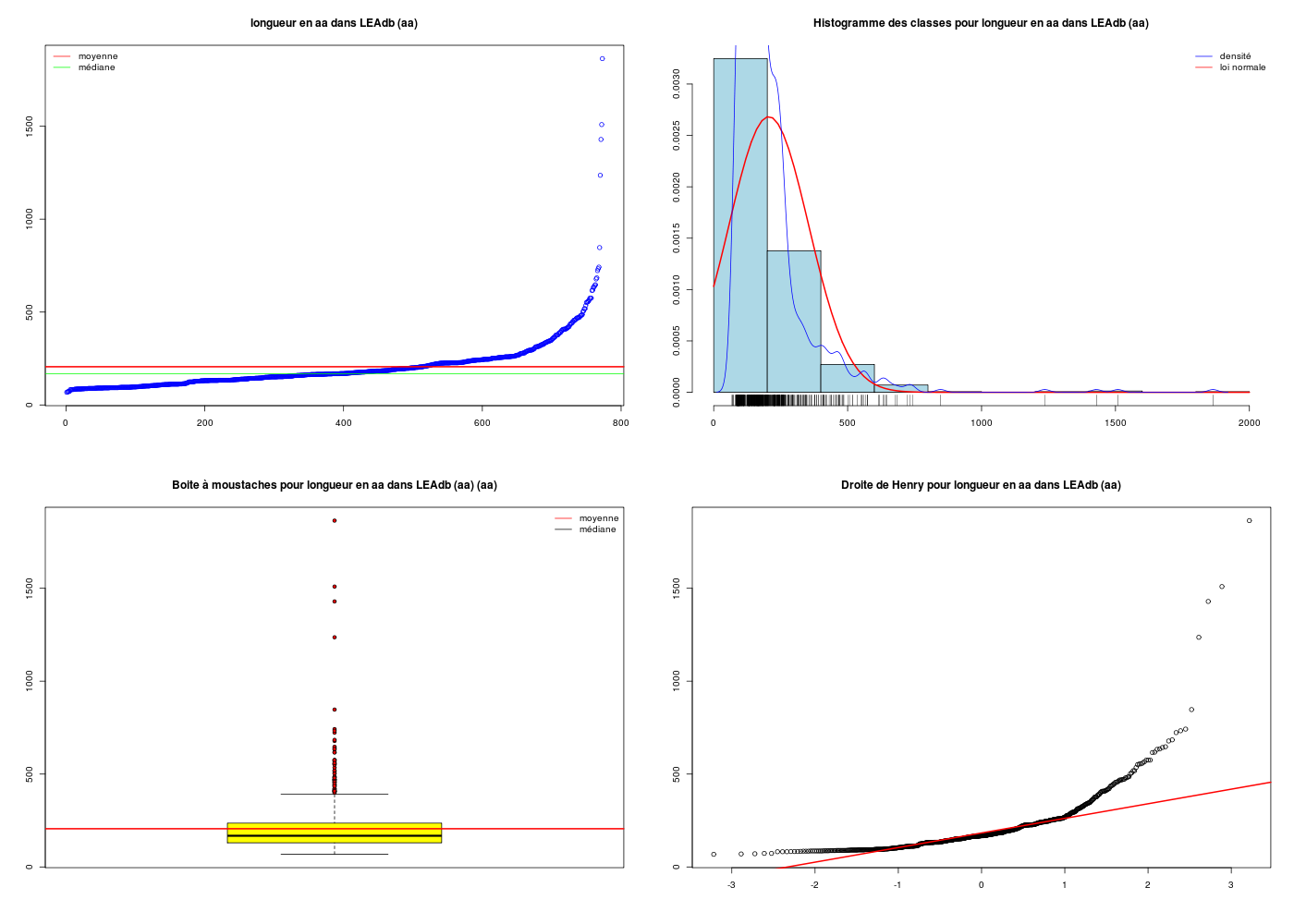
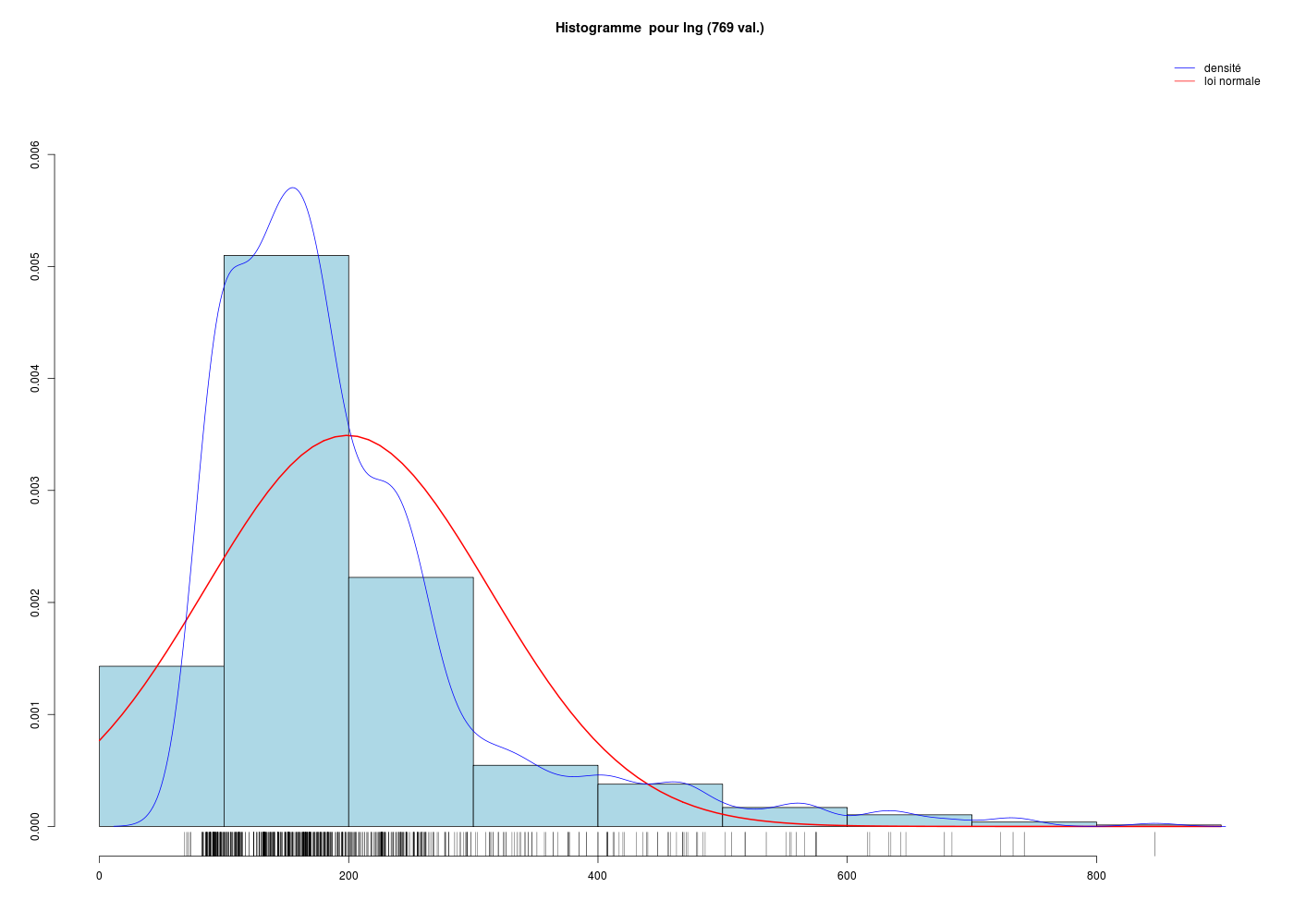
Au vu de la distribution et surtout des grandes valeurs extrêmes, nous avons décidé de filtrer les longueurs :
# après réflexion, on ne garde que les longueurs < 900 aa
lng2 <- lng[ lng < 900 ]
# à nouveau, calculs ET graphiques
gr("leadblng2.png")
decritQT("longueur filtrée en aa dans LEAdb (avec filtre)",lng2,"aa",TRUE)
dev.off()
# sans doute le seul graphique à retenir
scr(1)
gr("leadblng3.png")
histoQT("lng",lng2)
dev.off()
DESCRIPTION STATISTIQUE DE LA VARIABLE longueur filtrée en aa dans LEAdb (avec filtre)
Taille 769 individus
Moyenne 198.9064 aa
Ecart-type 114.1854 aa
Coef. de variation 57 %
1er Quartile 128.0000 aa
Mediane 168.0000 aa
3eme Quartile 234.0000 aa
iqr absolu 106.0000 aa
iqr relatif 63.0000 %
Minimum 68 aa
Maximum 847 aa
Tracé tige et feuilles
The decimal point is 2 digit(s) to the right of the |
0 | 777778888888999999999999999999999999999999999999999999999999999999999999999999
1 | 0000000000000000000000000000000000000000000000011111111111111111111111111111111111111111111122222222222223333333333333+69
1 | 5555555555555555555555555555555555555555555666666666666666666666666666666666666666677777777777777777777777777777777777+74
2 | 0000000000000000000000000000111111111111111122222222222222333333333333333333333333333333333333333444444444444444444444
2 | 5555555555555555555556666666666666666666666666777777788888889999999
3 | 00000001111122222333334444444
3 | 5556666788889999
4 | 0011111112223444
4 | 556666777778889
5 | 01224
5 | 55667888
6 | 22344
6 | 588
7 | 234
7 |
8 |
8 | 5
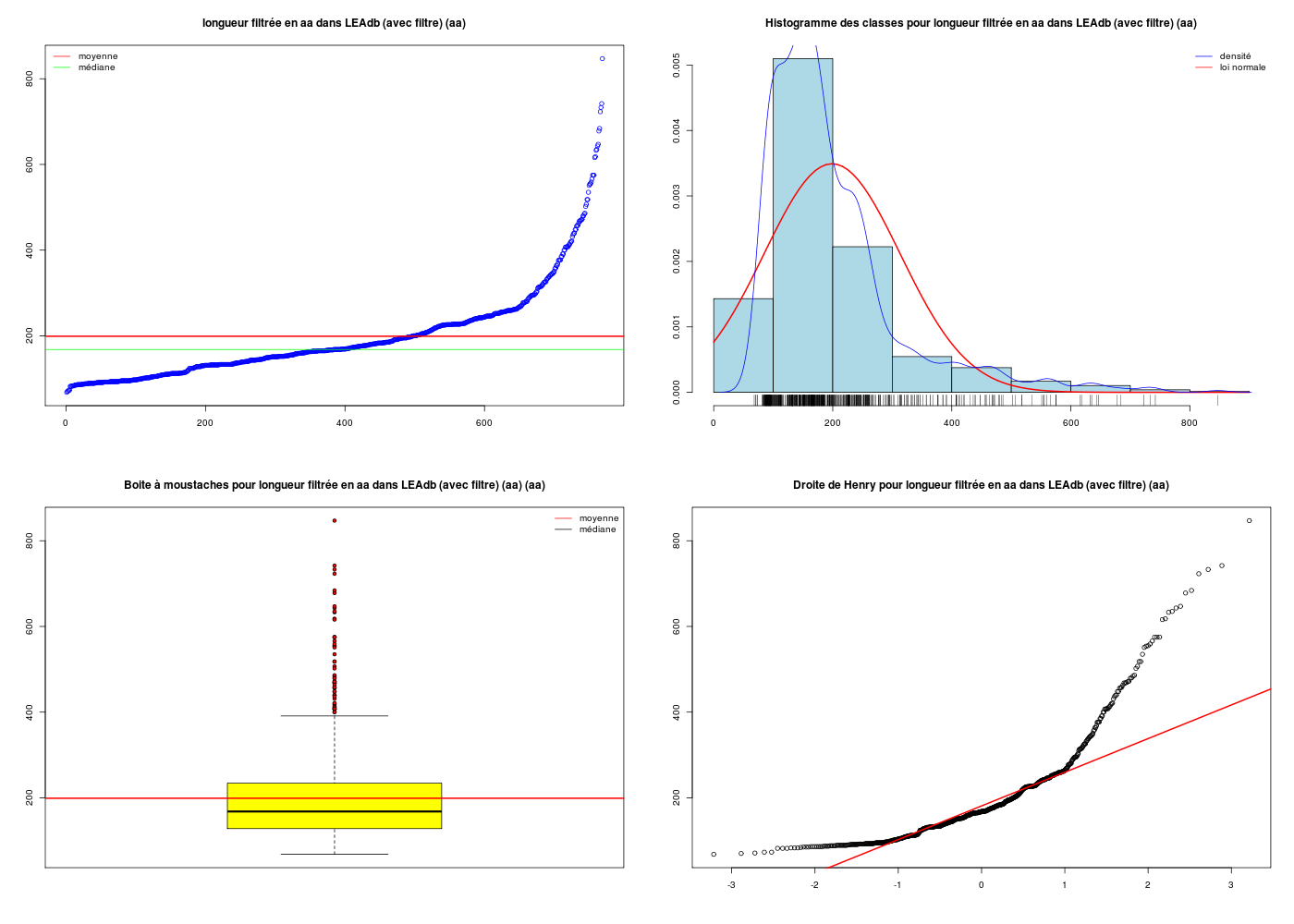
Au final, il y a de nombreuses protéines dont la longueur est inférieure à 234 (valeur de q3), mais pour savoir si des longueurs pareilles sont vraiment courantes, c'est une autre histoire ! Le lecteur ou la lectrice intéréssé(e) par la rédaction associée à ces valeurs pourra consulter la page bism[...]redaction.
Les représentations associées aux variables quantitatives en général sont le tracé direct des valeurs quand elles ne sont pas trop nombreuses, le boxplot et l'histogramme des classes. Pour la distribution des données, on utilise aussi la droite de Henry ou qqplot qui fournit un test visuel de normalité.
2. Utilisation de R, Rstudio, Rcmdr et rkward
Réaliser les calculs et tracer les graphiques de l'exercice précédent avec les 4 interfaces R, Rstudio, Rcmdr et rkward pour les données longueur des protéines dans la LEAdb. Pour la lecture des données, on pourra charger lea.Rdata.
Qu'en déduisez-vous sur ces interfaces ?
2.1 avec R "nu"
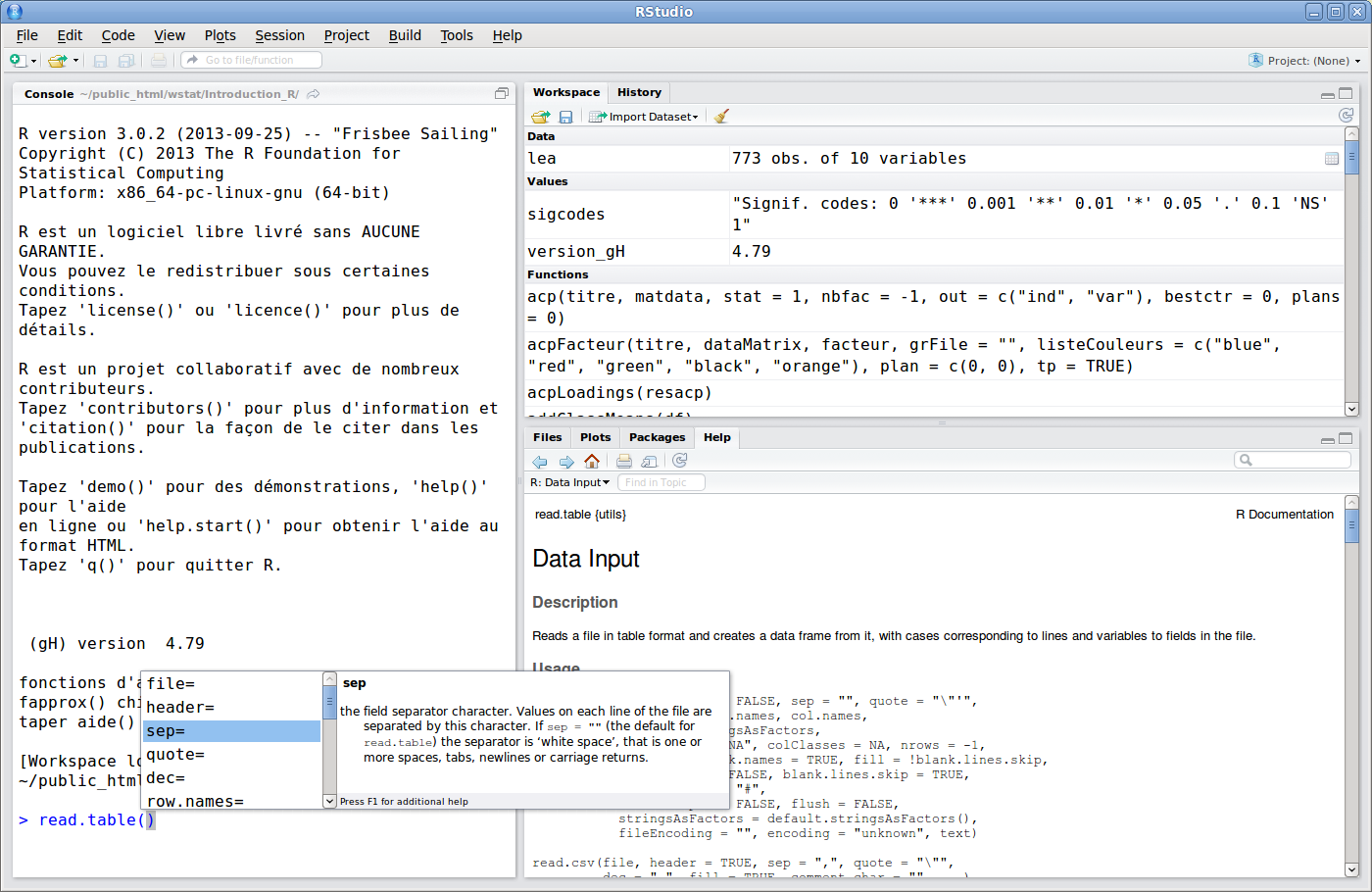
L'interface de base R est en général assez frustre, que ce soit avec rterm.exe ou rgui.exe sous Windows, R ou R -g Tk & sous Linux. Sous windows, il y a bien des menus, mais aucun ne permet de lire des données autrement qu'en chargeant tout un environnement de travail. Dans tous les cas, le plus simple est de taper la commande de chargement des données, à savoir load("lea.Rdata") à moins de préferer la lecture des données sous Internet, avec la fonction classique de R nommée read.table() ou notre fonction dédiée lit.dar.
> leav1 <- read.table("http://www.info.univ-angers.fr/~gh/Datasets/lea.dar",header=TRUE,row.names=1)
> leav2 <- lit.dar("http://www.info.univ-angers.fr/~gh/Datasets/lea.dar")
> identical( leav1, leav2)
TRUE
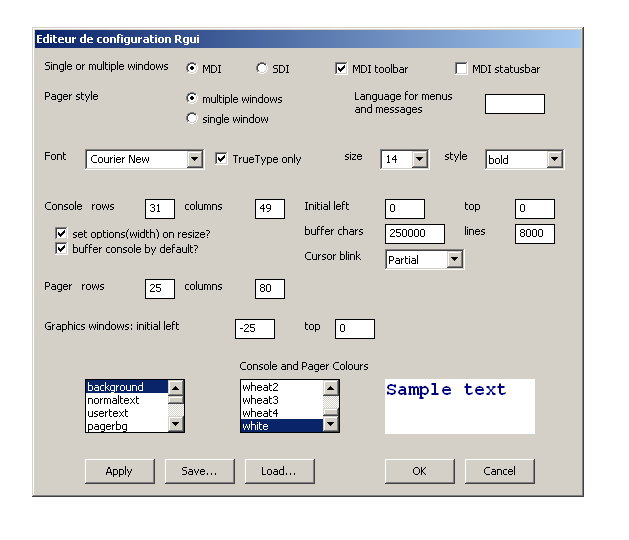
Avec Rgui, il est toutefois possible de gérer l'apparence de la fenêtre et des menus, des sorties via le menu Edition, sous-menu Préférences :
Ensuite, il faut taper toutes les commandes. Heureusement, la touche Tabulation fait des merveilles. Ainsi appuyer sur cette touche juste après le point de read. affiche toutes les commandes possibles en fonction des packages chargés, appuyer sur cette touche juste après la parenthèse dans read.table( affiche tous les paramètres possibles. Merci R !
> read. # ici on a appuyé sur la touche Tabulation
read.csv read.csv2 read.dcf read.delim read.delim2 read.DIF read.fortran read.ftable read.fwf read.socket read.table
> read.table( # ici on a appuyé sur la touche Tabulation
file= quote= col.names= colClasses= check.names= blank.lines.skip= flush= encoding=
header= dec= as.is= nrows= fill= comment.char= stringsAsFactors= text=
sep= row.names= na.strings= skip= strip.white= allowEscapes= fileEncoding=
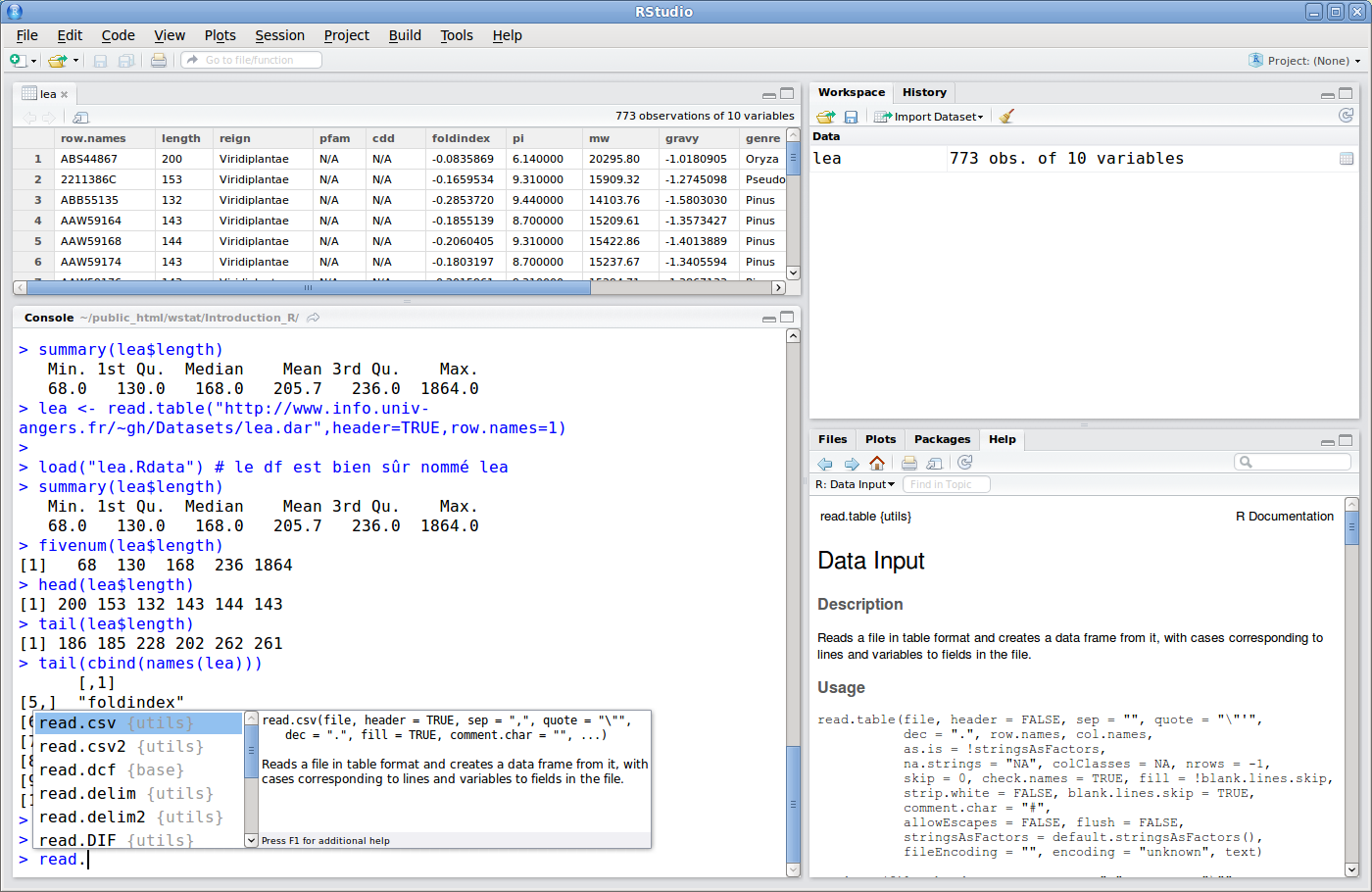
2.2 avec Rstudio
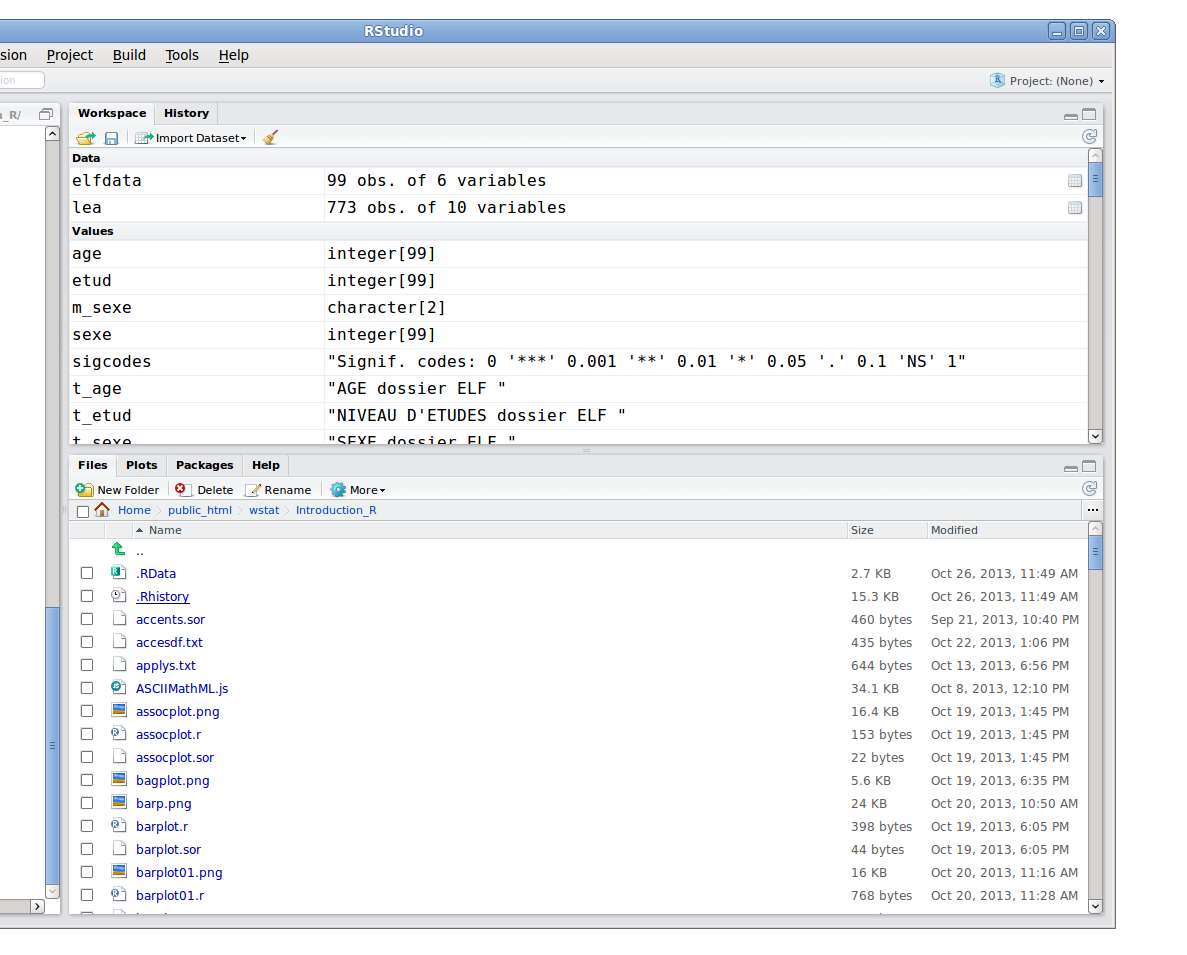
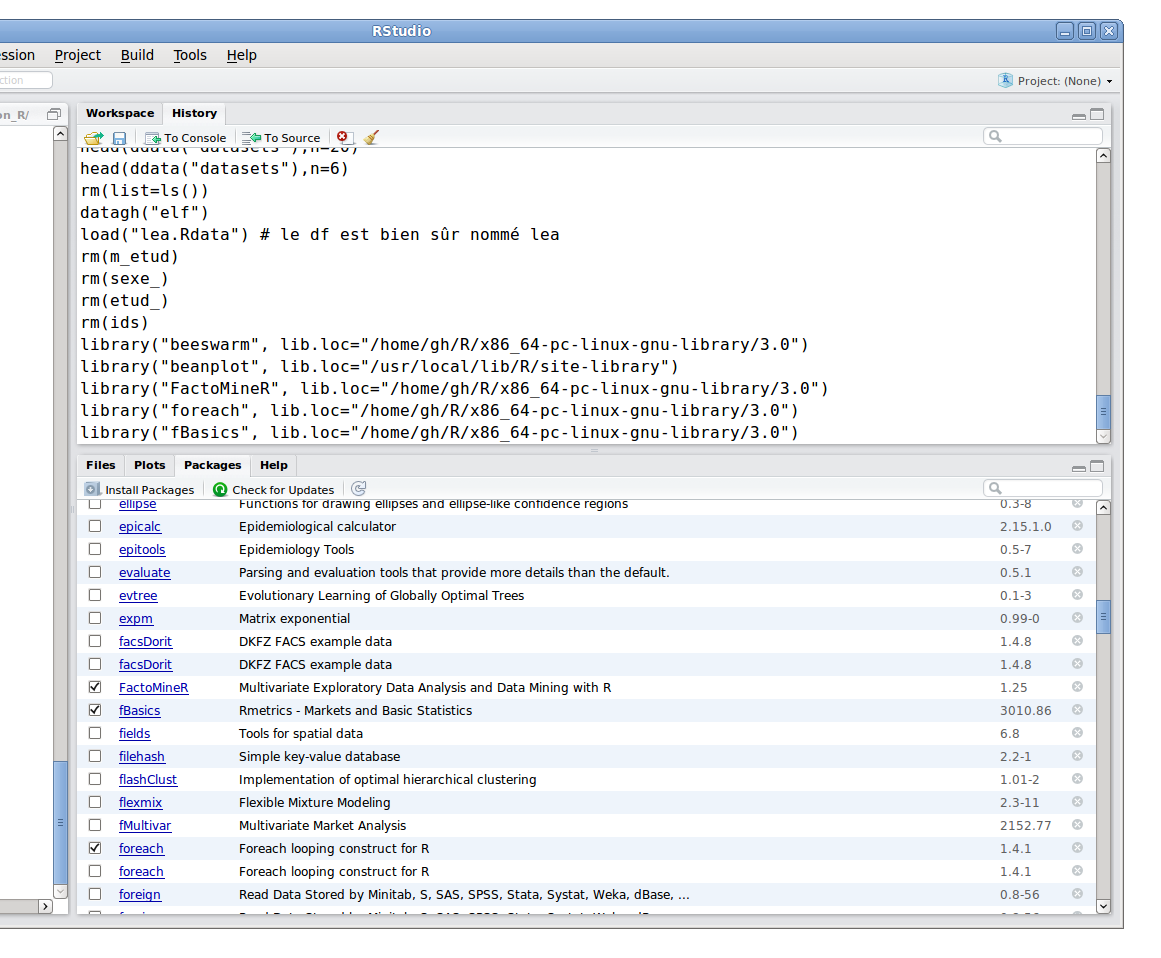
Avant la version 0.95, Rstudio ne fournissait aucune commande pour lire des données, là encore, autrement qu'en chargement un espace de travail. Les versions récentes ont un menu Import Dataset dans le panneau Environment qui gère quelques options... Rstudio fournit un environnement très complet pour taper des commandes et exécuter des programmes. Ainsi, la touche tabulation affiche non seulement les commandes mais aussi les paramètres, Rstudio sait fournir le nom des variables pour les listes et dataframes en notation $.
Rstudio dispose aussi de nombreuses fenêtres qui sont retaillables, il y a un panneau pour les packages, un explorateur de fichier simplifié, une liste des variables et des fonctions, un panneau pour l'historique des commandes, on peut naviguer dans les pages d'aides consultées etc., bref il s'agit d'un environnement très complet qui peut même exécuter Rcmdr.
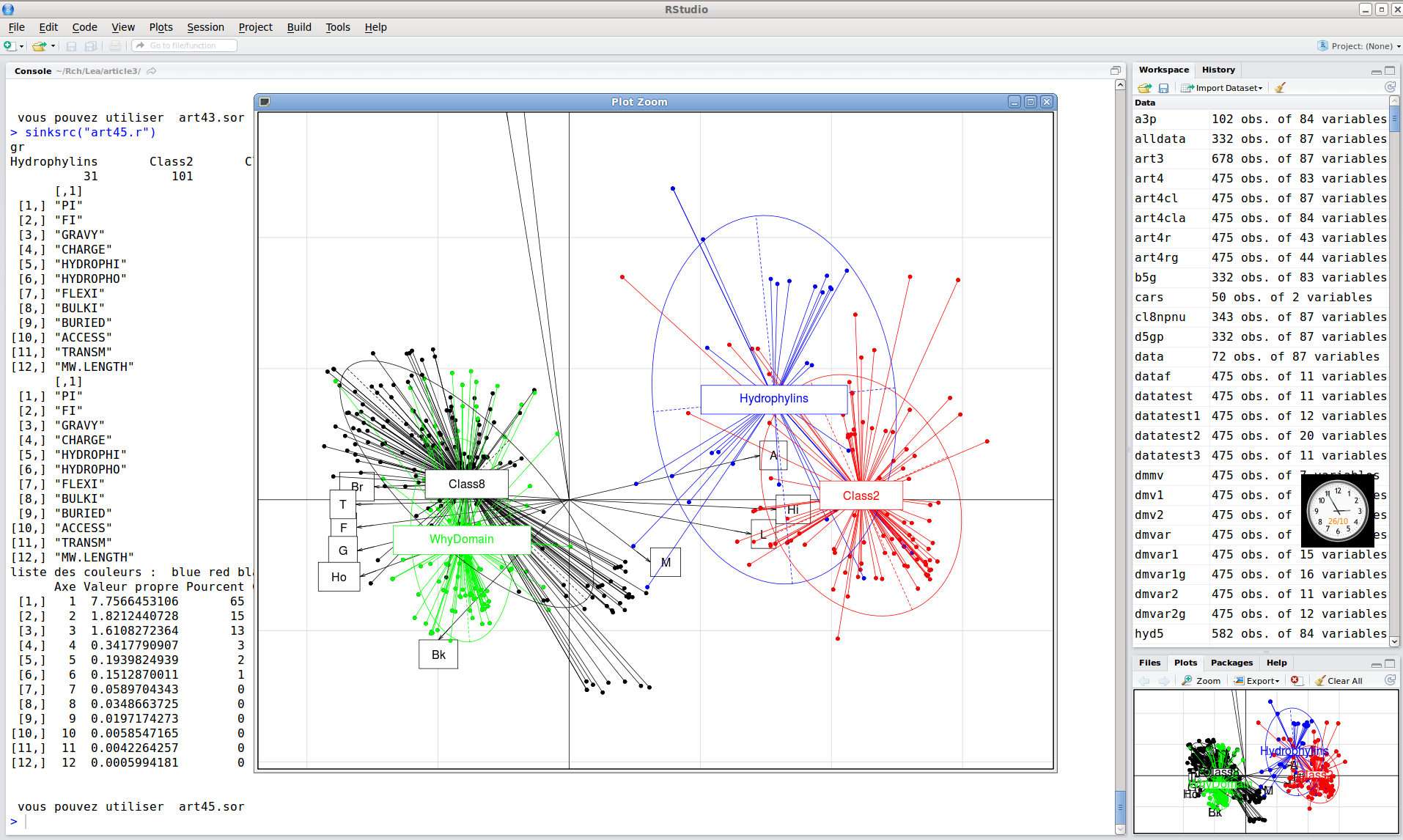
Enfin, Rstudio permet de naviguer d'un graphique à l'autre, fournir un zoom, des exports...
2.3 avec Rcmdr
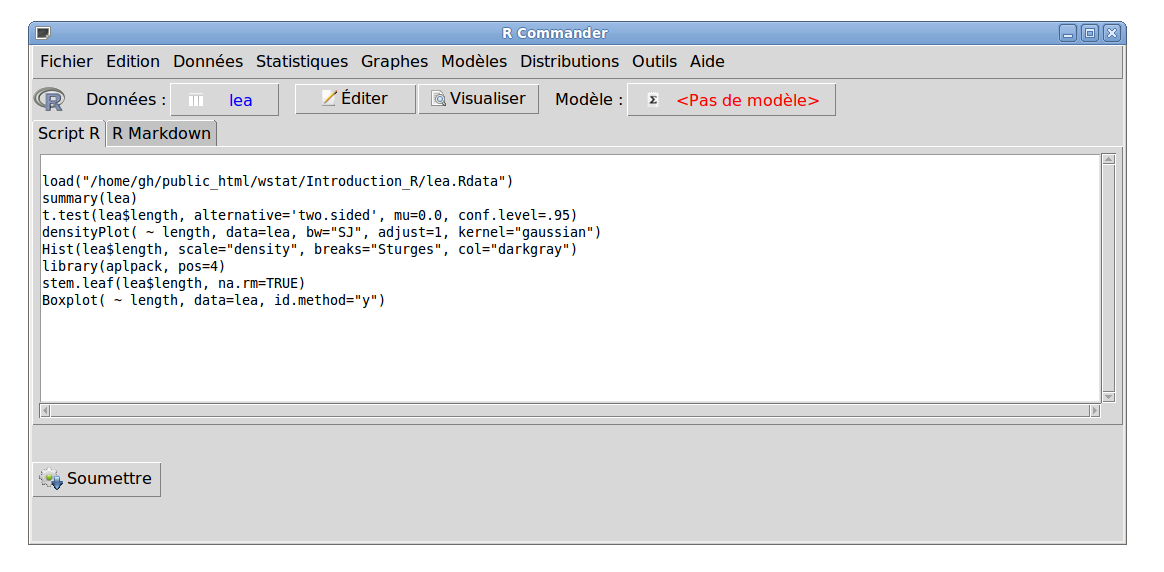
Avant de pouvoir utiliser Rcmdr, il faut l'installer via install.packages("Rcmdr"). Pour utiliser Rcmdr, il faut passer par R "nu" ou Rstudio et là, taper library(Rcmdr). Dans l'interface qui apparait, on clique sur le menu Données puis sur Charger un jeu de données. Après avoir sélectionné ou saisi lea.Rdata cliquer sur ouvrir active le jeu de données chargé.
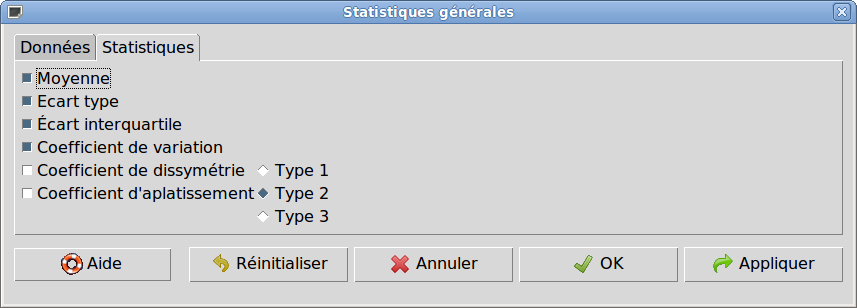
L'analyse statistique se fait via le menu Statistiques, sous-menu Résumés, sous-sous-menu Statistiques descriptives. Après avoir sélectionné length dans la liste des variables (onglet Données) et rajouté le coefficient de variation (onglet Statistiques), il suffit de cliquer sur Ok pour voir les indicateurs statistiques demandés dans la sortie courante de R.
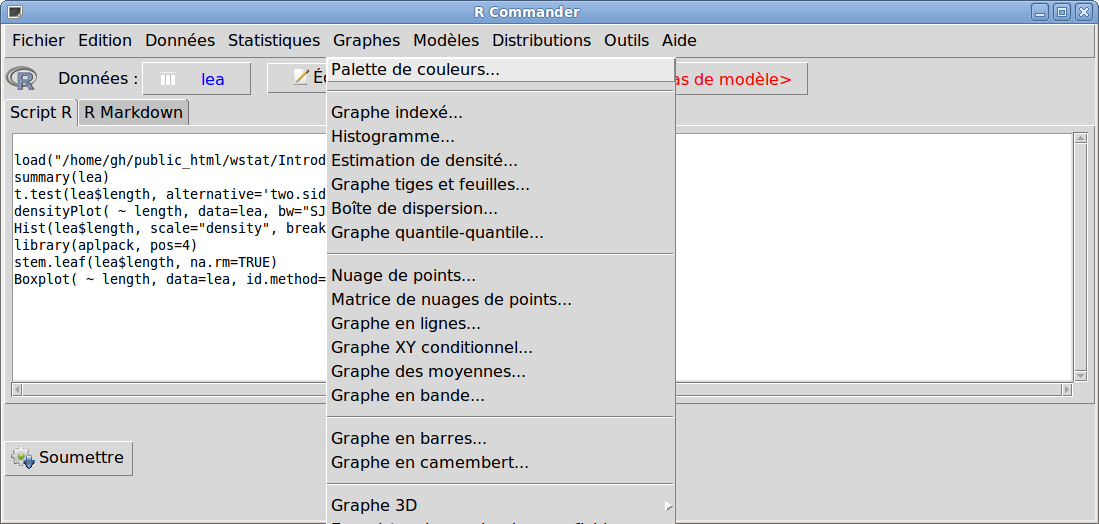
Pour tracer l'histogramme, le box plot (nommé ici Boite de dispersion), il suffit de passer par le le menu Graphes. On en profitera pour regarder à chaque fois les options proposées.
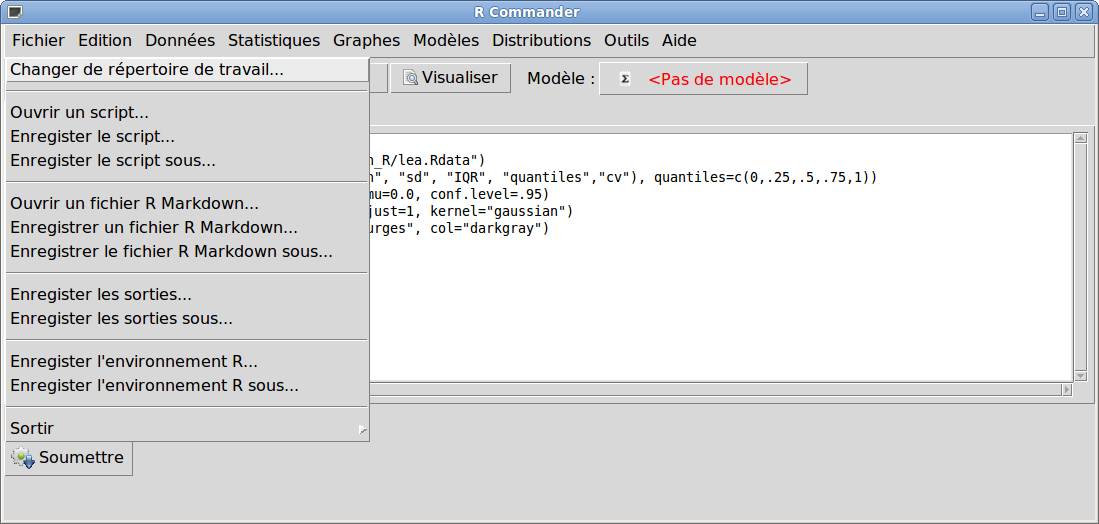
Une fois les calculs et graphiques effectués, on quitte Rcmdr via le menu Fichier sous-menu Sortir ; il est alors possible de sauvegarder les commandes, les résultats...
2.4 avec rkward
Si rkward est un exécutable qui s'exécute hors de R ou de Rstudio, son fonctionnement est assez similaire dans le principe à Rcmdr. Pour charger le fichier lea.Rdata, il faut passer par le menu Fichier, sous-menu Importer, sous-sous-menu Load R datafile (tiens, un partie de menu non traduite !), pour réaliser l'analyse statistique, il faut utiliser le menu Analysis, sous-menu Descriptive Statistics, on s'en serait douté...
2.5 discussion des interfaces
L'interface de R est sans doute trop minimaliste pour convenir à une utilisation courante, sauf si on possède de grands écrans et si maitrise bien les commandes et fonctions de R. Rstudio parait, à l'usage, sans doute le meilleur compromis entre le choix des commandes et l'aide aux tâches usuelles de visualisation, sauvegarde, mise en forme.
Rcmdr est très intéressant en initiation et pour découvrir des options, des commandes, une certaine façon de faire, notamment pour la modélisation. Rcmdr dispose de nombreux plugins, mais rkward est sans doute plus complet au niveau des menus et des possibilités. Malheureusement pour de nombreux utilisateurs français tout n'est pas traduit pour rkward et, de plus, ce qui est source de difficulté, rkward requiert une installation à part de R.
Rcmdr est suffisamment connu et utilisé pour qu'on trouve de nombreuses aides sur le Web y compris en français, et il y a même des vidéos pour apprendre à s'en servir.
Par contre, en 2013, le wiki associé est presque vide. C'est aussi le cas pour le cas du wiki de rkward. A propos, que pensez-vous du wiki français pour R par rapport au wiki anglais ?
3. Calculs statistiques par série
Comment calculer les moyennes des colonnes d'un data frame ? Et leurs médianes ?
Comment rajouter ces informations en bas du data frame ?
Comme données d'essai, on pourra utiliser les variables de prix par année dans le dossier LOGEMENT.
Comment calculer des moyennes par classe, par exemple des moyennes d'ages par sexe dans le dossier HER ?
Y a-t-il des représentations graphiques associées ?
Il est très facile de calculer les moyennes par colonne puisqu'il existe en R une fonction colMeans(). Par contre, et c'est à peine plus difficile, il faut passer par apply() pour calculer les médianes par colonne. Ensuite, on utilise rbind() pour ajouter ces informations comme lignes supplémentaires des données.
# lecture des données
logement <- lit.dar("http://www.info.univ-angers.fr/~gh/Datasets/logement.dar")
# calcul des moyennes en colonnes à l'aide de colMeans
moys <- colMeans( logement)
# calcul des médianes en colonnes à l'aide de apply
meds <- apply(X=logement,FUN=median,MARGIN=2)
# avant :
print(tail(logement))
onames <- row.names(logement)
# ajout des moyennes et médianes
logement <- rbind( logement, moys, meds )
row.names(logement) <- c(onames,"Moyennes","Médianes")
# après :
print(tail(round(logement,1)))
> # lecture des données
>
> logement <- lit.dar("http://www.info.univ-angers.fr/~gh/Datasets/logement.dar")
> # calcul des moyennes en colonnes à l'aide de colMeans
>
> moys <- colMeans( logement)
> # calcul des médianes en colonnes à l'aide de apply
>
> meds <- apply(X=logement,FUN=median,MARGIN=2)
> # avant :
>
> print(tail(logement))
MI70 MX70 MI80 MX80 MI82 MX82 MI86 MX86 MI88 MX88
AR/M 12 18 48 60 60 100 70 120 70 140
LGrM 12 25 35 90 56 122 75 130 80 140
Arca 18 22 57 107 65 156 90 165 95 165
Roya 15 20 50 90 62 138 90 160 100 150
BAUL 14 28 70 120 70 160 100 250 120 270
DEAU 14 20 55 100 71 120 65 160 70 160
> onames <- row.names(logement)
> # ajout des moyennes et médianes
>
> logement <- rbind( logement, moys, meds )
> row.names(logement) <- c(onames,"Moyennes","Médianes")
> # après :
>
> print(tail(round(logement,1)))
MI70 MX70 MI80 MX80 MI82 MX82 MI86 MX86 MI88 MX88
Arca 18.0 22.0 57.0 107.0 65.0 156 90.0 165.0 95.0 165.0
Roya 15.0 20.0 50.0 90.0 62.0 138 90.0 160.0 100.0 150.0
BAUL 14.0 28.0 70.0 120.0 70.0 160 100.0 250.0 120.0 270.0
DEAU 14.0 20.0 55.0 100.0 71.0 120 65.0 160.0 70.0 160.0
Moyennes 17.4 28.2 64.3 108.3 83.2 152 103.3 188.1 117.0 216.9
Médianes 15.0 25.0 58.0 100.0 73.0 139 82.5 155.0 87.5 162.5
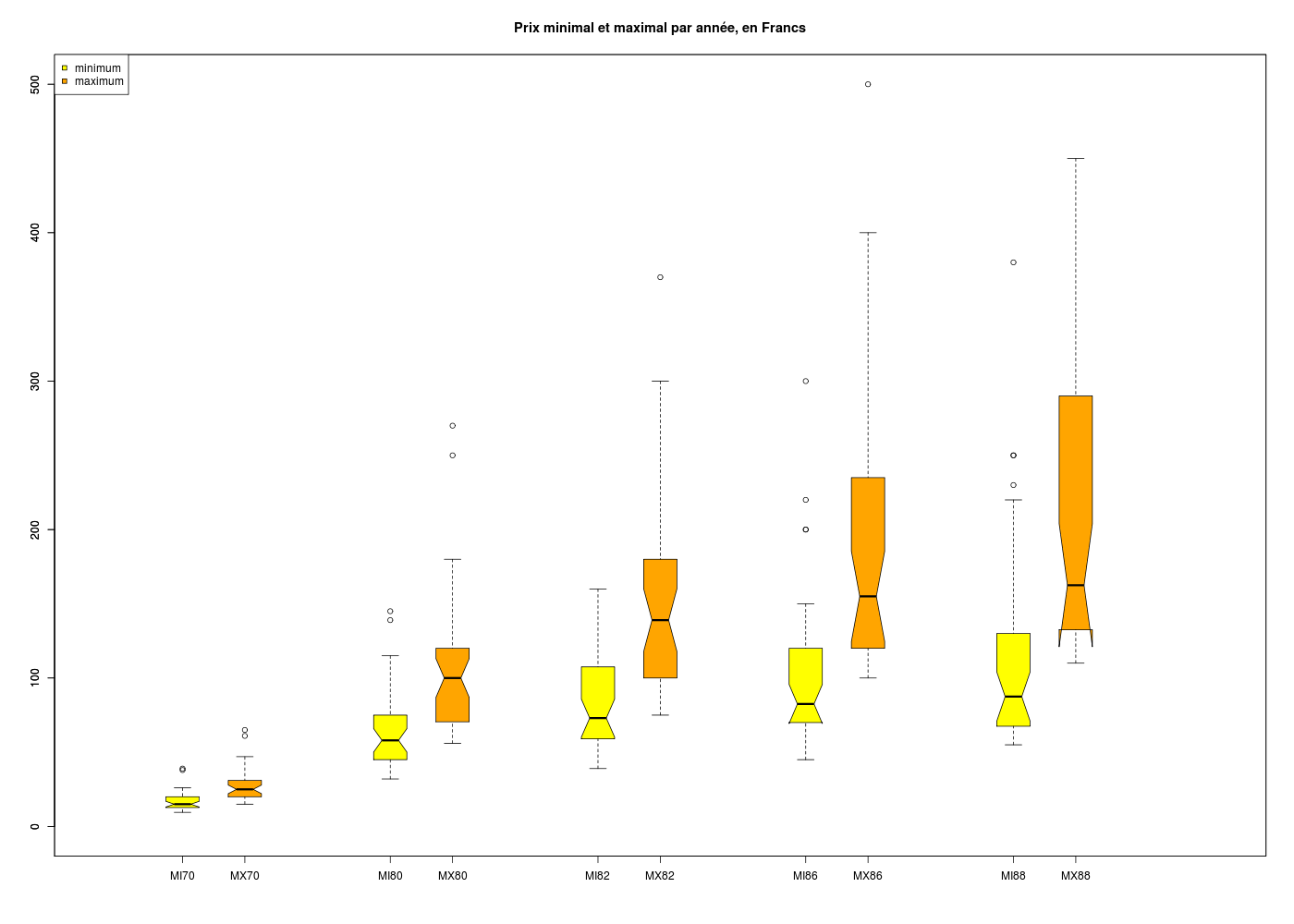
On associe classiquement les boxplots aux calculs pour des variables quantitatives.
# lecture des données
logement <- lit.dar("http://www.info.univ-angers.fr/~gh/Datasets/logement.dar")
# tracé des minima
pdv <- 1:5
limx <- c(0,27)
limy <- c(0,max(logement))
boxplot(logement[,2*pdv-1],at=5*pdv-3,col="yellow",notch=TRUE,xlim=limx,ylim=limy)
# tracé des maxima
boxplot(logement[,2*pdv],at=5*pdv-1.5,col="orange",notch=TRUE,add=TRUE,xlim=limx,ylim=limy)
# titre et légende
title(main="Prix minimal et maximal par année, en Francs")
legend(x="topleft",legend=c("minimum","maximum"),pt.bg=c("yellow","orange"),pch=22,col="black")
Il est beaucoup moins fréquent (et non prévu par R) d'afficher les moyennes et leurs intervalles de confiance, mais avec quelques connaissances en R, il est possible de les afficher à coté des boxplots :
# lecture des fonctions (gH)
source("http://www.info.univ-angers.fr/~gh/statgh.r",encoding="latin1")
# lecture des données avec une fonction (gH)
logement <- lit.dar("http://www.info.univ-angers.fr/~gh/Datasets/logement.dar")
# tracé des minima
pdv <- 1:5
limx <- c(1,25)
limy <- c(0,max(logement))
mins <- 2*pdv-1
maxs <- mins + 1
boxplot(logement[,mins],at=5*pdv-3,col="yellow",notch=TRUE,xlim=limx,ylim=limy)
# tracé des maxima
boxplot(logement[,maxs],at=5*pdv-1.5,col="orange",notch=TRUE,add=TRUE,xlim=limx,ylim=limy)
# ajout des moyennes
moys <- colMeans(logement)
points(5*pdv-4,moys[mins],pch=18,col="blue")
points(5*pdv-0.5,moys[maxs],pch=18,col="darkgreen")
# deux fonctions bien pratiques
minic <- function(x) { return( t.test(x)$conf.int[1] ) }
maxic <- function(x) { return( t.test(x)$conf.int[2] ) }
# on représente les intervalles de confiance avec des flèches
mic <- apply(X=logement,FUN=minic,MARGIN=2)
mac <- apply(X=logement,FUN=maxic,MARGIN=2)
arrows(5*pdv-4,mic[mins],5*pdv-4,mac[mins],col="black",angle=75,code=3)
arrows(5*pdv-0.5,mic[maxs],5*pdv-0.5,mac[maxs],col="black",angle=75,code=3)
# titre et légende
title(main="Prix minimal et maximal par année, en Francs")
legend(x="topleft",legend=c("minimum","maximum","moyenne"),pt.bg=c("yellow","orange","blue"),pch=c(22,22,18),col="blue")
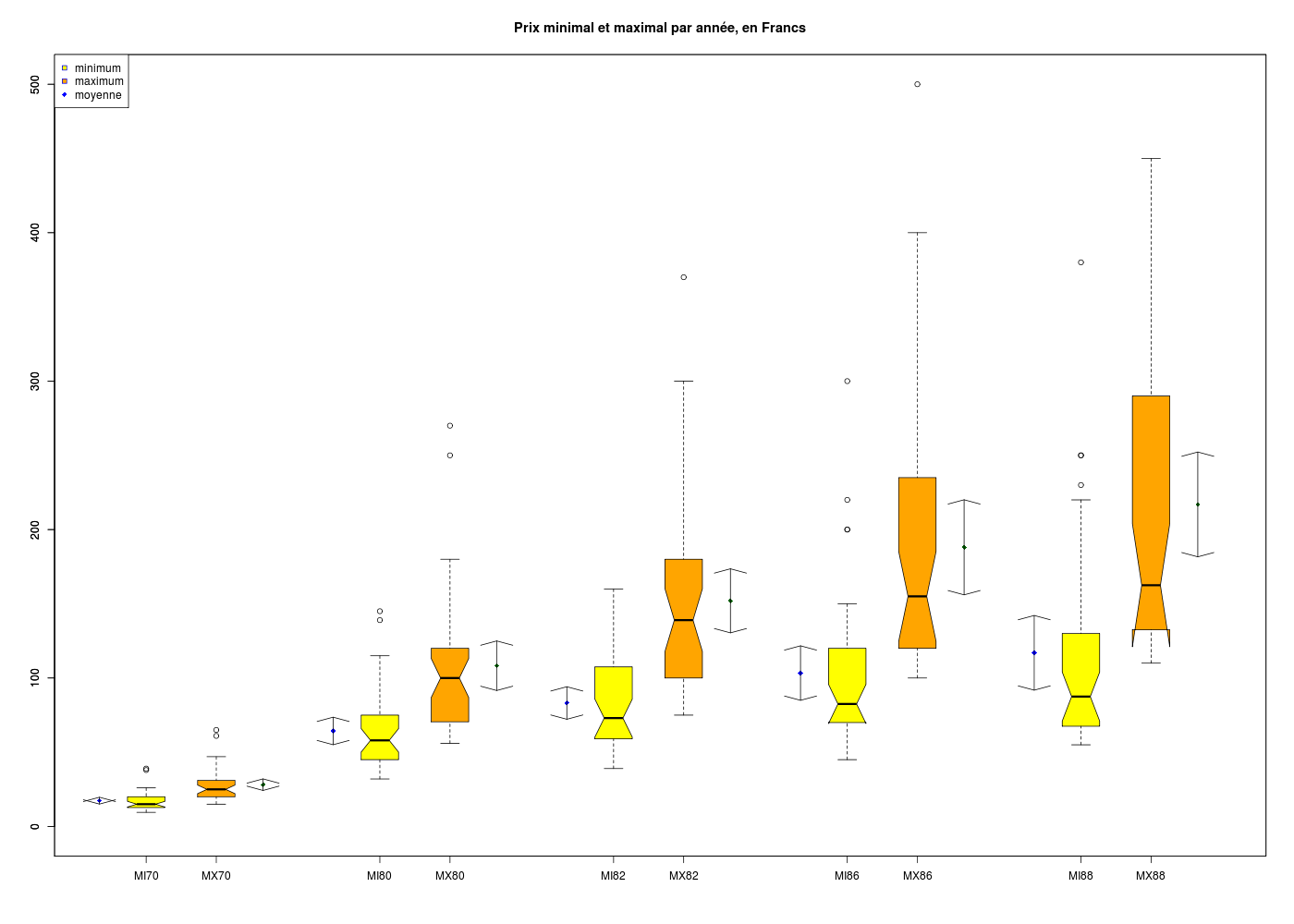
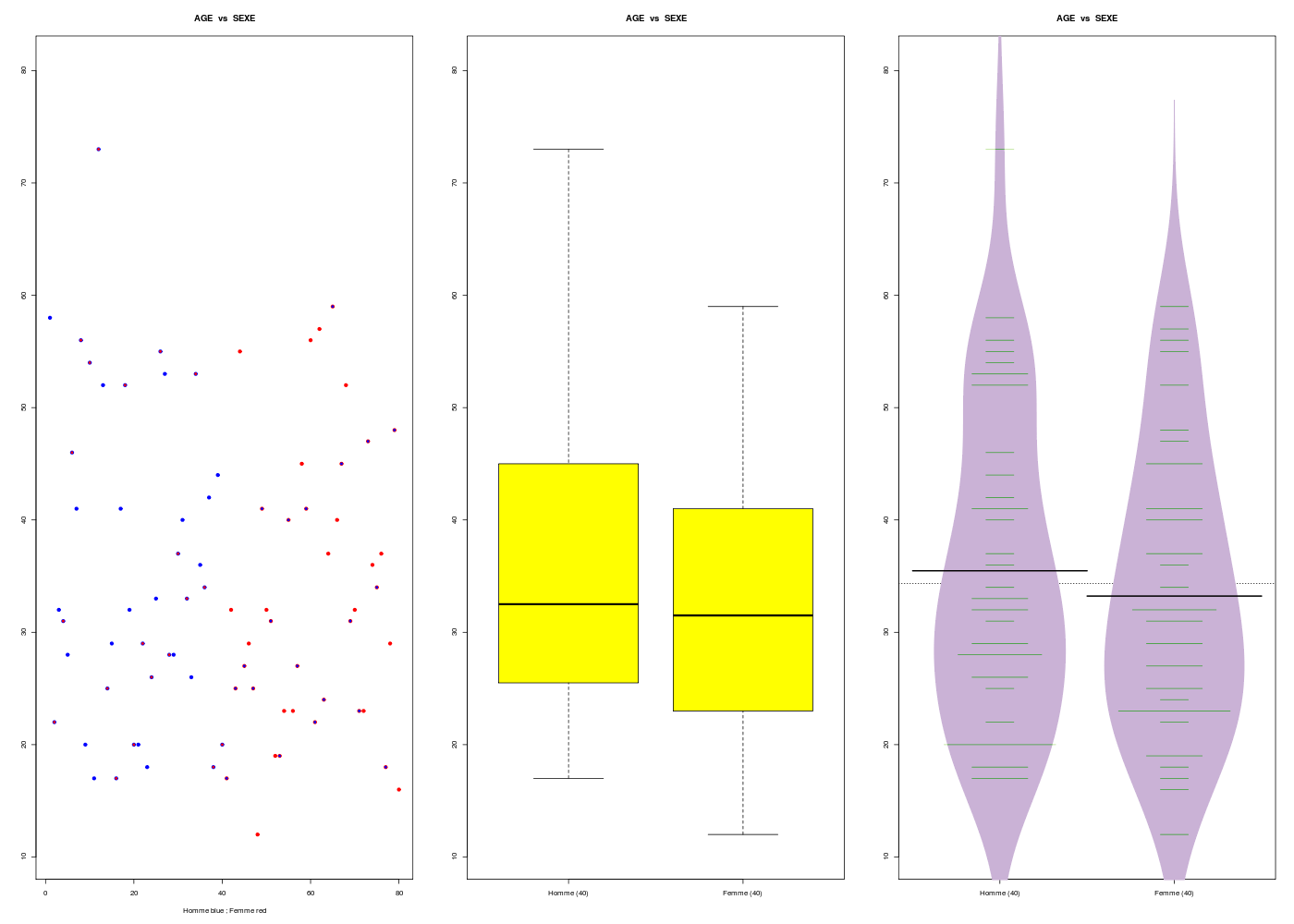
Pour tracer des boxplots sur des sous-groupes, on utilise la notation ~ (tilde), qui se lit en fonction de. Nous montrons aussi comment calculer par sous-groupe :
# lecture des données et définition des modalités
her <- lit.dar("http://www.info.univ-angers.fr/~gh/Datasets/her.dar")
attach(her)
sexeql <- factor(sexe,levels=0:1,labels=c("Homme","Femme"))
# calculs sur l'age par sexe (1)
cats("Avec deux vecteurs séparés")
ageshom <- age[ sexeql=="Homme" ]
agesfam <- age[ sexeql=="Femme" ]
print( summary(ageshom) )
print( summary(agesfam) )
# calculs sur l'age par sexe (2)
cats("Via une liste grace à split")
decoupe <- split(x=age,f=sexeql)
print( lapply(X=decoupe,FUN=summary) )
# calculs sur l'age par sexe (3)
cats("Si on utilise tapply")
print( tapply(X=age,INDEX=sexeql,FUN=summary) )
## tracés associés
gr("herage.png")
par(mfrow=c(1,2))
# version courte
boxplot(age~sexeql)
# version longue
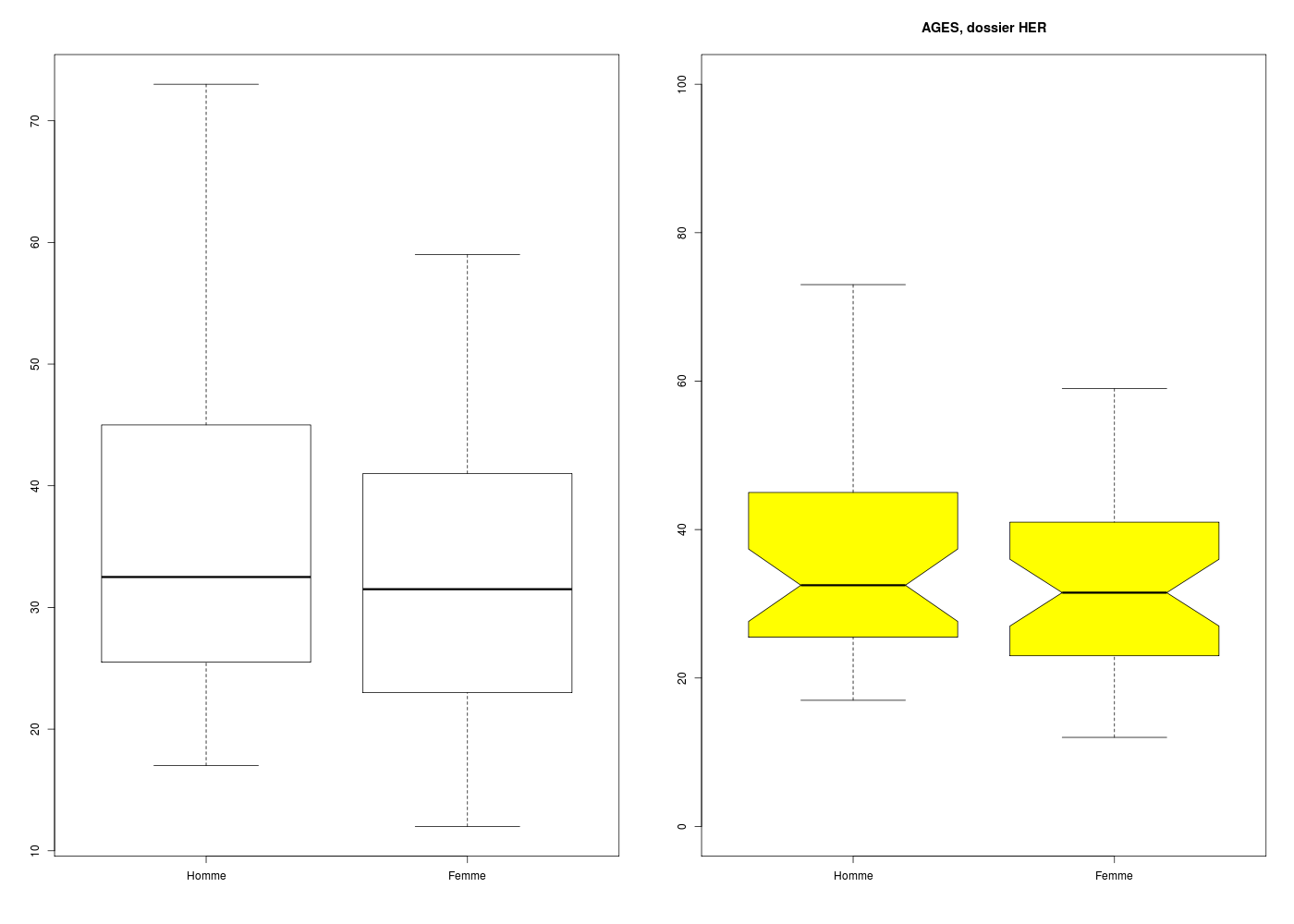
boxplot(age~sexeql,col="yellow",main="AGES, dossier HER",ylim=c(0,100),notch=TRUE)
# fermeture du fichier graphique
dev.off()
# retour à un graphique
par(mfrow=c(1,1))
# à ne pas oublier :
detach(her)
# avec la fonction (gH) nommée decritQTparFacteur
gr("herage2.png")
decritQTparFacteur(titreQT="AGE",nomVarQT=her$age,unite="ans",titreQL="SEXE",nomVarQL=her$sexe,labels=c("Homme","Femme"),graphique=TRUE)
dev.off()
Avec deux vecteurs séparés
==========================
Min. 1st Qu. Median Mean 3rd Qu. Max.
17.00 25.75 32.50 35.48 44.50 73.00
Min. 1st Qu. Median Mean 3rd Qu. Max.
12.00 23.00 31.50 33.22 41.00 59.00
Via une liste grace à split
===========================
$Homme
Min. 1st Qu. Median Mean 3rd Qu. Max.
17.00 25.75 32.50 35.48 44.50 73.00
$Femme
Min. 1st Qu. Median Mean 3rd Qu. Max.
12.00 23.00 31.50 33.22 41.00 59.00
Si on utilise tapply
====================
$Homme
Min. 1st Qu. Median Mean 3rd Qu. Max.
17.00 25.75 32.50 35.48 44.50 73.00
$Femme
Min. 1st Qu. Median Mean 3rd Qu. Max.
12.00 23.00 31.50 33.22 41.00 59.00
RStudioGD
2
VARIABLE QT AGE ,unit=ans
VARIABLE QL SEXE labels : Homme Femme
N Moy Unite Ect Cdv Q1 Med Q3 EIQ Min Max
Global 80 34.350 ans 13.093 38 23.750 32.000 42.500 18.750 12.000 73.000
Homme 40 35.475 ans 13.751 39 25.750 32.500 44.500 18.750 17.000 73.000
Femme 40 33.225 ans 12.297 37 23.000 31.500 41.000 18.000 12.000 59.000
Analysis of Variance Table
Response: nomVarQT
Df Sum Sq Mean Sq F value Pr(>F)
ql 1 101.2 101.25 0.5801 0.4486
Residuals 78 13613.0 174.53
Kruskal-Wallis rank sum test
data: nomVarQT by ql
Kruskal-Wallis chi-squared = 0.3621, df = 1, p-value = 0.5473
4. Tris à plat et tris croisés
Qu'est-ce qu'un tri à plat ? Et un tri croisé ? Comment les calculer en R ?
Y a-t-il des représentations graphiques associées ?
Comment ajouter des marges à un tableau de comptages, à un tableau de fréquences ?
Comme données d'essai, on pourra utiliser les variables survie et classe du dossier TITANIC.
Un tri à plat est l'analyse classique d'une variable qualitative. Il est d'usage d'afficher les pourcentages plutôt que les comptages pour faciliter la comparaison des variables qualitatives et d'ordonner les résultats par fréquence décroissante pour faire ressortir les modalités les plus importantes. Un tri croisé est l'analyse des croisements des modalités de deux variables qualitatives. Plusieurs tableaux relatifs sont possibles (pourcentages par rapport à la ligne, la colonne, le total général).
# lecture des données et définition des modalités
titanic <- lit.dar("http://www.info.univ-angers.fr/~gh/Datasets/titanic.dar")
cablab <- c("équipage","première classe","seconde classe","troisième classe")
survie <- factor(titanic$SURV,levels=0:1,labels=c("décédé","survivant"))
cabine <- factor(titanic$CLASS,levels=0:3,labels=cablab)
# comptages (fréquences absolues)
cats("Effectifs")
print( table(survie) )
# fréquences relatives
cats("Effectifs relatifs")
print( table(survie)/length(survie) )
# pourcentages
cats("un tap (tri à plat)")
frq <- table(survie)/length(survie)
print( round(100*frq,0) )
# pour les cabines, ce n'est pas trié
cats("presque un tap (tri à plat)")
frq <- table(cabine)/length(cabine)
print( round(100*frq,0) )
# avec le tri décroissant
cats("un tap (tri à plat) pour cabine")
frq <- table(cabine)/length(cabine)
idx <- order(frq,decreasing=TRUE)
print( round(100*frq[idx],0) )
# graphiques associés
gr("titanic1.png")
par(mfrow=c(2,2))
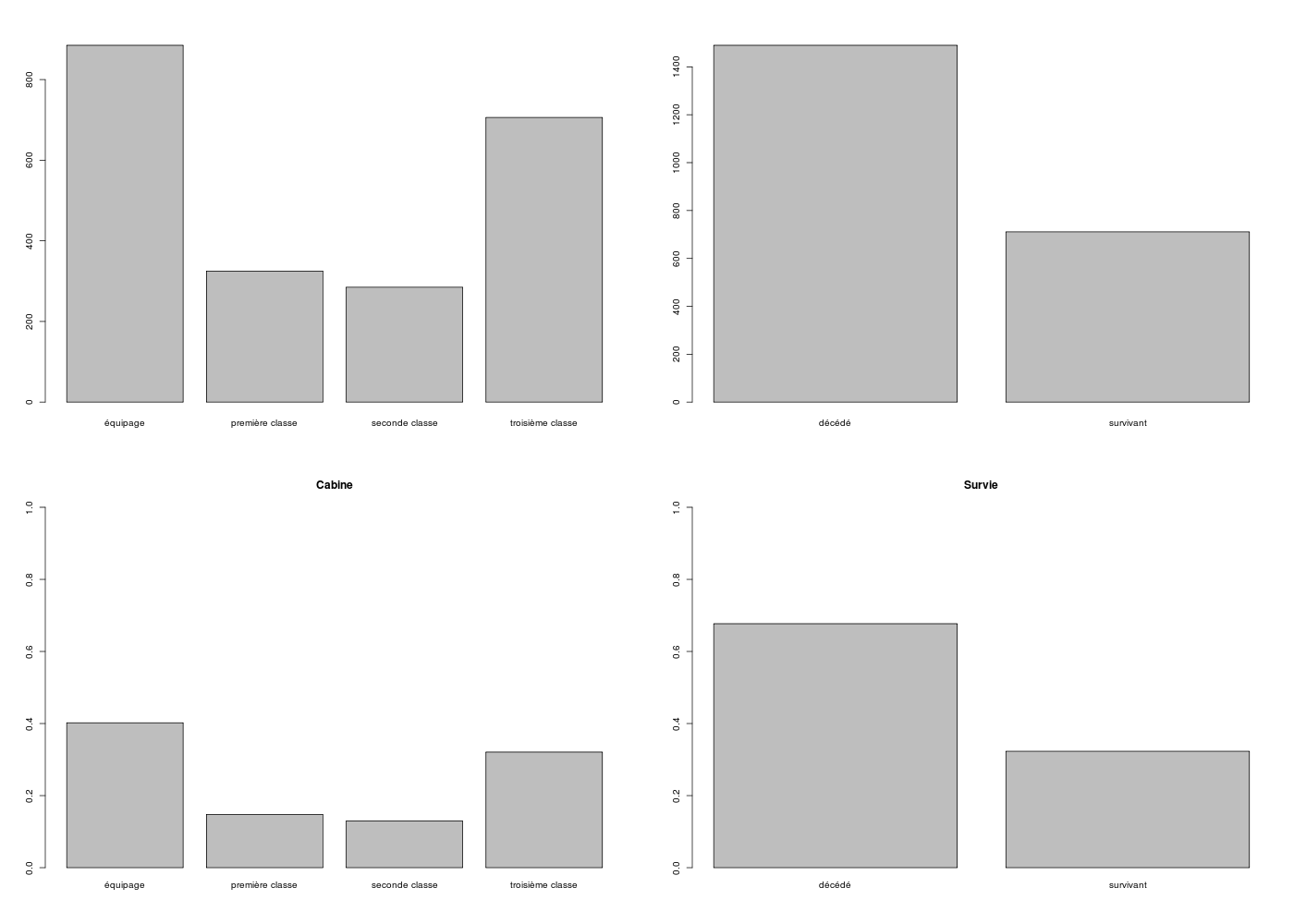
barplot( table(cabine) )
barplot( table(survie) )
barplot( table(cabine)/length(cabine),ylim=c(0,1),main="Cabine")
barplot( table(survie)/length(survie),ylim=c(0,1),main="Survie")
dev.off()
par(mfrow=c(1,1))
# un tri croisé
table(survie, cabine)
# et son transposé
table(cabine,survie)
# ajoutons les marges
t1 <- table(cabine,survie)
t2 <- addmargins(A=t1,margin=1,FUN=sum)
t3 <- addmargins(A=t2,margin=2,FUN=sum)
cats("avec marges")
print(t3)
# graphiques associés, que choisir ?
gr("titanic2.png")
par(mfrow=c(2,2))
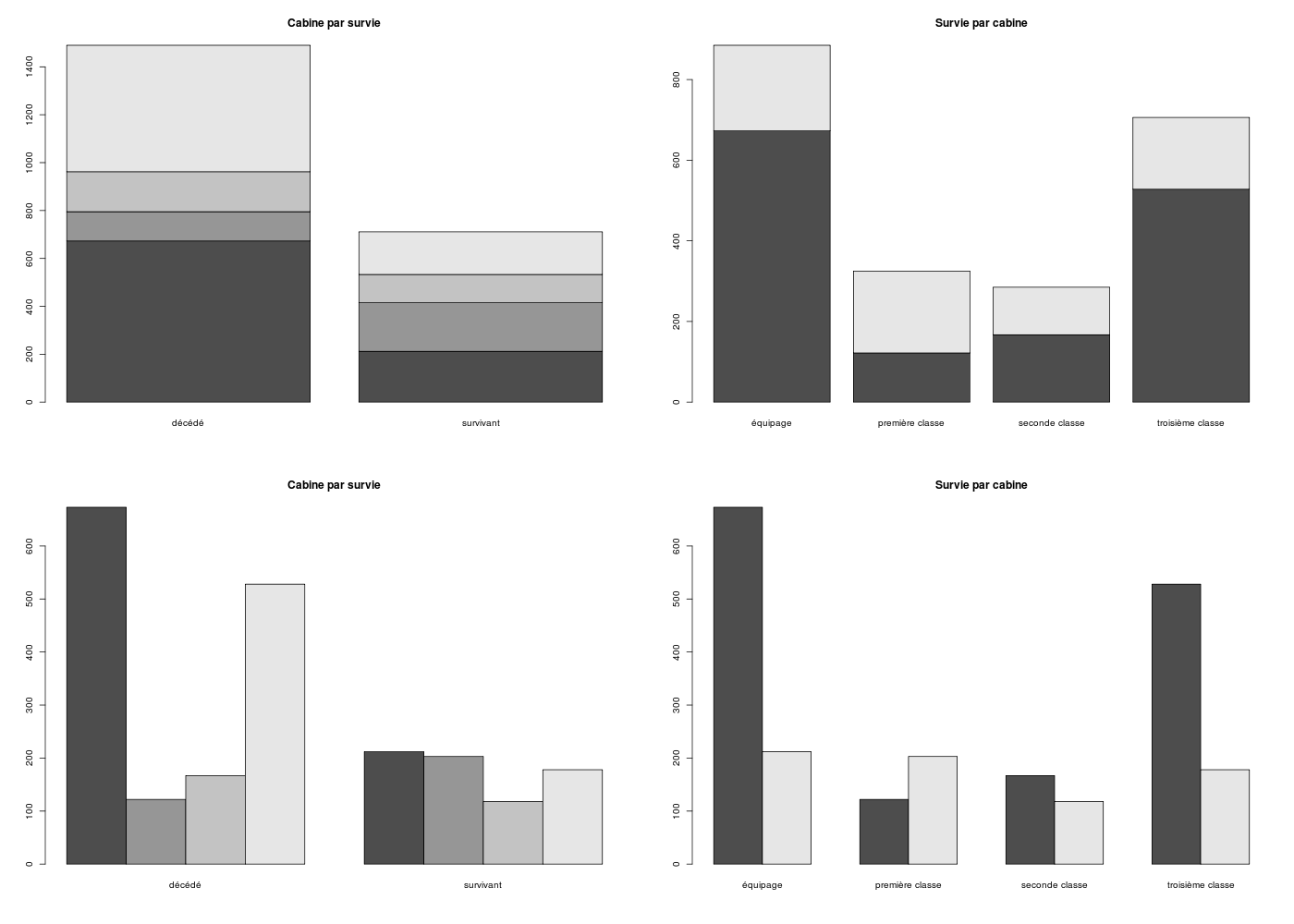
barplot( table(cabine,survie),main="Cabine par survie" )
barplot( table(survie,cabine),main="Survie par cabine" )
barplot( table(cabine,survie),beside=TRUE,main="Cabine par survie")
barplot( table(survie,cabine),beside=TRUE,main="Survie par cabine")
dev.off()
par(mfrow=c(1,1))
Effectifs
=========
survie
décédé survivant
1490 711
Effectifs relatifs
==================
survie
décédé survivant
0.676965 0.323035
un tap (tri à plat)
===================
survie
décédé survivant
68 32
presque un tap (tri à plat)
===========================
cabine
équipage première classe seconde classe troisième classe
40 15 13 32
un tap (tri à plat) pour cabine
===============================
cabine
équipage troisième classe première classe seconde classe
40 32 15 13
cabine
survie équipage première classe seconde classe troisième classe
décédé 673 122 167 528
survivant 212 203 118 178
survie
cabine décédé survivant
équipage 673 212
première classe 122 203
seconde classe 167 118
troisième classe 528 178
avec marges
===========
survie
cabine décédé survivant sum
équipage 673 212 885
première classe 122 203 325
seconde classe 167 118 285
troisième classe 528 178 706
sum 1490 711 2201
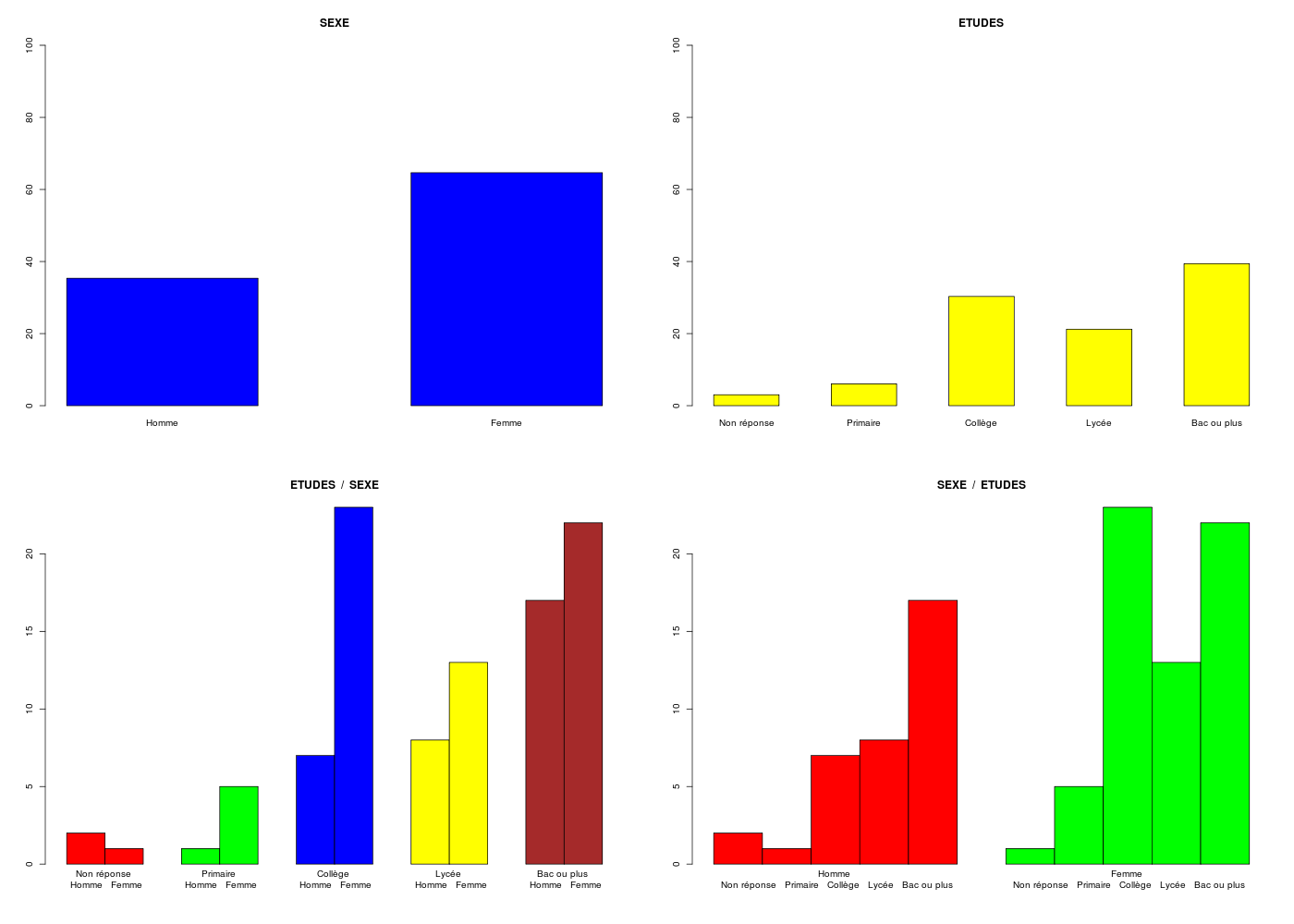
Comme nous l'avions dit dans la séance précédente, les graphiques associés aux tris à plat sont les histogrammes de fréquences que l'on trace en R via barplot() pour les pourcentages, car sinon on risque d'induire en erreur toute personne qui ne fait pas attention aux axes. Pour les tris croisés, il est conseillé de tracer un "barplot" non empilé à l'aide du paramètre beside et de ne retenir éventuellement, parmi les deux barplots possibles, que celui qui montre des informations différentes des tris à plat.
Nos fonctions triAplat() et triCroise() automatisent bien sûr ces calculs et tracés.
# lecture des données et définition des modalités
elf <- lit.dar("http://www.info.univ-angers.fr/~gh/Datasets/elf.dar")
labsexe <- c("Homme","Femme")
labetud <- c("Non réponse","Primaire","Collège","Lycée","Bac ou plus")
triAplat("SEXE (dossier ELF)",elf$SEXE,"Homme Femme")
decritQL(titreQL="SEXE (dossier ELF)",nomVar=elf$SEXE,labelMod="Homme Femme",ordreModalites=TRUE)
gr("elfql.png")
triCroise("SEXE",elf$SEXE,labsexe,"ETUDES",elf$ETUD,labetud,TRUE)
dev.off()
> # lecture des données et définition des modalités
> elf <- lit.dar("http://www.info.univ-angers.fr/~gh/Datasets/elf.dar")
> labsexe <- c("Homme","Femme")
> labetud <- c("Non réponse","Primaire","Collège","Lycée","Bac ou plus")
> triAplat("SEXE (dossier ELF)",elf$SEXE,"Homme Femme")
TRI A PLAT DE : SEXE (dossier ELF)
Homme Femme Total
Effectif 35 64 99
Cumul Effectif 35 99 99
Frequence (en %) 35 65 100
Cumul fréquences 35 100 100
> decritQL(titreQL="SEXE (dossier ELF)",nomVar=elf$SEXE,labelMod="Homme Femme",ordreModalites=TRUE)
TRI A PLAT DE : SEXE (dossier ELF) (ordre des modalités)
Homme Femme Total
Effectif 35 64 99
Cumul Effectif 35 99 99
Frequence (en %) 35 65 100
Cumul fréquences 35 100 100
VARIABLE : SEXE (dossier ELF) (par fréquence décroissante)
Femme Homme Total
Effectif 64 35 99
Cumul Effectif 35 99 99
Frequence (en %) 65 35 100
Cumul fréquences 65 100 100
> gr("elfql.png")
> triCroise("SEXE",elf$SEXE,labsexe,"ETUDES",elf$ETUD,labetud,TRUE)
TRI CROISE DES QUESTIONS :
SEXE (en ligne)
ETUDES (en colonne)
Effectifs
Non réponse Primaire Collège Lycée Bac ou plus
Homme 2 1 7 8 17
Femme 1 5 23 13 22
Effectifs avec totaux
Non réponse Primaire Collège Lycée Bac ou plus Total
Homme 2 1 7 8 17 35
Femme 1 5 23 13 22 64
Total 3 6 30 21 39 99
Valeurs en % du total
Non réponse Primaire Collège Lycée Bac ou plus TOTAL
Homme 2 1 7 8 17 35
Femme 1 5 23 13 22 65
TOTAL 3 6 30 21 39 100
CALCUL DU CHI-DEUX D'INDEPENDANCE
Tableau des données
Homme Femme Total
Non réponse 2 1 3
Primaire 1 5 6
Collège 7 23 30
Lycée 8 13 21
Bac ou plus 17 22 39
Total 35 64 99
Valeurs attendues et marges
Homme Femme Total
Non réponse 1.1 1.9 3
Primaire 2.1 3.9 6
Collège 10.6 19.4 30
Lycée 7.4 13.6 21
Bac ou plus 13.8 25.2 39
Total 35.0 64.0 99
Contributions signées
Homme Femme
Non réponse + 0.832 - 0.455
Primaire - 0.593 + 0.324
Collège - 1.226 + 0.671
Lycée + 0.045 - 0.024
Bac ou plus + 0.748 - 0.409
Valeur du chi-deux 5.326981
Le chi-deux max (table) à 5 % est 9.487729 ; p-value 0.2553618 pour 4 degrés de liberté.
décision : au seuil de 5 % on ne peut pas rejeter l'hypothèse
qu'il y a indépendance entre ces deux variables qualitatives.
Plus fortes contributions avec signe de différence
Signe Valeur Pct Mligne Mcolonne Ligne Colonne Obs Th
- 1.226 23.02 % Collège Homme 3 1 7 10.6
+ 0.832 15.62 % Non réponse Homme 1 1 2 1.1
+ 0.748 14.05 % Bac ou plus Homme 5 1 17 13.8
+ 0.671 12.59 % Collège Femme 3 2 23 19.4
- 0.593 11.13 % Primaire Homme 2 1 1 2.1
- 0.455 8.54 % Non réponse Femme 1 2 1 1.9
- 0.409 7.68 % Bac ou plus Femme 5 2 22 25.2
+ 0.324 6.08 % Primaire Femme 2 2 5 3.9
+ 0.045 0.84 % Lycée Homme 4 1 8 7.4
- 0.024 0.46 % Lycée Femme 4 2 13 13.6
Message d'avis :
In chisq.test(tcr, correct = TRUE) : Chi-squared approximation may be incorrect
5. Exemples de régressions (linéaire, logistique...) et d'analyse de variance
Rappeler la différence entre régression linéaire et régression logistique, entre régression simple et régression multiple.
Modéliser par une relation linéaire la dépendance entre la variable consommation d'essence et la variable distance parcourue dans le jeu de données km.dar. Y a-t-il des représentations graphiques associées ? Pourquoi y a-t-il 4 graphiques produits avec plot(lm(modele)) alors qu'on pourrait en avoir 6 ?
Faut-il envisager une relation de causalité ? Quelles sont les valeurs prédites par le modèle pour 100 et 250 km ?
Peut-on prédire l'appartenance d'une personne au groupe à partir de sa taille, par exemple 166 cm, dans les données pg.dar ?
Peut-on prédire le sexe d'une personne à partir de son age, par exemple 50 ans, dans le dossier ELF ?
Comparer les ages entre les hommes et les femmes dans ce même dossier. On utilisera un seuil α de première espèce de 5 %.
Y a-t-il des représentations graphiques associées ?
Y a-t-il des rapports entre régression linéaire et analyse de la variance ?
Quelles sont les différences entre régression et corrélation ?
Sur les notions de régression linéaire et logistique, de régression simple et multiple, voir la solution de l' exercice 1 de mon cours de niveau 2 à l'école doctorale.
5.1 régression linéaire
Pour définir un modèle linéaire avec R, il faut utiliser la fonction lm() et la droite correspondante se trace directement avec abline(). Pour afficher le modèle, on peut utiliser les fonctions génériques summary() et coef().
# lecture des données
km <- lit.dar("km.dar")
idx <- order(km$distance)
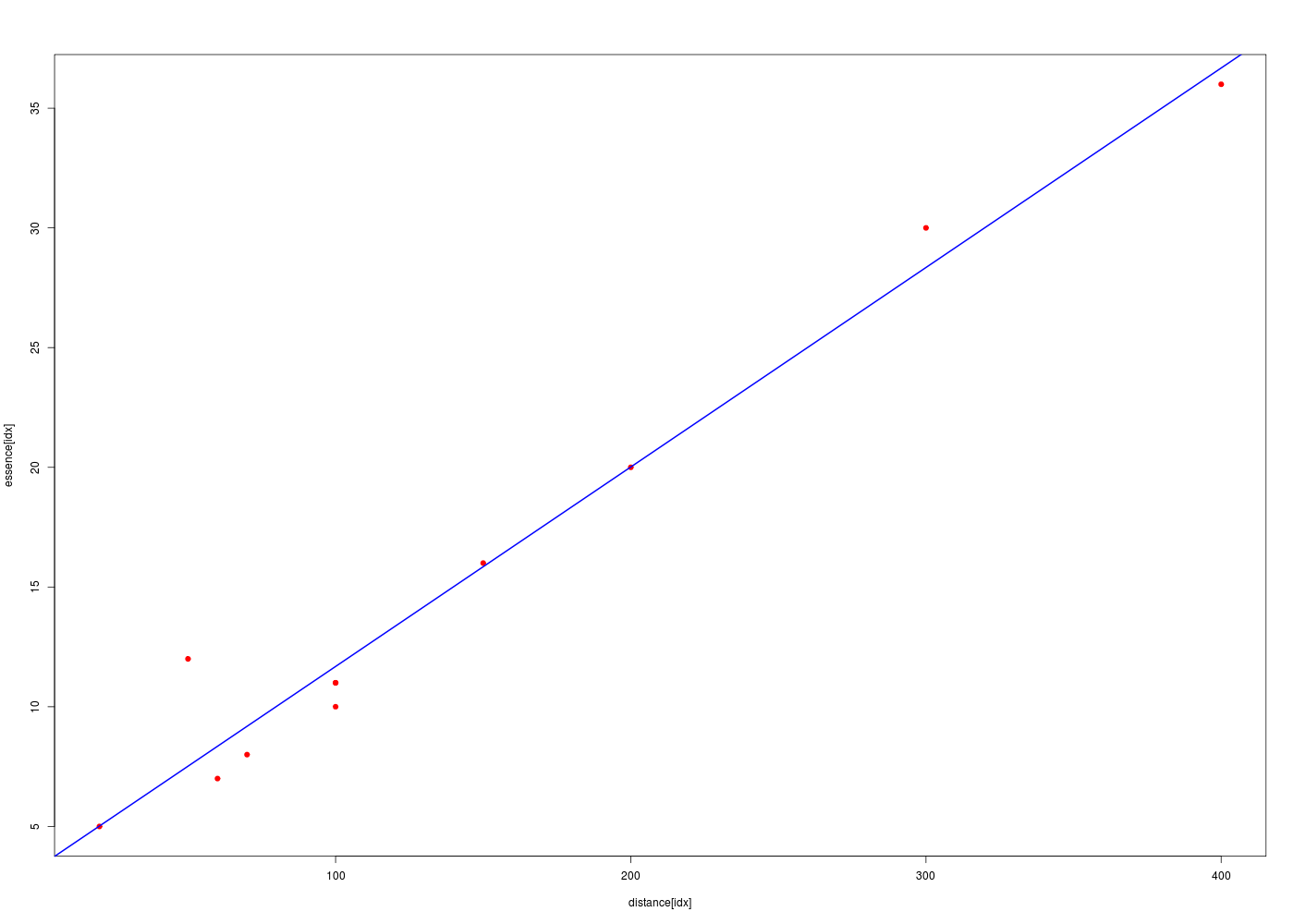
# tracé rapide
# surtout pas
# with( km, plot(essence~distance,type="b") )
with( km, plot(essence[idx]~distance[idx],type="p",pch=19,col="red" ))
# ajout de la droite de régression
ml <- lm(essence ~ distance,data=km) # pas besoin de idx ici
abline(ml, col="blue",lwd=2)
# description du modèle
cats("Modèle linéaire ESSENCE en fonction de DISTANCE")
print( summary(ml) )
# coefficients
cats("coefficients seulement")
print( coef(ml) )
# l'objet issu de lm est complexe
cats("Objet modèle linéaire :")
print( names(ml) )
print( str(ml) )
Modèle linéaire ESSENCE en fonction de DISTANCE
===============================================
Call:
lm(formula = essence ~ distance, data = km)
Residuals:
Min 1Q Median 3Q Max
-1.6824 -0.9326 -0.6783 0.0686 4.4836
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.350376 0.894150 3.747 0.00458 **
distance 0.083320 0.004985 16.714 4.39e-08 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.835 on 9 degrees of freedom
Multiple R-squared: 0.9688, Adjusted R-squared: 0.9653
F-statistic: 279.4 on 1 and 9 DF, p-value: 4.393e-08
coefficients seulement
======================
(Intercept) distance
3.35037574 0.08331991
Objet modèle linéaire :
=======================
[1] "coefficients" "residuals" "effects" "rank" "fitted.values" "assign"
[7] "qr" "df.residual" "xlevels" "call" "terms" "model"
List of 12
$ coefficients : Named num [1:2] 3.3504 0.0833
..- attr(*, "names")= chr [1:2] "(Intercept)" "distance"
$ residuals : Named num [1:11] -0.6824 -0.0144 1.6537 -0.6783 0.1516 ...
..- attr(*, "names")= chr [1:11] "traj0001" "traj0002" "traj0003" "traj0004" ...
$ effects : Named num [1:11] -50.051 -30.669 1.756 -0.609 0.304 ...
..- attr(*, "names")= chr [1:11] "(Intercept)" "distance" "" "" ...
$ rank : int 2
$ fitted.values: Named num [1:11] 11.7 20 28.3 36.7 15.8 ...
..- attr(*, "names")= chr [1:11] "traj0001" "traj0002" "traj0003" "traj0004" ...
$ assign : int [1:2] 0 1
$ qr :List of 5
..$ qr : num [1:11, 1:2] -3.317 0.302 0.302 0.302 0.302 ...
.. ..- attr(*, "dimnames")=List of 2
.. .. ..$ : chr [1:11] "traj0001" "traj0002" "traj0003" "traj0004" ...
.. .. ..$ : chr [1:2] "(Intercept)" "distance"
.. ..- attr(*, "assign")= int [1:2] 0 1
..$ qraux: num [1:2] 1.3 1.19
..$ pivot: int [1:2] 1 2
..$ tol : num 1e-07
..$ rank : int 2
..- attr(*, "class")= chr "qr"
$ df.residual : int 9
$ xlevels : Named list()
$ call : language lm(formula = essence ~ distance, data = km)
$ terms :Classes 'terms', 'formula' length 3 essence ~ distance
.. ..- attr(*, "variables")= language list(essence, distance)
.. ..- attr(*, "factors")= int [1:2, 1] 0 1
.. .. ..- attr(*, "dimnames")=List of 2
.. .. .. ..$ : chr [1:2] "essence" "distance"
.. .. .. ..$ : chr "distance"
.. ..- attr(*, "term.labels")= chr "distance"
.. ..- attr(*, "order")= int 1
.. ..- attr(*, "intercept")= int 1
.. ..- attr(*, "response")= int 1
.. ..- attr(*, ".Environment")=<environment: R_GlobalEnv>
.. ..- attr(*, "predvars")= language list(essence, distance)
.. ..- attr(*, "dataClasses")= Named chr [1:2] "numeric" "numeric"
.. .. ..- attr(*, "names")= chr [1:2] "essence" "distance"
$ model :'data.frame': 11 obs. of 2 variables:
..$ essence : int [1:11] 11 20 30 36 16 12 7 8 5 10 ...
..$ distance: int [1:11] 100 200 300 400 150 50 60 70 20 100 ...
..- attr(*, "terms")=Classes 'terms', 'formula' length 3 essence ~ distance
.. .. ..- attr(*, "variables")= language list(essence, distance)
.. .. ..- attr(*, "factors")= int [1:2, 1] 0 1
.. .. .. ..- attr(*, "dimnames")=List of 2
.. .. .. .. ..$ : chr [1:2] "essence" "distance"
.. .. .. .. ..$ : chr "distance"
.. .. ..- attr(*, "term.labels")= chr "distance"
.. .. ..- attr(*, "order")= int 1
.. .. ..- attr(*, "intercept")= int 1
.. .. ..- attr(*, "response")= int 1
.. .. ..- attr(*, ".Environment")=<environment: R_GlobalEnv>
.. .. ..- attr(*, "predvars")= language list(essence, distance)
.. .. ..- attr(*, "dataClasses")= Named chr [1:2] "numeric" "numeric"
.. .. .. ..- attr(*, "names")= chr [1:2] "essence" "distance"
- attr(*, "class")= chr "lm"
NULL
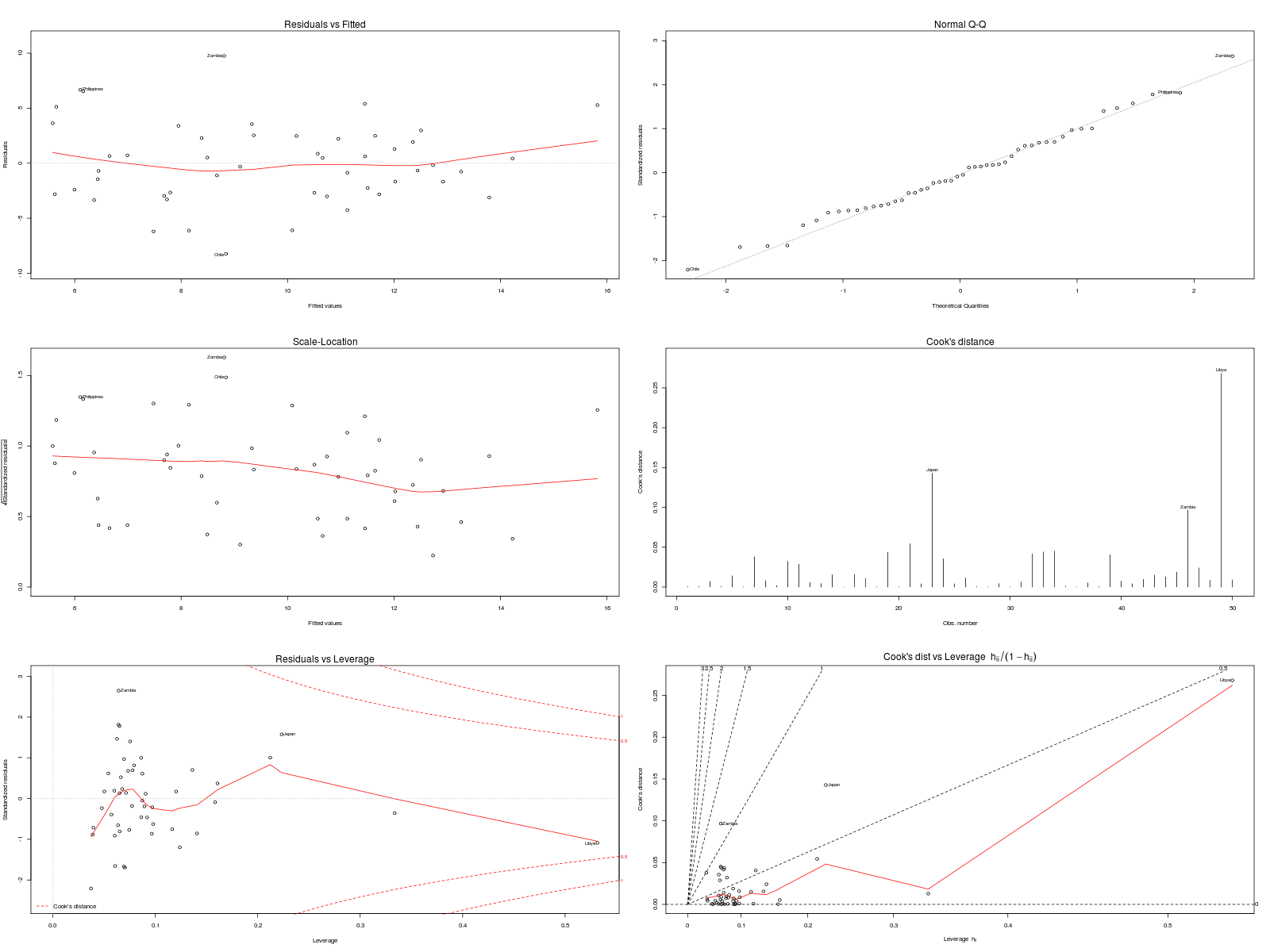
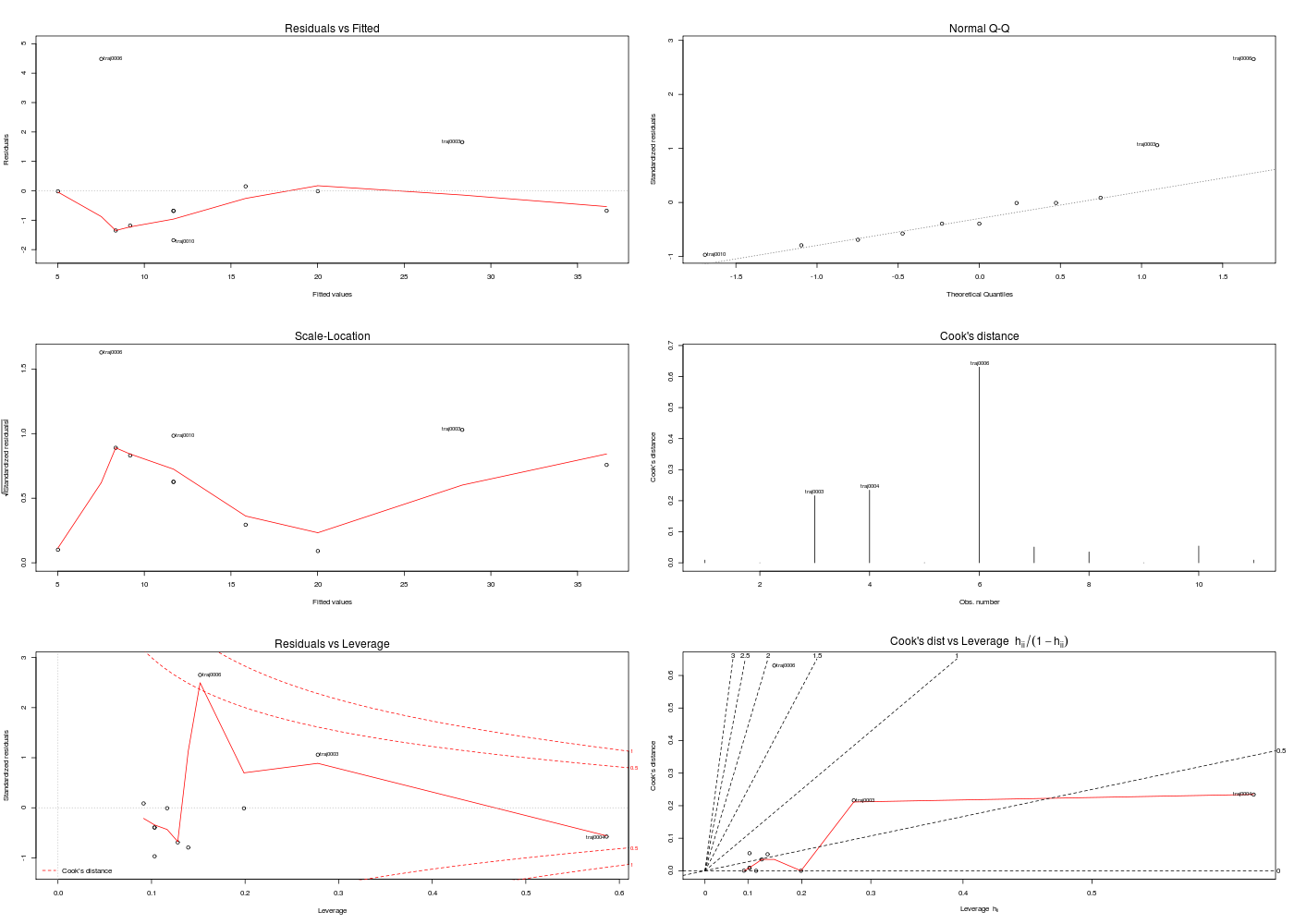
Dans la mesure où un modèle linéaire est [presque] toujours calculable, il faut savoir si le modélisation est significativement non nulle, c'est-à-dire si on peut accepter le modèle. Pour cela, il est d'usage d'utiliser le test de Fisher (de l'analyse de la variance) appliqué au modèle, et ensuite de regarder le coefficient de corrélation linéaire. Il ne faut pas accorder une confiance aveugle à ces tests, qui peuvent être mis en défaut notamment pour de petits échantillons, comme le montre le fameux jeu de données anscombe. On doit donc systématiquement réaliser une analyse des résidus, ce qui peut souvent se réduire à des tracés diagnostics. C'est ce qui explique que R fournit 6 tracés (dont 4 seulement par défaut, repérés ci-dessous par une étoile) pour plot.lm(modele) qui est équivalent à plot(lm(modele)).
| |
x |
y |
| 1 |
* Fitted values |
Residuals |
| 2 |
* Theoretical quantiles |
Standardized residuals |
| 3 |
* Fitted values |
Root of standardized residuals |
| 4 |
Observation number |
Cook's distance |
| 5 |
* Leverage |
Standardized residuals |
| 6 |
Leverage hn |
Cook's distance |
# lecture des données
qansc <- lit.dar("http://www.info.univ-angers.fr/~gh/Datasets/anscombe.dar")
# résumés "à l'aveugle"
cats("les 4 colonnes semblent peu différentes, en résumé")
cols <- paste("Y",1:4,sep="")
mdr <- matrix(nrow=5,ncol=length(cols))
dy <- qansc[,cols]
mdr[1,] <- colMeans( dy )
mdr[2,] <- apply(X=dy,FUN=sd,MARGIN=2)
colnames(mdr) <- cols
row.names(mdr) <- c("Moyennes","Ecarts-type","Statistique F","Rés. normaux","Signif. code")
print(mdr[-3,]) # plus court à écrire que print(mdr[1:2,])
# les différents modèles linéaires
cats("# modèle 1")
print( summary(lm(Y1~X ,data=qansc)) )
cats("# modèle 2")
print( summary(lm(Y2~X ,data=qansc)) )
cats("# modèle 3")
print( summary(lm(Y3~X ,data=qansc)) )
cats("# modèle 4")
print( summary(lm(Y4~X4,data=qansc)) )
## ajoutons la valeur de la F-statistique au tableau des résumés
# une liste de tous les modèles
lstlm <- with(qansc,list(
lm(Y1~X ),
lm(Y2~X ),
lm(Y3~X ),
lm(Y4~X4)
) # fin de liste
) # fin de with
# une fonction pour extraire la statistique F
fstatistic <- function(modele) { return((anova(modele)$"Pr(>F)")[1]) }
# ajout de la statistique F
mdr[3,] <- sapply(X=lstlm,FUN=fstatistic)
# on n'avait pas besoin d'inventer la fonction fstatistic :
mdr2 <- mdr
mdr2[3,] <- sapply(X=lstlm,FUN=function(modele) { return((anova(modele)$"Pr(>F)")[1])})
# print( identical(mdr,mdr2) ) renverrait TRUE
# ajout de la p-value du test de normalité des résidus (shapiro.wilk)
# et son interprétation
mdr2[4,] <- sapply(X=lstlm,FUN=function(modele) { return(shapiro.test(residuals(modele))$p.value) })
mdr2[5,] <- sapply(X=mdr2[4,],FUN=as.sigcode)
# affichage
cats("Tableau résumé")
print(mdr2,quote=FALSE)
# visualisation des résidus
gr("anscres.png")
par(mfrow=c(2,2))
plot(lm(Y1~X,data=qansc),which=1)
plot(lm(Y2~X,data=qansc),which=1)
plot(lm(Y3~X,data=qansc),which=1)
plot(lm(Y4~X4,data=qansc),which=1)
par(mfrow=c(1,1))
dev.off()
les 4 colonnes semblent peu différentes, en résumé
==================================================
Y1 Y2 Y3 Y4
Moyennes 7.500909 7.500909 7.500000 7.500909
Ecarts-type 2.031568 2.031657 2.030424 2.030579
Rés. normaux NA NA NA NA
Signif. code NA NA NA NA
# modèle 1
==========
Call:
lm(formula = Y1 ~ X, data = qansc)
Residuals:
Min 1Q Median 3Q Max
-1.92127 -0.45577 -0.04136 0.70941 1.83882
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.0001 1.1247 2.667 0.02573 *
X 0.5001 0.1179 4.241 0.00217 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.237 on 9 degrees of freedom
Multiple R-squared: 0.6665, Adjusted R-squared: 0.6295
F-statistic: 17.99 on 1 and 9 DF, p-value: 0.00217
# modèle 2
==========
Call:
lm(formula = Y2 ~ X, data = qansc)
Residuals:
Min 1Q Median 3Q Max
-1.9009 -0.7609 0.1291 0.9491 1.2691
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.001 1.125 2.667 0.02576 *
X 0.500 0.118 4.239 0.00218 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.237 on 9 degrees of freedom
Multiple R-squared: 0.6662, Adjusted R-squared: 0.6292
F-statistic: 17.97 on 1 and 9 DF, p-value: 0.002179
# modèle 3
==========
Call:
lm(formula = Y3 ~ X, data = qansc)
Residuals:
Min 1Q Median 3Q Max
-1.1586 -0.6146 -0.2303 0.1540 3.2411
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.0025 1.1245 2.670 0.02562 *
X 0.4997 0.1179 4.239 0.00218 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.236 on 9 degrees of freedom
Multiple R-squared: 0.6663, Adjusted R-squared: 0.6292
F-statistic: 17.97 on 1 and 9 DF, p-value: 0.002176
# modèle 4
==========
Call:
lm(formula = Y4 ~ X4, data = qansc)
Residuals:
Min 1Q Median 3Q Max
-1.751 -0.831 0.000 0.809 1.839
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.0017 1.1239 2.671 0.02559 *
X4 0.4999 0.1178 4.243 0.00216 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.236 on 9 degrees of freedom
Multiple R-squared: 0.6667, Adjusted R-squared: 0.6297
F-statistic: 18 on 1 and 9 DF, p-value: 0.002165
Tableau résumé
==============
Y1 Y2 Y3 Y4
Moyennes 7.50090909090909 7.50090909090909 7.5 7.50090909090909
Ecarts-type 2.03156813592582 2.03165673550162 2.03042360112367 2.0305785113876
Statistique F 0.0021696288730788 0.0021788162369108 0.00217630527922802 0.00216460234719722
Rés. normaux 0.545584685341384 0.0929488137110523 0.00157405546473418 0.780048487911356
Signif. code NS . ** NS
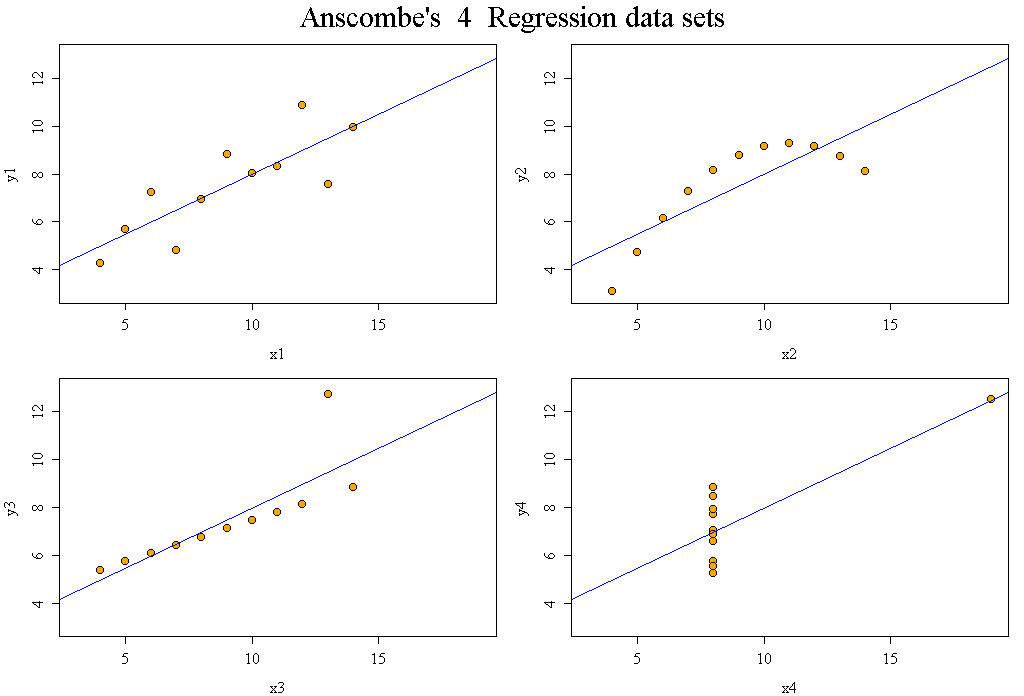
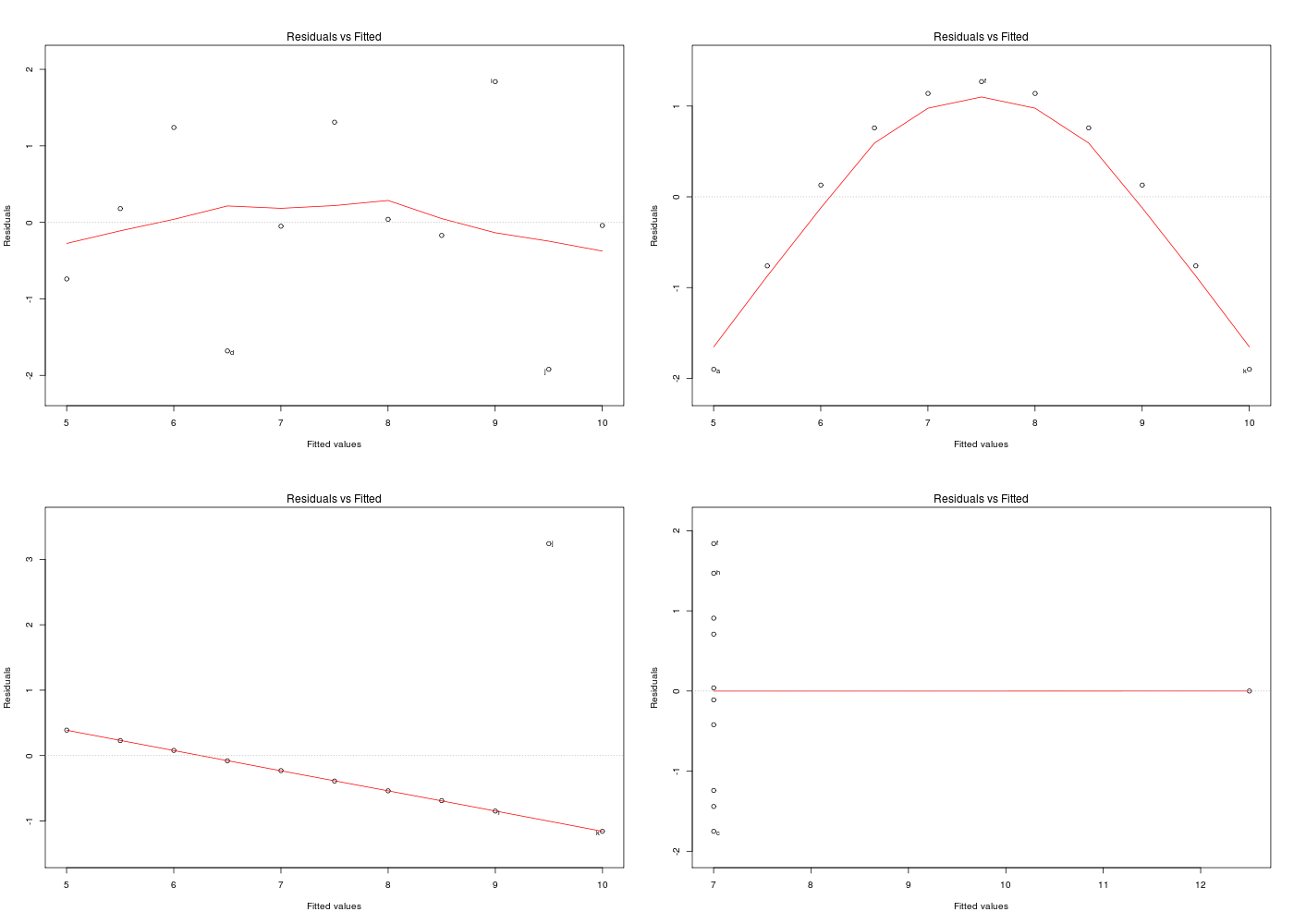
On consultera la page du wiki Anscombe pour plus d'information et on pourra lire la page d'aide associée au jeu de données anscombe du package datasets, aide disponible par help(anscombe) sous R, le tracé étant affiché par example(anscombe).
Une fois le modèle déterminé puis validé, il est possible d'utiliser la fonction générique predict() ou directement la fonction predict.lm() pour appliquer le modèle à de nouvelles données. La seule précaution est qu'il faut utiliser un data frame avec les mêmes noms de variables pour que R soit capable de réaliser les calculs. R permet aussi de calculer les intervalles de confiance pour les coefficients du modèle et pour les valeurs utilisées.
# lecture des données
km <- lit.dar("km.dar")
idx <- order(km$distance)
# modèle linéaire
ml <- lm(essence ~ distance,data=km)
# validité du modèle et analyse des résidus
cats("Modèle linéaire ESSENCE en fonction de DISTANCE")
print( summary(ml) )
cats("anova du modèle","-")
print( anova(ml) )
gr("kmpred1.png")
par(mfrow=c(3,2))
plot(lm(ml),which=1:6)
par(mfrow=c(1,1))
dev.off()
# prédictions
cats("valeurs prédites")
newx <- c(100,250)
# surtout pas
# newy <- predict(ml,newx)
# car cela produit l'erreur
# Erreur dans eval(predvars, data, env) :
# argument numérique 'envir' n'ayant une longueur unitaire
# on construit un nouveau data frame avec le même nom pour x
newxdf <- data.frame(distance=newx)
newy <- predict(ml,newxdf)
print(rbind(newx,newy))
# tracé avec ajout des points prédits et des intervalles de confiance
co <- round(coef(ml),3)
idx <- order(km$distance)
formule <- paste("Consommation = ", 100*co[2]," x distance/100 + ",co[1],sep="")
gr("kmpred2.png")
par(omi=c(0,1,0,0)) # pour avoir plus place à gauche de l'axe
with( km,
plot(essence[idx]~distance[idx],type="p",
pch=19,col="blue",xlim=c(0,800),ylim=c(0,60),
xlab="distance (kilomètres)",ylab="essence (litres)",main=formule
) # fin de plot
) # fin de with
abline(ml,lwd=2,col="black") # droite de régression (moindres carrés ordinaires)
# points pour lesquels on veut une prédiction
points(cbind(newx,newy),cex=1.5,col="red",pch=19)
lines(rep(newx[1],2),c(-10,newy[1]),lty=3,col="blue",lwd=2)
lines(rep(newx[2],2),c(-10,newy[2]),lty=3,col="blue",lwd=2)
lines(c(-50,newx[1]),rep(newy[1],2),lty=3,col="blue",lwd=2)
lines(c(-50,newx[2]),rep(newy[2],2),lty=3,col="blue",lwd=2)
# tracé des intervalles de confiance
grillex <- data.frame(distance=1:800)
icConf <- predict(ml,new=grillex,interval="confidence",level=0.95)
icPred <- predict(ml,new=grillex,interval="prediction",level=0.95)
matlines(grillex,cbind(icConf,icPred[,-1]),lty=c(1,2,2,3,3),col=c("black","red","red","green","green"),lwd=2)
# un légende, c'est utile
legend(
x="topleft",
legend=c("valeurs originales","valeurs prédites","droite MCO","IC conf","IC pred"),
col=c("blue","red","black","red","green"),
pch=c(19,19,NA,NA,NA),
lty=c(0,0,1,3,3),
lwd=c(0,0,2,2,2)
) # fin de legend
dev.off()
Modèle linéaire ESSENCE en fonction de DISTANCE
===============================================
Call:
lm(formula = essence ~ distance, data = km)
Residuals:
Min 1Q Median 3Q Max
-1.6824 -0.9326 -0.6783 0.0686 4.4836
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.350376 0.894150 3.747 0.00458 **
distance 0.083320 0.004985 16.714 4.39e-08 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.835 on 9 degrees of freedom
Multiple R-squared: 0.9688, Adjusted R-squared: 0.9653
F-statistic: 279.4 on 1 and 9 DF, p-value: 4.393e-08
anova du modèle
---------------
Analysis of Variance Table
Response: essence
Df Sum Sq Mean Sq F value Pr(>F)
distance 1 940.61 940.61 279.36 4.393e-08 ***
Residuals 9 30.30 3.37
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
RStudioGD
2
valeurs prédites
================
1 2
newx 100.00000 250.00000
newy 11.68237 24.18035
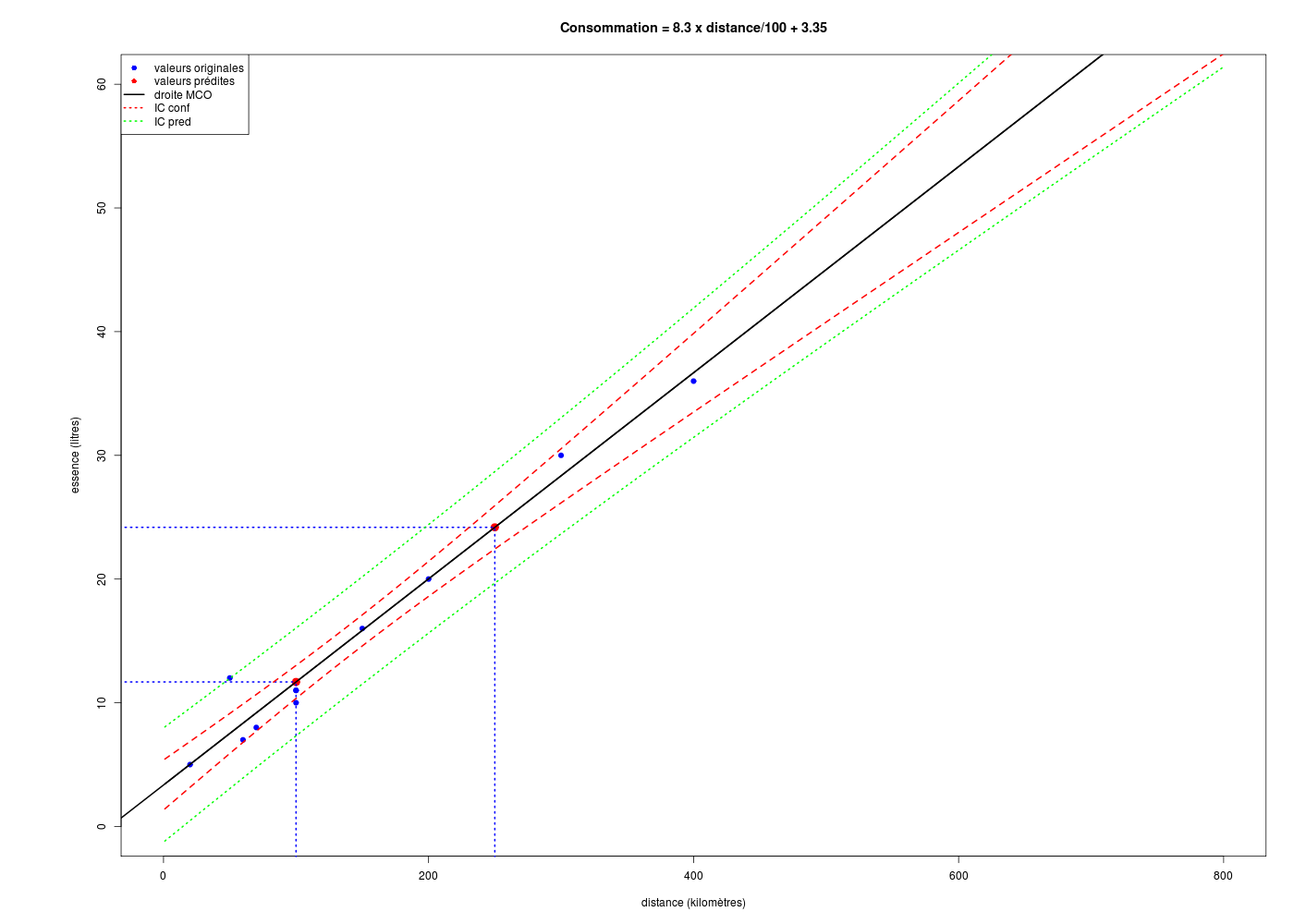
La causalité est une notion extra-statistique et aucun calcul ne permet de savoir si x est une cause et y un effet, puisque les calculs basés sur la corrélation sont symétriques : ρ(x,y)=ρ(y,x). Toutefois ici la distance doit sans doute pouvoir être considérée comme une cause directe de la consommation en essence.
5.2 régression logistique
Prédire le code-sexe d'une personne ou le numéro 0 ou 1 d'un groupe implique de modéliser un résultat binaire, ce que ne peut pas faire une régression linéaire dont le résultat est non borné. Il est usuel d'utiliser une fonction qui varie de 0 à 1 et de choisir un seuil pour prédire une variable binaire. Sous R, cela se fait avec glm() au lieu de lm(). On peut alors utiliser les fonctions génériques comme coef(), predict()...
# lecture des données
pg <- lit.dar("../pg.dar")
# modélisation logistique
rlb <- glm(GROUPE ~ TAILLE, data=pg,family="binomial")
cats("Modèle logistique binaire :")
print(summary(rlb))
idx <- order(pg$TAILLE)
cs <- ifelse(pg$GROUPE==0,"blue","red")
gr("pgpred.png")
par(omi=c(0,0.3,0,0))
plot(
pg$GROUPE[idx]~pg$TAILLE[idx],
ylim=c(0,1),xlim=c(130,200),
col=cs[idx],pch=19,
xlab="TAILLE",ylab="GROUPE",type="p",
main="Régression logistique binaire : modélisation du GROUPE sachant la TAILLE"
) # fin de plot
# prédiction
seuil <- 0.5
newTaille <- data.frame(TAILLE=c(166))
newGrp <- predict(rlb,newdata=newTaille,type="response")
grp <- if (newGrp[1]<0.5) { "groupe 0" } else { "groupe 1" }
cat(" pour TAILLE = ",newTaille[1,1]," valeur prédite ",newGrp[1])
cat(" soit ",grp," (au seuil a priori de ",seuil,") \n",sep="")
# point à prédire
points(newTaille[1,1],newGrp[1],pch=19,col="darkgreen",cex=1.5)
lines(rep(newTaille[1,1],2),c(-10,newGrp[1]),lty=3,col="darkgreen",lwd=2)
lines(c(-50,newTaille[1,1]),rep(newGrp[1],2),lty=3,col="darkgreen",lwd=2)
# fonction logistique et tracé
co <- coef(rlb)
logis <- function(x) { # x est l'TAILLE
comblin <- co[1] + co[2]*x
lexpo <- exp( comblin )
pidex <- lexpo / (1 + lexpo )
return(pidex)
} # fin de fonction logis
tailles <- 100:200
groupe <- logis(tailles)
lines(groupe~tailles,type="l")
# on aurait aussi pu écrire :
tailles <- data.frame(TAILLE=100:200)
groupe <- predict(rlb,newdata=tailles,type="response")
# lines(groupe~tailles$TAILLE,type="l")
abline(h=0.5,lty=3,col="blue")
text(x=135,y=0.55,labels="seuil a priori")
legend(
legend=c("groupe 0","groupe 1","point à prédire","fonction logistique","seuil"),
x="bottomright",
col=c("blue","red","darkgreen","black","blue"),
pch=c(rep(19,3),NA,NA),
lty=c(rep(0,3),1,3)
) # fin de légende
dev.off()
# qualité du modèle
va <- auroc(dataFrame=pgg,nomCible="GROUPE",lesVars="TAILLE",print=FALSE)
cat(" AUROC = ",va[1],"\n")
Modèle logistique binaire :
===========================
Call:
glm(formula = GROUPE ~ TAILLE, family = "binomial", data = pg)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.1225 -0.2589 0.1087 0.2728 1.9168
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -27.21029 8.95762 -3.038 0.00238 **
TAILLE 0.18118 0.05893 3.074 0.00211 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 38.191 on 29 degrees of freedom
Residual deviance: 10.895 on 28 degrees of freedom
AIC: 14.895
Number of Fisher Scoring iterations: 6
pour TAILLE = 166 valeur prédite 0.9461448 soit groupe 1 (au seuil a priori de 0.5)
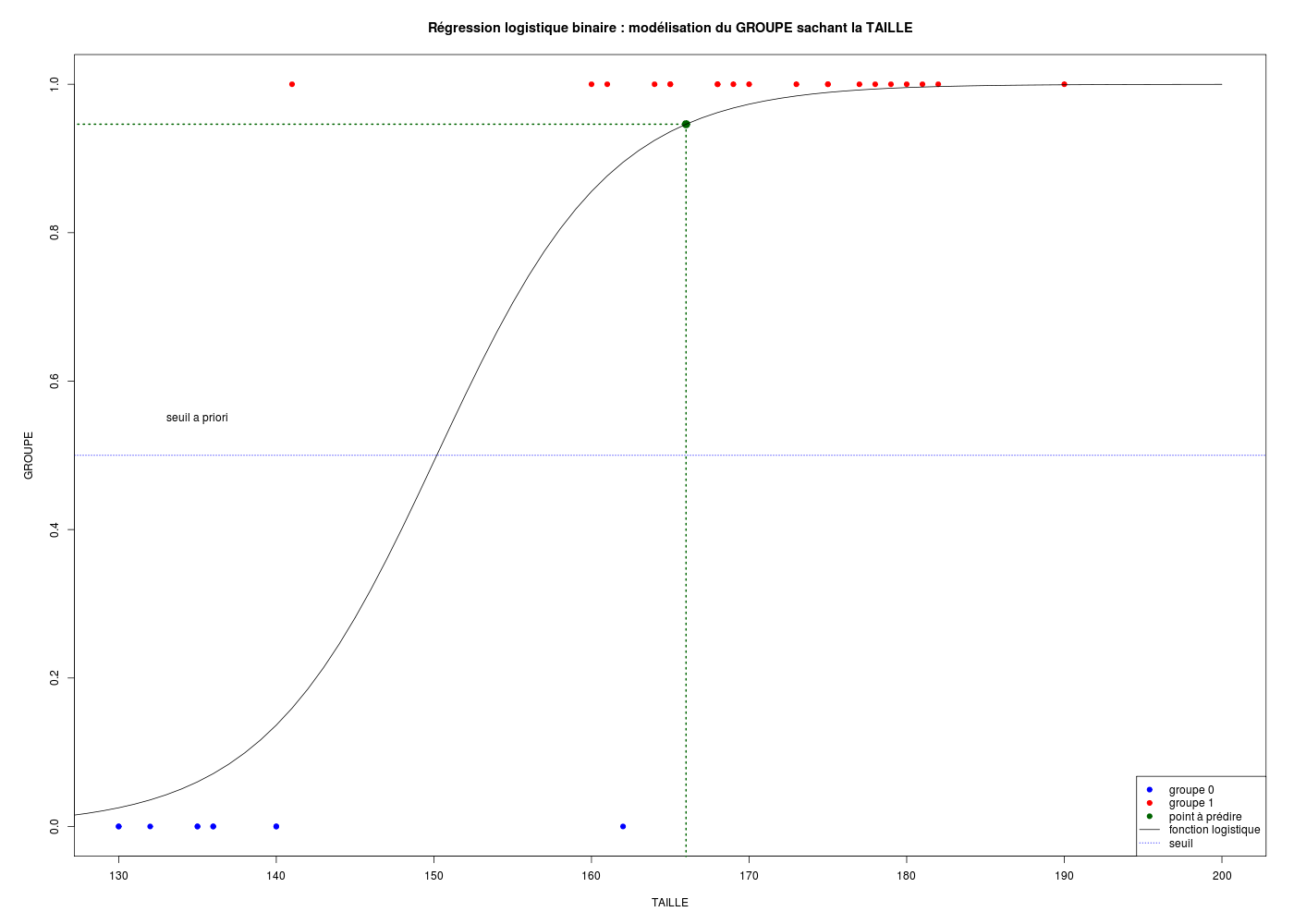
La qualité d'un modèle logistique peut être appréciée via l'aire sous la courbe ou AUC ou
AUROC. Pour la modélisation du GROUPE en fonction de la taille, l'AUROC vaut 0,95 le modèle est un bon modèle. Par contre pour la modélisation du SEXE en fonction de l'AGE, l'AUROC vaut 0,35 et il s'agit donc d'un "très mauvais" modèle, choisir le code SEXE au hasard donnerait de meilleurs résultats !
# lecture des données
elf <- lit.dar("http://www.info.univ-angers.fr/~gh/Datasets/elf.dar")
# modélisation
rlb <- glm(SEXE ~ AGE, data=elf,family="binomial")
cats("Modèle logistique binaire :")
print(summary(rlb))
idx <- order(elf$AGE)
cs <- ifelse(elf$SEXE==0,"blue","red")
plot(
elf$SEXE[idx]~elf$AGE[idx],
ylim=c(0,1),xlim=c(0,100),
col=cs[idx],pch=19,
xlab="AGE",ylab="SEXE",
main="Régression logistique binaire : prédiction du SEXE sachant l'AGE"
) # fin de plot
# prédiction
seuil <- 0.5
newAge <- data.frame(AGE=c(50))
newSexe <- predict(rlb,newdata=newAge,type="response")
sexp <- if (newSexe[1]<0.5) { "homme" } else { "femme" }
cat(" pour AGE = ",newAge[1,1]," valeur prédite ",newSexe[1])
cat(" soit ",sexp," (au seuil a priori de ",seuil,") \n",sep="")
sexs <- predict(rlb,data=elf,type="response")
lines(sexs~elf$AGE,type="l")
# qualité du modèle
va <- auroc(dataFrame=elf,nomCible="SEXE",lesVars="AGE",print=FALSE)
cat(" AUROC = ",va[1],"\n")
Modèle logistique binaire :
===========================
Call:
glm(formula = SEXE ~ AGE, family = "binomial", data = elf)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.4731 -1.4278 0.9156 0.9363 0.9784
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.707316 0.480871 1.471 0.141
AGE -0.002886 0.011986 -0.241 0.810
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 128.62 on 98 degrees of freedom
Residual deviance: 128.56 on 97 degrees of freedom
AIC: 132.56
Number of Fisher Scoring iterations: 4
pour AGE = 50 valeur prédite 0.6371456 soit femme (au seuil a priori de 0.5)
AUROC = 0.3493156
5.3 analyse de la variance
Sur les liens entre régression linéaire, corrélation et analyse de la variance, voir la solution de l' exercice 3 de mon cours de niveau 2 à l'école doctorale.
Un bon manuel de cours sur ce sujet est nommé le modèle linéaire par l'exemple On peut le télécharger à l'adresse modlin (copie locale) Les formules présentées sont appliquées avec divers logiciels dont R dans l'ouvrage modlin4bis (copie locale).
Voici, sans explication (c'est volontaire) mais avec les résultats et les graphiques, la comparaison de l'age des hommes et des femmes dans le dossier ELF.
## lecture des données
elf <- lit.dar("http://www.info.univ-angers.fr/~gh/Datasets/elf.dar")
sexe <- elf$SEXE
sexef <- factor(elf$SEXE,labels=c("Homme","Femme"))
age <- elf$AGE
## 1. analyse séparée des variables AGE et SEXE
# en R classique
print(summary(age))
hist(age)
print(summary(sexef))
barplot(table(sexef))
# avec les fonctions (gH)
decritQT(
titreQT="AGE (dossier ELF)",
nomVar=elf$AGE,
unite="ans",
graphique=TRUE
) # fin de decriQT
decritQLf(
titreQL="SEXE (dossier ELF)",
nomFact=sexef,
graphique=TRUE,
ordreModalites=TRUE,
testequi=TRUE
) # fin de decriQLf
## 2. analyse conjointe des variables AGE et SEXE
# en R classique
ml <- lm(age ~ sexef)
print(summary(ml))
print(anova(ml))
boxplot(age~sexef)
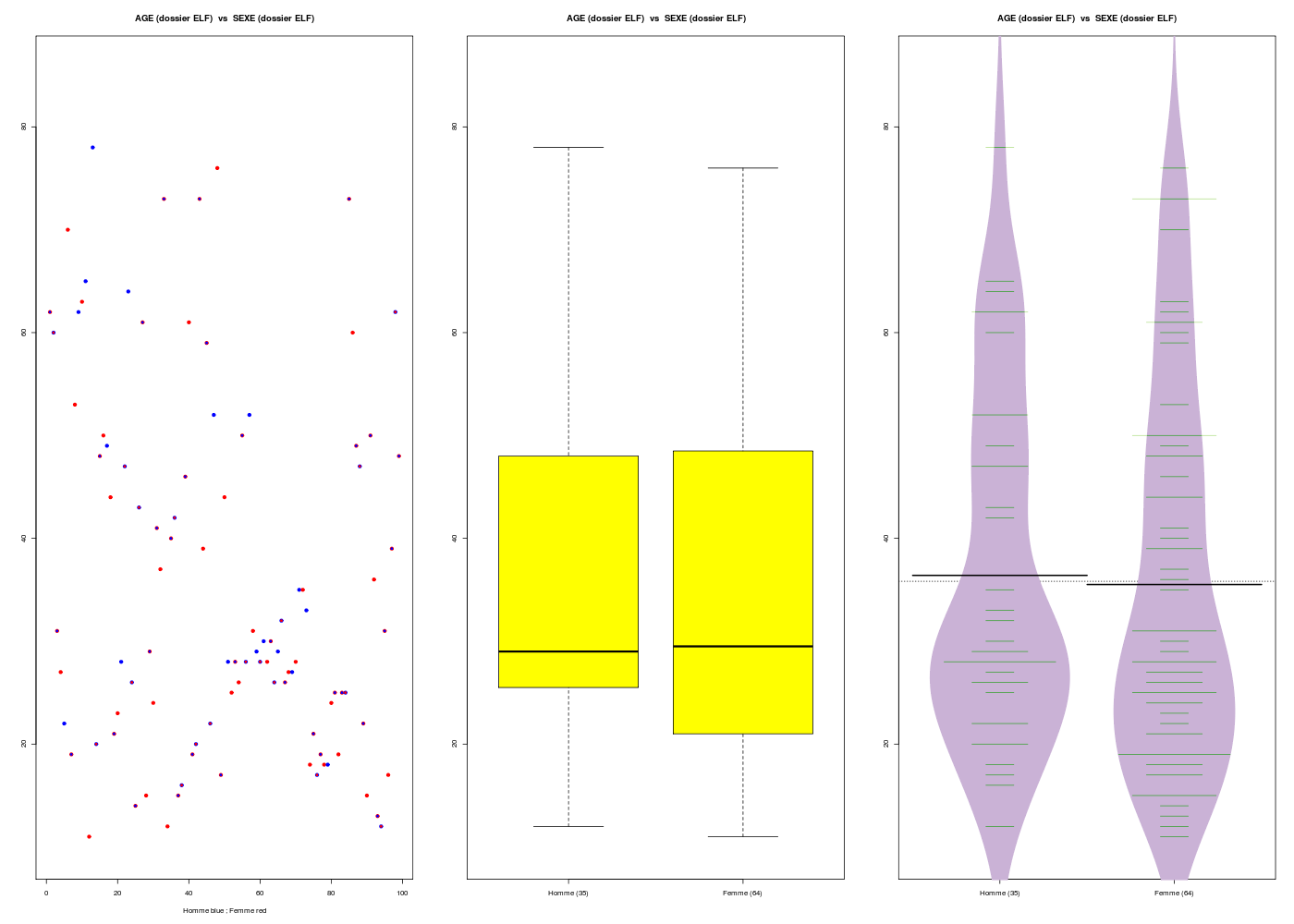
# avec les fonctions (gH)
decritQTparFacteur(
titreQT="AGE (dossier ELF)",
nomVarQT=age,
unite="ans",
titreQL="SEXE (dossier ELF)",
nomVarQL=sexe,
labels="Homme Femme",
graphique=TRUE,
beanp=TRUE
) # fin de decritQTparFacteur
Min. 1st Qu. Median Mean 3rd Qu. Max.
11.00 22.00 29.00 35.83 48.50 78.00
Homme Femme
35 64
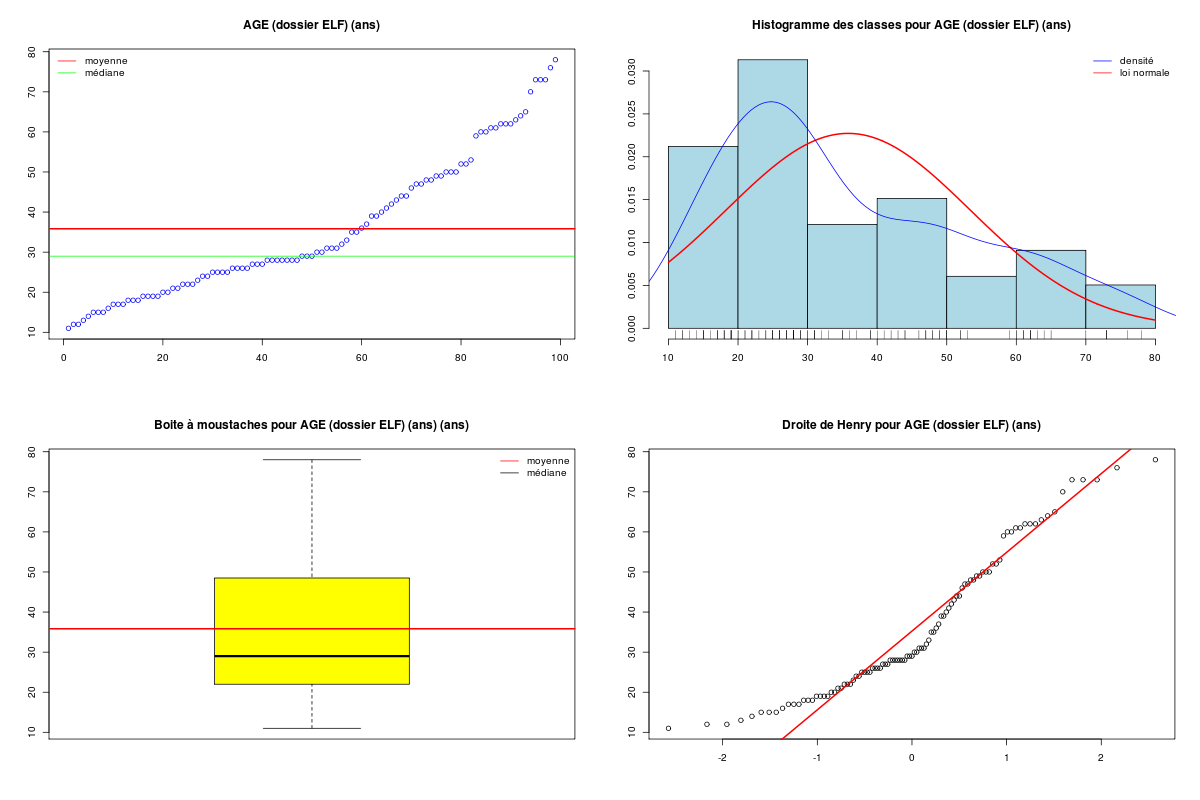
DESCRIPTION STATISTIQUE DE LA VARIABLE AGE (dossier ELF)
Taille 99 individus
Moyenne 35.8283 ans
Ecart-type 17.5529 ans
Coef. de variation 49 %
1er Quartile 22.0000 ans
Mediane 29.0000 ans
3eme Quartile 48.5000 ans
iqr absolu 26.5000 ans
iqr relatif 91.0000 %
Minimum 11 ans
Maximum 78 ans
Tracé tige et feuilles
The decimal point is 1 digit(s) to the right of the |
1 | 1223455567778889999
2 | 0011222344555566667778888888999
3 | 0011123556799
4 | 0123446778899
5 | 0002239
6 | 0011222345
7 | 033368
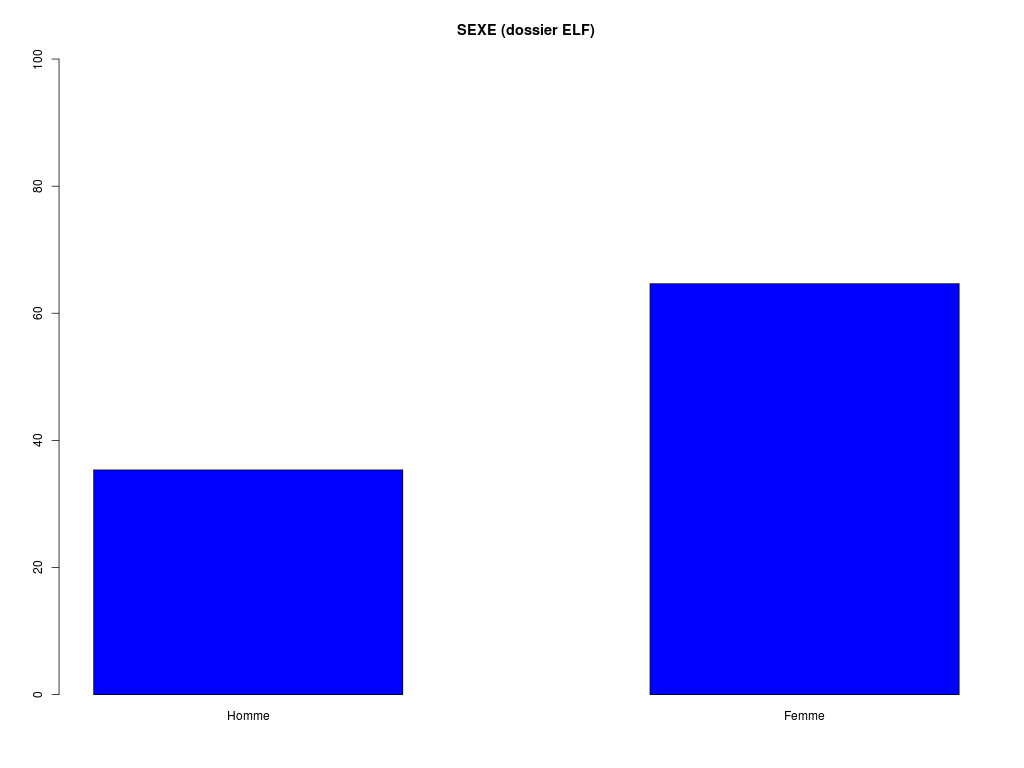
TRI A PLAT DE : SEXE (dossier ELF) (ordre des modalités)
Homme Femme Total
Effectif 35 64 99
Cumul Effectif 35 99 99
Frequence (en %) 35 65 100
Cumul fréquences 35 100 100
VARIABLE : SEXE (dossier ELF) (par fréquence décroissante)
Femme Homme Total
Effectif 64 35 99
Cumul Effectif 35 99 99
Frequence (en %) 65 35 100
Cumul fréquences 65 100 100
[1] "Homme" "Femme"
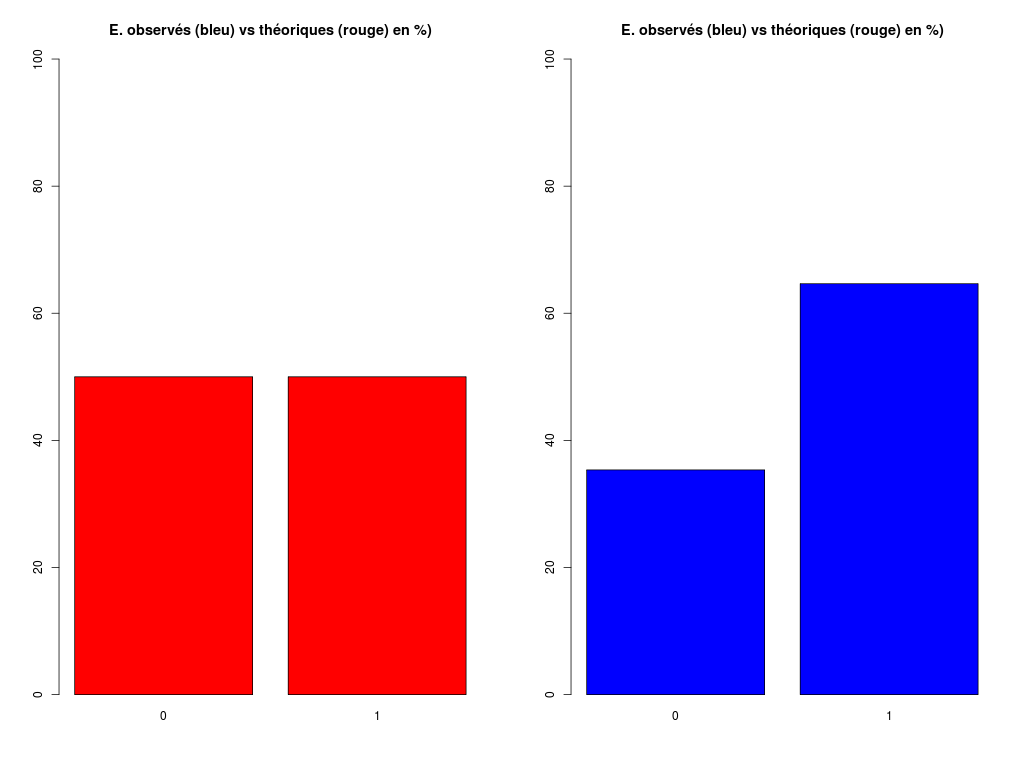
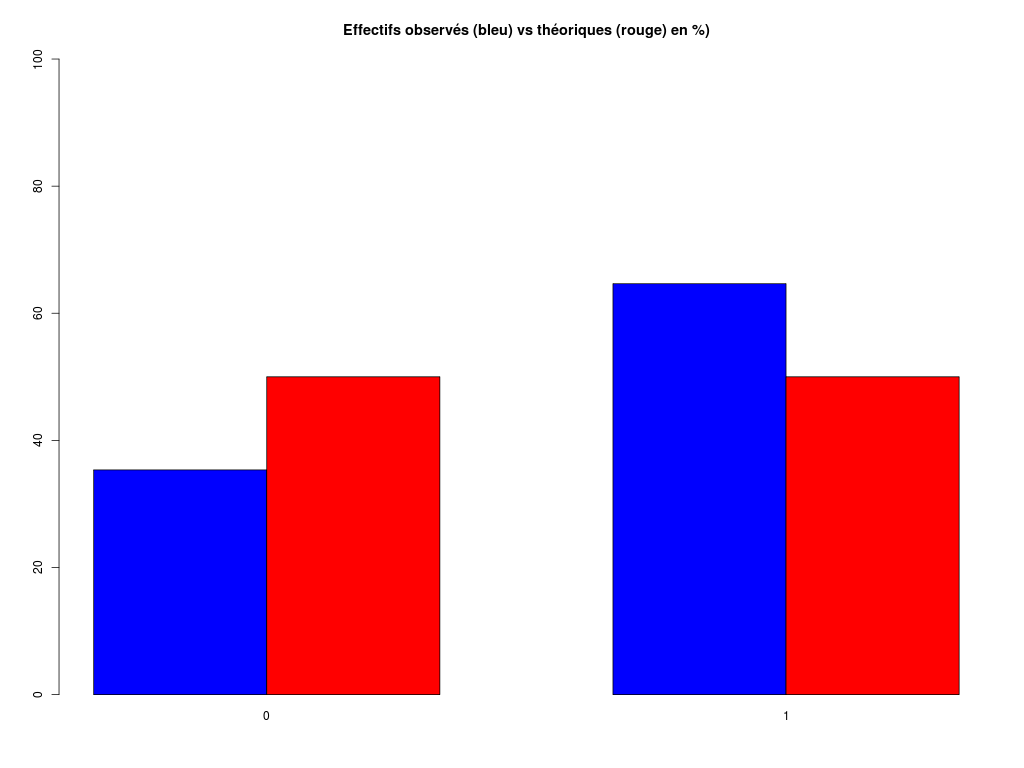
CALCUL DU CHI-DEUX D'ADEQUATION
Valeurs théoriques 49.5 49.5
Valeurs observées 35 64
Valeur du chi-deux 8.494949
Chi-deux max (table) à 5 % 3.841459 pour 1 degrés de liberté ; p-value 0.003561337
décision : au seuil de 5 % on peut rejeter l'hypothèse
que les données observées correspondent aux valeurs théoriques.
Contributions au chi-deux
Ind. The Obs Dif Cntr Pct Cumul
1 49.5 35 14.5 4.247475 50 4.247475
2 49.5 64 -14.5 4.247475 50 8.494949
Call:
lm(formula = age ~ sexef)
Residuals:
Min 1Q Median 3Q Max
-24.516 -13.958 -6.516 12.542 41.600
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 36.4000 2.9814 12.209 <2e-16 ***
sexefFemme -0.8844 3.7080 -0.239 0.812
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 17.64 on 97 degrees of freedom
Multiple R-squared: 0.0005861, Adjusted R-squared: -0.009717
F-statistic: 0.05688 on 1 and 97 DF, p-value: 0.812
Analysis of Variance Table
Response: age
Df Sum Sq Mean Sq F value Pr(>F)
sexef 1 17.7 17.696 0.0569 0.812
Residuals 97 30176.4 311.097
VARIABLE QT AGE (dossier ELF) ,unit=ans
VARIABLE QL SEXE (dossier ELF) labels : Homme Femme
N Moy Unite Ect Cdv Q1 Med Q3 EIQ Min Max
Global 99 35.828 ans 17.464 49 22.000 29.000 48.500 26.500 11.000 78.000
Homme 35 36.400 ans 16.650 46 25.500 29.000 48.000 22.500 12.000 78.000
Femme 64 35.516 ans 17.886 50 21.000 29.500 48.250 27.250 11.000 76.000
Analysis of Variance Table
Response: nomVarQT
Df Sum Sq Mean Sq F value Pr(>F)
ql 1 17.7 17.696 0.0569 0.812
Residuals 97 30176.4 311.097
Kruskal-Wallis rank sum test
data: nomVarQT by ql
Kruskal-Wallis chi-squared = 0.3016, df = 1, p-value = 0.5829
6. Exemples de tests statistiques

|
Qu'est-ce qu'un test statistique ?
Quels sont les principaux tests disponibles sous R ?
Y a-t-il des représentations graphiques associées ?
Combien y a-t-il de pages dans l'ouvrage Comprendre et réaliser les tests statistiques à l'aide de R de G. MILLOT ?
Qu'est-ce qu'un test t ? Que peut-on déduire d'un calcul fait avec la fonction t.test() ?
|
Un test statistique est une procédure complexe qui part d'une hypothèse-métier pour aboutir au rejet ou au non rejet d'une hypothèse dite nulle, pour un certain risque [de se tromper], qui s'accompagne d'une phrase de conclusion comme il n'y pas de différence significative au seuil choisi. Entre ces deux extrêmes, il y a un certain nombres d'opérations techniques, comme le choix du test en fonction de la taille et de la normalité des données, la modélisation probabiliste du test, la vérification de son application, le choix de la bilatéralité ou non, etc.
Pour les «singes savants», on applique une fonction qui se termine par .test() à des données et on est content si p est inférieur à 0,05.
Pour une présentation plus complète, nous renvoyons à notre page officielle sur les tests.
Il y a une trentaine de tests disponibles dans le package stats. En voici la liste :
ansari.test bartlett.test
binom.test Box.test
chisq.test cor.test
fisher.test fligner.test
friedman.test kruskal.test
ks.test mantelhaen.test
mauchly.test mcnemar.test
mood.test oneway.test
pairwise.prop.test pairwise.t.test
pairwise.wilcox.test poisson.test
power.anova.test power.prop.test
power.t.test PP.test
prop.test prop.trend.test
quade.test shapiro.test
t.test var.test
wilcox.test
De nombreux autres packages contiennent aussi des tests et il n'est donc pas simple de tous les connaitre, sachant que connaitre un test ne signifie pas juste connaitre son nom et la liste de ses paramètres.
Il y a parfois des représentations graphiques associées, comme la droite de Henry ou les boxplots à encoche, mais ce n'est pas forcément le cas de tous les tests. De plus ces représentations ne sont que des aides à la compréhension...
Le «gros pavé» de G. Millot est un ouvrage en français d'environ 700 pages dédiés aux tests usuels de R. C'est un bon ouvrage qui fournit une présentation de R, des rappels probabilistes et statistiques, des exemples détaillés. Nous conseillons sa lecture.
Comme son nom l'indique, le test t fourni par la fonction t.test() de R permet d'effectuer des tests t de Student et de Welsch, qui permet de comparer les moyennes de deux séries de données, pour des variances égales ou inégales. Au passage, il calcule des intervalles de confiance et permet de tester l'égalité à une moyenne de référence. Il a une option pour des données appariées.
7. Analyse de données : ACP, AFC et CAH
Qu'est-ce que l'Analyse des Donnéees au sens de JPB ?

Jean-Paul Benzécri, octobre 2006, INA-PG
(photo Guiseppe Giordano-Univ. Salerne)
Comment réalise-t-on une ACP, une AFC et une CAH avec R ?
Y a-t-il des représentations graphiques associées, des packages spécifiques, des ouvrages dédiés en R ?
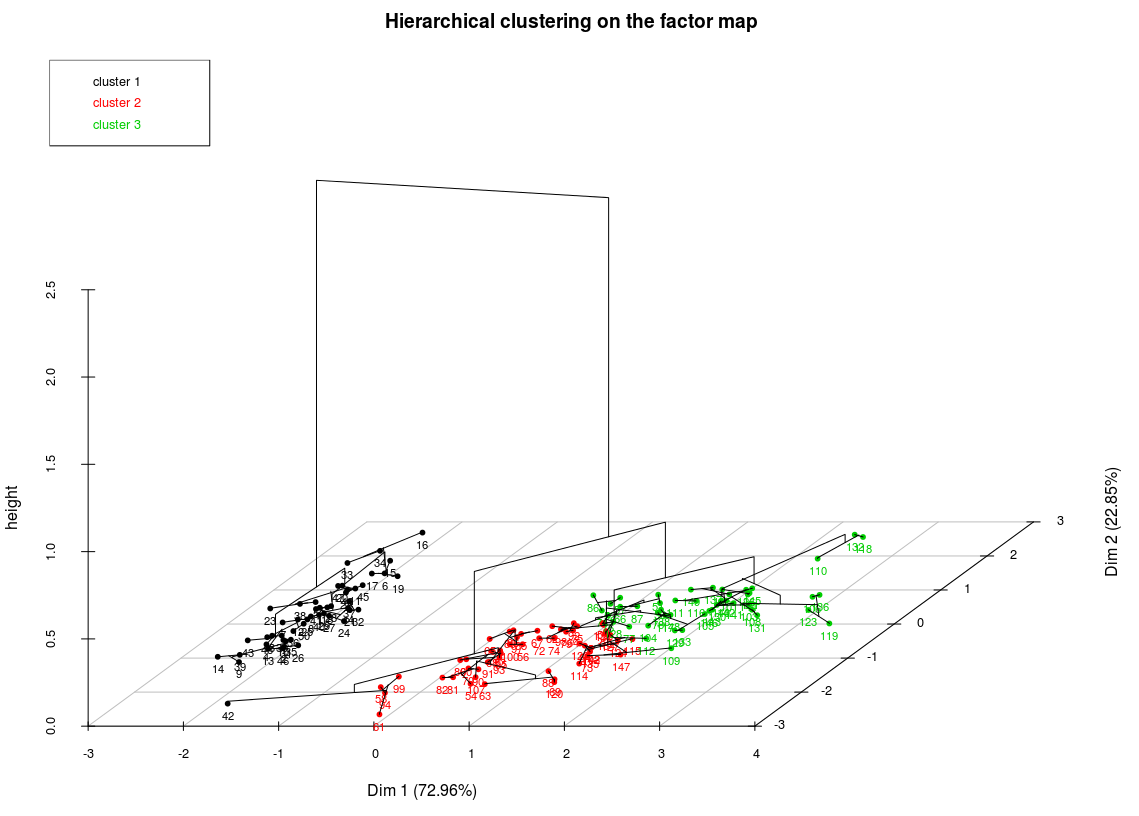
L'analyse des données (ou AD) au sens de JPB est un ensemble de méthodes de statistiques descriptives multidimensionnelles dont les plus connues sont les AFC (analyses factorielles des correspondances), les ACP (analyses en composantes principales) et les CAH (classifications ascendantes hiérarchiques).
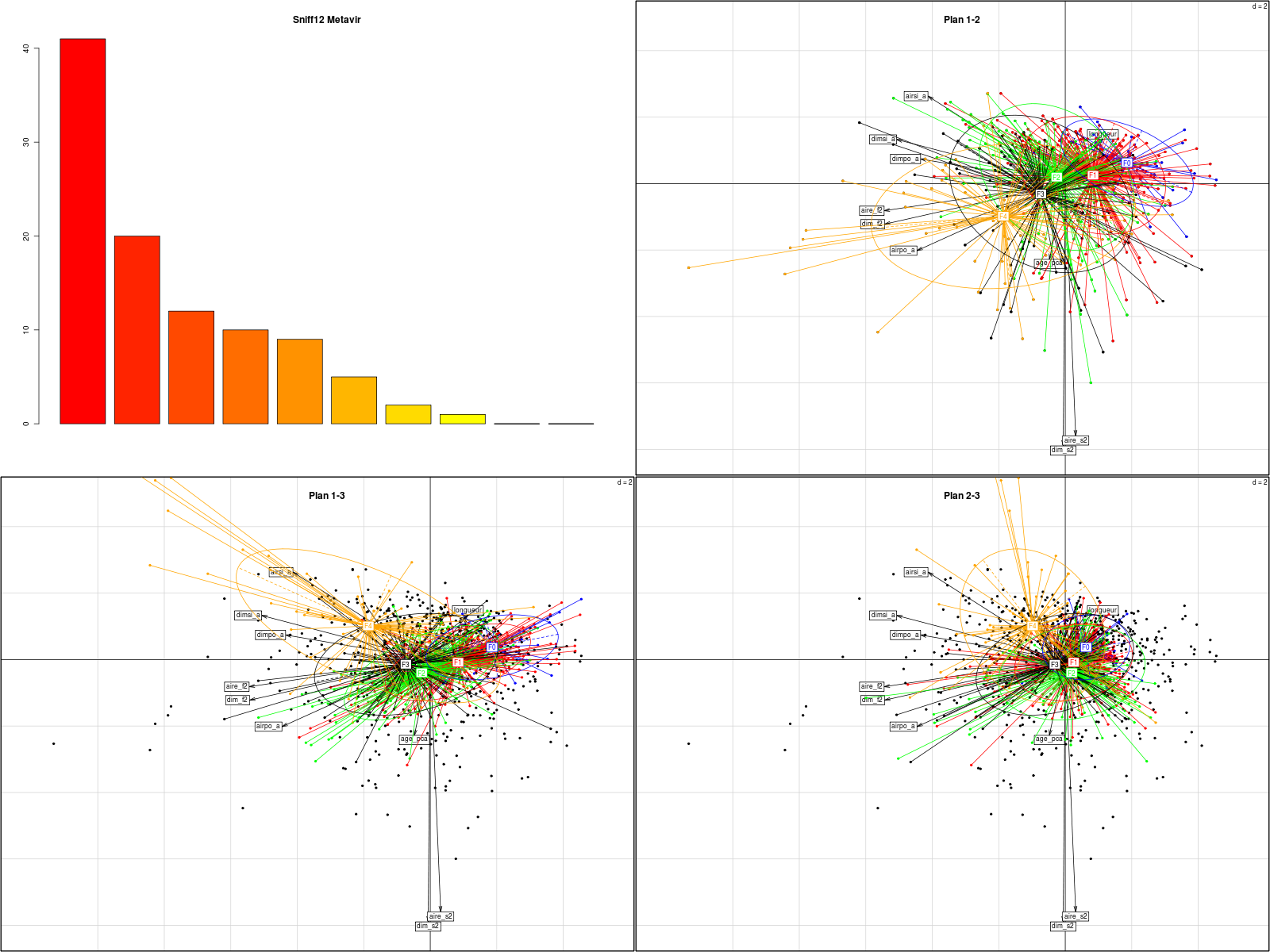
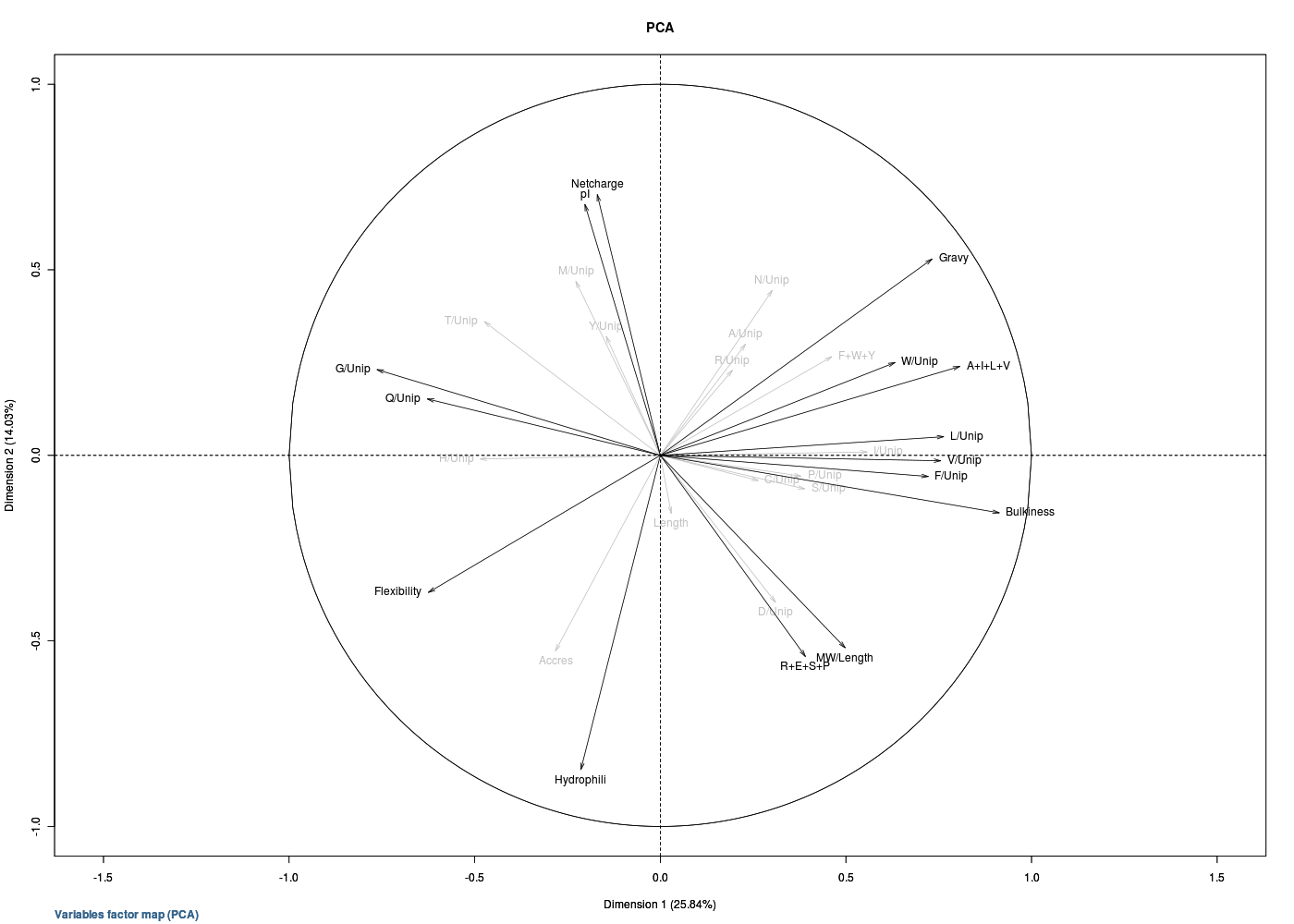
Il y a bien sûr des représentations graphiques associées comme par exemple le «cercle des corrélations», les «plans factoriels» auxquels on peut adjoindre des ellipses de confiance, les «dendrogrammes»...
Les fonctions prcomp() et princomp() du package stats sont en général insuffisantes et il est souvent préférables de recourir aux fonctions des packages FactoMineR et ade4 pour ne citer que des packages développés par des français. On se rendra compte du nombre de méthodes associées et des variantes qui existent un peu partout en consultant les Task Views nommées Multivariate, Cluster et Environmetrics si on se restreint aux principales vues liées à ce type d'analyses.
Comme pour les tests, réaliser une AD est simple puisqu'il suffit d'appeler une fonction. Par contre le travail de "dépouillement" des informations, comme le choix du nombre d'axes à retenir, la recherche des meilleures contributions aux axes et l'interprétation des axes est un travail long (mais passionnant). Pour les personnes pressées de voir R en action pour l'AD, on fera un copier/coller des commandes suivantes :
# démonstration d'analyse des données avec FactorMiner
library(FactoMineR)
example(PCA) # ACP : Analyse en Composantes Principales
example(CA) # AFC : Analyse Factorielle des Correspondances
example(MCA) # ACM : Analyse Factorielle des Correspondances Multiples
example(HCPC) # CAH : Classification Ascendante Hiérarchiques
detach(name="package:FactoMineR")
# démonstration d'analyse des données avec ade4
library(ade4)
example(dudi.pca) # ACP : Analyse en Composantes Principales
example(dudi.coa) # AFC : Analyse Factorielle des Correspondances
example(dudi.acm) # ACM : Analyse Factorielle des Correspondances Multiples
FactoMineR dispose d'un site, d'un ouvrage en français, d'un ouvrage en anglais et même de vidéos. De plus FactoMineR fournit un plug-in pour Rcmdr. Par contre ade4 dispose d'un site beaucoup plus fourni mais pas d'ouvrage, à notre connaissance.
 
8. Export de résultats en PDF avec Sweave
Comment produire rapidement un document PDF des résultats et graphiques ?
Que sont Markdown et Sweave ? et knitr ?
Une fois les calculs mis au point avec R, il est d'usage de les intégrer dans un document, un rapport, un article... Il est clair qu'une technique comme le copier/coller peut se révéler fastidieuse et source d'erreur pour inclure les données et les graphiques. Markdown et Sweave sont deux solutions techniques pour éviter le copier/coller et pour automatiser l'inclusion des résultats et des graphiques. Markdown est un langage à marqueurs léger. Il est à noter que Rcmdr fournit et propose de sauvegarder le code Markdown correspondant aux commandes effectuées via les clics-souris dans les menus.
Sweave est une solution «plus professionnelle» basée sur LaTeX et c'est la solution que nous recommandons, car elle fournit des résultats propres et reproductibles. De plus, Sweave est intégré à Rstudio.
Sur le site officiel de Sweave on trouve plusieurs fichiers de démonstrations, un manuel et une FAQ. En français, une documentation intéressante et détaillée est le http://pbil.univ-lyon1.fr/R/pdf/tdr78.pdf de J. R. Lobry (copie locale). knitr généralise Sweave et c'est la solution que nous conseillons après comparaison des deux solutions (mais il faut aussi connaitre LaTeX).
Voici comment cela fonctionne avec Rstudio : on écrit un fichier de type .rnw comme par exemple demosweave.rnw puis on utilise l'icone Compile PDF. Rstudio vient alors créer le fichier demosweave.tex en exécutant R et en intégrant les sorties éventuelles (calculs ou graphiques) pour chaque «chunk» débuté par << et terminé par @. Si tout est bien configuré, Rstudio compile via pdflatex le fichier produit et affiche le résultat. Magnifique !
Voici les fichiers utilisés, sachant que notre mise en page LaTeX est dans dctgh.tex et que nous avons écrit une fonction demoSw() que nous avons testée en-dehors de Sweave, pour plus de souplesse. Cette fonction est définie dans poursweave.r. Le fichier PDF obtenu est demosweave1.pdf si la variable dos vaut iris et demosweave2.pdf si la variable dos vaut elf, mais bien sûr, il faut connaitre LaTeX, ce qui est une autre histoire...
demosweave1.rnw demosweave1.tex demosweave2.rnw demosweave2.tex dctgh.tex poursweave.r
9. Non présentation (!) du package stats
Que contient le package stats ? Quelles en sont les fonctions les plus importantes ?
Hélas, le package stats contient environ 500 objets, il est difficile en dix minutes d'en faire le tour...
On peut quand même distinguer des fonctions "classiques" de calcul et de probabilités, des fonctions pour les tests statistiques usuels, des fonctions d'affichage pour les différents modèles et des fonctions de tracé.
Code-source php de cette page ; code javascript utilisé. Retour à la page principale du cours.
|
 Retour à la page principale de
(gH)
Retour à la page principale de
(gH)