|
Solutions pour la séance numéro 4 (énoncés)
|
 Retour à la page principale de
(gH)
Retour à la page principale de
(gH)
Module de Biostatistiques,
partie 1
Ecole Doctorale Biologie Santé
gilles.hunault "at" univ-angers.fr
Solutions pour la séance numéro 4 (énoncés)
La densité d'une loi probabiliste discrète, c'est la probabilité pour la valeur considérée. La répartition, c'est le cumul des probabilités jusqu'à la valeur considérée. Avec des formules : la densité en a est p("X=a") ; la répartition en a est F(a) = p("X≤a"). On emploie souvent le terme de loi au lieu de distribution et de fonction de répartition au lieu de répartition. Le terme densité cumulée n'est en général pas utilisé en France. Par contre en anglais, on parle de density function ou df et de cumulative density function (distribution function) ou cdf. Il se justifie par le fait que p("X≤a") = p("X=0") + p("X=1") +... p("X=a") pour une loi discrète.
Pour plus de détails, consulter le wiki français puis anglais sur
Pour une loi donnée, sous R, le préfixe d donne la densité, le préfixe p la répartition, le préfixe q les quantiles (fonction réciproque de la répartition) et le préfixe r fournit un tirage aléatoire. Voici un exemple pour la loi binomiale avec les fonctions dbinom, pbinom, qbinom et rbinom :
> dbinom(0,15,0.2) 0.03518437 > dbinom(1,15,0.2) 0.1319414 > dbinom(0:1,15,0.2) 0.03518437 0.13194140 > dbinom(0,15,0.2)+dbinom(1,15,0.2) 0.1671258 > pbinom(1,15,0.2) 0.1671258 > qbinom(0.1671257,15,0.2) 1 > rbinom(10,15,0.2) 6 2 2 3 1 4 3 2 3 4En particulier, si on veut des nombres "aléatoires", on peut utiliser runif qui fournit des nombres compris entre 0 et 1 (par défaut, mais on peut ajouter des paramètres min et max) uniforméments répartis :
> runif(1) # un seul nombre aléatoire 0.3636898 > runif(1) # et un autre 0.626016 > runif(5) # cinq nombres aléatoires 0.95392210 0.06394494 0.26294750 0.76512871 0.82309546 > runif(5,1,10) # cinq autres, entre 1 et 10 8.295080 5.770958 1.441638 5.014874 8.647515 > v <- runif(5,1,10) # cinq nombres aléatoires > print(v) # affichage 9.783909 1.756172 4.980089 5.384019 9.504967 > print(round(v)) # affichage en arrondi 10 2 5 5 10La fonction approx calcule les valeurs vb du modèle binomial B(n,p) pour toutes les valeurs xb possibles (de 0 à n) et les trace en rouge par plot. Elle calcule ensuite les valeurs vp de la loi de Poisson P(lambda) de même moyenne (lambda = np) pour les valeurs xp de 0 à 3n et les trace en bleu par points. Enfin, la fonction calcule les valeurs vn de la loi normale de même moyenne et de même écart-type pour xn de -nbp*n à nbp*n où nbp désigne le nombre de points (soit 100 ici) et les trace en noir par points. Cette fonction permet de voir la proximité des valeurs pour les différentes lois. En voici quatre exemples.
Le troisième paramètre de la fonction, nommé lx, est égal à la chaine vide par défaut. Il permet de n'afficher la partie du tracé correspondant à la plage de variation spécifiée pour x dans lx. Ainsi les deux tracés suivant sont obtenus respectivement par approx(1500,0.001) et approx(1500,0.001,c(0,20)).
L'hypothèse d'équiprobabilité consiste à poser que la densité (de probabilité) est constante. Le modèle théorique est nommé loi uniforme discrète. Les fréquences théoriques sont alors toutes égales : il suffit de diviser l'effectif total par le nombre de valeurs pour obtenir la fréquence théorique commune. La probabilité théorique commune s'obtient de même par 1/n où n est le nombre de valeurs.
Avec 670 patients et trois grades, chaque grade a, sous hypothèse d'équiprobabilité, une fréquence de 670/3 soit 223,33. On pourra utiliser notre page http://www.info.univ-angers.fr/~gh/vitrine/Democgi/loisStatp.htm avec les paramètres U 1 3 670 pour le vérifier. Avec R, on peut écrire rep( 670/3, 3) ou rep( round(670/3), 3) pour simuler la distribution des valeurs.
Cet exercice n'est pas réaliste parce que dans le cas de cancer colorectal, tous les patients n'ont pas forcément de toxicité. Il faudrait donc répartir les 670 patients en un groupe de patients sans toxicité et en un autre groupe de patients avec toxicité puis répartir équiprobablement les grades de toxicité dans ce dernier groupe. D'autre part les toxicités sont en général associées à des probabilités de survenir, non fournies par l'énoncé.
Remarque : il est d'usage d'autoriser les effectifs théoriques à ne pas être entiers pour éviter les problèmes d'arrondi. Ainsi avec les 670 patients, on conserve un effectif théorique de 223,33.
Consulter notre page http://www.info.univ-angers.fr/~gh/vitrine/Democgi/loisStatp.htm qui donne les principales lois probabilistes discrètes. Un rappel de la notion de loi de probabilité est ici. Voici leurs noms et la base des fonctions correspondantes en R (lien sous le nom de la fonction) :
loi binomiale binom wiki français wiki anglais loi de Poisson pois wiki français wiki anglais loi uniforme discrète rep(1/n,n) wiki français wiki anglais loi binomiale négative nbinom wiki français wiki anglais loi géométrique geom wiki français wiki anglais loi hyper-géométrique hyper wiki français wiki anglais loi triangulaire discrète triang (dans le package mc2d) wiki français wiki anglais loi de Benford benf (dans le package VGAM) wiki français wiki anglais Pour les convergences, en deux mots : sous certaines conditions, Binomiale(n,p) converge vers Poisson(np) ou vers Normale(np, np(1-p)).
Il y a de nombreuses lois continues que nous présentons aussi dans le tableau ci-dessous. pour être complet, il faut aussi lister la loi de Rayleigh, la loi de Rice, la loi d'Erlang, la loi de Lévy, la loi gamma-inverse, la loi log-normale, la loi de Cauchy, la loi de Laplace, la loi de Pareto, la loi de Gumbel et enfin la loi « stable ».
loi normale norm wiki français wiki anglais loi uniforme continue unif wiki français wiki anglais loi beta beta wiki français wiki anglais loi gamma gamma wiki français wiki anglais loi exponentionellle exp wiki français wiki anglais loi du chi2 chisq wiki français wiki anglais loi F de Fisher f wiki français wiki anglais loi t de Student t wiki français wiki anglais loi de Weibull weibull wiki français wiki anglais La loi du chi2 est la somme de lois normales au carré, la loi de Fisher est le rapport de deux lois du chi2.
A propos des des lois et des convergences, on pourra consulter lois usuelles (PDF) et surtout lire l'ouvrage SPRAST dont nous reproduisons ci-dessous la page 161 :
On pourra aussi relire les exercices 10 et 11 de la séance précédente et leur solution.
Avec 50 naissances, l'hypothèse d'équiprobabilité autorise à utiliser la loi uniforme discrète à deux valeurs (car il y a deux sexes) cela nous fournit comme fréquences théoriques les valeurs 25 et 25. On doit donc réaliser un Chi-deux de conformité (ou Chi-deux d'adéquation) entre les effectifs observés et les effectifs théoriques attendus selon la formule :
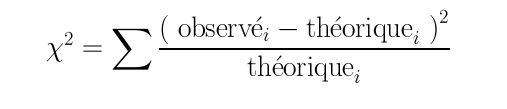
que l'on doit appliquer aux données suivantes :
Filles Garçons Effectifs observés 29 21 Effectifs théoriques 25 25 Le calcul du Chi-deux n'est donc qu'une somme pondérée (par les valeurs théoriques) des carrés des différences entre les valeurs théoriques et les valeurs observées. Chaque terme de la somme est nommé contribution au Chi-deux.
L'instruction R chisq.test( c(29,21), p=c(0.5,0.5) ) réalise le test demandé. Voici son résultat :
Chi-squared test for given probabilities data: c(21, 29) X-squared = 1.28, df = 1, p-value = 0.2579On en déduit qu'on ne peut pas refuser l'hypothèse nulle d'équirépartition des naissances entre garçons et filles (p=0,26).
Si on multiplie tout par 10, alors les résultats sont inversés. Et le "bricolage" de l'étudiant tombe à l'eau :
> chisq.test( c(210,290), p=c(0.5,0.5) ) Chi-squared test for given probabilities data: c(210, 290) X-squared = 12.8, df = 1, p-value = 0.0003466 > chisq.test( c(212,288), p=c(0.5,0.5) ) Chi-squared test for given probabilities data: c(212, 288) X-squared = 11.552, df = 1, p-value = 0.0006768En conclusion, on retiendra qu'un test sur des proportions utilise l'effectif total. Il ne suffit donc pas d'avoir les mêmes proportions pour avoir le même résultat du test. En d'autres termes, 30 % de personnes malades pour un effectif total de 100 personnes n'a pas forcément la même signification que 30 % de personnes malades pour un effectif total de 850 personnes.
Remarque : les conditions d'application du test du Chi-deux (nommé Chi-square test en anglais) sont vérifiées ici.
Pour chacun des n enfants dans une famille de n enfants, l'hypothèse la plus "raisonnable" est de supposer que la naissance d'un garçon et d'une fille sont équiprobables et indépendantes, ce qui est certainement "faux localement" et "vrai globalement" (car la physiologie de certaines femmes les favorise à avoir plutôt des enfants d'un sexe donné). Modélisant par X=0 la naissance d'un garçon et par X=1 la naissance d'une fille avec une loi de Bernoulli b(p), le nombre de filles dans une une famille de n enfants est donc la somme de n lois de Bernoulli supposées indépendantes et de même paramètre p qui est donc une loi binomiale B(n,p) avec p=0,5 comme valeur la plus probable.
Voici les instructions R pour calculer les fréquences théoriques et effectuer le calcul du Chi-deux correspondant :
# paramètres de la loi binomiale n <- 4 # 4 enfants par famille p <- 0.5 # hypothèse d'équiprobabilité H/F # fréquences théoriques fth <- dbinom( 0:n, n, p) # effectifs observés eobs <- c(18,55,21,12,4) # effectifs théoriques eth <- fth*sum( eobs ) # différences dif <- eobs-eth # carré des différences cdif <- dif*dif # carré pondéré des différences (=contribution) cpdif <- cdif/eth # cumul des carrés pondérés des différences scpd <- cumsum( cpdif) # test du Chi-deux testc <- chisq.test( eobs, p=fth) # restructuration et affichage des données data <- rbind( fth, eth, eobs,dif,cdif,cpdif,scpd ) row.names(data) <- c("Fréquences théoriques", "Effectifs théoriques", "Effectifs observés", "Différences", "Carrés des diff.", "Contributions", "Somme des ctr.") colnames(data) <- 0:n cat("Données\n") print(data) # résultats du test print( testc ) # le graphique en barres s'obtiendrait par # # barplot(rbind(eobs,eth),beside=TRUE) #Comme le montre les résultats suivants, on peut rejeter l'hypothèse nulle que les données suivent le modèle théorique (p<10-12).
Données 0 1 2 3 4 Fréquences théoriques 0.06250 0.25000 0.37500 0.250000 0.062500 Effectifs théoriques 6.87500 27.50000 41.25000 27.500000 6.875000 Effectifs observés 18.00000 55.00000 21.00000 12.000000 4.000000 Différences 11.12500 27.50000 -20.25000 -15.500000 -2.875000 Carrés des diff. 123.76562 756.25000 410.06250 240.250000 8.265625 Contributions 18.00227 27.50000 9.94091 8.736364 1.202273 Somme des ctr. 18.00227 45.50227 55.44318 64.179545 65.381818 Chi-squared test for given probabilities data: eobs X-squared = 65.3818, df = 4, p-value = 2.138e-13Si on veut avoir plus de détails sur les contributions et disposer de graphiques, sans avoir à tout écrire à la main, on peut utiliser notre fonction chi2Adeq comme suit :
> chi2Adeq(eth,eobs,TRUE,TRUE,"chi2_filles") CALCUL DU CHI-DEUX D'ADEQUATION Valeurs théoriques 6.875 27.5 41.25 27.5 6.875 Valeurs observées 18 55 21 12 4 Valeur du chi-deux 65.38182 Chi-deux max (table) à 5 % 9.487729 pour 4 degrés de liberté ; p-value 2.138116e-13 Décision : au seuil de 5 % on peut rejeter l'hypothèse que les données observées correspondent aux valeurs théoriques. Contributions au chi-deux Ind. The Obs Dif Cntr Pct Cumul 1 6.875 18 -11.125 18.002273 27.534066 18.00227 2 27.500 55 -27.500 27.500000 42.060623 45.50227 3 41.250 21 20.250 9.940909 15.204394 55.44318 4 27.500 12 15.500 8.736364 13.362069 64.17955 5 6.875 4 2.875 1.202273 1.838849 65.38182 Vous pouvez utiliser chi2_filles1.png et chi2_filles2.pngCela permet notamment de constater que la plus grande différence (contribution de 42 %) est imputable à la valeur "une seule fille dans la famille".
L'utilisation des sex-ratio européen (p=100/206) et chinois ((p=100/217) modifie peu la probabilité p (respectivement 0,5 ; 0,4854369 ; 0,4608295) et les conclusions sont les mêmes, avec toutefois des probabilités critiques (ou p-values en anglais) différentes (respectivement 2,138e-13 ; 3,488e-11 ; 3,776e-08). Voici en résumé les fréquences utilisées (arrondies)
Nombre de filles dans la famille 0 1 2 3 4 Valeurs observées 18 55 21 12 4 Valeurs théoriques (équiprobabilité) 7 28 41 28 7 Valeurs théoriques (sex-ratio européen) 8 29 41 26 6 Valeurs théorique (sex-ratio chinois) 9 32 41 23 5 Avec n=820 personnes, on a n/2=410 hommes et 410 femmes sous hypothèse d'équiprobabilité. Puisque 5 % des gens sont résistants à la tétracycline on a n*5/100=41 et personnes résistantes et n*95/100=779 personnes non résistantes. On peut donc partiellement construire le tableau de contingence suivant sous hypothèse d'indépendance :
Femme Homme total Résistant à la tétracycline 41 Non résistant 779 total 410 410 820 Compte-tenu de l'équirépartition des sexes, il suffit de diviser 41 par 2 et 779 par 2 pour compléter le tableau. Dans le cas général, la valeur théorique attendue dans une case s'obtient en multipliant le total de la ligne par le total de la colonne correspondante, le tout divisé par le total général. Ainsi 20,5 s'obtient par le calcul 41*410/820.
Femme Homme total Résistant à la tétracycline 20,5 20,5 41 Non résistant 389,5 389,5 779 total 410 410 820 On peut étudier les données QL du fichier tetracyclin.dar par
# lecture des données antibio <- lit.dar("http://forge.info.univ-angers.fr/~gh/wstat/Eda/tetracyclin.dar") sexe <- antibio[,1] resi <- antibio[,2] # "à la main" avec les fonctions R cat("Comptages élémentaires\n") print( table(sexe) ) print( table(resi) ) print( table(sexe,resi) ) # avec nos fonctions decritQL("SEXE dossier Antibio",sexe,"homme femme",TRUE,"tetracyclin_sexe.png") decritQL("RESISTANCE dossier Antibio",resi,"non oui",TRUE,"tetracyclin_resi.png") triCroise("SEXE dossier Antibio",sexe,"homme femme", "RESISTANCE dossier Antibio",resi,"non oui", TRUE,"tetracyclin_sxrs.png")Et on obtient alors
Comptages élémentaires sexe 1 2 412 408 resi 0 1 732 88 resi sexe 0 1 1 381 31 2 351 57 QUESTION : SEXE dossier Antibio (ordre des modalités) homme femme Total Effectif 412 408 820 Frequence (en %) 50 50 100 Cumul fréquences 50 100 100 QUESTION : SEXE dossier Antibio (par fréquence décroissante) homme femme Total Effectif 412 408 820 Frequence (en %) 50 50 100 Cumul fréquences 50 100 100 QUESTION : RESISTANCE dossier Antibio (ordre des modalités) non oui Total Effectif 732 88 820 Frequence (en %) 89 11 100 Cumul fréquences 89 100 100 QUESTION : RESISTANCE dossier Antibio (par fréquence décroissante) non oui Total Effectif 732 88 820 Frequence (en %) 89 11 100 Cumul fréquences 89 100 100 TRI CROISE DES QUESTIONS : SEXE dossier Antibio (en ligne) RESISTANCE dossier Antibio (en colonne) Effectifs non oui homme 381 31 femme 351 57 Valeurs en % du total non oui TOTAL homme 46 4 50 femme 43 7 50 TOTAL 89 11 100 CALCUL DU CHI-DEUX D'INDEPENDANCE ================================= TABLEAU DES DONNEES homme femme Total non 381 351 732 oui 31 57 88 Total 412 408 820 VALEURS ATTENDUES et MARGES homme femme Total non 368 364 732 oui 44 44 88 Total 412 408 820 CONTRIBUTIONS SIGNEES homme femme non + 0.475 - 0.479 oui - 3.950 + 3.988 Valeur du chi-deux 8.892026 Le chi-deux max (table) à 5 % est 3.841459 ; p-value 0.004116124 pour 1 degrés de liberte décision : au seuil de 5 % on peut rejeter l'hypothèse qu'il y a indépendance entre ces deux variables qualitatives. PLUS FORTES CONTRIBUTIONS AVEC SIGNE DE DIFFERENCE Signe Valeur Pct Mligne Mcolonne Obs Th + 3.988 44.85 % oui femme 57 43.8 - 3.950 44.42 % oui homme 31 44.2 - 0.479 5.39 % non femme 351 364.2 + 0.475 5.34 % non homme 381 367.8
L'étude séparée des QL montre que la répartition Femme/Homme est à peu près équilibrée (de façon plus précise, il y a 50,2 % d'hommes et 49,8 % de femmes) alors que la disproportion de résistance à l'antibiotique ne semble pas correspondre aux pourcentages attendus (10,7 % de résistants au lieu des 5 % indiqués par le magazine).
Le tri croisé montre une proportion de femmes résistantes (57 sur 408 soit presque 14 %) très supérieure à celles des hommes (31 sur 412 soit 7,5 %). Le calcul du Chi-deux rejette l'hypothèse nulle d'indépendance entre les deux variables qualitatives : il y a en effet trop de femmes résistantes observées (57) au lieu des 43,8 attendues, soit une contribution de 44,85 % au Chi-deux. De même, il n'y a pas assez d'hommes résistants (31 au lieu de 44,2, soit une contribution de 44,42 %). On peut donc dire que le sexe et la résistance sont dépendants. La phrase "le sexe influe sur la résistance" est possible, alors que la phrase "la résistance influe sur le sexe" n'a aucun sens. On se méfiera donc du fait que le test est symétrique au niveau des variables alors que souvent on "veut" un sens de causalité c'est-à-dire une relation dissymétrique.
Il n'y a pas vraiment de différence entre les deux termes. Certains auteurs réservent le terme de chi-deux d'indépendance pour deux variables sur un même échantillon et celui de Chi-deux d'homogénéité pour une même variable sur deux échantillons mais ce n'est pas un usage général. Il vaut sans doute mieux considérer les termes comme équivalents.
Voici les résultats du test avec chisq.test puis le détail des calculs avec notre fonction chi2IndepTable.
# introduction des valeurs tap <- 33 # traitement avec polio tsp <- 200712 # traitement sans polio pap <- 115 # placebo avec polio psp <- 201114 # placebo sans polio # restructuration en matrice meier <- rbind( c(tap,tsp), c(pap,psp) ) row.names(meier) <- c("traitement","placebo") colnames(meier) <- c("avec_polio","sans_polio") # affichage pour vérificaton print(meier) # calcul du chi-deux print( chisq.test(meier) ) # détail du calcul avec nos fonctions chi2IndepTable(meier,row.names(meier),colnames(meier))Données : avec_polio sans_polio traitement 33 200712 placebo 115 201114 Pearson's Chi-squared test with Yates' continuity correction data: meier X-squared = 44.1526, df = 1, p-value = 3.038e-11 CALCUL DU CHI-DEUX D'INDEPENDANCE ================================= TABLEAU DES DONNEES avec_polio sans_polio Total traitement 33 200712 200745 placebo 115 201114 201229 Total 148 401826 401974 VALEURS ATTENDUES et MARGES avec_polio sans_polio Total traitement 74 2e+05 2e+05 placebo 74 2e+05 2e+05 Total 148 4e+05 4e+05 CONTRIBUTIONS SIGNEES avec_polio sans_polio traitement - 22.645 + 0.008 placebo + 22.590 - 0.008 Valeur du chi-deux 45.25191 Le chi-deux max (table) à 5 % est 3.841459 ; p-value 3.037545e-11 pour 1 degrés de liberte décision : au seuil de 5 % on peut rejeter l'hypothèse qu'il y a indépendance entre ces deux variables qualitatives. PLUS FORTES CONTRIBUTIONS AVEC SIGNE DE DIFFERENCE Signe Valeur Pct Mligne Mcolonne Ligne Colonne Obs Th - 22.645 50.04 % traitement avec_polio 1 1 33 73.9 + 22.590 49.92 % placebo avec_polio 2 1 115 74.1 + 0.008 0.02 % traitement sans_polio 1 2 200712 200671.1 - 0.008 0.02 % placebo sans_polio 2 2 201114 201154.9On peut donc en conclure qu'avoir la poliomélite et recevoir le vaccin sont dépendants (p=3e-11). Les contributions montrent qu'on observe moins de cas de poliomélite (33 vs 74) avec le vaccin que sous hypothèse d'indépendance et plus de cas de poliomélite (115 vs 74) sans le vaccin que sous hypothèse d'indépendance. On notera toutefois que dans les deux cas, l'incidence de la maladie reste très faible : 33/(200712+33 soit 0.0164 % pour le vaccin et 115/(115+201114) soit 0.0571 pour le groupe placebo.
A priori, non, encore faut-il le vérifier. Maintenant la "vraie" question est plutôt «Y a-t-il une différence significative entre ces nombres ?». Il faut bien sûr commencer par rapatrier la séquence du gène. Le plus simple est sans doute d'utiliser la fonction read.GenBank du package ape (avec un jeu de mots sur l'acronyme du package qui est mis pour Analyses of Phylogenetics and Evolution) :
# chargement de la librairie library(ape) # lecture du gène demandé geneX <- read.GenBank("X94991.1",as.character=TRUE) # comptage par type de nucléotide table(geneX) # un chi-deux rapide print(chisq.test(table(geneX))) # un chi-deux détaillé en français avec conclusion chi2Adeq(rep(length(geneX[[1]])/4,4),table(geneX)) # au passage, comment était stockée la séquence du gène ? print( ls.str(geneX) )geneX a c g t 410 789 573 394 Chi-squared test for given probabilities data: table(geneX) X-squared = 187.0674, df = 3, p-value < 2.2e-16 CALCUL DU CHI-DEUX D'ADEQUATION Valeurs théoriques 541.5 541.5 541.5 541.5 Valeurs observées 410 789 573 394 Valeur du chi-deux 187.0674 Chi-deux max (table) à 5 % 7.814728 pour 3 degrés de liberté ; p-value 2.62465e-40 décision : au seuil de 5 % on peut rejeter l'hypothèse que les données observées correspondent aux valeurs théoriques. X94991.1 : chr [1:2166] "c" "g" "g" "c" "c" "c" "g" "g" "c" "c" "a" "t" "g" "g" "c" "g" "g" "c" "c" "c" "c" "c" "c" "g" "c" "c" "c" "g" ...Remarque : X94991 est décrit au NCBI par GI:1155087 et semble donc être relié à la zyxine.
Il pourrait être intéressant de regarder un peu plus en détail les données et les pourcentages de nucléotides. Voici un script qui permet de le faire :
############################################# # # # comptage des nucléotides du gène X94991 # # puis pourcentages et graphiques # # # ############################################# # chargement de la librairie library(ape) # lecture du gène demandé geneX <- read.GenBank("X94991.1",as.character=TRUE) # tri à plat des nucléotides du gène tap <- table(geneX) # répartition détaillée des nucléotides props <- as.numeric(prop.table(tap)) pcts <- paste(round(100*props,1),"%") dfRes <- data.frame(tap,props,pcts) names(dfRes) <- c("Nucléotides","Comptages","Proportions","Pourcentages") print(dfRes) # visualisation graphique lng <- sum(tap) coul <- rainbow(dim(tap)) # mieux que c("red","green","blue","yellow") titre <- paste("Nucléotides du gène X94991\n (longueur=",lng,")",sep="") barplot(tap,main=titre,col=coul,legend.text=pcts,xlim=c(0,6))Nucléotides Comptages Proportions Pourcentages 1 a 410 0.1892890 18.9 % 2 c 789 0.3642659 36.4 % 3 g 573 0.2645429 26.5 % 4 t 394 0.1819021 18.2 %Le tri se fait par sort et les indices de classement avec order ; on obtient les rangs avec rank. Il y a des options pour les ex-aequo avec rank. En voici une démonstration :
> # tri croissant de ech1 > sort(ech1) 125 130 132 135 136 138 140 145 > # tri décroissant de ech1, solution 1 > rev( sort(ech1) ) 145 140 138 136 135 132 130 125 > # tri décroissant de ech1, solution 2 > sort(ech1,decreasing=TRUE) 145 140 138 136 135 132 130 125 > # indexation de ech1 > order(ech1) 8 2 7 4 5 6 3 1 > # vérification 1 > ech1[ order(ech1) ] 125 130 132 135 136 138 140 145 > # vérification 2 > ech1[ order(ech1) ] == sort(ech1) TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE > # tri des colonnes ech1 et ech2 appariées > # selon l'ordre croissant sur ech1 > > ind <- order(ech1) > ech1_tri <- ech1[ ind ] > ech2_tri <- ech2[ ind ] > # calcul des rangs sans ex-aequo > rank(ech1) 8 2 7 4 5 6 3 1 > # calcul des rangs avec ex-aequo (par défaut) > rank(jour1) 1.0 2.0 3.5 3.5 5.0 6.0 7.0 8.0 > # calcul des rangs avec ex-aequo suivant > # ties.method = c("average", "first", "random", "max", "min") > rank(jour1,ties.method = "average") 1.0 2.0 3.5 3.5 5.0 6.0 7.0 8.0 > rank(jour1,ties.method = "first") 1 2 3 4 5 6 7 8 > rank(jour1,ties.method = "random") 1 2 3 4 5 6 7 8 > rank(jour1,ties.method = "max") 1 2 4 4 5 6 7 8 > rank(jour1,ties.method = "min") 1 2 3 3 5 6 7 8Voici les calculs,
# lecture des données series <- lit.dar("http://forge.info.univ-angers.fr/~gh/wstat/Eda/cognitif.dar") # ou # # series <- lit.dar("cognitif.dar") # # serveur <- c("http://forge.info.univ-angers.fr/") # adresse <- c("~gh/wstat/Eda/cognitif.dar") # url <- paste(serveur,adresse,sep="") # series <- lit.dar( url ) # # si vous n'avez pas recopié le fichier des données # sur votre disque dur # attach(series) iden <- row.names(series) ser1 <- Série_1 ser2 <- Série_2 # description séparée des données decritQT("Série 1",ser1,"points",TRUE,"ser1.png") decritQT("Série 2",ser2,"points",TRUE,"ser2.png") # si on veut voir les graphiques au lieu d'en faire des images .png # écrire seulement : # # decritQT("Série 1",ser1,"points",TRUE) # decritQT("Série 2",ser2,"points",TRUE) # description conjointe et comparaison compMoyData("Deux séries de questions","Série 1",ser1,"Série 2",ser2) compare2QT("Deux séries de questions","1",ser1,"2",ser2,"points",TRUE) # calculs diff <- ser1 - ser2 idnn <- diff!=0 vidn <- iden[ idnn ] vse1 <- ser1[ idnn ] vse2 <- ser2[ idnn ] vdif <- vse1 - vse2 adif <- abs(vdif) rdif <- rank(adif,ties.method="average") sdif <- sign(vdif)*rdif valw <- sum(sdif) nbp <- length(vdif) # affichages cat(" pour n = ",nbp," scores différents, la différence moyenne est ") ; cat(mean(diff)," et W vaut ",valw,"\n\n") ; cat(" Détail des calculs : \n") mres <- cbind(vse1,vse2,vdif,adif,rdif,sdif) row.names(mres) <- vidn print( mres ) detach(series)les résultats et les graphiques :
VARIABLE Série 1 VARIABLE Série 2 Taille 16 individus Taille 16 individus Moyenne 56.6875 points Moyenne 48.9375 points Ecart-type 20.4167 points Ecart-type 17.4623 points Coef. de variation 36 % Coef. de variation 36 % 1er Quartile 43.75 points 1er Quartile 35 points Mediane 58 points Mediane 52 points 3eme Quartile 73.5 points 3eme Quartile 63.5 points iqr 29.75 points iqr 28.5 points Minimum 22 points Minimum 20 points Maximum 90 points Maximum 78 points Tracé tige et feuilles Tracé tige et feuilles The decimal point is 1 digit(s) The decimal point is 1 digit(s) to the right of the | to the right of the | 2 | 240 2 | 04526 4 | 05002 4 | 048668 6 | 444288 6 | 28888 8 | 40 COMPARAISON DE MOYENNES (valeurs fournies) : Deux séries de questions Variable NbVal Moyenne Variance Ecart-type Cdv Série 1 16 56.688 444.629 21.086 37 % Série 2 16 48.938 325.262 18.035 37 % Global 32 52.812 388.028 19.698 37 % différence réduite : 1.1172 ; p-value 0.2729705 au seuil de 5 % soit 1.96, on ne peut pas rejeter l'hypothèse d'égalité des moyennes. En d'autres termes, il n'y a pas de différence significative entre les moyennes au seuil de 5 %. Shapiro-Wilk normality test data: varQt1 W = 0.9589, p-value = 0.6421 Shapiro-Wilk normality test data: varQt2 W = 0.9494, p-value = 0.4805 F test to compare two variances data: varQt1 and varQt2 F = 1.367, num df = 15, denom df = 15, p-value = 0.5524 alternative hypothesis: true ratio of variances is not equal to 1 95 percent confidence interval: 0.4776176 3.9124394 sample estimates: ratio of variances 1.366986 Welch Two Sample t-test data: varQt1 and varQt2 t = 1.1172, df = 29.296, p-value = 0.2730 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -6.430988 21.930988 sample estimates: mean of x mean of y 56.6875 48.9375 Wilcoxon rank sum test with continuity correction data: varQt1 and varQt2 W = 156, p-value = 0.2993 alternative hypothesis: true location shift is not equal to 0 VARIABLE QT Deux séries de questions unité : points VARIABLE QL Groupes labels : 1 2 N Moy Unite Ect Cdv Q1 Med Q3 EIQ Min Max Global 32 52.8125 points 19.3882 37 39 54 68 29 20 90 1 16 56.6875 points 20.4167 36 43.75 58 73.5 29.75 22 90 2 16 48.9375 points 17.4623 36 35 52 63.5 28.5 20 78 Analysis of Variance Table Response: nomVarQT Df Sum Sq Mean Sq F value Pr(>F) as.factor(nomVarQL) 1 480.5 480.5 1.2482 0.2728 Residuals 30 11548.4 384.9 Pour n = 14 scores différents, la différence moyenne est 7.75 et W vaut 67 Détail des calculs : vse1 vse2 vdif adif rdif sdif P03 64 62 2 2 1.0 1.0 P04 45 48 -3 3 2.0 -2.0 P05 64 68 -4 4 3.5 -3.5 P06 52 56 -4 4 3.5 -3.5 P07 30 25 5 5 5.0 5.0 P08 50 44 6 6 6.0 6.0 P09 64 56 8 8 7.0 7.0 P10 50 40 10 10 8.5 8.5 P11 78 68 10 10 8.5 8.5 P12 22 36 -14 14 10.0 -10.0 P13 84 68 16 16 11.0 11.0 P14 40 20 20 20 12.0 12.0 P15 90 58 32 32 13.0 13.0 P16 72 32 40 40 14.0 14.0La statistique de test est nommée somme des rangs signés et s'apparente à un test de Wilcoxon. Voir la page Wilcoxon Signed-Rank Test qui utilise les mêmes données. L'ensemble du cours, bien rédigé, est à l'adresse : Concepts and Applications of Inferential Statistics.
On peut en conclure que les deux séries d'exercices n'ont pas de différence significative. Le test non paramétrique de Kruskal-Wallis fournit les mêmes résultats :
> wilcox.test(ser1,ser2) Wilcoxon rank sum test with continuity correction data: ser1 and ser2 W = 156, p-value = 0.2993 alternative hypothesis: true location shift is not equal to 0 > kruskal.test(list(ser1,ser2)) Kruskal-Wallis rank sum test data: list(ser1, ser2) Kruskal-Wallis chi-squared = 1.1169, df = 1, p-value = 0.2906- Voir notre page bismtd2 pour le rappel des tests usuels non paramétriques en regard des tests paramétriques. On pourra aussi cliquer sur les liens ci-dessous pour voir la page d'aide pour l'utilisation en R du test correspondant.
Leur utilisation est semblable à celles des test paramétriques. Ainsi wilcox.test(x,y) se substitue à t.test(x,y) et friedman.test(y ~ x) est semblable à anova(lm(y ~ x)).
test de Mann-Whitney wiki correspondant test de Wilcox wiki correspondant test de Kruskal-Wallis wiki correspondant test de Friedman wiki correspondant Les résultats obtenus, à savoir :
> cor( SERIE1, SERIE2, method="pearson") 0.7593638 > cor( rank(SERIE1), rank(SERIE2)) 0.7724242 > cor( rank(SERIE1), rank(SERIE2), method="pearson") 0.7724242 > cor( SERIE1, SERIE2, method="spearman") 0.7724242montrent que le calcul de la corrélation sur des QT avec la méthode de Spearman est identique à la corrélation traditionnelle (Pearson) sur les rangs de ces mêmes QT. C'est pourquoi on la nomme corrélation des rangs de Spearman. Il y a un test correspondant, nommé cor.test qui peut s'utiliser en R avec les trois méthodes possibles (pearson, kendall et spearman).
Dans le cadre de tests diagnostiques, on s'intéresse à l'efficacité du test, c'est-à-dire on cherche à savoir s'il détecte bien la maladie chez les gens malades ("vrais positifs") et s'il garantit bien que des gens non malades sont diagnostiqués comme tels ("vrais négatifs").
A partir des 4 effectifs correspondant aux croisement des QL maladie (modalités malades et non malades) et diagnostic (modalités test positif / négatif), on construit de nombreux indicateurs, dont la spécificité (probabilité que le test soit négatif pour un non malade) et la sensibilité (probabilité que le test soit positif pour un malade). Lorsqu'un test est calculé par régression logistique (ce qui fournit un "score" entre 0 et 1), on peut calculer les courbes des valeurs diagnostiques en fonction du score pour des individus dont on sait s'ils sont malades ou non. La courbe ROC correspond au tracé de y=sensibilité en fonction de x=(1-spécificité).
Vous trouverez sur notre page valeurs diagnostiques des exemples classiques et un formulaire pour calculer ces indicateurs. Les formules et le vocabulaire sont détaillés sur la page des résultats. En anglais, on pourra lire la page receiver operating characteristic curve qui présente aussi comment on trace une courbe ROC. Notre formulaire ROC en ligne permet de comprendre ces notions par l'exemple (courbe de Youden et autres indices de fiabilité compris).
La plupart des calculs pour les valeurs diagnostiques sont arithmétiques et donc simples à effectuer. Par contre les tests utilisés, comme le test de Mc Nemar ou le test de Cohen requièrent des packages comme irr (interrater reliability and agreement).
Pour les courbes ROC, de nombreux packages sont disponibles, dont pROC, ROCR.
Retour à la page principale de (gH)