Exemple naif de régression logistique
pour une entrée quantitative
et une sortie qualitative binaire
Présentation des données
On dispose d'un fichier de données nommé pg.dar contenant un identifiant, la valeur de taille exprimée en centimètres et le groupe des individus "connus". On voudrait en déduire le groupe des individus "inconnus" du fichier pginc.dar. Cet exemple est simple parce qu'on va essayer de prédire la valeur du GROUPE à partir d'une seule variable, la TAILLE.
Fichier PG.DAR
Fichier PGINC.DAR
Détails des calculs
Le tracé du groupe en fonction de la taille
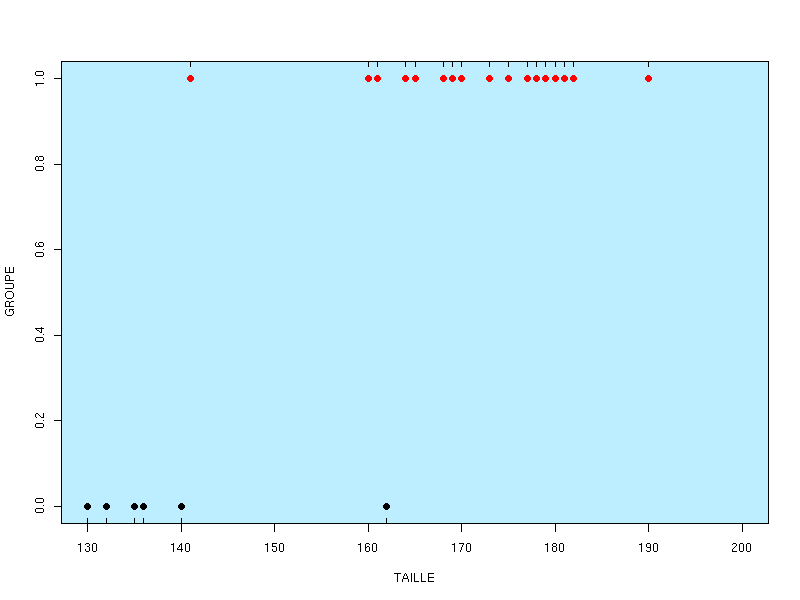
montre que les groupes sont assez bien séparés, ce qui arrive rarement. C'est pourquoi il s'agit d'un exemple naif, non réel mais facile à suivre. L'utilisation de la procédure LOGISTIC du logiciel SAS via le fichier-programme reglogi_sas.txt fournit de nombreux résultats (fichiers reglogi_lst.txt et reglogi_log.txt) dont les coefficients de régression logistique
a = 0,1812 et b = -27.2103.
Nous allons retrouver et exploiter ces valeurs à l'aide du logiciel de R soit le fichier-programme reglogi_r.txt. A l'aide de la fonction logit et des formules
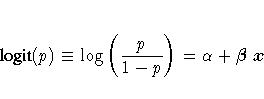
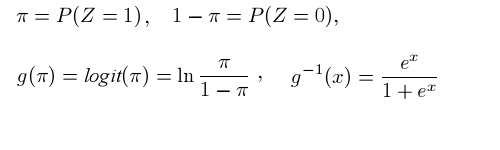
nous construisons un prédicteur qui associe à une taille un nombre réel entre 0 et 1. Il suffit de situer ce nombre sur la courbe de régression pour en déduire le groupe, soit ici en prenant la partie entière de nos valeurs.
On peut donc prédire comme groupe pour nos "inconnus" les valeurs
TAILLE GROUPE B01G 164 1 B02G 200 1 B03P 147 0La valeur du rapport de cotes ("odds ratio") s'obtient alors avec l'exponentielle de la pente de la courbe soit ici exp(0,1812) donc à peu près 1,198655.
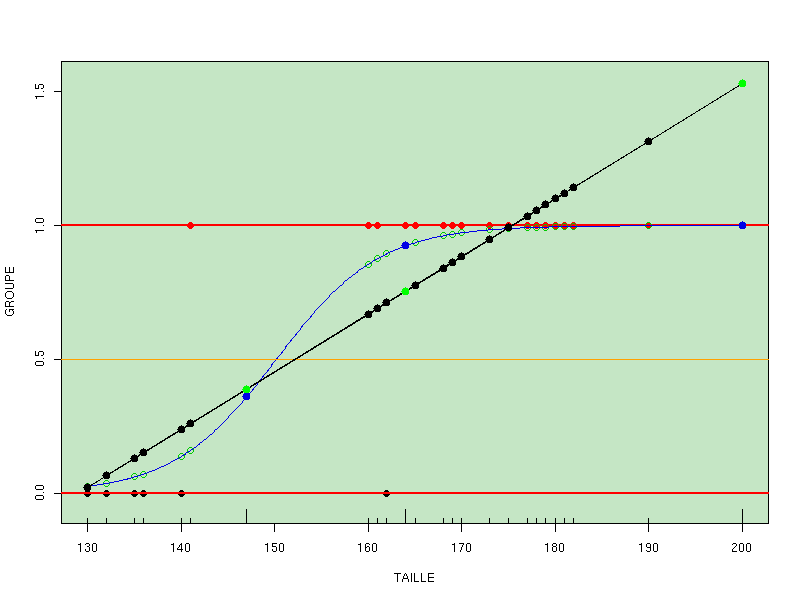
L'illustration de la méthode et des résultats est fournie par le graphique suivant où les points bleus correspondant aux individus "inconnus" :
On aurait pu se demander si une régression linéaire classique n'aurait pas suffi. La réponse est non, bien sûr, fournie par le graphique suivant : 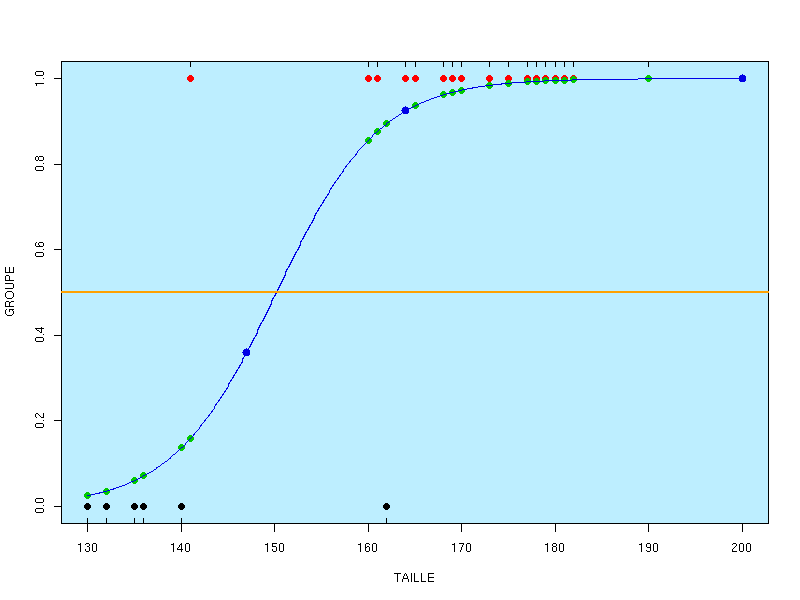
Pour aller plus loin
Un cours détaillé (PDF, 60 pages) uniquement sur la régression logistique est celui de Patrick Taffé (en français). Vous pouvez aussi consulter cet exemple commenté pour SAS (en anglais) et cette présentation des résultats de SAS également en anglais pour les réponses dichotomiques et polytomiques sans oublier le cours général de modélisation statistique du Pr. BESSE (PDF, 80 pages).
Pour une interprétation de ces calculs en médicine, on pourra consulter
- le site SMEL (Statistique Médicale En Ligne) notamment pour la définition du rapport de cotes, de la sensibilité et de la spécificité,
- les pages du cours de Méthodologie et interprétation des essais thérapeutiques de Lyon et en particuier le chapitre sur les indices d'efficacité qui détaillent le rapport de cotes et le risque relatif,
- quelques réflexions sur les meta-analyses dans le cadre du cours de Lecture critique des essais cliniques dispensé dans formation diplomante d' interprétation des essais cliniques,
- une discussion nommée "à bas les odds-ratios" dans le journal EBM (Evidence-Based Medicine) en trois parties : juin 96 puis avril 97 et enfin mai 99,
- le texte sur la courbe Roc et la prévalence, les Faux Positifs et Faux Négatifs dans le chapitre 5 Evaluation de l'intérêt diagnostique des informations médicales du cours de Biostatistiques au CHUPS (Pitié-Salpêtrière),
- une autre présentation de la courbe ROC, du paramètre p, de la taille des essais cliniques et le risque de faux positifs dans le cours de Biostatistique Clinique, Epidémiologie et essais cliniques à Necker.
Une petite difficulté pour un problème simple
Lorsque la situation est flagrante, c'est à dire si les groupes sont séparables linéairement, comme par exemple pour les données rlf.dar
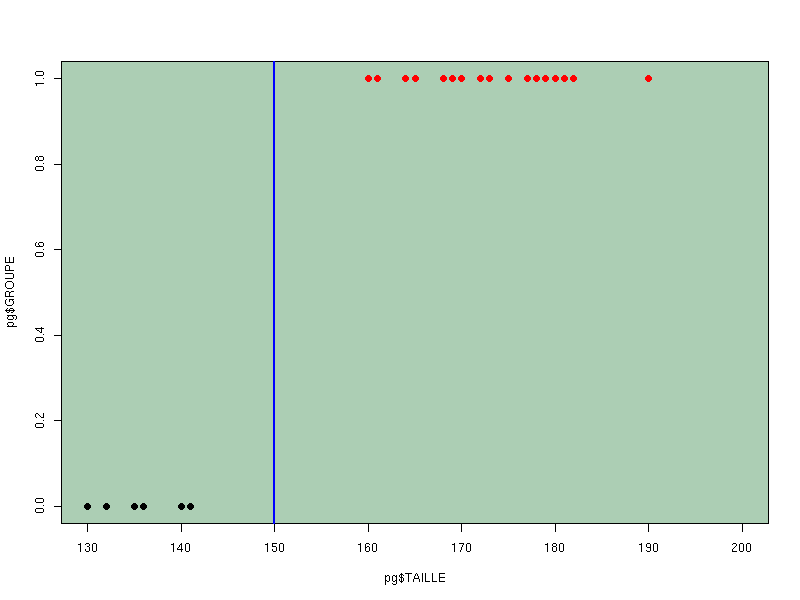
alors la plupart des méthodes théoriques ne sont pas capables de résoudre correctement le problème, même si la courbe de régression logistique est "magnifique" :
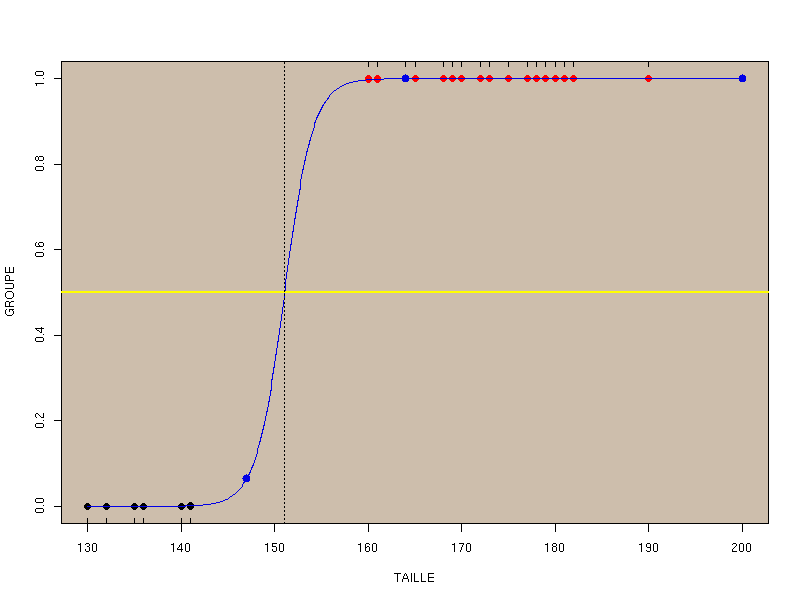
On pourra lire les programmes et les fichiers résultats correspondants pour s'en rendre compte :
 Retour à la page principale de
(gH)
Retour à la page principale de
(gH)