|
Solutions pour la séance numéro 2 (énoncés)
|
 Retour à la page principale de
(gH)
Retour à la page principale de
(gH)
Module de Biostatistiques,
partie 1
Ecole Doctorale Biologie Santé
gilles.hunault "at" univ-angers.fr
Solutions pour la séance numéro 2 (énoncés)
Dans le tableau 1 de l'article de Ratziu (2006), les résumés pour les QT sont nommés mean et se et présentés sous la forme mean (se). Mean est la moyenne et se l'erreur type (ou erreur standard). Voir le wiki anglais à ce sujet. Remarque : ce n'est jamais que l'écart-type de l'estimateur de la moyenne. On obtient se en divisant sd par la racine carrée de n, où n est la taille de l'échantillon. Pour plus de détails, consulter sd vs se (1), sd vs se (2) ou sd vs se (3).
Il n'est pas évident de choisir entre médiane et moyenne. L'usage veut qu'on utilise plutôt la moyenne quand les données ne sont pas "trop loin" d'une répartition normale et qu'il n'y a pas trop de valeurs extrêmes ; par exemple avec 1 3 5 7 on utilisera la moyenne alors qu'avec 1 3 5 70 on préférera la médiane. Ainsi dans l'article de Brocchieri (2005), la médiane est toujours utilisée car on a "régulièrement" des très grandes longueurs de protéines. Le choix entre sd et se est souvent plus simple : en médecine on utilise volontiers se pour décrire l'échantillon et sd pour décrire la population.
Remarque : s'il y a beaucoup de valeurs «extrêmes» (sans que ce soit des outliers), on peut calculer une moyenne tronquée (trimmed mean en anglais).
Le graphique de la figure 2 dans l'article de Ratziu est une boite à moustaches avec encoche (notched boxplot). Avant 2016 , Excel ne savait pas tracer les boxplots, avec ou sans encoche. Avec le logiciel R, il faut ajouter l'option notch=TRUE pour que les encoches soient tracées. Les encoches permettent la comparaison visuelle des médianes au sens du test de Mc Gill (McGill, R., Tukey, J. W., and Larsen, W. A. (1978), "Variations of Boxplots," The American Statistician, 32, 12-16.). Voir par exemple la figure boxnotch que l'on comparera à la figure boxplot pour comprendre comment sont tracés les boxplots classiques ou avec des encoches (copies locales ici et là).
Voici comment tracer des boxplots en R :
## deux exemples de boites à moustaches en R # utilisation des données iris data(iris) # tracé en jaune sans encoche de Sepal.Length # en fonction de l'espèce boxplot(Sepal.Length ~ Species,data=iris,col="yellow",main="Longueur sépale") # tracé en bleu clair avec encoche de Sepal.Width # en fonction de l'espèce # on utilise une syntaxe "agréable" à lire boxplot( Sepal.Width ~ Species, data=iris, col="lightblue", main="Largeur sépale", notch=TRUE, cex.main=3 ) # fin de boxplotLa documentation pour la fonction boxplot de R peut être lue ici et on trouvera sur notre page df quelques exemples comparés de boxplot et de beanplots.
Pour mémoire, rappelons que si help(boxplot) affiche l'aide de R sur la fonction boxplot, l'instruction example(boxplot) exécute des commandes montrant les possibilités offertes par cette fonction.
Pour une initiation aux statistiques via R , l'ouvrage collectif de PA. Cornillon, A. Guyader et al. nommé Statistiques avec R est suffisant. Pour un ouvrage plus conséquent, on pourra consulter The R book de M. Crawley (950 pages) même s'il date un peu (2007).
On trouvera dans notre Introduction à R une initiation aux divers graphiques de R en séance 3.
Pour les articles des doctorants, consulter analyses2019.txt que l'on pourra comparer aux analyses des années précédentes dans le fichier analyses.txt.
Pour des livres sur R, consulter la solution 14 de notre cours de Programmation avancée en R, tout en sachant que la majorité des ouvrages sont en anglais, comme on peut le voir à l'énoncé 14 de ce même cours.
Pour celles et ceux qui préférent lire des PDF gratuits, la Contributed Documentation du CRAN contient des ouvrages dans de nombreuses langues dont le français, sachant que la recherche google sur "cran software" filetype:pdf fournit aussi de nombreux PDF en ligne.
Pour la bioinformatique, la protéomique, la métabolomique, etc. voir introR, cours1, exercice 7.
La fonction R qui permet de lire des données-texte est read.table. Le détail des options est ici. En principe, un fichier "propre" contient en ligne 1 le nom des colonnes et en colonne 1 le nom des lignes. Les options header= et row.names= permettent de spécifier si c'est le cas. Entre autres options, na.strings= et skip= permettent de préciser les valeurs manquantes et le nombre de lignes à sauter avant de lire les données.
Pour lire un fichier Excel (de type .xls), il faut utiliser la fonction read.xls qui est dans le package nommé gdata. La liste complète et très impressionnante des packages est là. Comme il faut charger le package avant d'utiliser la fonction, pour lire le fichier elf.xls il faut donc écrire :
# chargement de la bibliothèque library(gdata) # lecture des données mesDonnees <- read.xls("elf.xls") # taille des données cat("Dimension : ",dim(mesDonnees),"\n")Remarques : si le package n'est pas installé, la commande install.packages("gdata") doit être exécutée. Il faut alors choisir un site pour le téléchargement, sauf si on utilise Rstudio qui s'occupe de tout.
Un fichier .csv est juste un fichier-texte dont le séparateur est la virgule et donc read.table suffit. Pour un fichier DBASE (dont le type est .dbf) qui garantit l'homogénéité d'une colonne, il faut utiliser la fonction read.dbf du package foreign. Enfin, pour des données de puces à ADN de type .gpr, la fonction read.Genepix du package marray faisait l'affaire mais ce package n'est plus disponible.
Avec statgh.r, on peut lire des données via la fonction lit.dar qui est un raccourci pour read.table avec les "bonnes" options.
Pratiquement toutes les fonctions de lecture renvoient un dataframe c'est-à-dire un tableau avec des lignes et des colonnes. Les fonctions dim(), names() et row.names() permettent alors de connaitre respectivement le nombre de lignes et de colonnes, le nom des colonnes et des lignes. L'instruction attach() rend les colonnes accessibles par leur nom. On accède à un élément via les indices df[i,j] (i pour la ligne i, j pour la colonne j). On peut aussi utiliser le nom des colonnes après la virgule, comme dans df[i,"AGE"]. Enfin, comme un dataframe est une liste on peut aussi utiliser la notation dollar comme dans df$AGE[i]. La notation [i,] désigne la ligne i et [,j] désigne la colonne j. On peut sélectionner des lignes et des colonnes avec des intervalles d'indices comme [(1:10),] qui désigne les dix premières lignes. Une sélection peut aussi se faire via des conditions logiques, comme AGE[SEXE==1]. On peut aussi utiliser la fonction which comme dans which(AGE>60) afin de connaitre les indices correspondants. Des indices négatifs correspondent à une exclusion et non pas à une sélection.
Attention : par défaut, R considére les données numériques comme des variables quantitatives. Si on a une colonne de codes, il est prudent d'utiliser as.factor et levels pour en faire une variable qualitative. Voici un exemple :
# apres read.table(...) la variable sexe est numérique # elle contient des 0 et des 1. # conversion en variable qualitative sexeQL <- as.factor(sexe) # définition du codage levels(sexeQL) <- c("homme","femme")Pour trier une seule série de valeurs, sort() suffit ; par contre pour trier simultanément plusieurs colonnes, il faut utiliser la fonction order().
On trouvera à l'adresse duclert un regroupement des fonctions de base de R par thème dans l'Aide-mémoire. Ce site contient aussi un menu pour les graphiques et un menu pour les statistiques.
Pour apprendre à programmer en R, l'utilisation de la page statghfns.php qui détaille statgh.r peut se révéler intéressante. Enfin, notre pot-pourri d'expressions R fournit quelques pratiques R pas toujours connues.
D'autres exemples de lecture de fichiers et de données structurées sont disponibles dans notre Introduction à R en séance 1 et séance 2.
Pour l'application qui consiste à ajouter les moyennes en haut de dataframe, voici une solution avec commentaires et le résultat de son exécution. Le détail des instructions sera vu en cours.
# lecture des données data(iris) # on retire la colonne 5 (ou on garde les 4 première colonnes) iris4 <- iris[, -5 ] # ou iris4 <- iris[,(1:4)] # calcul des moyennes en colonne moyIris <- apply(FUN=mean,X=iris4,MARGIN=2) # 1=lignes, 2=colonnes # nommage de ces moyennes names(moyIris) <- names(iris4) # ajout des moyennes en haut du data frame irism <- rbind(moyIris,iris4) row.names(irism)[1] <- "moyenne" # affichage du début des données print(head(irism))Sepal.Length Sepal.Width Petal.Length Petal.Width moyenne 5.843333 3.057333 3.758 1.199333 2 5.100000 3.500000 1.400 0.200000 3 4.900000 3.000000 1.400 0.200000 4 4.700000 3.200000 1.300 0.200000 5 4.600000 3.100000 1.500 0.200000 6 5.000000 3.600000 1.400 0.200000La moyenne et l'écart-type de l'échantillon qu'on nomme statistiques de l'échantillon permettent d'estimer la moyenne et l'écart-type de la population sous-jacente (nommés paramètres de la population et dénotés par des lettres grecques) : on prend pour la moyenne de la population la moyenne de l'échantillon car cela n'induit pas de biais. Par contre pour estimer l'écart-type de l'échantillon de la population, on multiplie l'écart-type de l'échantillon par la racine carrée du rapport n/n-1 où n est la taille de l'échantillon, ce qui donne les formules suivantes :
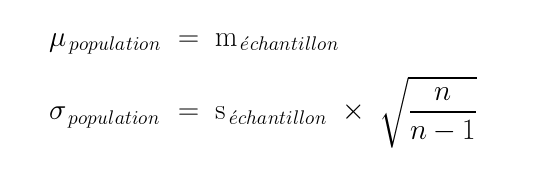
On nomme ponctuelles ces estimations car elles ne fournissent qu'une seule valeur (un seul point) contrairement aux intervalles de confiance qui donnent toute une plage de valeurs «sûres».
On écrit en général un intervalle fermé en donnant ses bornes, notées souvent a et b. On note alors [ a , b ] l'intervalle correspondant ou [ a ; b ] quand a ou b contiennent une virgule. Un intervalle centré sur c de longueur h se note c ± h/2 et correspond à [ c-h/2 , c+h/2 ]. Si on pose a=c-d et b=c+d alors on en déduit c=(a+b)/2, d = (b-a)/2 et h=b-a. Tout intervalle fermé [ a , b ] peut donc s'écrire sous la forme c ± d c'est-à-dire (a+b)/2 ± (b-a)/2.
Si on élève les deux termes de la formule au carré, alors E2=f2V/n. On en déduit donc n=f2V/E2. Comme E est inversement proportionnelle à n, il faut prendre une valeur de n supérieure ou égale à celle de l'égalité précédente pour garantir que E est inférieure ou égale à une précision donnée.
Dans le cas de l'estimation d'une proportion, f est la valeur critique z issue de la loi normale et V=p(1-p). On en déduit donc que n doit être supérieur ou égal à z2p(1-p)/E2.
Dans le cas de l'estimation d'une proportion, f est la valeur critique z issue de la loi normale (ou la valeur critique t issue de la loi de Student) et V=s2. On en déduit donc que n doit être supérieur ou égal à z2s2/E2 (ou supérieur ou égal à t2s2/E2).
Si on utilise la moyenne et l'écart-type de l'échantillon pour en déduire la moyenne et l'écart-type de la populations sous-jacente, on obtient des estimations ponctuelles. Ces valeurs, pour intéressantes qu'elles soient, ne donnent aucune idée sur la qualité de l'estimation. C'est pourquoi on utilise des intervalles de confiance afin de mieux apprécier la qualité de l'estimation et d'avoir toute une gamme de valeurs au lieu d'une seule valeur.
La théorie statistique de l'estimation fournit les formules suivantes pour les intervalles de confiance d'une proportion et d'une moyenne :
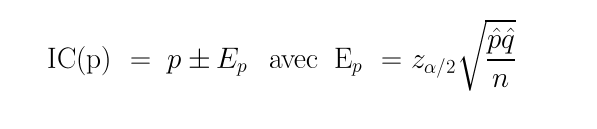
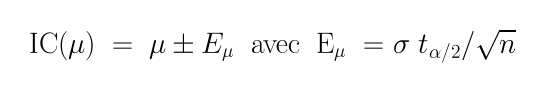
On trouvera une implémentation dans une page Web de ces formules ici. Comme ces calculs d'estimation utilisent la taille n de l'échantillon, on peut, en "retournant" ces formules, pour une précision donnée, en déduire des formules de l'estimation la taille minimale requise pour une proportion, une moyenne... On pourra en avoir une démonstration ici avec des exemples de référence.
L'erreur la plus fréquente que beaucoup de personnes font, y compris des statisticien(ne)s est de mal présenter l'interprétation d'un intervalle de confiance. Ainsi pour l'intervalle de confiance d'une moyenne à 95 %, il est faux de dire que << l'intervalle de confiance contient la moyenne de la population avec une probabilité de 0,95 >>.
Par contre, on peut dire << nous avons confiance à 95 % que cet intervalle contient la moyenne >>. Il faut comprendre que la présence de la moyenne dans l'intervalle est un fait, pas une possibilité d'évènement. Donc soit elle est dans l'intervalle, soit elle n'y est pas. Mais il n'y a aucune probabilité en jeu. Une analogie peut être celle de l'age d'un lointain cousin de votre famille : soit il a 10 ans, soit 11, soit 12... Mais il n'y a ici aucune probabilité. Par contre, vous pouvez être plus ou moins sûr, plus ou moins confiant, sur votre connaissance de l'age de l'enfant, en fonction de votre mémoire, de vos rapports avec cette famille lointaine... C'est bien pourquoi cet intervalle est nommé intervalle de confiance et non pas intervalle de présence.
Avec le logiciel R, on peut utiliser t.test pour l'intervalle de confiance d'une moyenne et binom.test ou prop.test pour l'intervalle de confiance d'une proportion.
Pour le calcul de taille d'échantillons, avec le logiciel R, on peut utiliser n.for.survey du package epiDisplay pour une proportion.
Attention : si la question sur la proportion de pois à gousses jaunes est valide, l'énoncé pour l'intervalle de confiance n'a aucun sens car le niveau de confiance pour l'intervalle n'est pas précisé. On supposera raisonnablement qu'il s'agit de 5 % pour résoudre l'exercice. Voici la solution en R si on décide de faire les calculs correspondants aux formules :
gvertes <- 428 gjaunes <- 152 nbpois <- gjaunes + gvertes propjaunes <- 100*gjaunes/nbpois cat(" Avec ",gjaunes," gousses jaunes et ",gvertes," gousses vertes, \n") cat(" il y a ",nbpois," pois en tout et ") cat(" une proportion ",propjaunes," de gousses jaunes, \n") cat(" soit, en arrondi, ",round(propjaunes)," %.\n\n") n <- nbpois p <- gjaunes/nbpois alpha <- 0.05 z <- qnorm(1-alpha/2) marge <- z*sqrt(p*(1-p)/n) pinf <- p - marge psup <- p + marge cat(" Au seuil de 5%, la valeur critique issue de la loi normale est z=",z,"\n") cat(" la marge d'erreur est ",marge,"\n et l'intervalle de confiance est donc ") ; cat(" ", p," +/-",marge,"\n") ; cat(" ou encore : ") ; cat(" ",pinf," < p < ",psup,"\n") ; cat(" soit, en arrondi, ",sprintf("%6.4f",pinf)," < p < ", sprintf("%6.4f",psup),"\n") ;Et ses résultats :
Avec 152 gousses jaunes et 428 gousses vertes, il y a 580 pois en tout et une proportion 26.20690 de gousses jaunes, soit, en arrondi, 26 %. Au seuil de 5%, la valeur critique issue de la loi normale est z= 1.959964 la marge d'erreur est 0.03578902 et l'intervalle de confiance est donc 0.2620690 +/- 0.03578902 ou encore : 0.2262799 < p < 0.297858 soit, en arrondi, 0.2263 < p < 0.2979On pourra vérifier qu'on trouve les mêmes valeurs avec les expressions suivantes qui utilisent des fonctions de R qui implémentent les calculs des intervalles de confiance :
binom.test( 152 , 580 , 0.2620690) prop.test( 152 , 580 , 0.2620690) icp(580 , 0.262)La dernière foncion, icp est une des fonctions que nous avons écrites, qui affiche des résultats en français. Elle est chargeable, comme nos autres fonctions, par :
# lecture sur internet source("http://forge.info.univ-angers.fr/~gh/wstat/statgh.r",encoding="latin1") ## lecture en local sur le disque D: (Windows) ## source("D:/statgh.r") ## lecture sur en local sur /home/cours/ (Linux) ## source("/home/cours/statgh.r",encoding="latin1")Voici les résultats de la vérification :
# résultats de binom.test( 152 , 580 , 0.2620690) Exact binomial test data: 152 and 580 number of successes = 152, number of trials = 580, p-value = 1 alternative hypothesis: true probability of success is not equal to 0.262069 95 percent confidence interval: 0.2267068 0.2998745 sample estimates: probability of success 0.2620690 # résultats de prop.test( 152 , 580 , 0.2620690) 1-sample proportions test with continuity correction data: 152 out of 580, null probability 0.262069 X-squared = 0, df = 1, p-value = 1 alternative hypothesis: true p is not equal to 0.262069 95 percent confidence interval: 0.2279290 0.2993399 sample estimates: p 0.2620690 # résultats de icp(580 , 0.262) [1] 0.226214 0.297786 # résultats de icp(580 , 0.262, 0.05, TRUE) Pour 580 et une proportion estimée p-chapeau 0.262 au niveau 0.05 la valeur critique issue de la loi normale est 1.959964 soit 1.960 l'intervalle de confiance est donc sans doute [ 0.226214 ; 0.297786 ] soit, en arrondi, [ 0.226 ; 0.298 ] [1] 0.226214 0.297786Là encore, l'énoncé n'a aucun sens car le niveau de confiance pour la marge d'erreur n'est pas précisé. On supposera raisonnablement qu'il s'agit de 5 %. Voici la solution en R :
p <- 0.5 # hypothèse "maximale", aucune probabilité précédente points <- 4 alpha <- 0.05 z <- qnorm(1-alpha/2) marge <- points/100 n <- z^2*p*(1-p)/marge^2 nok <- 1 + round(n) cat("n vaut au moins ",n,"\n") cat("il faudra donc certainement interroger ",nok," femmes\n")Et ses résultats :
n vaut au moins 600.228 il faudra donc certainement interroger 601 femmesSi on sait que la proportion est p=0,169 on peut utiliser cette valeur au lieu de l'hypothèse maximale p=0,5 et on trouve alors qu'il faut interroger 338 femmes. Ce nombre est bien sûr plus petit puisque le calcul précédent était une hypothèse avec un minimum d'information.
Qu'il s'agisse de femmes françaises ou de femmes américaines n'influe pas : la taille de l'échantillon est liée à la précision voulue mais pas à la taille de la population sous-jacente.
Voici les calculs sous R :
cat(" CALCULS DETAILLES \"A LA MAIN\" \n") ; # taux d'urée d'une population # valeurs fournies nbind <- 100 # individus sdval <- 4000 # somme des valeurs (en mg/l) sdcar <- 166336 # somme des carrés des valeurs # calculs pour l'échantillon moy <- sdval/nbind moycar <- sdcar/nbind vari <- moycar -moy*moy ect <- sqrt( vari ) cat(" Moyenne échantillon",moy," mg/l\n") ; # calculs pour la population moy <- sdval/nbind moycar <- sdcar/nbind vari <- (moycar -moy*moy)*nbind/(nbind-1) ect <- sqrt( vari ) cat(" Moyenne estimée de la population",moy," mg/l\n") ; cat(" Ecart-type estimé de la population",ect," mg/l\n") ; # variance et écart-type de la moyenne varimoy <- vari/nbind ectmoy <- sqrt(varimoy) cat(" Variance de la moyenne ",varimoy," mg/l\n") ; cat(" Ecart-type de la moyenne ",ectmoy," mg/l\n") ; cat(" (nommé aussi erreur type ou \"se\" ou erreur standard)\n") ; # Intervalle de confiance à 95 % puis à 99 % du taux d'urée deg <- 5 alp <- (deg/100)/2 aln <- qnorm(1-alp) margeE <- aln*ect/sqrt(nbind) liminf <- moy - margeE limsup <- moy + margeE cat(" Intervalle urée à ",100-deg," % : [ ",liminf," , ",limsup," ]\n") ; deg <- 1 alp <- (deg/100)/2 aln <- qnorm(1-alp) margeE <- aln*ect/sqrt(nbind) liminf <- moy - margeE limsup <- moy + margeE cat(" Intervalle urée à ",100-deg," % : [ ",liminf," , ",limsup," ]\n") ; # intervalles de confiance cat(" INTERVALLES DE CONFIANCE, CALCULS AVEC DES FONCTIONS gh \n") ; cat("Intervalle à 95 % : ",icm(nbind,moy,ect),"\n") ; cat("Intervalle à 99 % : ",icm(nbind,moy,ect,0.01,TRUE),"\n")Et leurs résultats :
CALCULS DETAILLES "A LA MAIN" Moyenne échantillon 40 mg/l Ecart-type échantillon 7.9599 mg/l Moyenne estimée de la population 40 mg/l Ecart-type estimé de la population 8 mg/l Variance de la moyenne 0.64 mg/l Ecart-type de la moyenne 0.8 mg/l (nommé aussi erreur type ou "se" ou erreur standard) Intervalle urée à 95 % : [ 38.43203 , 41.56797 ] Intervalle urée à 99 % : [ 37.93934 , 42.06066 ] INTERVALLES DE CONFIANCE, CALCULS AVEC DES FONCTIONS gh Intervalle à 95 % : 38.41263 41.58737 Pour 100 valeurs de moyenne 40 et d'écart-type 8 au niveau 0.01 la valeur critique issue de la loi du t de Student pour 99 ddl est 2.626405 soit en arrondi 2.626 l'intervalle de confiance est donc sans doute [ 37.89888 ; 42.10112 ] soit, en arrondi, [ 37.899 ; 42.101 ] Intervalle à 99 % : 37.89888 42.10112L'intervalle à 99 % est plus grand que celui à 95 % car pour être plus sûr d'encadrer la moyenne, il faut prendre un intervalle plus grand. A la limite, pour une précision infinie, soit icm(100,40,8,0.00) on trouve l'intervalle de confiance [ -Inf , Inf ] qui va de moins l'infini à plus l'infini !
La taille d'échantillon doit être d'au moins 16 personnes. Détail des calculs volontairement non fourni.
Voir notre page courte et notre page longue sur les tests pour une introduction à la méthodologie des tests et pour une liste de tests. Voici le rappel succinct des étapes d'un test statistique :
A partir d'une hypothèse métier (biologique), on écrit une hypothèse statistique nulle et l'hypothèse alternative. On choisit alors un test adapté à la distribution des données et on en déduit la loi de la statistique de test. On décide ensuite du résultat du test à l'aide de la ou des valeurs critiques issues du niveau de confiance ou en utilisant l'intervalle de confiance de la statistique de test. Enfin, on rédige la conclusion en termes métier.
Il faut faire attention aux conditions d'applications des tests. Certains s'appliquent à des données appariées et d'autres non. Certains requièrent la normalité des variables QT, d'autres non. On pourra relire les trois premiers exercices de notre séance 2 en master BTV et leurs solutions pour un rappel de ces distinctions.
On trouvera une bonne introduction à l'inférence statistique dans le cours06 de Pierre Legendre. et Daniel Borcard dont une copie locale est ici.
Pour réviser tout ce qui a été vu jusqu'ici, on lira aussi avec profit R pour Statophobes Denis POINSOT, qui fait suite à Statistiques pour statophobes dont les copies locales sont ici et là. Enfin, la présentation et la rédaction pour les tests de Christian Jost, dans le fichier PDF (copie locale) se révélera très instructive pour qui n'a jamais rédigé de telles analyses statistiques.
Concernant l'application qui consiste à calculer un test t sur la première colonne des données iris, on sera très "méfiant(e)" car l'énoncé propose juste un calcul à effectuer.
On ne sait pas ce qu'on veut obtenir. S'agit-il d'avoir juste l'intervalle de confiance de la moyenne dans la mesure où la fonction t.test() renvoie ce résultat ? Est-ce un "piège" puisqu'il faut en principe regarder la distribution avant de choisir un test paramétrique ou non paramétrique ? Enfin, est-ce une "erreur" puisqu'on ne connait même pas le nom de la colonne à traiter, ni son unité ? Toutes ces questions montrent que l'on a raison d'être "circonspect(e)".
En admettant qu'un énoncé plus précis ait justifié d'analyser la variable Longeur des sépales exprimée en centimètres à l'aide d'un test t, les résultats fournis, reproduits ci-dessous, montrent que la moyenne des longueurs, égale à environ 8,84 cm est significativement différente de zéro, au seuil de 5 % puisque la p-value est de l'ordre de 2 fois dix puissance moins 16.
One Sample t-test data: iris[, 1] t = 86.4254, df = 149, p-value < 2.2e-16 alternative hypothesis: true mean is not equal to 0 95 percent confidence interval: 5.709732 5.976934 sample estimates: mean of x 5.843333
Retour à la page principale de (gH)