Découpage en classes et discrétisation
Plan de la page
1. Définition
2. Exemple introductif
3. Qu'est-ce qu'une "bonne" discrétisation ?
4. Comment choisir le nombre de classes ?
5. Comment choisir les bornes de classes ?
5.1 la méthode des quantiles ("des effectifs égaux")
5.2 la méthode des amplitudes
5.3 la méthode des moyennes emboitées
5.4 la méthode des grandes différences relatives
6. Comment nommer les classes ?
7. Comparaison de découpages et validation du nombre de classes
8. Programmes associés
1. Définition
Discrétiser une variable quantitative c'est, mathématiquement, transformer un vecteur de nombres réels en un vecteur de nombres entiers nommés "indices de classe". C'est pourquoi cette effectuer cette transformation se dit en langage courant "réaliser un découpage en classes". En statistiques, discrétiser c'est à la fois réaliser cette transformation mathématique, nommer et justifier les classes.
2. Exemple introductif
Prenons un exemple (fictif) de 30 individus, définis par un identificateur et une taille exprimée en centimètres :
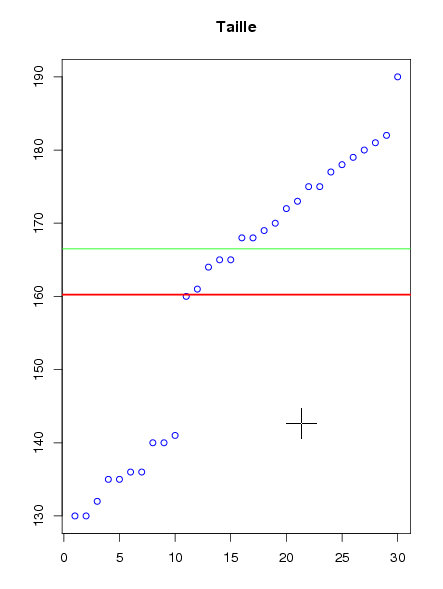
ID TAILLE P01 130 P02 140 G01 170 G02 160 P03 136 G03 165 P04 130 P05 135 P06 140 P07 135 G04 161 P08 136 G05 180 G06 190 P09 141 P10 132 G07 165 G08 168 G09 182 G10 177 G11 172 G12 168 G13 175 G14 181 G15 173 G16 169 G17 178 G18 179 G19 175 G20 164Pour avoir une idée des données donc des classes à définir, on peut calculer les résumés statistiques classiques liés à une variable quantitative et tracer les données rangées par ordre croissant. Une analyse statistique chiffrée n'est pas toujours aussi parlante qu'un simple graphique pour trouver comment définir les classes comme on peut le voir ci-dessous. L'image est cliquable ; la moyenne est en rouge, la médiane en vert.
Un logiciel de statistiques comme Rstat détecte avec sa fonction "cut" deux classes et propose comme bornes de classes les valeurs
Classe 1 : [130,160] Classe 2 : ]160,190]On en déduit donc les deux classes :Numéro | Classe 1 | Classe 2 | | 01 | P01 130 | G04 161 02 | P04 130 | G20 164 03 | P10 132 | G03 165 04 | P05 135 | G07 165 05 | P07 135 | G08 168 06 | P03 136 | G12 168 07 | P08 136 | G16 169 08 | P02 140 | G01 170 09 | P06 140 | G11 172 10 | P09 141 | G15 173 11 | G02 160 | G13 175 12 | | G19 175 13 | | G10 177 14 | | G17 178 15 | | G18 179 16 | | G05 180 17 | | G14 181 18 | | G09 182 19 | | G06 190A la suite de cette transformation mathématique, le statisticien rajoutera : la classe 1 est celle des "petits" et la classe 2 celle des "grands".
Remarque : G02, dernier individu de la classe 1 est sans doute mal classé car il est plus proche de G04 (premier élément de la classe 2) que de P09, avant-dernier individu de la classe 1 ...
3. Qu'est-ce qu'une "bonne" discrétisation ?
Pour réaliser une discrétisation, il faut choisir le nombre de classes et les bornes de classe. Pour réaliser une bonne discrétisation, il faut justifier à la fois le nombre de classes et les bornes de classe, le terme "bonne" faisant référence à des critères explicitement définis. Intuitivement, un bon découpage correspond à des classes homogènes et séparées, ce qui correspond respectivement aux notions statistiques de faible variance intraclasse et de forte variance interclasse. Mais d'autres critères sont possibles, comme l'équirépartition, le respect d'un nombre minimal de données par classe etc.
Ainsi sur l'exemple précédent, il y a intuitivement 2 classes, celle des petits (moins de 150 cm) et celle des grands (plus de 150 cm). Le découpage proposé par Rstat, basé sur la médiane est "incorrect" alors qu'avec G02 en classe 2 on obtient "un meilleur découpage" :
On comparera ces diverses valeurs avec l'étude globale de l'ensemble des valeurs :
Découpage proposé par Rstat =========================== Etude de la classe 1 Nombre d'éléments : 11 Moyenne : 137.727 cm Variance : 62.744 Ecart-type : 7.921 cm Coeff. de variation : 5.751 % Centre de gravité : 137.727 cm Inertie : 690.182 Etude de la classe 2 Nombre d'éléments : 19 Moyenne : 173.263 cm Variance : 52.404 Ecart-type : 7.239 cm Coeff. de variation : 4.178 % Centre de gravité : 173.263 cm Inertie : 995.684 Décomposition de l'Inertie Totale = intra + inter 10483.37 = 1685.87 + 8797.50Découpage amélioré avec G02 en classe 2 ======================================= Etude de la classe 1 Nombre d'éléments : 10 Moyenne : 135.500 cm Variance : 14.450 Ecart-type : 3.801 cm Coeff. de variation : 2.805 % Centre de gravité : 135.500 cm Inertie : 144.500 Etude de la classe 2 Nombre d'éléments : 20 Moyenne : 172.600 cm Variance : 58.140 Ecart-type : 7.625 cm Coeff. de variation : 4.418 % Centre de gravité : 172.600 cm Inertie : 1162.800 Décomposition de l'Inertie Totale = intra + inter 10483.37 = 1307.30 + 9176.07Nombre d'éléments : 30 Moyenne : 160.233 cm Variance : 349.446 Ecart-type : 18.693 cm Coeff. de variation : 11.666 % Centre de gravité : 160.233 cm Inertie : 10483.3674. Comment choisir le nombre de classes ?
Il existe quelques formules "toute faites" pour déterminer à l'aveugle le nombre n de classes à partir du nombre N de données :
Brooks-Carruthers 5*log(N,base=10) Huntsberger 1 + 3,332*log(N,base=10) Sturges log(N+1,base=2)Deux autres formules, censées être plus précises, mettent en jeu le minimum a des données et le maximum b et utilisent aussi d'autres paramètres de la dispersion : sig, l'écart-type et eiq l'écart inter-quartiles :
Scott (b-a)/(3.5*sig*N**(-1/3)) Freedman-Diaconis (b-a)/(2*eiq*N**(-1/3))Malheureusement aucune de ces formules ne donne le "bon" nombre de classes pour notre exemple :
Formule n (nombre de classes non arrondi) Sturges Log 10 / Huntsberger 5.922 Sturges Log 2 4.954 Scott W 2.802 Freedman-Diaconis W 2.663 Brooks-Carruthers 7.386Une méthode pour obtenir des classes bien séparées, à défaut d'être homogènes, consiste à programmer un algorithme adaptatif qui utilise les différences relatives entre valeurs consécutives triées comme par exemple notre implémentation nommée GDR. Malheureusement, un tel algorithme demande de choisir un seuil de séparation entre différences relatives et introduit aussi un certain arbitraire. On peut essayer d'éliminer cet arbitraire en utilisant différents seuils "raisonnables" et en gardant le nombre de classes le plus fréquent...
Deux remarques pour conclure sur la détermination (ou le choix) du nombre de classes : certaines méthodes -- dont celle des moyennes emboitéees -- requièrent que le nombre de classes soit une puissance de deux ; pour des raisons d'homogénéité avec les autres variables qualitatives de l'étude, on peut être amené à choisir un nombre de classes différent de celui qu'on pourrait considérer comme optimal si les données étaient traitées seules.
5. Comment choisir les bornes de classes ?
Il existe de nombreuses méthodes, dont la plupart ont des critères explicites de découpage et des formules mathématiques pour calculer les bornes. La plupart de ces méthodes suppose que le nombre de classes a été fixé. Nous ne présentons ici que quelques méthodes.
5.1 La méthode des quantiles ("des effectifs égaux")
Le critère visé est l'équirépartition, c'est à dire le même nombre de données par classe. Dans la version stricte, à partir du nombre du nombre N de données et du nombre n classes, on en déduit le nombre F d'individus par classe. On trie les données par ordre croissant et on met dans la classe 1 les F premières données, dans la classe 2 les F suivantes etc. Dans la version relâchée, on met éventuellement plus de F données par classe car on force les données égales à être dans une même. Voici ce que cela donne sur un exemple de 6 valeurs avec 2 classes :
Données : 10 11 12 12 13 14 Version stricte : 1 1 1 2 2 2 Version relâchée : 1 1 1 1 2 25.2 La méthode des amplitudes
On garantit ici que le critère d'égalité d'amplitude de classe est respecté, l'amplitude étant la différence entre la plus grande valeur et la plus petite valeur. A partir du minimum global a des données et du maximum global b des données on calcule les bornes de classe hi à l'aide d'une simple progression arithmétique dont la raison est k=(b-a)/(n-1). Une variante de cette méthode consiste à prendre comme largeur k la valeur de l'écart-type des données. Si n est impair, la classe du milieu a pour bornes m-k/2,m+k/2 où m est la moyenne des données. Si n est pair, m est la borne supérieure de la classe numéro n/2.
5.3 La méthode des moyennes emboitées
Le nombre de classes est ici une puissance de deux. On sépare l'intervalle de départ en deux en prenant comme valeur de séparation la moyenne globales des valeurs. On recommence ensuite en découpant chaque classe en deux en prenant comme comme valeur de séparation la moyenne des valeurs de la classe.
5.4 La méthode des grandes différences relatives
On trie les valeurs par ordre croissant puis on calcule les différences relatives successives entre une valeur et sa suivante. On change de classe lorsque la différence relative est supérieure à un seuil arbitraire, classiquement 50 %. Le nombre de classes n'est donc pas fixé a priori. Voir la page GDR qui lui est consacrée.
6. Comment nommer les classes ?
Cette dernière opération, souvent omise en mathématiques, est obligatoire et fondamentale en statistiques. Le choix des termes est trés important car lorsqu'on étudie les classes, on fera référence aux noms des classes et non à leur numéro. Un découpage en classes de l'age qui aboutit à une classe de "jeunes" et une classe de "vieux" ne véhicule pas la même information qu'un découpage en "juvéniles" et "séniles", ou en "précoces" et "tardifs".
Pour bien nommer, il faut d'abord beaucoup de vocabulaire et ensuite pas mal de sémantique. Des dictionnaires de synonymes sont donc des aides précieuses ainsi que des dictionnaires encyclopédiques voire étymologiques. Le choix des termes doit se faire en fonction du contexte mais aussi en fonction du destinataire du rapport d'étude. Ainsi le terme "juvénile" sera moins bien compris que "jeune" par le "grand public".
7. Comparaison de découpages et validation du nombre de classes
Pour comparer des découpages en classes, il existe de nombreux indices dont les plus fiables sont sans doute les indices F, indice W (Wilks) et D (Davies-Bouldin), qui mettent en jeu
- n, le nombre de données
- k le nombre de classes
- B l'inertie inter ("between")
- W l'inertie intra ("within")
- ni, nombre d'élements de la classe i
- gi, le centre de gravité de la classe i
- ...
Pour les indices F et W, le découpage de plus fort indice est considéré comme le meilleur alors que pour l'indice D, le découpage de plus faible indice est considéré comme le meilleur.
Une méthode de validation du meilleur nombre de classes consiste alors à vérifier que le nombre de classes choisi maximise bien F et W et qu'il minimise D. On peut aussi s'en servir comme méthode de détermination du meilleur nombre de classes en comparant tous les découpages en k classes, k de 2 à P où P est un nombre entier considéré comme le un nombre maximum plausible de classes.
Le texte de référence qui détaille ces formules dans le cadre des comparaisons de partitions -- le résultat de la discrétisation étant une partition des individus -- est la thèse de G. Youness dont une copie locale est rc898.pdf.
8. Programmes associés
Diagramme en tige et feuille d'une variable quantitative
Découpages en classes et indices de comparaison (projet étudiant)
Grandes Différences Relatives
 Retour à la page principale de
(gH)
Retour à la page principale de
(gH)