1. Notion de régression (simple, multiple, linéaire, logistique)
Comment effectue-t-on une régression en R ? Quelles sont les principales fonctions génériques ?
Pour réaliser une régression linéaire en R, on utilise la fonction lm avec l'opérateur ~ (tilde) alors qu'une régression logistique passe par la fonction glm.
La fonction lm renvoie une liste avec entre autres les variables suivantes :
| $coefficients |
estimation des coefficients |
| $fitted.values |
les valeurs calculées pour chaque y |
| $residuals |
les résidus (différences entre valeurs originales et valeurs estimées) |
Si on écrit print(ml) où ml est le résultat d'une fonction lm ou glm, on n'obtient que les coefficients de la régression. Pour avoir le détail de la régression, il faut utiliser summary(ml) et confint(ml) pour avoir les intervalles de confiance des coefficients de la régression. Les fonctions correspondantes sont : summary.lm et summary.glm car summary est une fonction générique qui peut s'appliquer à de nombreux objets. On peut ensuite prédire de nouvelles valeurs avec la fonction predict qui est une aussi fonction générique qui se décline en predict.lm et predict.glm.
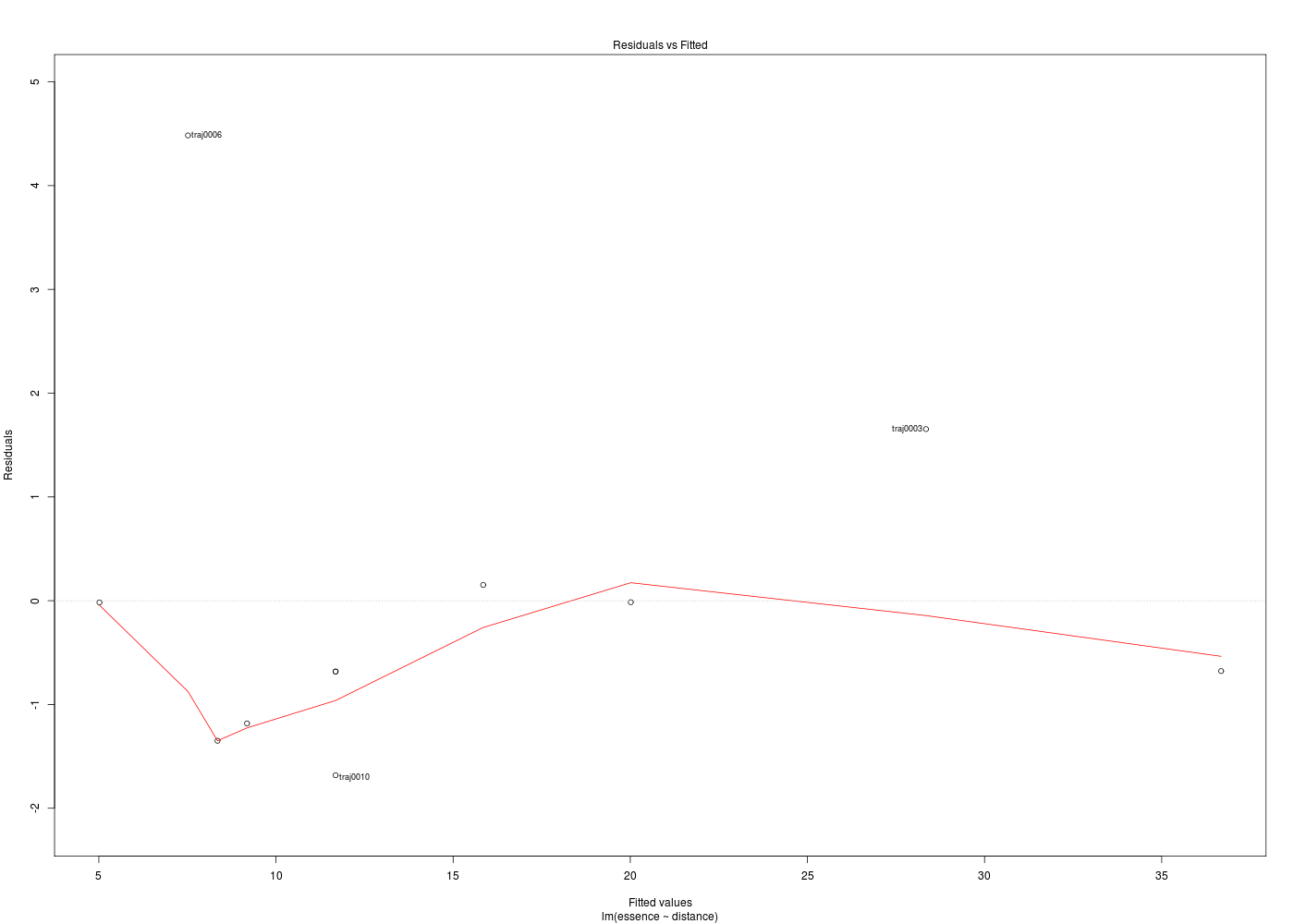
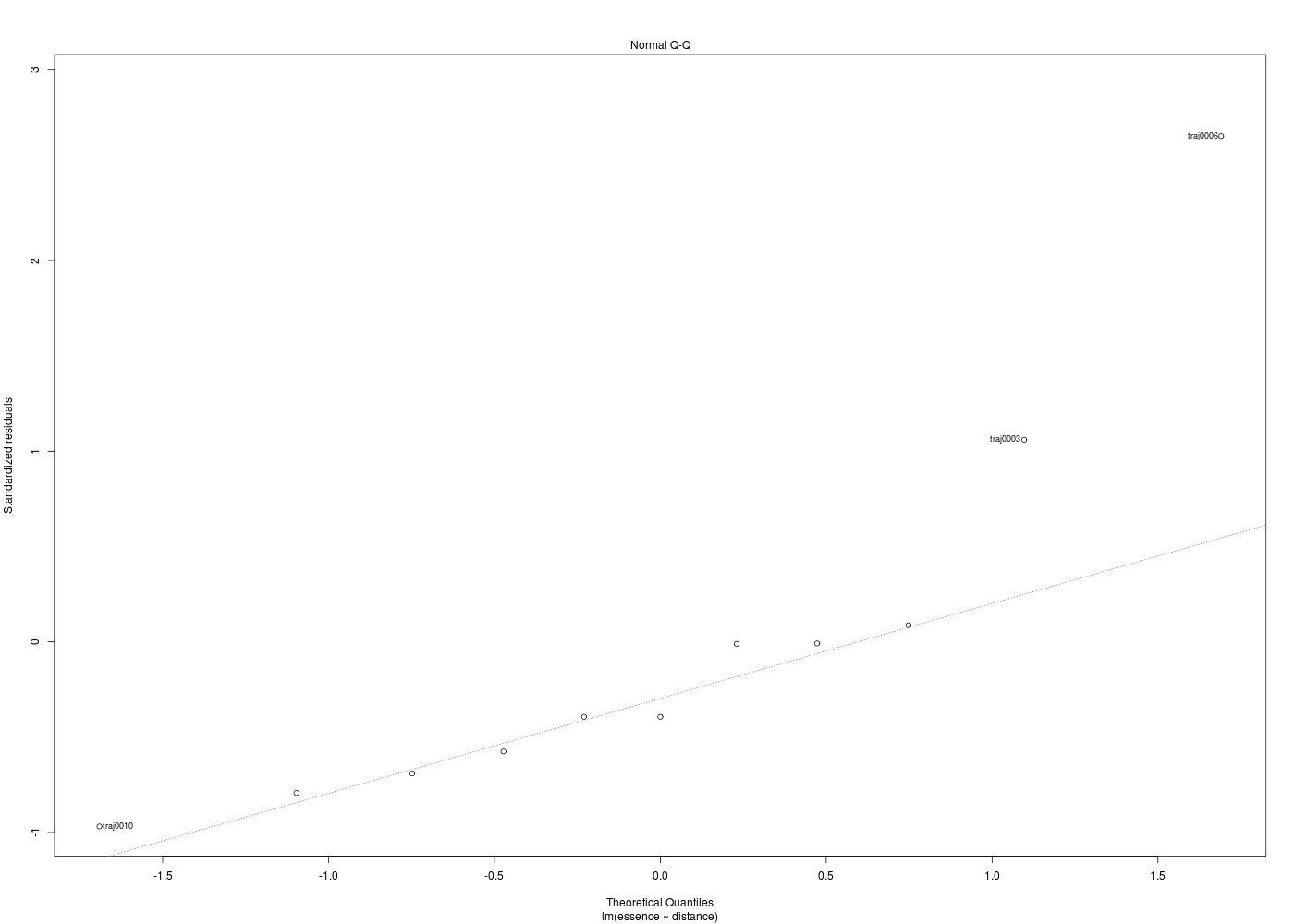
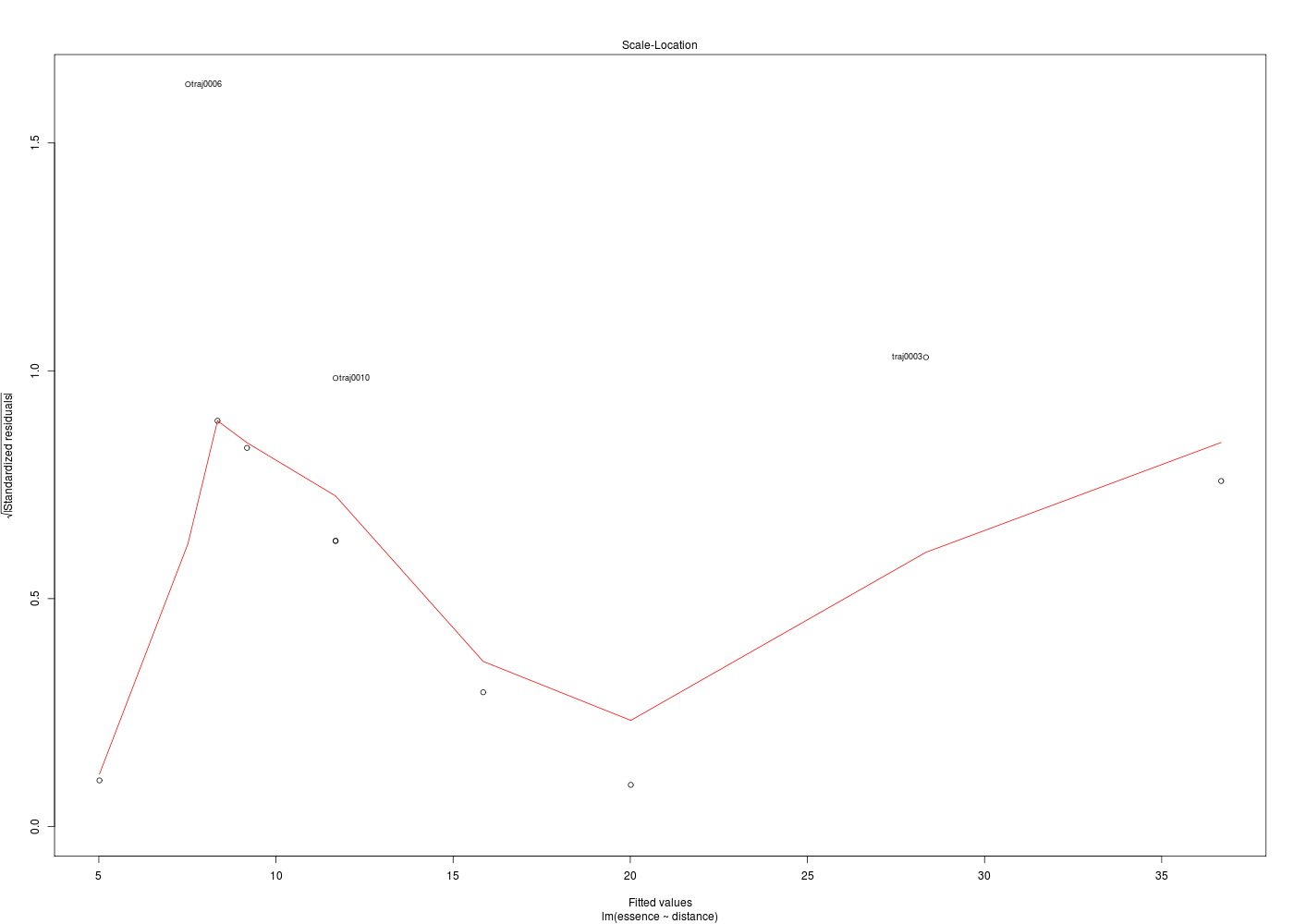
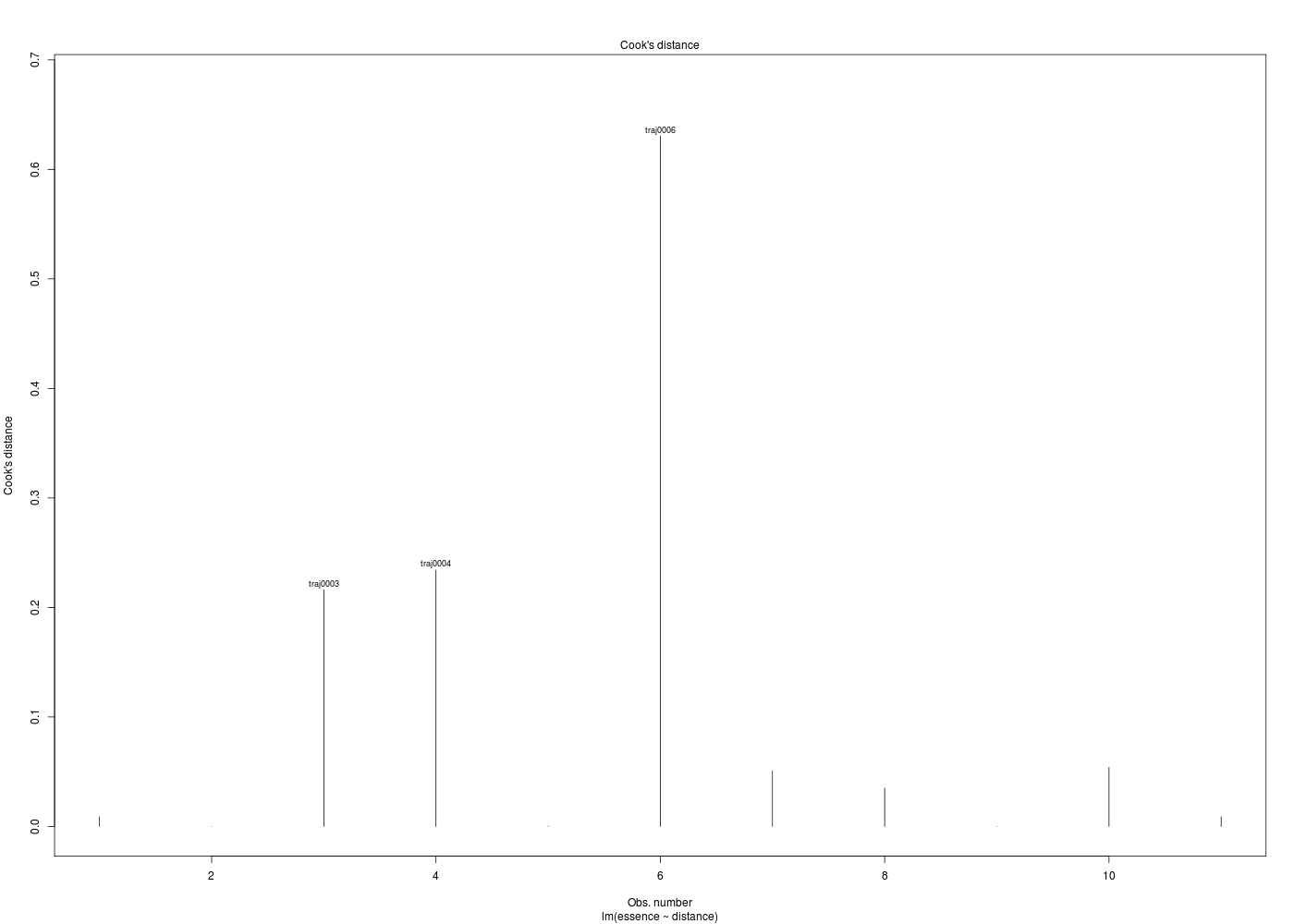
La partie graphique est très importante pour les régressions. Pour une régression linéaire, après un plot élémentaire des données, un abline du modèle trace la droite de régression. A la suite d'une régression, la fonction plot.lm produit 6 graphiques pour analyser la qualité de la régression, dont seuls 4 sont affichés par défaut, repérés ci-dessous par une étoile :
| |
x |
y |
| 1 |
* Fitted values |
Residuals |
| 2 |
* Theoretical quantiles |
Standardized residuals |
| 3 |
* Fitted values |
Root of standardized residuals |
| 4 |
Observation number |
Cook's distance |
| 5 |
* Leverage |
Standardized residuals |
| 6 |
Leverage hn |
Cook's distance |
Enfin, signalons qu'avec predict et matlines il est possible de tracer l'intervalle de confiance de la droite et l'intervalle de confiance des prévisons.
2. Régression linéaire simple
Après avoir vu la documentation de la fonction lm() du package stats essayer de réaliser la modélisation par une relation linéaire la dépendance entre la variable consommation d'essence et la variable distance parcourue dans le jeu de données km.dar (sans transformation des données).
Dans quel ordre doit-on lire les résultats ? Faut-il regarder en premier le R2, la p-value de F, les coefficients ?
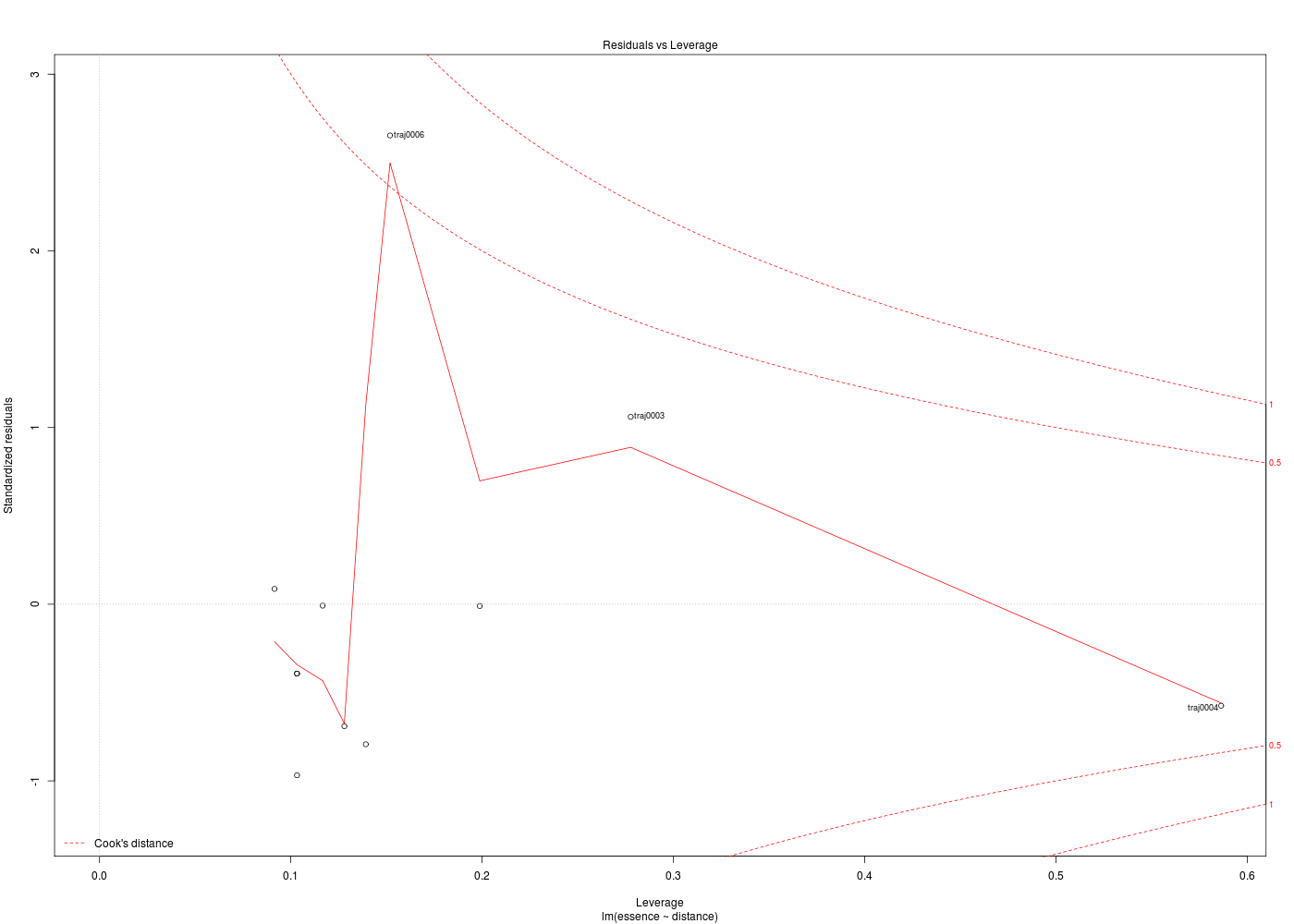
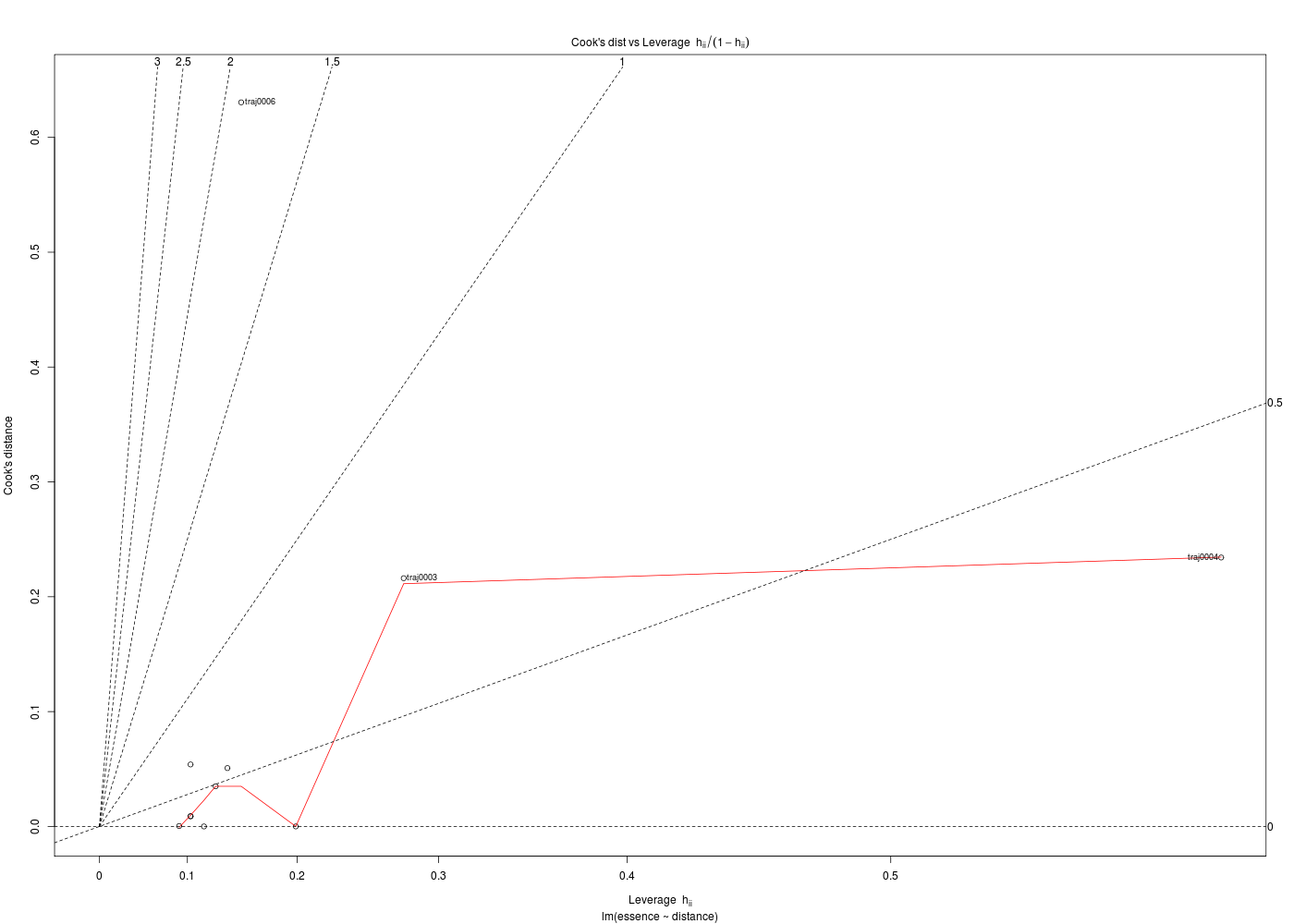
Y a-t-il des représentations graphiques associées ? Pourquoi y a-t-il 4 graphiques produits avec plot(lm(modele)) alors qu'on pourrait en avoir 6 ? Comment obtenir les 6 tracés ? A quoi correspondent-ils ?
Faut-il envisager une relation de causalité ? Quelles sont les valeurs prédites par le modèle pour 100 et 250 km ? Quelle est l'augmentation de la consommation si la distance augmente de 1 km ?
Rappel : pour définir un modèle linéaire avec R, il faut utiliser la fonction lm() et la droite correspondante se trace directement avec abline(). Pour afficher le modèle, on peut utiliser les fonctions génériques summary() et coef().
# chargement des fonctions (gH)
source("http://forge.info.univ-angers.fr/~gh/wstat/statgh.r",encoding="latin1")
# lecture des données (enregistrées en local)
km <- lit.dar("km.dar")
# lecture des données sur internet
# km <- lit.dar("http://forge.info.univ-angers.fr/~gh/wstat/Eda/km.dar")
idx <- order(km$distance)
# tracé rapide
# surtout pas
# with( km, plot(essence~distance,type="b") )
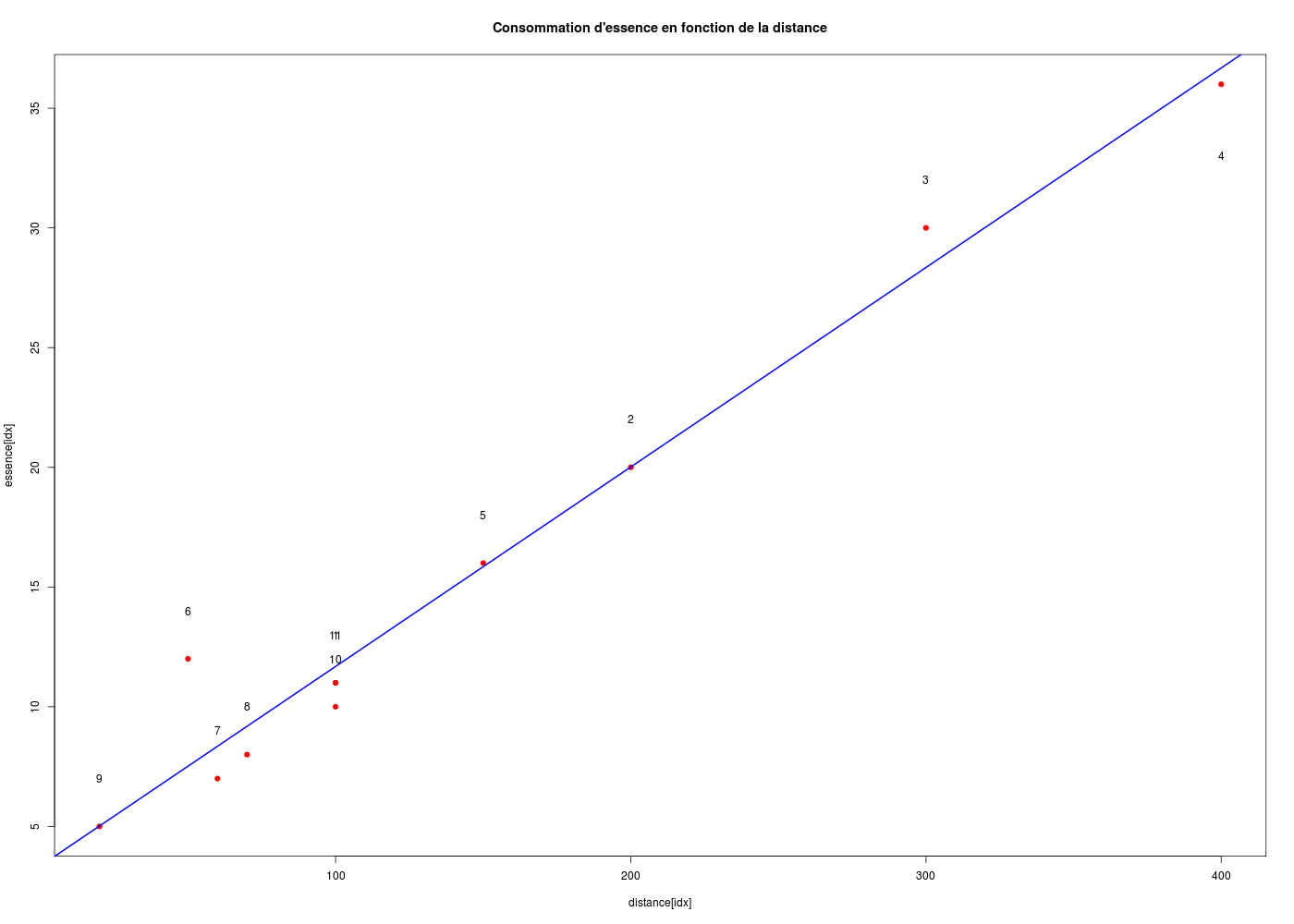
with( km, plot(essence[idx]~distance[idx],type="p",pch=19,col="red" ))
# ajout de la droite de régression et un titre
ml <- lm(essence ~ distance,data=km) # pas besoin de idx ici
abline(ml, col="blue",lwd=2)
title("Consommation d'essence en fonction de la distance")
# affichons le nom des points
text(x=km$distance,y=km$essence+2,label=1:nrow(km))
# oups, le point 4 déborde, ajoutons-le
text(x=400,y=33,label="4")
# description du modèle
cats("Modèle linéaire ESSENCE en fonction de DISTANCE")
print( summary(ml) )
cats("ANOVA de ce modèle")
print( anova(ml) )
# coefficients
cats("coefficients seulement")
print( coef(ml) )
# l'objet issu de lm est complexe
cats("Objet modèle linéaire :")
print( names(ml) )
print( str(ml) )
Modèle linéaire ESSENCE en fonction de DISTANCE
===============================================
Call:
lm(formula = essence ~ distance, data = km)
Residuals:
Min 1Q Median 3Q Max
-1.6824 -0.9326 -0.6783 0.0686 4.4836
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.350376 0.894150 3.747 0.00458 **
distance 0.083320 0.004985 16.714 4.39e-08 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.835 on 9 degrees of freedom
Multiple R-squared: 0.9688, Adjusted R-squared: 0.9653
F-statistic: 279.4 on 1 and 9 DF, p-value: 4.393e-08
ANOVA de ce modèle
==================
Analysis of Variance Table
Response: essence
Df Sum Sq Mean Sq F value Pr(>F)
distance 1 940.61 940.61 279.36 4.393e-08 ***
Residuals 9 30.30 3.37
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
coefficients seulement
======================
(Intercept) distance
3.35037574 0.08331991
Objet modèle linéaire :
=======================
[1] "coefficients" "residuals" "effects" "rank" "fitted.values" "assign" "qr" "df.residual" "xlevels" "call" "terms"
[12] "model"
List of 12
$ coefficients : Named num [1:2] 3.3504 0.0833
..- attr(*, "names")= chr [1:2] "(Intercept)" "distance"
$ residuals : Named num [1:11] -0.6824 -0.0144 1.6537 -0.6783 0.1516 ...
..- attr(*, "names")= chr [1:11] "traj0001" "traj0002" "traj0003" "traj0004" ...
$ effects : Named num [1:11] -50.051 -30.669 1.756 -0.609 0.304 ...
..- attr(*, "names")= chr [1:11] "(Intercept)" "distance" "" "" ...
$ rank : int 2
$ fitted.values: Named num [1:11] 11.7 20 28.3 36.7 15.8 ...
..- attr(*, "names")= chr [1:11] "traj0001" "traj0002" "traj0003" "traj0004" ...
$ assign : int [1:2] 0 1
$ qr :List of 5
..$ qr : num [1:11, 1:2] -3.317 0.302 0.302 0.302 0.302 ...
.. ..- attr(*, "dimnames")=List of 2
.. .. ..$ : chr [1:11] "traj0001" "traj0002" "traj0003" "traj0004" ...
.. .. ..$ : chr [1:2] "(Intercept)" "distance"
.. ..- attr(*, "assign")= int [1:2] 0 1
..$ qraux: num [1:2] 1.3 1.19
..$ pivot: int [1:2] 1 2
..$ tol : num 1e-07
..$ rank : int 2
..- attr(*, "class")= chr "qr"
$ df.residual : int 9
$ xlevels : Named list()
$ call : language lm(formula = essence ~ distance, data = km)
$ terms :Classes 'terms', 'formula' length 3 essence ~ distance
.. ..- attr(*, "variables")= language list(essence, distance)
.. ..- attr(*, "factors")= int [1:2, 1] 0 1
.. .. ..- attr(*, "dimnames")=List of 2
.. .. .. ..$ : chr [1:2] "essence" "distance"
.. .. .. ..$ : chr "distance"
.. ..- attr(*, "term.labels")= chr "distance"
.. ..- attr(*, "order")= int 1
.. ..- attr(*, "intercept")= int 1
.. ..- attr(*, "response")= int 1
.. ..- attr(*, ".Environment")=<environment: R_GlobalEnv>
.. ..- attr(*, "predvars")= language list(essence, distance)
.. ..- attr(*, "dataClasses")= Named chr [1:2] "numeric" "numeric"
.. .. ..- attr(*, "names")= chr [1:2] "essence" "distance"
$ model :'data.frame': 11 obs. of 2 variables:
..$ essence : int [1:11] 11 20 30 36 16 12 7 8 5 10 ...
..$ distance: int [1:11] 100 200 300 400 150 50 60 70 20 100 ...
..- attr(*, "terms")=Classes 'terms', 'formula' length 3 essence ~ distance
.. .. ..- attr(*, "variables")= language list(essence, distance)
.. .. ..- attr(*, "factors")= int [1:2, 1] 0 1
.. .. .. ..- attr(*, "dimnames")=List of 2
.. .. .. .. ..$ : chr [1:2] "essence" "distance"
.. .. .. .. ..$ : chr "distance"
.. .. ..- attr(*, "term.labels")= chr "distance"
.. .. ..- attr(*, "order")= int 1
.. .. ..- attr(*, "intercept")= int 1
.. .. ..- attr(*, "response")= int 1
.. .. ..- attr(*, ".Environment")=<environment: R_GlobalEnv>
.. .. ..- attr(*, "predvars")= language list(essence, distance)
.. .. ..- attr(*, "dataClasses")= Named chr [1:2] "numeric" "numeric"
.. .. .. ..- attr(*, "names")= chr [1:2] "essence" "distance"
- attr(*, "class")= chr "lm"
NULL
Il est d'usage de commencer par regarder si le modèle est significativement différent de zéro dans les sorties de summary() grâce à la p-value du test de Fisher. Si cette p-value est supérieure à 0,05 «le modèle ne vaut rien». Si le modèle est significativement différent de zéro, on peut s'intéresser directement au coefficient de détermination en régression linéaire simple. Par contre en régression linéaire multiple, il faut regarder les p-values des coefficients pour envisager une sélection de variables avant d'utiliser le coefficient de détermination ajusté.
Ici, le modèle est significativement différent de zéro (p=4.393e-08<<0,05) et on peut donc dire ici que la consommation est d'environ 0,08332 litre par km, ou, pour parler plus couramment, d'environ 8,332 litre "aux 100". Donc si la distance augmente d'un km, la consommation augmente de 0,008332 litre. Par contre il ne faut pas mésestimer le terme constant, soit ici 3,53 l qui doit correspondre au premier démarrage de la voiture (il s'agit de ma propre voiture, une XM et il ne faut pas rouler tant que le systéme hydraulique n'est pas opérationnel, donc tant que la voiture n'est pas en "position haute", ce qui dure au moins 30 secondes...) et à la consommation pendant l'arrêt. Cette constante sera d'autant plus importante que la distance est effectuée en ville, à cause des stops et des feux rouges, mais il est clair que ces interprétations ne sont pas statistiques et font appel à des connaissances contextuelles liées aux données. Le modèle est un "très bon modèle" puisque le coefficient de détermination vaut 0.97 (donc très proche de 1).
Dans la mesure où un modèle linéaire est [presque] toujours calculable, il est important de savoir si la modélisation est significativement non nulle, c'est-à-dire si on peut accepter le modèle. C'est pour cela qu'il faut utiliser le test de Fisher (de l'analyse de la variance) appliqué au modèle, et ensuite regarder le coefficient de corrélation linéaire. Il ne faut pas accorder une confiance aveugle à ces tests, qui peuvent être mis en défaut notamment pour de petits échantillons. On doit donc systématiquement réaliser une analyse des résidus, ce qui peut souvent se réduire à des tracés diagnostics que fournit la fonction plot.lm() du package stats. C'est ce qui explique que R fournit 6 tracés (dont 4 seulement par défaut) pour plot.lm(modele) qui est équivalent à plot(lm(modele)).
Pour obtenir les 6 tracés, il faut utiliser le paramètre which :
# lecture des données
km <- lit.dar("km.dar")
# tracé des 6 graphiques de diagnostics pour le modèle
ml <- lm(essence ~ distance,data=km)
for (idg in (1:6)) {
plot(ml,which=idg)
} # fin pour idg
# tracés et stockage des tracés dans des fichiers PNG
par(ask=FALSE)
for (idg in (1:6)) {
fgr <- paste("kmdiagno_",idg,".png",sep="")
gr(fgr)
plot(ml,which=idg)
dev.off()
cat("fichier ",fgr," généré.\n")
} # fin pour idg
Les graphiques obtenus se nomment tracés de diagnostic du modèle et viennent analyser les résidus, les points-leviers, les outliers... Ici par exemple, les trois premiers graphiques montrent que les trajets 3, 6 et 10 semblent ne pas bien être en accord avec le modèle.
Avec la fonction predict() appliquée à un data frame avec les mêmes noms de variables, on peut utiliser le modèle linéaire pour prédire de nouvelles valeurs :
# lecture des données
km <- lit.dar("km.dar")
# régression linéaire
ml <- lm(essence ~ distance,data=km)
# prédictions
cats("valeurs prédites")
newx <- c(100,250)
# surtout pas
# newy <- predict(ml,newx)
# car cela produit l'erreur
# Erreur dans eval(predvars, data, env) :
# argument numérique 'envir' n'ayant une longueur unitaire
# on construit un nouveau data frame avec le même nom pour x
newxdf <- data.frame(distance=newx)
newy <- predict(ml,newxdf)
print(rbind(newx,newy))
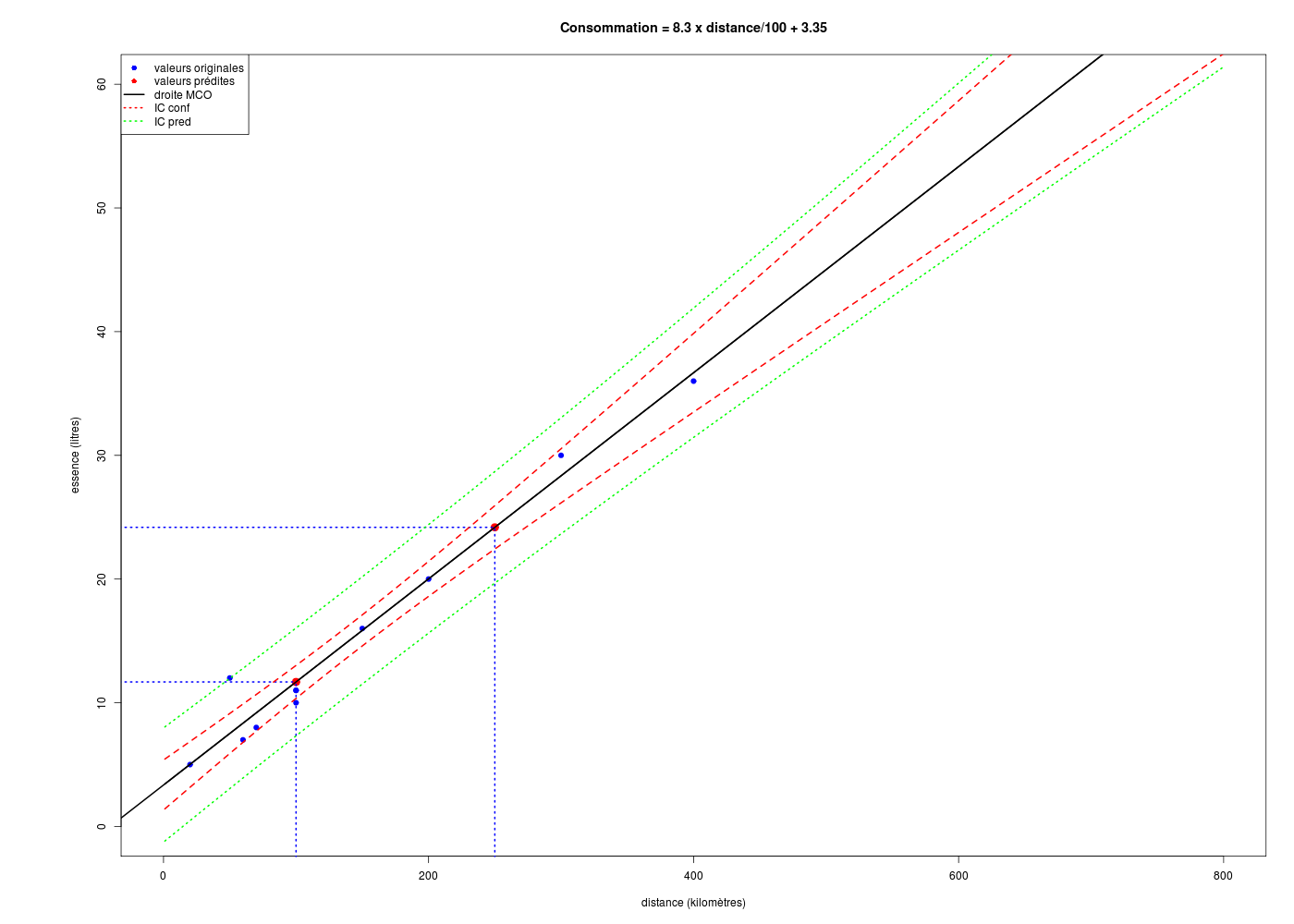
# tracé avec ajout des points prédits et des intervalles de confiance
co <- round(coef(ml),3)
idx <- order(km$distance)
formule <- paste("Consommation = ", 100*co[2]," x distance/100 + ",co[1],sep="")
gr("kmpreds.png")
par(omi=c(0,1,0,0)) # pour avoir plus place à gauche de l'axe
with( km,
plot(essence[idx]~distance[idx],type="p",
pch=19,col="blue",xlim=c(0,800),ylim=c(0,60),
xlab="distance (kilomètres)",ylab="essence (litres)",main=formule
) # fin de plot
) # fin de with
abline(ml,lwd=2,col="black") # droite de régression (moindres carrés ordinaires)
# points pour lesquels on veut une prédiction
points(cbind(newx,newy),cex=1.5,col="red",pch=19)
lines(rep(newx[1],2),c(-10,newy[1]),lty=3,col="blue",lwd=2)
lines(rep(newx[2],2),c(-10,newy[2]),lty=3,col="blue",lwd=2)
lines(c(-50,newx[1]),rep(newy[1],2),lty=3,col="blue",lwd=2)
lines(c(-50,newx[2]),rep(newy[2],2),lty=3,col="blue",lwd=2)
# tracé des intervalles de confiance
grillex <- data.frame(distance=1:800)
icConf <- predict(ml,new=grillex,interval="confidence",level=0.95)
icPred <- predict(ml,new=grillex,interval="prediction",level=0.95)
matlines(grillex,cbind(icConf,icPred[,-1]),lty=c(1,2,2,3,3),col=c("black","red","red","green","green"),lwd=2)
# un légende, c'est utile
legend(
x="topleft",
legend=c("valeurs originales","valeurs prédites","droite MCO","IC conf","IC pred"),
col=c("blue","red","black","red","green"),
pch=c(19,19,NA,NA,NA),
lty=c(0,0,1,3,3),
lwd=c(0,0,2,2,2)
) # fin de legend
dev.off()
valeurs prédites
================
1 2
newx 100.00000 250.00000
newy 11.68237 24.18035
Il y a bien sûr ici une relation de causalité, la cause étant la distance et l'effet étant la consommation, ce que l'on peut résumer par plus on roule, plus on consomme.
3. Régression linéaire multiple
Effectuez une première RLM (Régression Linéaire Multiple de LN_NID en fonction de ALT, PENTE, HAUT et DIAM, puis une seconde en utilisant seulement ALT, PENTE et HAUT, puis une troisième avec ALT, PENTE et DIAM dans le dossier CHENILLES.
Y a-t-il une différence au niveau du signe des coefficients calculés ?
Quel est le meilleur de ces trois modèles ? Faut-il distinguer le meilleur modèle prédictif du meilleur modèle explicatif ?
Que peut-on en conclure sur l'influence de la colinéarité des variables dans une RLM ?
Comment demander à R de calculer le meilleur modèle pour LN_NID à partir des quatre variables ALT, PENTE, HAUT et DIAM ?
Voici le code R pour réaliser les régressions demandées :
attach(chen)
# régression 1
cats("Régression numéro 1 ")
m1 <- lm( LN_NID ~ ALT + PENTE + HAUT + DIAM )
print(summary(m1))
fit1 <- m1$fitted.values
# régression 2
cats("Régression numéro 2 ")
m2 <- lm( LN_NID ~ ALT + PENTE + HAUT )
print(summary(m2))
fit2 <- m2$fitted.values
# régression 3
cats("Régression numéro 3 ")
m3 <- lm( LN_NID ~ ALT + PENTE + DIAM )
print(summary(m3))
fit3 <- m3$fitted.values
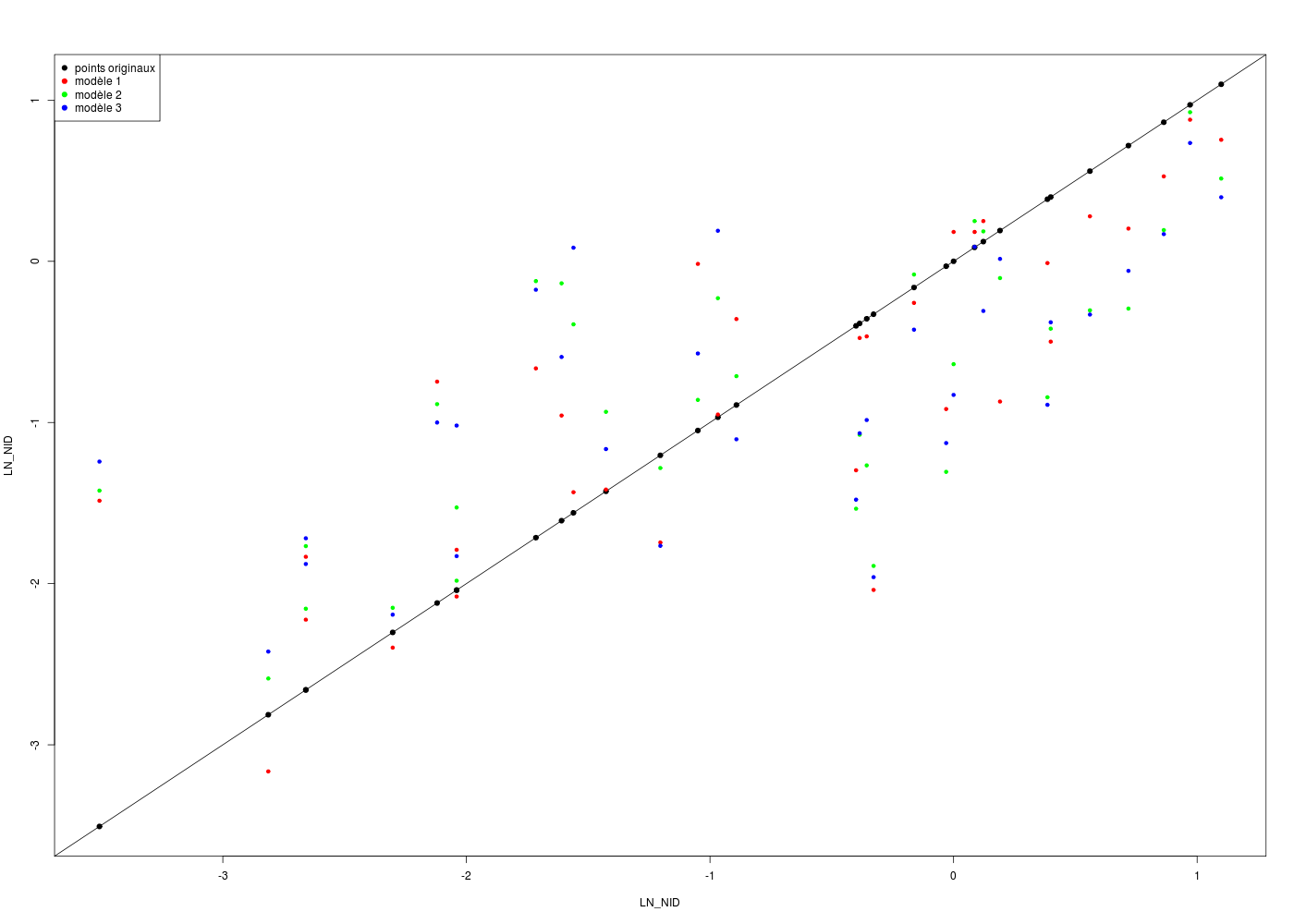
# tracés
gr("chen3modeles.png")
plot(LN_NID,LN_NID,pch=19,col="black")
abline(a=0,b=1)
points(LN_NID,fit1,pch=19,col="red",cex=0.7)
points(LN_NID,fit2,pch=19,col="green",cex=0.7)
points(LN_NID,fit3,pch=19,col="blue",cex=0.7)
legend(
x="topleft",
legend=c("points originaux","modèle 1","modèle 2","modèle 3"),
col=c("black","red","green","blue"),
pch=19
) # fin de legend
dev.off()
detach(chen)
Et les résultats correspondants :
Régression numéro 1
=====================
Call:
lm(formula = LN_NID ~ ALT + PENTE + HAUT + DIAM)
Residuals:
Min 1Q Median 3Q Max
-2.02087 -0.25012 0.09002 0.35179 1.71056
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.732147 1.488585 5.194 1.63e-05 ***
ALT -0.003924 0.001148 -3.419 0.001946 **
PENTE -0.057343 0.019388 -2.958 0.006236 **
HAUT -1.356138 0.319834 -4.240 0.000220 ***
DIAM 0.283059 0.076260 3.712 0.000905 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.7906 on 28 degrees of freedom
Multiple R-squared: 0.6471, Adjusted R-squared: 0.5967
F-statistic: 12.83 on 4 and 28 DF, p-value: 4.677e-06
Régression numéro 2
=====================
Call:
lm(formula = LN_NID ~ ALT + PENTE + HAUT)
Residuals:
Min 1Q Median 3Q Max
-2.0837 -0.5037 -0.0635 0.6903 1.5616
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.448568 1.784311 4.174 0.000249 ***
ALT -0.003986 0.001377 -2.894 0.007153 **
PENTE -0.058997 0.023264 -2.536 0.016860 *
HAUT -0.293479 0.171126 -1.715 0.097016 .
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.949 on 29 degrees of freedom
Multiple R-squared: 0.4734, Adjusted R-squared: 0.419
F-statistic: 8.691 on 3 and 29 DF, p-value: 0.0002869
Régression numéro 3
=====================
Call:
lm(formula = LN_NID ~ ALT + PENTE + DIAM)
Residuals:
Min 1Q Median 3Q Max
-2.2638 -0.7811 0.2125 0.7013 1.6313
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.237019 1.868584 3.873 0.000564 ***
ALT -0.004659 0.001428 -3.262 0.002834 **
PENTE -0.062853 0.024358 -2.580 0.015197 *
DIAM -0.006389 0.042806 -0.149 0.882384
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.9955 on 29 degrees of freedom
Multiple R-squared: 0.4205, Adjusted R-squared: 0.3605
F-statistic: 7.014 on 3 and 29 DF, p-value: 0.001093
Si on compare les modèles 1 et 3, on remarque le coefficient de DIAM est positif avec le modèle 1 (valeur 0.283) mais négatif avec le modèle 3 (valeur -0.006). Compte-tenu de la corrélation entre les varables (détaillée ci-dessous), le coefficient devrait être négatif. C'est sans doute la colinéarité entre HAUT et DIAM (r=0.905) qui cause cette "instabilité" de coefficient.
Le meilleur modèle prédictif de ces trois modèles est le premier, parce que son R2 ajusté est le plus élevé (0.5967 vs 0.4190 et 0.3605).
Malheureusement, ce modèle 1 est sans doute incorrect, à cause du signe de DIAM.
Le meilleur modèle explicatif est certainement le modèle 2.
L'étude de la corrélation entre les variables, y compris la "cible" LN_NID et la régression en fonction de chaque variable séparément peut s'obtenir par :
# données
chen <- lit.dar("chenilles.dar")
# on retire NIDS (variable 11)
chen <- chen[,-11]
# régression de LN_NIDS en fonction chaque variable séparément
nbvar <- 1:(ncol(chen) - 1)
for (idv in nbvar) {
lavar <- names(chen)[idv]
cats(paste("Régression en fonction de",lavar,"seulement"))
fo <- paste("LN_NID ~",lavar)
ml <- lm( as.formula(fo),data=chen)
print(summary(ml))
} # fin pour idv
# matrice des corrélations
mdc(chen)
## tracés de LN_NIDS en fonction chaque variable séparément
# avec la variable pairs() originale
gr("chenpairs1.png")
pairs(chen)
dev.off()
# avec notre fonction pairsi()
gr("chenpairs2.png")
pairsi(chen,opt=2)
dev.off()
Régression en fonction de ALT seulement
=======================================
Call:
lm(formula = as.formula(fo), data = chen)
Residuals:
Min 1Q Median 3Q Max
-2.72074 -0.68616 0.00178 0.94230 1.74964
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5.958414 1.936589 3.077 0.00435 **
ALT -0.005148 0.001465 -3.513 0.00138 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.07 on 31 degrees of freedom
Multiple R-squared: 0.2847, Adjusted R-squared: 0.2617
F-statistic: 12.34 on 1 and 31 DF, p-value: 0.001384
Régression en fonction de PENTE seulement
=========================================
Call:
lm(formula = as.formula(fo), data = chen)
Residuals:
Min 1Q Median 3Q Max
-2.2142 -0.9769 0.2790 0.9433 1.5437
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.31175 0.82689 1.586 0.1228
PENTE -0.07320 0.02765 -2.648 0.0126 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.142 on 31 degrees of freedom
Multiple R-squared: 0.1844, Adjusted R-squared: 0.1581
F-statistic: 7.01 on 1 and 31 DF, p-value: 0.01263
Régression en fonction de PINS seulement
========================================
Call:
lm(formula = as.formula(fo), data = chen)
Residuals:
Min 1Q Median 3Q Max
-2.3184 -0.7781 0.2604 0.8380 1.8454
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.03901 0.29711 -0.131 0.89639
PINS -0.06760 0.02006 -3.370 0.00203 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.082 on 31 degrees of freedom
Multiple R-squared: 0.2681, Adjusted R-squared: 0.2445
F-statistic: 11.36 on 1 and 31 DF, p-value: 0.002027
Régression en fonction de HAUT seulement
========================================
Call:
lm(formula = as.formula(fo), data = chen)
Residuals:
Min 1Q Median 3Q Max
-2.3125 -1.1291 0.2460 0.9391 1.8610
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.4513 0.8882 1.634 0.1124
HAUT -0.5087 0.1944 -2.616 0.0136 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.145 on 31 degrees of freedom
Multiple R-squared: 0.1809, Adjusted R-squared: 0.1545
F-statistic: 6.845 on 1 and 31 DF, p-value: 0.01361
Régression en fonction de DIAM seulement
========================================
Call:
lm(formula = as.formula(fo), data = chen)
Residuals:
Min 1Q Median 3Q Max
-2.5451 -0.9392 0.2989 0.8394 1.7781
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.07346 0.80584 0.091 0.928
DIAM -0.05814 0.05091 -1.142 0.262
Residual standard error: 1.239 on 31 degrees of freedom
Multiple R-squared: 0.04038, Adjusted R-squared: 0.00942
F-statistic: 1.304 on 1 and 31 DF, p-value: 0.2622
Régression en fonction de DENS seulement
========================================
Call:
lm(formula = as.formula(fo), data = chen)
Residuals:
Min 1Q Median 3Q Max
-2.2265 -0.8000 0.2660 0.8289 1.8401
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.8286 0.5095 1.626 0.11400
DENS -0.9168 0.2647 -3.464 0.00158 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.074 on 31 degrees of freedom
Multiple R-squared: 0.2791, Adjusted R-squared: 0.2558
F-statistic: 12 on 1 and 31 DF, p-value: 0.001577
Régression en fonction de ORIEN seulement
=========================================
Call:
lm(formula = as.formula(fo), data = chen)
Residuals:
Min 1Q Median 3Q Max
-2.3924 -0.8565 0.1141 0.9578 1.9767
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.719 1.939 0.887 0.382
ORIEN -1.528 1.163 -1.314 0.199
Residual standard error: 1.231 on 31 degrees of freedom
Multiple R-squared: 0.05275, Adjusted R-squared: 0.0222
F-statistic: 1.726 on 1 and 31 DF, p-value: 0.1985
Régression en fonction de HAUTDOM seulement
===========================================
Call:
lm(formula = as.formula(fo), data = chen)
Residuals:
Min 1Q Median 3Q Max
-1.9251 -0.8830 0.4163 0.8720 1.5343
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.34730 0.63046 2.137 0.04060 *
HAUTDOM -0.28657 0.07994 -3.585 0.00114 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.063 on 31 degrees of freedom
Multiple R-squared: 0.2931, Adjusted R-squared: 0.2703
F-statistic: 12.85 on 1 and 31 DF, p-value: 0.00114
Régression en fonction de STRAT seulement
=========================================
Call:
lm(formula = as.formula(fo), data = chen)
Residuals:
Min 1Q Median 3Q Max
-2.0833 -0.8512 0.2844 0.9167 1.5247
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.7737 0.6537 2.713 0.010780 *
STRAT -1.3054 0.3175 -4.111 0.000268 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.018 on 31 degrees of freedom
Multiple R-squared: 0.3528, Adjusted R-squared: 0.3319
F-statistic: 16.9 on 1 and 31 DF, p-value: 0.0002681
Régression en fonction de MELAN seulement
=========================================
Call:
lm(formula = as.formula(fo), data = chen)
Residuals:
Min 1Q Median 3Q Max
-2.6174 -0.8257 0.4276 0.9753 1.9877
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.2787 1.5406 -0.181 0.858
MELAN -0.3052 0.8706 -0.351 0.728
Residual standard error: 1.262 on 31 degrees of freedom
Multiple R-squared: 0.003949, Adjusted R-squared: -0.02818
F-statistic: 0.1229 on 1 and 31 DF, p-value: 0.7283
Matrice des corrélations au sens de Pearson pour 33 lignes et 11 colonnes
ALT PENTE PINS HAUT DIAM DENS ORIEN HAUTDOM STRAT MELAN LN_NID
ALT 1.000
PENTE 0.121 1.000
PINS 0.538 0.322 1.000
HAUT 0.321 0.137 0.414 1.000
DIAM 0.284 0.113 0.295 0.905 1.000
DENS 0.515 0.301 0.980 0.439 0.306 1.000
ORIEN 0.268 -0.152 0.128 0.058 -0.079 0.151 1.000
HAUTDOM 0.360 0.262 0.759 0.772 0.596 0.810 0.060 1.000
STRAT 0.364 0.326 0.877 0.460 0.267 0.909 0.063 0.854 1.000
MELAN -0.100 0.129 0.206 -0.045 -0.025 0.130 0.138 0.054 0.175 1.000
LN_NID -0.534 -0.429 -0.518 -0.425 -0.201 -0.528 -0.230 -0.541 -0.594 -0.063 1.000
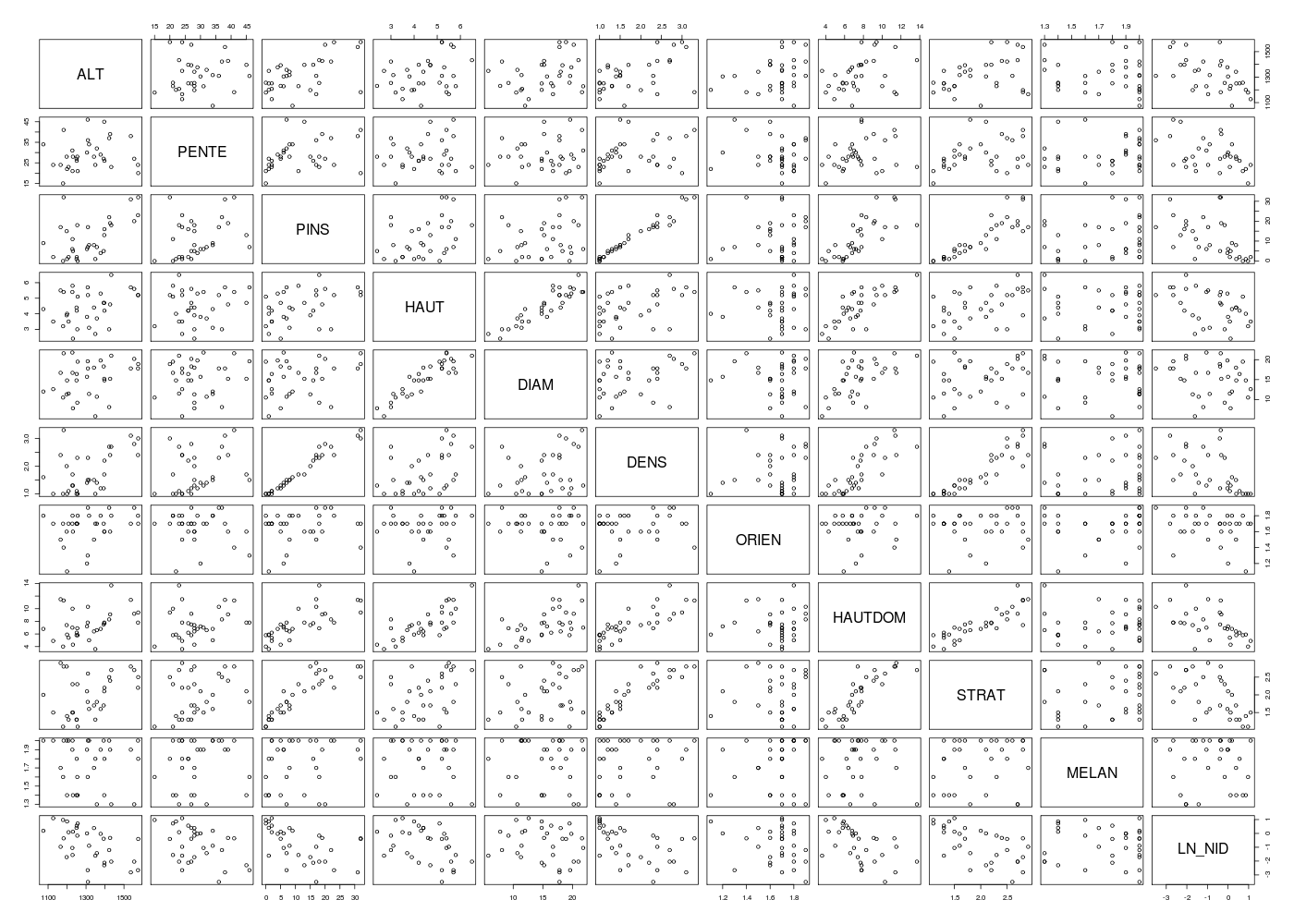 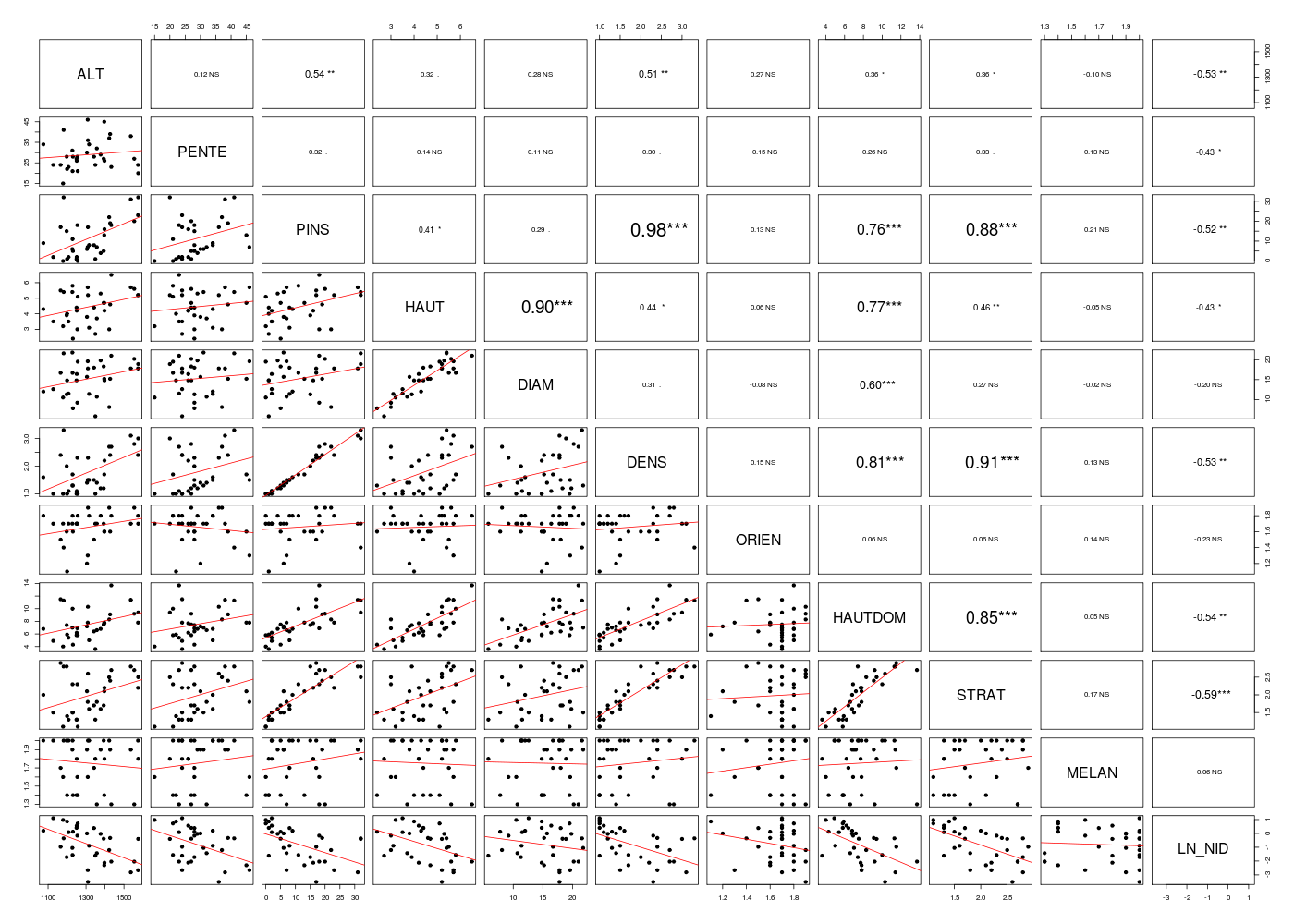
Le dernier graphique montre une tendance négative pour la liaison entre DIAM et LN_NID, d'où notre remarque sur le modèle 1.
La fonction step() permet de déterminer le meilleur modèle par sélection ascendante et descendante de variables :
# lecture des données
che <- lit.dar("chenilles.dar.txt")
# on se restreint aux variables indiquées
chen4v <- che[,c("ALT","PENTE","HAUT","DIAM","LN_NID")]
# modèle minimal
lmMin <- lm(LN_NID~1,data=chen4v)
# modèle maxnimal
lmMax <- lm(LN_NID~.,data=chen4v)
# sélection forward du meilleur modèle
cats("sélection ascendante")
step(lmMin,scope=list(upper=lmMax),trace=1,direction="forward")
# sélection backward du meilleur modèle
cats("sélection descendante")
step(lmMax,scope=list(lower=lmMin),trace=1,direction="backward")
# remarque : sélection sur l'ensemble des variables
catss("sélection globale")
lmMinG <- lm(LN_NID~1,data=che)
lmMaxG <- lm(LN_NID~.,data=che)
cats("sélection ascendante globale")
step(lmMinG,scope=list(upper=lmMaxG),trace=1,direction="forward")
cats("sélection descendante globale")
step(lmMaxG,scope=list(lower=lmMinG),trace=1,direction="backward")
cats("sélection descendante et ascendante")
step(lmMinG,scope=list(upper=lmMaxG),trace=1,direction="both")
# et bien sur sans la variable NIDS
catss("sélection globale sans NIDS")
cheSN <- che[,-11]
lmMinG <- lm(LN_NID~1,data=cheSN)
lmMaxG <- lm(LN_NID~.,data=cheSN)
cats("sélection ascendante globale sans NIDS")
step(lmMinG,scope=list(upper=lmMaxG),trace=1,direction="forward")
cats("sélection descendante globale sans NIDS")
step(lmMaxG,scope=list(lower=lmMinG),trace=1,direction="backward")
cats("sélection descendante et ascendante sans NIDS")
step(lmMinG,scope=list(upper=lmMaxG),trace=1,direction="both")
sélection ascendante
====================
Start: AIC=15.44
LN_NID ~ 1
Df Sum of Sq RSS AIC
+ ALT 1 14.1222 35.474 6.3856
+ PENTE 1 9.1464 40.450 10.7172
+ HAUT 1 8.9707 40.625 10.8602
<none> 49.596 15.4443
+ DIAM 1 2.0025 47.594 16.0843
Step: AIC=6.39
LN_NID ~ ALT
Df Sum of Sq RSS AIC
+ PENTE 1 6.7095 28.764 1.4668
+ HAUT 1 3.5668 31.907 4.8886
<none> 35.474 6.3856
+ DIAM 1 0.1322 35.342 8.2623
Step: AIC=1.47
LN_NID ~ ALT + PENTE
Df Sum of Sq RSS AIC
+ HAUT 1 2.64866 26.116 0.2790
<none> 28.764 1.4668
+ DIAM 1 0.02208 28.742 3.4414
Step: AIC=0.28
LN_NID ~ ALT + PENTE + HAUT
Df Sum of Sq RSS AIC
+ DIAM 1 8.6123 17.503 -10.926
<none> 26.116 0.279
Step: AIC=-10.93
LN_NID ~ ALT + PENTE + HAUT + DIAM
Call:
lm(formula = LN_NID ~ ALT + PENTE + HAUT + DIAM, data = chen4v)
Coefficients:
(Intercept) ALT PENTE HAUT DIAM
7.732147 -0.003924 -0.057343 -1.356138 0.283059
sélection descendante
=====================
Start: AIC=-10.93
LN_NID ~ ALT + PENTE + HAUT + DIAM
Df Sum of Sq RSS AIC
<none> 17.503 -10.9257
- PENTE 1 5.4683 22.972 -3.9540
- ALT 1 7.3067 24.810 -1.4135
- DIAM 1 8.6123 26.116 0.2790
- HAUT 1 11.2389 28.742 3.4414
Call:
lm(formula = LN_NID ~ ALT + PENTE + HAUT + DIAM, data = chen4v)
Coefficients:
(Intercept) ALT PENTE HAUT DIAM
7.732147 -0.003924 -0.057343 -1.356138 0.283059
+ ================= +
+ +
+ sélection globale +
+ +
+ ================= +
sélection ascendante globale
============================
Start: AIC=15.44
LN_NID ~ 1
Df Sum of Sq RSS AIC
+ NIDS 1 38.072 11.524 -30.7186
+ STRAT 1 17.499 32.097 3.0848
+ HAUTDOM 1 14.536 35.060 5.9986
+ ALT 1 14.122 35.474 6.3856
+ DENS 1 13.841 35.755 6.6459
+ PINS 1 13.297 36.299 7.1445
+ PENTE 1 9.146 40.450 10.7172
+ HAUT 1 8.971 40.625 10.8602
<none> 49.596 15.4443
+ ORIEN 1 2.616 46.980 15.6559
+ DIAM 1 2.002 47.594 16.0843
+ MELAN 1 0.196 49.400 17.3138
Step: AIC=-30.72
LN_NID ~ NIDS
Df Sum of Sq RSS AIC
+ HAUT 1 0.70995 10.814 -30.817
<none> 11.524 -30.719
+ ALT 1 0.32905 11.195 -29.675
+ HAUTDOM 1 0.24374 11.280 -29.424
+ DIAM 1 0.19999 11.324 -29.296
+ STRAT 1 0.11318 11.411 -29.044
+ MELAN 1 0.10510 11.419 -29.021
+ ORIEN 1 0.10125 11.423 -29.010
+ DENS 1 0.06037 11.464 -28.892
+ PENTE 1 0.05779 11.466 -28.884
+ PINS 1 0.04093 11.483 -28.836
Step: AIC=-30.82
LN_NID ~ NIDS + HAUT
Df Sum of Sq RSS AIC
+ DIAM 1 0.69885 10.115 -31.021
<none> 10.814 -30.817
+ ALT 1 0.19360 10.620 -29.413
+ ORIEN 1 0.11195 10.702 -29.160
+ PENTE 1 0.07140 10.743 -29.035
+ MELAN 1 0.05941 10.755 -28.999
+ HAUTDOM 1 0.03580 10.778 -28.926
+ STRAT 1 0.00474 10.809 -28.831
+ PINS 1 0.00097 10.813 -28.820
+ DENS 1 0.00018 10.814 -28.817
Step: AIC=-31.02
LN_NID ~ NIDS + HAUT + DIAM
Df Sum of Sq RSS AIC
<none> 10.1152 -31.021
+ ALT 1 0.41371 9.7015 -30.400
+ PENTE 1 0.19232 9.9229 -29.655
+ HAUTDOM 1 0.15231 9.9629 -29.522
+ MELAN 1 0.02261 10.0926 -29.095
+ ORIEN 1 0.01665 10.0985 -29.076
+ STRAT 1 0.01133 10.1038 -29.058
+ DENS 1 0.00230 10.1129 -29.029
+ PINS 1 0.00113 10.1140 -29.025
Call:
lm(formula = LN_NID ~ NIDS + HAUT + DIAM, data = che)
Coefficients:
(Intercept) NIDS HAUT DIAM
-0.86290 1.19199 -0.50992 0.08869
sélection descendante globale
=============================
Start: AIC=-19.42
LN_NID ~ ALT + PENTE + PINS + HAUT + DIAM + DENS + ORIEN + HAUTDOM +
STRAT + MELAN + NIDS
Df Sum of Sq RSS AIC
- ORIEN 1 0.0001 8.8527 -21.4210
- MELAN 1 0.0155 8.8681 -21.3637
- DENS 1 0.0518 8.9043 -21.2292
- PINS 1 0.1159 8.9684 -20.9923
- STRAT 1 0.1525 9.0050 -20.8580
- HAUTDOM 1 0.3073 9.1598 -20.2954
- PENTE 1 0.4532 9.3057 -19.7741
<none> 8.8525 -19.4216
- ALT 1 0.5751 9.4276 -19.3445
- DIAM 1 0.9891 9.8417 -17.9262
- HAUT 1 1.4373 10.2898 -16.4566
- NIDS 1 6.2773 15.1299 -3.7346
Step: AIC=-21.42
LN_NID ~ ALT + PENTE + PINS + HAUT + DIAM + DENS + HAUTDOM +
STRAT + MELAN + NIDS
Df Sum of Sq RSS AIC
- MELAN 1 0.0168 8.8695 -23.3583
- DENS 1 0.0589 8.9116 -23.2021
- PINS 1 0.1264 8.9791 -22.9531
- STRAT 1 0.1661 9.0188 -22.8076
- HAUTDOM 1 0.3145 9.1672 -22.2690
- PENTE 1 0.4696 9.3223 -21.7154
<none> 8.8527 -21.4210
- ALT 1 0.5960 9.4487 -21.2707
- DIAM 1 1.1896 10.0423 -19.2602
- HAUT 1 1.6953 10.5480 -17.6389
- NIDS 1 6.3155 15.1682 -5.6511
Step: AIC=-23.36
LN_NID ~ ALT + PENTE + PINS + HAUT + DIAM + DENS + HAUTDOM +
STRAT + NIDS
Df Sum of Sq RSS AIC
- DENS 1 0.0436 8.9131 -25.1965
- PINS 1 0.1106 8.9801 -24.9492
- STRAT 1 0.1788 9.0483 -24.6996
- HAUTDOM 1 0.3103 9.1798 -24.2236
- PENTE 1 0.4568 9.3264 -23.7009
<none> 8.8695 -23.3583
- ALT 1 0.5895 9.4591 -23.2346
- DIAM 1 1.1807 10.0502 -21.2342
- HAUT 1 1.6933 10.5629 -19.5924
- NIDS 1 6.6786 15.5481 -6.8348
Step: AIC=-25.2
LN_NID ~ ALT + PENTE + PINS + HAUT + DIAM + HAUTDOM + STRAT +
NIDS
Df Sum of Sq RSS AIC
- PINS 1 0.1018 9.0149 -26.8217
- STRAT 1 0.2258 9.1389 -26.3708
- HAUTDOM 1 0.2672 9.1803 -26.2219
- PENTE 1 0.4322 9.3453 -25.6338
<none> 8.9131 -25.1965
- ALT 1 0.6467 9.5598 -24.8849
- DIAM 1 1.1528 10.0659 -23.1828
- HAUT 1 1.6602 10.5733 -21.5597
- NIDS 1 6.6380 15.5511 -8.8285
Step: AIC=-26.82
LN_NID ~ ALT + PENTE + HAUT + DIAM + HAUTDOM + STRAT + NIDS
Df Sum of Sq RSS AIC
- STRAT 1 0.1252 9.1401 -28.3665
- HAUTDOM 1 0.3019 9.3168 -27.7348
- PENTE 1 0.3788 9.3937 -27.4634
- ALT 1 0.5590 9.5739 -26.8364
<none> 9.0149 -26.8217
- DIAM 1 1.2879 10.3028 -24.4150
- HAUT 1 1.8765 10.8914 -22.5815
- NIDS 1 7.3061 16.3210 -9.2338
Step: AIC=-28.37
LN_NID ~ ALT + PENTE + HAUT + DIAM + HAUTDOM + NIDS
Df Sum of Sq RSS AIC
- HAUTDOM 1 0.2170 9.3572 -29.5921
- PENTE 1 0.4028 9.5430 -28.9432
<none> 9.1401 -28.3665
- ALT 1 0.5900 9.7301 -28.3023
- DIAM 1 1.3283 10.4685 -25.8886
- HAUT 1 1.7550 10.8951 -24.5703
- NIDS 1 8.3282 17.4683 -8.9919
Step: AIC=-29.59
LN_NID ~ ALT + PENTE + HAUT + DIAM + NIDS
Df Sum of Sq RSS AIC
- PENTE 1 0.3443 9.7015 -30.400
- ALT 1 0.5657 9.9229 -29.655
<none> 9.3572 -29.592
- DIAM 1 1.1472 10.5044 -27.776
- HAUT 1 1.6400 10.9972 -26.263
- NIDS 1 8.1462 17.5034 -10.926
Step: AIC=-30.4
LN_NID ~ ALT + HAUT + DIAM + NIDS
Df Sum of Sq RSS AIC
- ALT 1 0.4137 10.1152 -31.021
<none> 9.7015 -30.400
- DIAM 1 0.9190 10.6204 -29.413
- HAUT 1 1.3915 11.0929 -27.977
- NIDS 1 13.2703 22.9717 -3.954
Step: AIC=-31.02
LN_NID ~ HAUT + DIAM + NIDS
Df Sum of Sq RSS AIC
<none> 10.115 -31.0215
- DIAM 1 0.6989 10.814 -30.8169
- HAUT 1 1.2088 11.324 -29.2963
- NIDS 1 21.2832 31.398 4.3582
Call:
lm(formula = LN_NID ~ HAUT + DIAM + NIDS, data = che)
Coefficients:
(Intercept) HAUT DIAM NIDS
-0.86290 -0.50992 0.08869 1.19199
sélection descendante et ascendante
===================================
Start: AIC=15.44
LN_NID ~ 1
Df Sum of Sq RSS AIC
+ NIDS 1 38.072 11.524 -30.7186
+ STRAT 1 17.499 32.097 3.0848
+ HAUTDOM 1 14.536 35.060 5.9986
+ ALT 1 14.122 35.474 6.3856
+ DENS 1 13.841 35.755 6.6459
+ PINS 1 13.297 36.299 7.1445
+ PENTE 1 9.146 40.450 10.7172
+ HAUT 1 8.971 40.625 10.8602
<none> 49.596 15.4443
+ ORIEN 1 2.616 46.980 15.6559
+ DIAM 1 2.002 47.594 16.0843
+ MELAN 1 0.196 49.400 17.3138
Step: AIC=-30.72
LN_NID ~ NIDS
Df Sum of Sq RSS AIC
+ HAUT 1 0.710 10.814 -30.817
<none> 11.524 -30.719
+ ALT 1 0.329 11.195 -29.675
+ HAUTDOM 1 0.244 11.280 -29.424
+ DIAM 1 0.200 11.324 -29.296
+ STRAT 1 0.113 11.411 -29.044
+ MELAN 1 0.105 11.419 -29.021
+ ORIEN 1 0.101 11.423 -29.010
+ DENS 1 0.060 11.464 -28.892
+ PENTE 1 0.058 11.466 -28.884
+ PINS 1 0.041 11.483 -28.836
- NIDS 1 38.072 49.596 15.444
Step: AIC=-30.82
LN_NID ~ NIDS + HAUT
Df Sum of Sq RSS AIC
+ DIAM 1 0.6989 10.115 -31.021
<none> 10.814 -30.817
- HAUT 1 0.7099 11.524 -30.719
+ ALT 1 0.1936 10.620 -29.413
+ ORIEN 1 0.1119 10.702 -29.160
+ PENTE 1 0.0714 10.743 -29.035
+ MELAN 1 0.0594 10.755 -28.999
+ HAUTDOM 1 0.0358 10.778 -28.926
+ STRAT 1 0.0047 10.809 -28.831
+ PINS 1 0.0010 10.813 -28.820
+ DENS 1 0.0002 10.814 -28.817
- NIDS 1 29.8113 40.625 10.860
Step: AIC=-31.02
LN_NID ~ NIDS + HAUT + DIAM
Df Sum of Sq RSS AIC
<none> 10.1152 -31.0215
- DIAM 1 0.6989 10.8140 -30.8169
+ ALT 1 0.4137 9.7015 -30.3996
+ PENTE 1 0.1923 9.9229 -29.6550
+ HAUTDOM 1 0.1523 9.9629 -29.5222
- HAUT 1 1.2088 11.3240 -29.2963
+ MELAN 1 0.0226 10.0926 -29.0954
+ ORIEN 1 0.0167 10.0985 -29.0759
+ STRAT 1 0.0113 10.1038 -29.0585
+ DENS 1 0.0023 10.1129 -29.0291
+ PINS 1 0.0011 10.1140 -29.0252
- NIDS 1 21.2832 31.3984 4.3582
Call:
lm(formula = LN_NID ~ NIDS + HAUT + DIAM, data = che)
Coefficients:
(Intercept) NIDS HAUT DIAM
-0.86290 1.19199 -0.50992 0.08869
+ =========================== +
+ +
+ sélection globale sans NIDS +
+ +
+ =========================== +
sélection ascendante globale sans NIDS
======================================
Start: AIC=15.44
LN_NID ~ 1
Df Sum of Sq RSS AIC
+ STRAT 1 17.4987 32.097 3.0848
+ HAUTDOM 1 14.5357 35.060 5.9986
+ ALT 1 14.1222 35.474 6.3856
+ DENS 1 13.8412 35.755 6.6459
+ PINS 1 13.2969 36.299 7.1445
+ PENTE 1 9.1464 40.450 10.7172
+ HAUT 1 8.9707 40.625 10.8602
<none> 49.596 15.4443
+ ORIEN 1 2.6164 46.980 15.6559
+ DIAM 1 2.0025 47.594 16.0843
+ MELAN 1 0.1958 49.400 17.3138
Step: AIC=3.08
LN_NID ~ STRAT
Df Sum of Sq RSS AIC
+ ALT 1 5.7642 26.333 -1.4474
+ PENTE 1 3.0899 29.008 1.7446
<none> 32.097 3.0848
+ ORIEN 1 1.8378 30.260 3.1390
+ HAUT 1 1.4585 30.639 3.5502
+ HAUTDOM 1 0.2153 31.882 4.8627
+ DIAM 1 0.0945 32.003 4.9875
+ MELAN 1 0.0853 32.012 4.9971
+ DENS 1 0.0368 32.061 5.0470
+ PINS 1 0.0020 32.095 5.0828
Step: AIC=-1.45
LN_NID ~ STRAT + ALT
Df Sum of Sq RSS AIC
+ PENTE 1 3.07012 23.263 -3.5382
+ DENS 1 2.27340 24.060 -2.4269
+ PINS 1 1.94158 24.392 -1.9749
<none> 26.333 -1.4474
+ HAUT 1 0.60003 25.733 -0.2080
+ ORIEN 1 0.55986 25.773 -0.1565
+ HAUTDOM 1 0.04815 26.285 0.4922
+ DIAM 1 0.03828 26.295 0.5046
+ MELAN 1 0.01903 26.314 0.5288
Step: AIC=-3.54
LN_NID ~ STRAT + ALT + PENTE
Df Sum of Sq RSS AIC
+ PINS 1 2.42797 20.835 -5.1757
+ DENS 1 2.34020 20.923 -5.0370
<none> 23.263 -3.5382
+ ORIEN 1 1.21501 22.048 -3.3084
+ HAUT 1 0.64494 22.618 -2.4660
+ HAUTDOM 1 0.07706 23.186 -1.6477
+ DIAM 1 0.06082 23.202 -1.6246
+ MELAN 1 0.00000 23.263 -1.5382
Step: AIC=-5.18
LN_NID ~ STRAT + ALT + PENTE + PINS
Df Sum of Sq RSS AIC
+ ORIEN 1 1.38056 19.454 -5.4381
<none> 20.835 -5.1757
+ HAUT 1 0.47688 20.358 -3.9398
+ MELAN 1 0.13013 20.705 -3.3824
+ DENS 1 0.10288 20.732 -3.3390
+ HAUTDOM 1 0.07171 20.763 -3.2895
+ DIAM 1 0.03910 20.796 -3.2377
Step: AIC=-5.44
LN_NID ~ STRAT + ALT + PENTE + PINS + ORIEN
Df Sum of Sq RSS AIC
<none> 19.454 -5.4381
+ HAUT 1 0.50574 18.949 -4.3073
+ DENS 1 0.28304 19.172 -3.9218
+ HAUTDOM 1 0.08666 19.368 -3.5855
+ MELAN 1 0.01632 19.438 -3.4658
+ DIAM 1 0.00004 19.454 -3.4382
Call:
lm(formula = LN_NID ~ STRAT + ALT + PENTE + PINS + ORIEN, data = cheSN)
Coefficients:
(Intercept) STRAT ALT PENTE PINS ORIEN
11.107720 -1.745234 -0.004373 -0.054446 0.071498 -1.175855
sélection descendante globale sans NIDS
=======================================
Start: AIC=-3.73
LN_NID ~ ALT + PENTE + PINS + HAUT + DIAM + DENS + ORIEN + HAUTDOM +
STRAT + MELAN
Df Sum of Sq RSS AIC
- DENS 1 0.0357 15.166 -5.6569
- ORIEN 1 0.0383 15.168 -5.6511
- MELAN 1 0.2389 15.369 -5.2177
- PINS 1 0.3208 15.451 -5.0422
- HAUTDOM 1 0.4023 15.532 -4.8685
<none> 15.130 -3.7346
- STRAT 1 1.5190 16.649 -2.5774
- DIAM 1 3.3869 18.517 0.9317
- HAUT 1 3.6205 18.750 1.3453
- PENTE 1 4.1551 19.285 2.2730
- ALT 1 5.5717 20.702 4.6122
Step: AIC=-5.66
LN_NID ~ ALT + PENTE + PINS + HAUT + DIAM + ORIEN + HAUTDOM +
STRAT + MELAN
Df Sum of Sq RSS AIC
- ORIEN 1 0.0871 15.253 -7.4679
- MELAN 1 0.2063 15.372 -7.2110
- HAUTDOM 1 0.3742 15.540 -6.8525
<none> 15.166 -5.6569
- PINS 1 0.9909 16.156 -5.5683
- STRAT 1 1.8513 17.017 -3.8560
- DIAM 1 3.5100 18.676 -0.7866
- HAUT 1 4.0339 19.199 0.1263
- PENTE 1 4.1218 19.287 0.2771
- ALT 1 5.5373 20.703 2.6142
Step: AIC=-7.47
LN_NID ~ ALT + PENTE + PINS + HAUT + DIAM + HAUTDOM + STRAT +
MELAN
Df Sum of Sq RSS AIC
- MELAN 1 0.2984 15.551 -8.8285
- HAUTDOM 1 0.3782 15.631 -8.6597
- PINS 1 0.9455 16.198 -7.4832
<none> 15.253 -7.4679
- STRAT 1 1.7752 17.028 -5.8346
- PENTE 1 4.0447 19.297 -1.7058
- DIAM 1 4.7047 19.957 -0.5960
- HAUT 1 4.9416 20.194 -0.2066
- ALT 1 6.3926 21.645 2.0831
Step: AIC=-8.83
LN_NID ~ ALT + PENTE + PINS + HAUT + DIAM + HAUTDOM + STRAT
Df Sum of Sq RSS AIC
- HAUTDOM 1 0.4992 16.050 -9.7858
- PINS 1 0.7699 16.321 -9.2338
<none> 15.551 -8.8285
- STRAT 1 1.9116 17.463 -7.0027
- PENTE 1 4.1556 19.707 -3.0132
- DIAM 1 4.5302 20.081 -2.3918
- HAUT 1 4.8757 20.427 -1.8288
- ALT 1 6.1082 21.659 0.1045
Step: AIC=-9.79
LN_NID ~ ALT + PENTE + PINS + HAUT + DIAM + STRAT
Df Sum of Sq RSS AIC
- PINS 1 0.9272 16.977 -9.9325
<none> 16.050 -9.7858
- STRAT 1 1.4451 17.495 -8.9408
- PENTE 1 4.2645 20.315 -4.0102
- DIAM 1 4.3079 20.358 -3.9398
- HAUT 1 4.7457 20.796 -3.2377
- ALT 1 6.6711 22.721 -0.3156
Step: AIC=-9.93
LN_NID ~ ALT + PENTE + HAUT + DIAM + STRAT
Df Sum of Sq RSS AIC
- STRAT 1 0.5259 17.503 -10.9257
<none> 16.977 -9.9325
- PENTE 1 4.0243 21.002 -4.9127
- DIAM 1 5.6406 22.618 -2.4660
- ALT 1 5.8582 22.836 -2.1500
- HAUT 1 6.2248 23.202 -1.6246
Step: AIC=-10.93
LN_NID ~ ALT + PENTE + HAUT + DIAM
Df Sum of Sq RSS AIC
<none> 17.503 -10.9257
- PENTE 1 5.4683 22.972 -3.9540
- ALT 1 7.3067 24.810 -1.4135
- DIAM 1 8.6123 26.116 0.2790
- HAUT 1 11.2389 28.742 3.4414
Call:
lm(formula = LN_NID ~ ALT + PENTE + HAUT + DIAM, data = cheSN)
Coefficients:
(Intercept) ALT PENTE HAUT DIAM
7.732147 -0.003924 -0.057343 -1.356138 0.283059
sélection descendante et ascendante sans NIDS
=============================================
Start: AIC=15.44
LN_NID ~ 1
Df Sum of Sq RSS AIC
+ STRAT 1 17.4987 32.097 3.0848
+ HAUTDOM 1 14.5357 35.060 5.9986
+ ALT 1 14.1222 35.474 6.3856
+ DENS 1 13.8412 35.755 6.6459
+ PINS 1 13.2969 36.299 7.1445
+ PENTE 1 9.1464 40.450 10.7172
+ HAUT 1 8.9707 40.625 10.8602
<none> 49.596 15.4443
+ ORIEN 1 2.6164 46.980 15.6559
+ DIAM 1 2.0025 47.594 16.0843
+ MELAN 1 0.1958 49.400 17.3138
Step: AIC=3.08
LN_NID ~ STRAT
Df Sum of Sq RSS AIC
+ ALT 1 5.7642 26.333 -1.4474
+ PENTE 1 3.0899 29.008 1.7446
<none> 32.097 3.0848
+ ORIEN 1 1.8378 30.260 3.1390
+ HAUT 1 1.4585 30.639 3.5502
+ HAUTDOM 1 0.2153 31.882 4.8627
+ DIAM 1 0.0945 32.003 4.9875
+ MELAN 1 0.0853 32.012 4.9971
+ DENS 1 0.0368 32.061 5.0470
+ PINS 1 0.0020 32.095 5.0828
- STRAT 1 17.4987 49.596 15.4443
Step: AIC=-1.45
LN_NID ~ STRAT + ALT
Df Sum of Sq RSS AIC
+ PENTE 1 3.0701 23.263 -3.5382
+ DENS 1 2.2734 24.060 -2.4269
+ PINS 1 1.9416 24.392 -1.9749
<none> 26.333 -1.4474
+ HAUT 1 0.6000 25.733 -0.2080
+ ORIEN 1 0.5599 25.773 -0.1565
+ HAUTDOM 1 0.0482 26.285 0.4922
+ DIAM 1 0.0383 26.295 0.5046
+ MELAN 1 0.0190 26.314 0.5288
- ALT 1 5.7642 32.097 3.0848
- STRAT 1 9.1407 35.474 6.3856
Step: AIC=-3.54
LN_NID ~ STRAT + ALT + PENTE
Df Sum of Sq RSS AIC
+ PINS 1 2.4280 20.835 -5.1757
+ DENS 1 2.3402 20.923 -5.0370
<none> 23.263 -3.5382
+ ORIEN 1 1.2150 22.048 -3.3084
+ HAUT 1 0.6449 22.618 -2.4660
+ HAUTDOM 1 0.0771 23.186 -1.6477
+ DIAM 1 0.0608 23.202 -1.6246
+ MELAN 1 0.0000 23.263 -1.5382
- PENTE 1 3.0701 26.333 -1.4474
- STRAT 1 5.5013 28.764 1.4668
- ALT 1 5.7445 29.008 1.7446
Step: AIC=-5.18
LN_NID ~ STRAT + ALT + PENTE + PINS
Df Sum of Sq RSS AIC
+ ORIEN 1 1.3806 19.454 -5.4381
<none> 20.835 -5.1757
+ HAUT 1 0.4769 20.358 -3.9398
- PINS 1 2.4280 23.263 -3.5382
+ MELAN 1 0.1301 20.705 -3.3824
+ DENS 1 0.1029 20.732 -3.3390
+ HAUTDOM 1 0.0717 20.763 -3.2895
+ DIAM 1 0.0391 20.796 -3.2377
- PENTE 1 3.5565 24.392 -1.9749
- STRAT 1 6.5118 27.347 1.7992
- ALT 1 8.1381 28.973 3.7054
Step: AIC=-5.44
LN_NID ~ STRAT + ALT + PENTE + PINS + ORIEN
Df Sum of Sq RSS AIC
<none> 19.454 -5.4381
- ORIEN 1 1.3806 20.835 -5.1757
+ HAUT 1 0.5057 18.949 -4.3073
+ DENS 1 0.2830 19.172 -3.9218
+ HAUTDOM 1 0.0867 19.368 -3.5855
+ MELAN 1 0.0163 19.438 -3.4658
+ DIAM 1 0.0000 19.454 -3.4382
- PINS 1 2.5935 22.048 -3.3084
- PENTE 1 4.3177 23.772 -0.8237
- ALT 1 6.4077 25.862 1.9570
- STRAT 1 6.6742 26.129 2.2954
Call:
lm(formula = LN_NID ~ STRAT + ALT + PENTE + PINS + ORIEN, data = cheSN)
Coefficients:
(Intercept) STRAT ALT PENTE PINS ORIEN
11.107720 -1.745234 -0.004373 -0.054446 0.071498 -1.175855
4. Régression logistique simple
Réaliser la régression de la variable binaire de cardiopathie coronarienne (CHD69) à l'aide de la seule variable AGE dans le dossier WCGS.
Quel est le rapport de côte pour une augmentation de l'age d'un an ? Et pour 10 ans ?
Quelle est la probabilité d'avoir l'évènement pour une personne de 55 ans ?
Données : wcgs.dar.
Commençons par regarder les variables CHD69 et AGE séparément puis conjointement.
# lecture des données
WCGS <- lit.dar("wcgs.dar")
age <- WCGS$AGE
# recodage de chd
chd <- factor(WCGS$CHD69,labels=c("Non","Oui"))
chd69 <- ifelse(chd=="Non",0,1)
# statistiques élémentaires
decritQT("AGE dans WCGS",age,"ans",TRUE,"wcgs_age.png")
decritQL("CHD dans WCGS",chd69,c("Non","Oui"),TRUE,"wcgs_chd.png")
decritQTparFacteur(
titreQT="AGE dans WCGS",
nomVarQT=age,
unite="ans",
titreQL="CHD",
nomVarQL=chd69,
labels=c("Non","Oui"),
graphique=TRUE,
fichier_image="wcgs1.png"
) # fin de decritQTparFacteur
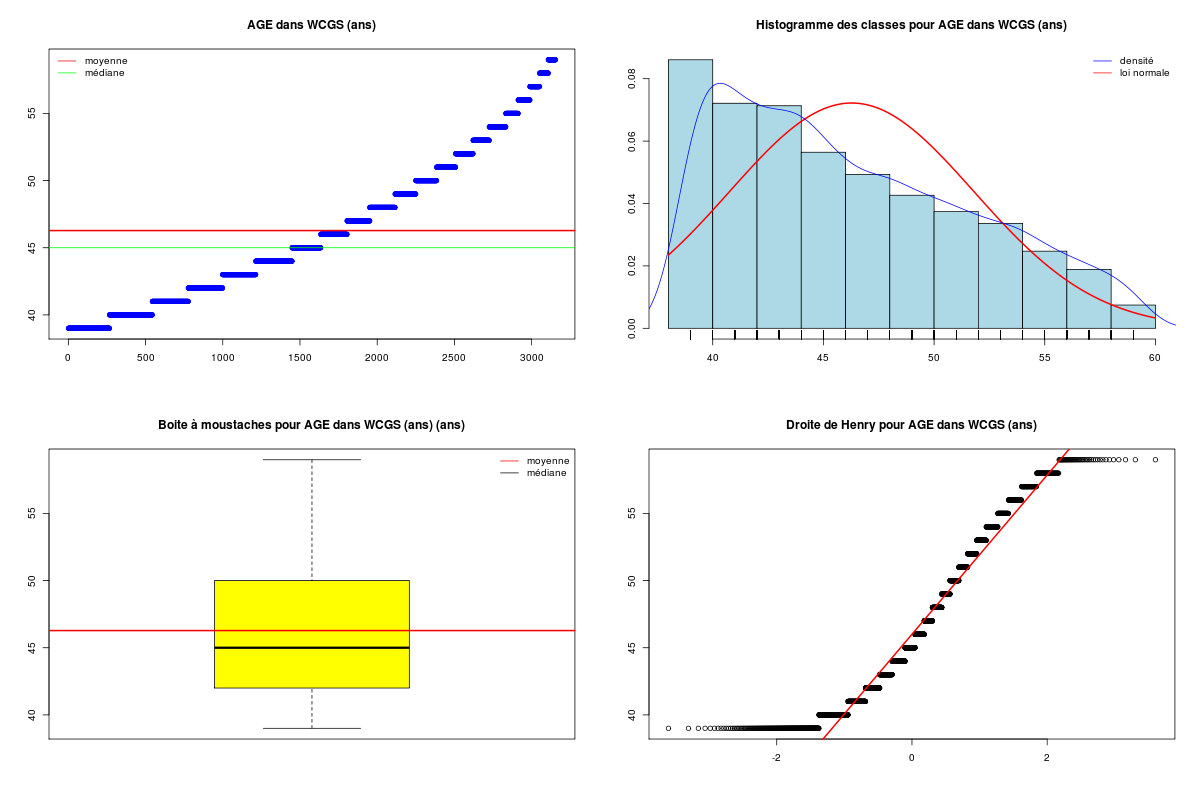
DESCRIPTION STATISTIQUE DE LA VARIABLE AGE dans WCGS
Taille 3154 individus
Moyenne 46.2787 ans
Ecart-type 5.5240 ans
Coef. de variation 12 %
1er Quartile 42.0000 ans
Mediane 45.0000 ans
3eme Quartile 50.0000 ans
iqr absolu 8.0000 ans
iqr relatif 18.0000 %
Minimum 39 ans
Maximum 59 ans
Tracé tige et feuilles
The decimal point is at the |
39 | 0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000+136
40 | 0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000+147
41 | 0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000+103
42 | 0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000+92
43 | 0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000+85
44 | 0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000+105
45 | 0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000+56
46 | 0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000+40
47 | 0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000+17
48 | 0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000+34
49 | 0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000+4
50 | 0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000+5
51 | 0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
52 | 00000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
53 | 000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
54 | 00000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
55 | 00000000000000000000000000000000000000000000000000000000000000000000000000000000
56 | 0000000000000000000000000000000000000000000000000000000000000000000000000000
57 | 000000000000000000000000000000000000000000000000000000000000000
58 | 00000000000000000000000000000000000000000000000000000000
59 | 00000000000000000000000000000000000000000000000
vous pouvez utiliser wcgs_age.png
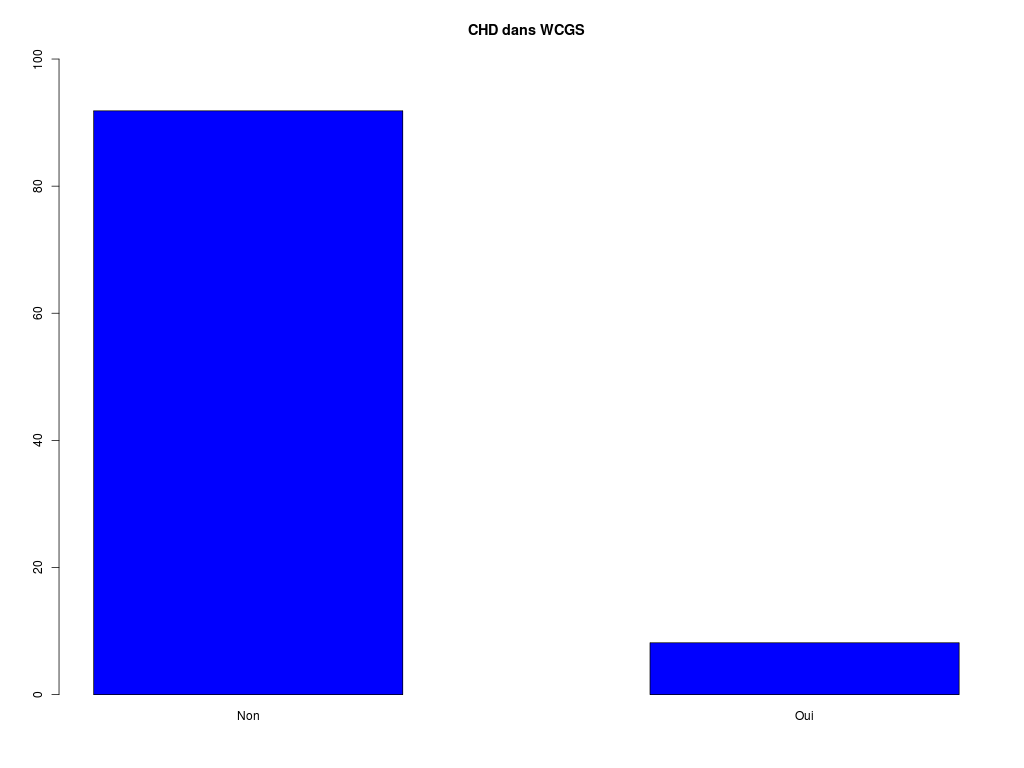
TRI A PLAT DE : CHD dans WCGS (ordre des modalités)
Non Oui Total
Effectif 2897 257 3154
Cumul Effectif 2897 3154 3154
Frequence (en %) 92 8 100
Cumul fréquences 92 100 100
VARIABLE : CHD dans WCGS (par fréquence décroissante)
Non Oui Total
Effectif 2897 257 3154
Cumul Effectif 2897 3154 3154
Frequence (en %) 92 8 100
Cumul fréquences 92 100 100
[1] "Non" "Oui"
vous pouvez utiliser wcgs_chd.png
VARIABLE QT AGE dans WCGS ,unit=ans
VARIABLE QL CHD labels : Non Oui
N Moy Unite Ect Cdv Q1 Med Q3 EIQ Min
Global 3154 46.279 ans 5.523 12 42.000 45.000 50.000 8.000 39.000
Non 2897 46.082 ans 5.456 12 41.000 45.000 50.000 9.000 39.000
Oui 257 48.490 ans 5.790 12 44.000 49.000 53.000 9.000 39.000
Max
Global 59.000
Non 59.000
Oui 59.000
Analysis of Variance Table
Response: nomVarQT
Df Sum Sq Mean Sq F value Pr(>F)
ql 1 1369 1368.52 45.48 1.827e-11 ***
Residuals 3152 94846 30.09
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Kruskal-Wallis rank sum test
data: nomVarQT by ql
Kruskal-Wallis chi-squared = 40.8787, df = 1, p-value = 1.62e-10
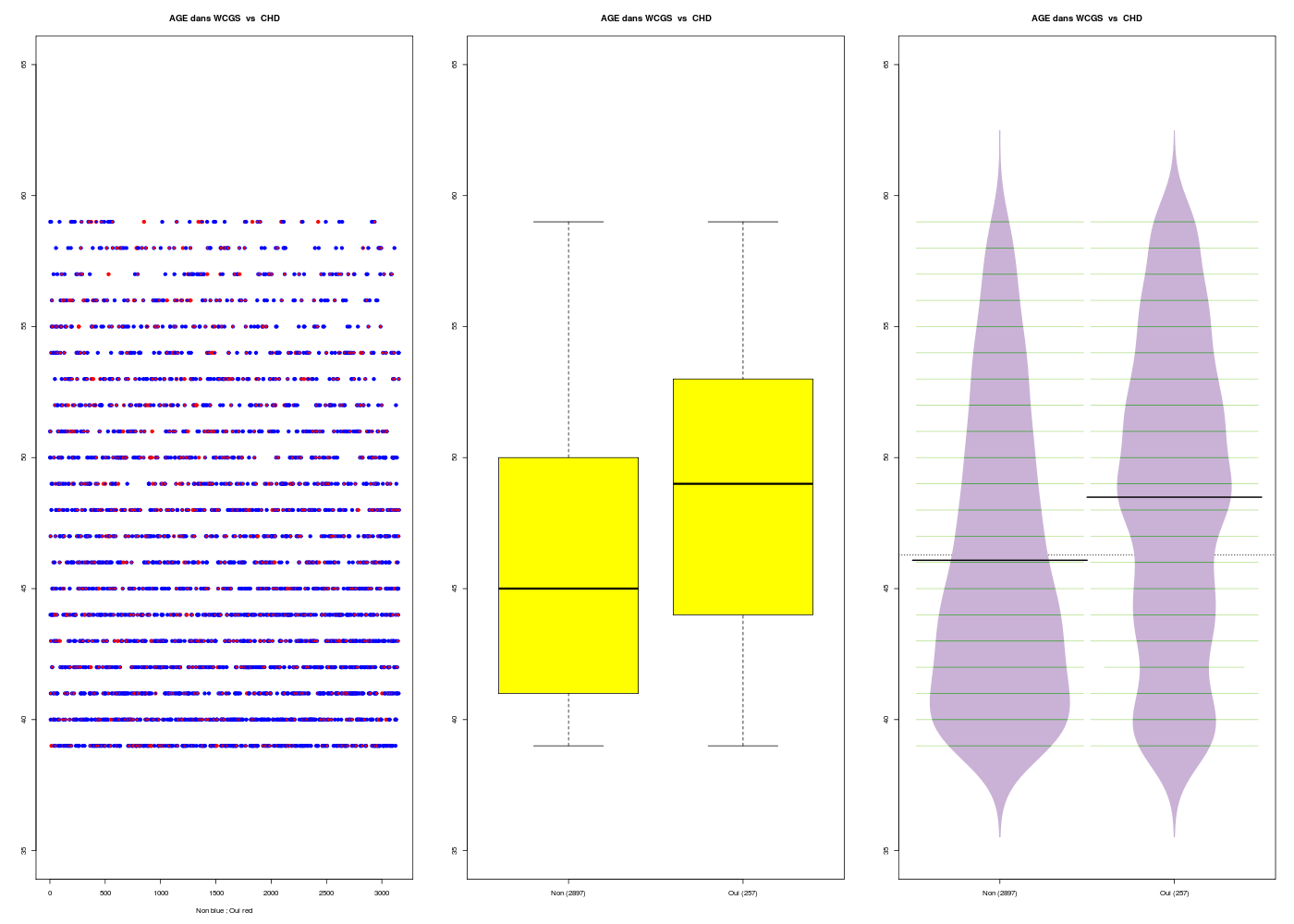
On peut en conclure que pour les données présentées, l'AGE est assez homogène (cdv=12 %), peu étendu et non normal, et que la CHD est assez peu présente (8 %), avec une différence significative selon l'age (p<<0,0001).
Réalisons maintenant la régression logistique de la variable CHD69 (binaire) à l'aide de la seule variable AGE (continue) à l'aide de la fonction glm et dont les résultats peuvent être consultés via la fonction summary.glm. Comme il est d'usage de rapporter la log-vraisemblance du modèle, les intervalles de confiance des coefficients, le rapport de vraisemblance (LR) et le R2, nous utilisons, en plus des fonctions confint et logLik du package élémentaire stats les fonctions confint.glm et lrm des packages MASS et Design qui fournissent directement ces valeurs. Remarque : la fonction classique anova fournit aussi le LR (qu'elle nomme Deviance).
# lecture des données
WCGS <- lit.dar("wcgs.dar")
age <- WCGS$AGE
chd <- factor(WCGS$CHD69,labels=c("Non","Oui"))
# régression logistique
rlb <- glm( formula = chd ~ age, family = binomial() )
summary.glm( rlb )
anova( rlb )
# il manque la log-vraisemblance et les intervalles de confiance
logLik( rlb )
library(MASS)
confint( rlb )
# l'intervalle calculé par Stata dans le livre de Vittinghoff correspond
# à l'intervalle sous hypothèse de normalité asymptotique
confint.default( rlb )
library(Design)
lrm( rlb )
> rlb <- glm( formula = chd ~ age, family = binomial() )
> summary.glm( rlb )
Call:
glm(formula = chd ~ age, family = binomial())
Deviance Residuals:
Min 1Q Median 3Q Max
-0.6208 -0.4545 -0.3668 -0.3292 2.4835
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -5.93952 0.54932 -10.813 < 2e-16 ***
age 0.07442 0.01130 6.585 4.56e-11 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 1781.2 on 3153 degrees of freedom
Residual deviance: 1738.4 on 3152 degrees of freedom
AIC: 1742.4
Number of Fisher Scoring iterations: 5
> anova( rlb )
Analysis of Deviance Table
Model: binomial, link: logit
Response: chd
Terms added sequentially (first to last)
Df Deviance Resid. Df Resid. Dev
NULL 3153 1781.2
age 1 42.888 3152 1738.4
> logLik( rlb )
'log Lik.' -869.178 (df=2)
> library(MASS)
> confint( rlb )
2.5 % 97.5 %
(Intercept) -7.02449218 -4.86960992
age 0.05227351 0.09661197
> confint.default( rlb )
2.5 % 97.5 %
(Intercept) -7.01616019 -4.86287169
age 0.05227038 0.09657473
> library(Design)
> lrm( rlb )
Logistic Regression Model
lrm(formula = rlb)
Frequencies of Responses
Non Oui
2897 257
Obs Max Deriv Model L.R. d.f. P C Dxy Gamma Tau-a R2 Brier
3154 9e-08 42.89 1 0 0.62 0.24 0.252 0.036 0.031 0.074
Coef S.E. Wald Z P
Intercept -5.93952 0.54932 -10.81 0
age 0.07442 0.01130 6.58 0
Le rapport de côte p/(1-p) pour une augmentation de l'age d'un an s'obtient en prenant l'exponentielle du coefficient β1, soit ici exp(0.074*1) qui vaut à peu près 1,077 ; pour 10 ans, c'est exp(0.074*10) soit 2,105.
La probabilité d'avoir un trouble coronarien pour une personne de 55 ans se calcule avec la fonction logistique :
p(55) = exp(-5.940+0.074*55)/(1 + exp(-5.940+0.074*55)) = 0.1335417
5. Régression logistique multiple
Réalisez la régression de la variable de cardiopathie coronarienne (CHD69) à l'aide des 5 variables age, chol, sbp, bmi et smoke dans le dossier WCGS.
Quel est le meilleur modèle ?
Voici, sans explication superflue, le code et les résultats :
# lecture des données
WCGS <- lit.dar("wcgs.dar")
lesv <- c("AGE","CHOL","SBP","BMI","SMOKE")
wcgs <- WCGS[,lesv]
# définition de la matrice des résultats
nbv <- ncol(wcgs)
mdr <- data.frame(matrix(nrow=nbv,ncol=2))
names(mdr) <- c("AUROC","AIC")
row.names(mdr) <- names(wcgs)
# on utilise une boucle pour stocker les AUROC
library(limma) # pour la fonction auROC
for (idv in (1:nbv)) {
rlb <- glm(WCGS$CHD69 ~ wcgs[,idv])
re <- summary(ml)
ypred <- predict(rlb,newdata=wcgs,type="response")
mdr[idv,1] <- auROC(WCGS$CHD69,ypred)
mdr[idv,2] <- rlb$aic
} # fin pour idv
# tri par AUROC décroissante
idx <- order(mdr[,1],decreasing=TRUE)
mdr <- mdr[idx,]
cats("Meilleures régressions logistiques simples pour CHD69 :")
print( round(mdr,2) )
# analyses complémentaires
wcgs <- cbind(WCGS$CHD69,wcgs)
names(wcgs)[1] <- "CHD69"
mdc(wcgs)
gr("wcgs_pairs1.png")
pairsi(wcgs)
dev.off()
Meilleures régressions logistiques simples pour CHD69 :
=======================================================
AUROC AIC
CHOL 0.66 703.84
SBP 0.64 724.07
AGE 0.62 735.22
SMOKE 0.62 757.56
BMI 0.57 768.15
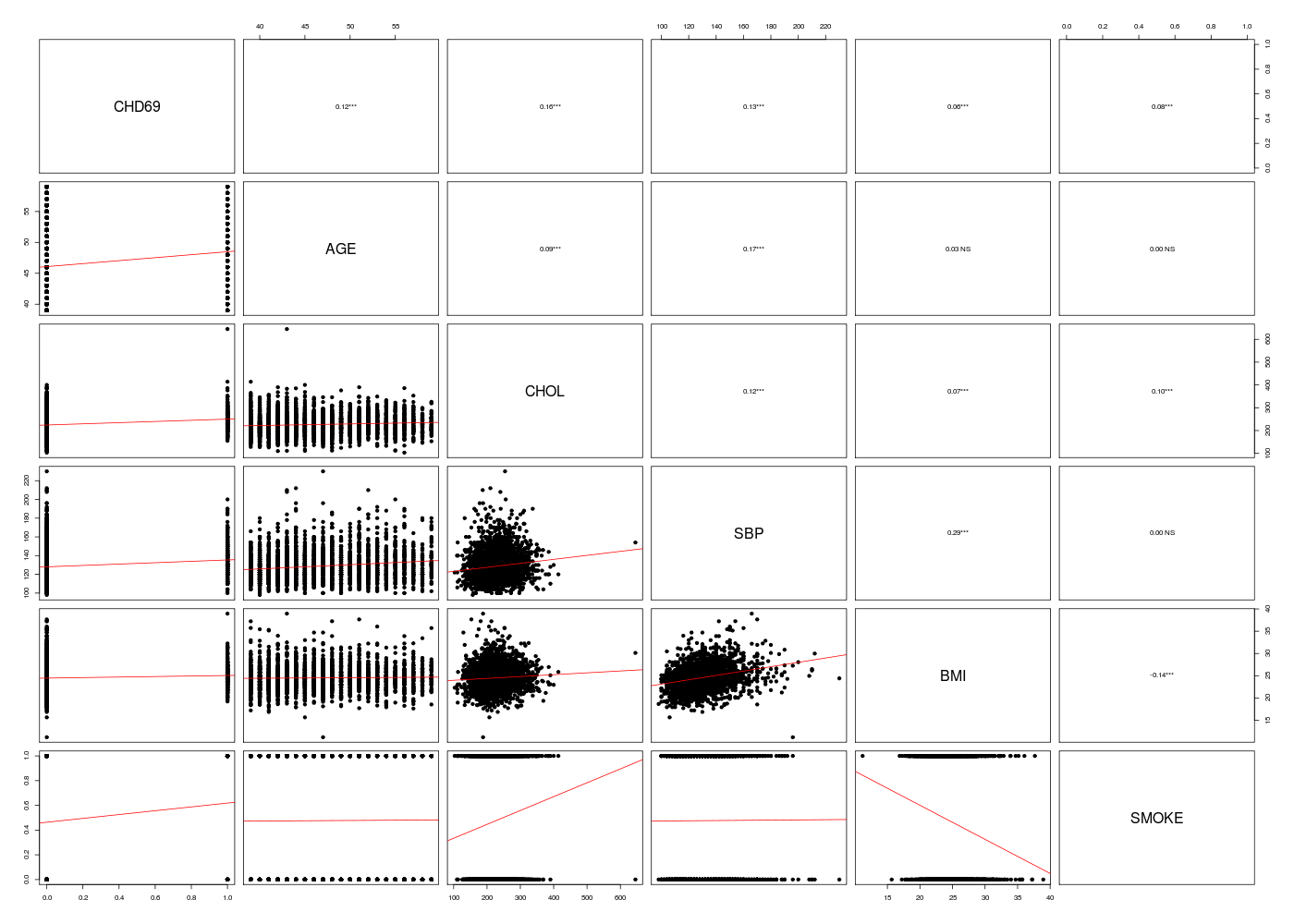
Matrice des corrélations au sens de Pearson pour 3154 lignes et 6 colonnes
CHD69 AGE CHOL SBP BMI SMOKE
CHD69 1.000
AGE 0.119 1.000
CHOL 0.163 0.089 1.000
SBP 0.133 0.166 0.123 1.000
BMI 0.062 0.027 0.071 0.288 1.000
SMOKE 0.085 0.005 0.097 0.003 -0.142 1.000
# lecture des données
WCGS <- lit.dar("wcgs.dar")
lesv1 <- c("AGE","CHOL","SBP","BMI","SMOKE")
lesv2 <- c("ARCUS","DIBPAT")
wcgs <- WCGS[,c(lesv1,lesv2)]
# analyses préliminaires
wcgs <- cbind(WCGS$CHD69,wcgs)
names(wcgs)[1] <- "CHD69"
mdc(wcgs)
gr("wcgs_pairs2.png")
pairsi(wcgs)
dev.off()
# meilleur modèle
rchModeleLogistique(df=wcgs)
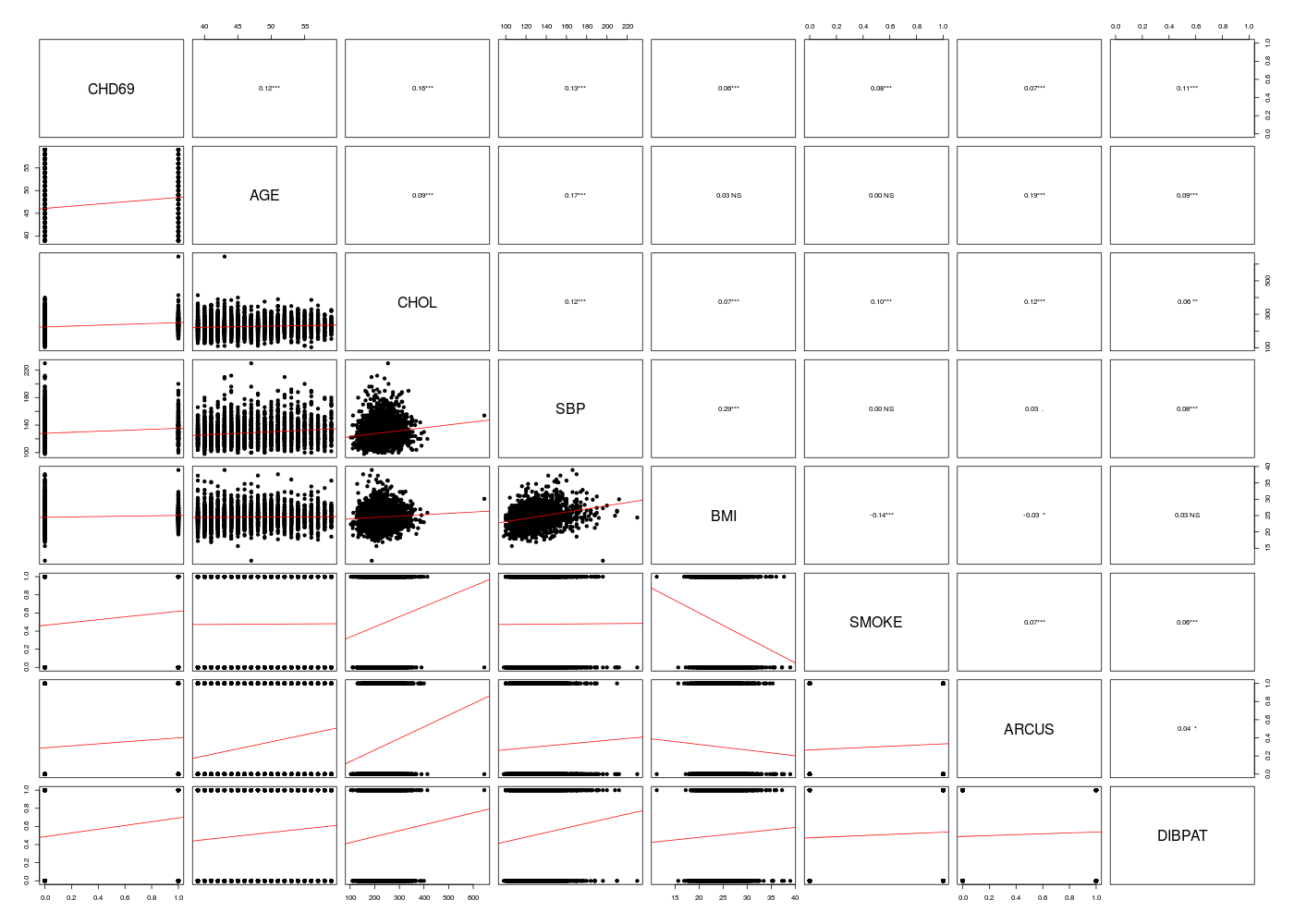
Matrice des corrélations au sens de Pearson pour 3154 lignes et 8 colonnes
CHD69 AGE CHOL SBP BMI SMOKE ARCUS DIBPAT
CHD69 1.000
AGE 0.119 1.000
CHOL 0.163 0.089 1.000
SBP 0.133 0.166 0.123 1.000
BMI 0.062 0.027 0.071 0.288 1.000
SMOKE 0.085 0.005 0.097 0.003 -0.142 1.000
ARCUS 0.066 0.187 0.121 0.034 -0.035 0.073 1.000
DIBPAT 0.112 0.088 0.057 0.077 0.028 0.061 0.044 1.000
RStudioGD
2
AUROC (Intercept) AGE CHOL SBP BMI SMOKE ARCUS DIBPAT AIC
M07V00 0.7503843 -12.274385 0.05718452 0.01038885 0.01821424 0.05948104 0.5986052 0.2190833 0.7021576 1594.445
M07V01 0.6199228 -5.939516 0.07442256 NA NA NA NA NA NA 1742.356
M07V02 0.6624719 -5.359022 NA 0.01244778 NA NA NA NA NA 1706.423
M07V03 0.6313891 -5.926461 NA NA 0.02667129 NA NA NA NA 1736.441
M07V04 0.5661082 -4.508689 NA NA NA 0.08427681 NA NA NA 1773.426
M07V05 0.5775470 -2.763620 NA NA NA NA 0.6298631 NA NA 1762.381
M07V06 0.5551950 -2.599052 NA NA NA NA NA 0.4918141 NA 1762.216
M07V07 0.6027757 -2.934395 NA NA NA NA NA NA 0.8641250 1744.344
M07V-01 0.7368158 -9.906505 NA 0.01033884 0.02161026 0.05373681 0.5563023 0.3531192 0.7427474 1614.084
M07V-02 0.7175185 -10.335688 0.05680841 NA 0.02009451 0.06780513 0.6615986 0.3156082 0.7252050 1643.590
M07V-03 0.7411357 -11.165558 0.06534138 0.01082220 NA 0.09108547 0.6135754 0.1868962 0.7335877 1610.684
M07V-04 0.7455221 -11.070892 0.05591968 0.01057667 0.02058945 NA 0.5478250 0.2089027 0.7086461 1597.388
M07V-05 0.7396840 -11.526847 0.05360428 0.01093851 0.01857986 0.04111321 NA 0.2521781 0.7282620 1610.730
M07V-06 0.7490711 -12.291680 0.06037041 0.01072095 0.01807657 0.05512504 0.6024262 NA 0.6971798 1604.035
M07V-07 0.7345037 -12.313392 0.06118345 0.01052450 0.01937777 0.06209862 0.6284042 0.2202162 NA 1617.149
M07VBS 0.7503843 -12.274385 0.05718452 0.01038885 0.01821424 0.05948104 0.5986052 0.2190833 0.7021576 1594.445
M07VFS 0.7503843 -12.274385 0.05718452 0.01038885 0.01821424 0.05948104 0.5986052 0.2190833 0.7021576 1594.445
M07VMS 0.7503843 -12.274385 0.05718452 0.01038885 0.01821424 0.05948104 0.5986052 0.2190833 0.7021576 1594.445
La fonction step() permet aussi de déterminer le meilleur modèle par sélection ascendante et descendante de variables pour les modèles linéiares généralisésvariables :
# données sans NA
wcgsGLM <- na.omit(wcgs[,(1:6)])
# modèle minimal
glmMin <- glm(as.factor(CHD69)~1,data=wcgsGLM,family=binomial() )
# modèle maxnimal
glmMax <- glm(as.factor(CHD69)~.,data=wcgsGLM,family=binomial() )
# sélection forward du meilleur modèle
cats("sélection ascendante")
step(glmMin,scope=list(upper=glmMax),trace=1,direction="forward")
# sélection backward du meilleur modèle
cats("sélection descendante")
step(glmMax,scope=list(lower=glmMin),trace=1,direction="backward")
sélection ascendante
====================
Start: AIC=1781.2
as.factor(CHD69) ~ 1
Df Deviance AIC
+ CHOL 1 1702.4 1706.4
+ SBP 1 1729.5 1733.5
+ AGE 1 1736.0 1740.0
+ SMOKE 1 1756.2 1760.2
+ BMI 1 1767.2 1771.2
<none> 1779.2 1781.2
Step: AIC=1706.42
as.factor(CHD69) ~ CHOL
Df Deviance AIC
+ SBP 1 1664.1 1670.1
+ AGE 1 1665.8 1671.8
+ SMOKE 1 1686.6 1692.6
+ BMI 1 1693.7 1699.7
<none> 1702.4 1706.4
Step: AIC=1670.08
as.factor(CHD69) ~ CHOL + SBP
Df Deviance AIC
+ AGE 1 1637.8 1645.8
+ SMOKE 1 1647.2 1655.2
<none> 1664.1 1670.1
+ BMI 1 1662.5 1670.5
Step: AIC=1645.8
as.factor(CHD69) ~ CHOL + SBP + AGE
Df Deviance AIC
+ SMOKE 1 1619.3 1629.3
+ BMI 1 1635.6 1645.6
<none> 1637.8 1645.8
Step: AIC=1629.34
as.factor(CHD69) ~ CHOL + SBP + AGE + SMOKE
Df Deviance AIC
+ BMI 1 1614.6 1626.6
<none> 1619.3 1629.3
Step: AIC=1626.61
as.factor(CHD69) ~ CHOL + SBP + AGE + SMOKE + BMI
Call: glm(formula = as.factor(CHD69) ~ CHOL + SBP + AGE + SMOKE + BMI,
family = binomial(), data = wcgsGLM)
Coefficients:
(Intercept) CHOL SBP AGE SMOKE BMI
-12.33630 0.01084 0.01930 0.06436 0.63269 0.05767
Degrees of Freedom: 3141 Total (i.e. Null); 3136 Residual
Null Deviance: 1779
Residual Deviance: 1615 AIC: 1627
sélection descendante
=====================
Start: AIC=1626.61
as.factor(CHD69) ~ AGE + CHOL + SBP + BMI + SMOKE
Df Deviance AIC
<none> 1614.6 1626.6
- BMI 1 1619.3 1629.3
- SMOKE 1 1635.6 1645.6
- SBP 1 1635.7 1645.7
- AGE 1 1643.6 1653.6
- CHOL 1 1668.8 1678.8
Call: glm(formula = as.factor(CHD69) ~ AGE + CHOL + SBP + BMI + SMOKE,
family = binomial(), data = wcgsGLM)
Coefficients:
(Intercept) AGE CHOL SBP BMI SMOKE
-12.33630 0.06436 0.01084 0.01930 0.05767 0.63269
Degrees of Freedom: 3141 Total (i.e. Null); 3136 Residual
Null Deviance: 1779
Residual Deviance: 1615 AIC: 1627
Code-source php de cette page. Retour à la page principale du cours.
|
 Retour à la page principale de
(gH)
Retour à la page principale de
(gH)