1. Vocabulaire usuel des statistiques
Comment traduit-on en anglais et en R les termes classiques de variable, loi, moyenne, médiane, etc. ?
Le tableau suivant, en deux parties, montre les termes anglais de R associés aux termes français via les noms de fonctions en R ainsi que les termes correspondant liés aux graphiques.
| Taille |
length() |
| Moyenne |
mean() |
| Médiane |
median() |
| Variance |
var() |
| Ecart type |
sd() |
| Quantile |
quantile() |
| Minimum |
min() |
| Maximum |
max() |
|
|
| Courbes (lignes) |
plot() |
| Points supplémentaires |
points() |
| Lignes supplémentaires |
abline() |
| Courbes multiples |
pairs() |
| Histogramme de fréquences |
hist() |
| Histogramme d'effectifs |
barplot() |
| Boite à moustaches |
boxplot() |
| Diagramme tige et feuilles |
stem() |
|
2. Fonctions de base pour analyses univariées de variables qualitatives
Comment est implémentée en R la notion de variable qualitative ? Quelles sont les fonctions R associées ?
Quelles précautions faut-il prendre quand on lit avec R un fichier texte avec des colonnes de caractères ?
Analyser la variable Règne taxonomique dans les données lea.dar. On trouvera des informations sur ces données à l'URL lea.htm. Que peut-on en conclure ?
Une variable qualitative est implémentée en R via la fonction factor(). On peut préciser les modalités nommées par R levels et leurs textes nommés par R labels. La fonction principale est table() pour les calculs et barplot() pour les graphiques, mais on peut bien sûr utiliser summary() et plot() qui sont des fonctions génériques.
# un mini-exemple de variable qualitative
dataQl <- c("F","H","F","H","H")
ql <- factor(x=dataQl,levels=c("F","H"),labels=c("femme","homme"))
cat("voici les données :\n")
print(ql)
cat("leur comptage :\n")
print(table(ql)) # on peut aussi utiliser print(summary(ql))
cat("maintenant, deux petits tracés :\n")
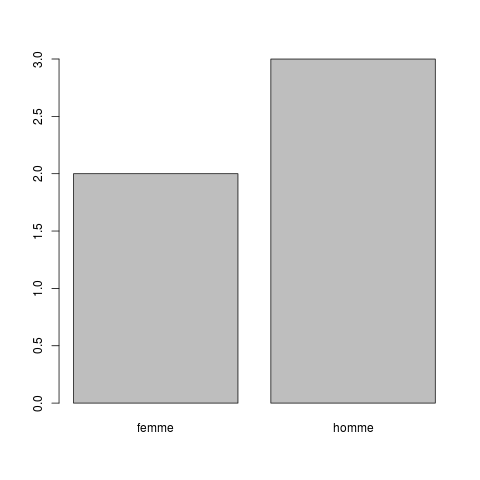
plot(ql)
barplot(table(ql))
voici les données :
[1] femme homme femme homme homme
Levels: femme homme
leur comptage :
ql
femme homme
2 3
et leur résumé :
femme homme
2 3
maintenant, deux petits tracés :
Lorsqu'on lit un fichier texte avec R, toute variable numérique est considérée comme quantitative et toute variable caractère comme qualitative. Voici par exemple ce que donne la lecture de elfQL.data :
# lecture de elfQL.data, la colonne SEXE est écrite en H/F
dataElf <- read.table("elfQL.data",header=TRUE,row.names=1)
print(summary(dataElf))
SEXE AGE PROF ETUD REGI USAG
F:64 Min. :11.00 Min. : 0.000 Min. :0.000 Min. :0.000 Min. :0.0000
H:35 1st Qu.:22.00 1st Qu.: 6.000 1st Qu.:2.000 1st Qu.:1.000 1st Qu.:0.0000
Median :29.00 Median : 8.000 Median :3.000 Median :2.000 Median :0.0000
Mean :35.83 Mean : 7.808 Mean :2.879 Mean :2.525 Mean :0.5051
3rd Qu.:48.50 3rd Qu.:12.000 3rd Qu.:4.000 3rd Qu.:4.000 3rd Qu.:1.0000
Max. :78.00 Max. :16.000 Max. :4.000 Max. :4.000 Max. :3.0000
Si on ne dispose que des codes-numériques pour les qualitatives, il ne faut pas oublier de convertir en facteur, comme pour elf.data car sinon on peut calculer des moyennes de codes :
# lecture de elfQL.data, la colonne SEXE est écrite en 0/1
# on la lit incorrectement en numérique
dataElf <- read.table("elf.data",header=TRUE,row.names=1)
cat("\nrésumés incorrects\n\n")
print(summary(dataElf))
# lecture correcte : on convertit en facteur
cat("\nrésumés corrects\n\n")
dataElf <- read.table("elf.data",header=TRUE,row.names=1)
dataElf$SEXE <- factor(dataElf$SEXE,levels=0:1,labels=c("Homme","Femme"))
print(summary(dataElf))
résumés incorrects
SEXE AGE PROF ETUD REGI USAG
Min. :0.0000 Min. :11.00 Min. : 0.000 Min. :0.000 Min. :0.000 Min. :0.0000
1st Qu.:0.0000 1st Qu.:22.00 1st Qu.: 6.000 1st Qu.:2.000 1st Qu.:1.000 1st Qu.:0.0000
Median :1.0000 Median :29.00 Median : 8.000 Median :3.000 Median :2.000 Median :0.0000
Mean :0.6465 Mean :35.83 Mean : 7.808 Mean :2.879 Mean :2.525 Mean :0.5051
3rd Qu.:1.0000 3rd Qu.:48.50 3rd Qu.:12.000 3rd Qu.:4.000 3rd Qu.:4.000 3rd Qu.:1.0000
Max. :1.0000 Max. :78.00 Max. :16.000 Max. :4.000 Max. :4.000 Max. :3.0000
résumés corrects
SEXE AGE PROF ETUD REGI USAG
Homme:35 Min. :11.00 Min. : 0.000 Min. :0.000 Min. :0.000 Min. :0.0000
Femme:64 1st Qu.:22.00 1st Qu.: 6.000 1st Qu.:2.000 1st Qu.:1.000 1st Qu.:0.0000
Median :29.00 Median : 8.000 Median :3.000 Median :2.000 Median :0.0000
Mean :35.83 Mean : 7.808 Mean :2.879 Mean :2.525 Mean :0.5051
3rd Qu.:48.50 3rd Qu.:12.000 3rd Qu.:4.000 3rd Qu.:4.000 3rd Qu.:1.0000
Max. :78.00 Max. :16.000 Max. :4.000 Max. :4.000 Max. :3.0000
Il peut arriver dans certains cas que l'on veuille conserver la colonne en mode caractère. C'est possible avec l'option as.is=TRUE de la fonction read.table() ou avec l'option stringsAsFactors=FALSE :
# lecture de elfQL.data, la colonne SEXE est écrite en H/F
# on la lit sans la convertir en facteur
dataElf <- read.table("elfQL.data",header=TRUE,row.names=1,as.is=TRUE)
cat("\nrésumés \n\n")
print(summary(dataElf))
résumés
SEXE AGE PROF ETUD REGI USAG
Length:99 Min. :11.00 Min. : 0.000 Min. :0.000 Min. :0.000 Min. :0.0000
Class :character 1st Qu.:22.00 1st Qu.: 6.000 1st Qu.:2.000 1st Qu.:1.000 1st Qu.:0.0000
Mode :character Median :29.00 Median : 8.000 Median :3.000 Median :2.000 Median :0.0000
Mean :35.83 Mean : 7.808 Mean :2.879 Mean :2.525 Mean :0.5051
3rd Qu.:48.50 3rd Qu.:12.000 3rd Qu.:4.000 3rd Qu.:4.000 3rd Qu.:1.0000
Max. :78.00 Max. :16.000 Max. :4.000 Max. :4.000 Max. :3.0000
L'analyse de la variable Règne taxonomique dans les données lea.dar est simple à réaliser avec les fonctions déjà citées :
# lecture des données
url <- "http://www.info.univ-angers.fr/~gh/Datasets/lea.dar"
lea <- read.table(url,header=TRUE,row.names=1)
reign <- lea$reign
# calculs QL
effs <- table(reign)
tria <- round(100*table(reign)/length(reign) )
# affichage
cat("Effectifs absolus\n")
print( effs )
cat("Effectifs relatifs (\"tri à plat\")\n")
print( tria )
# histogramme des fréquences relatives
barplot(tria)
Effectifs absolus
reign
Alveolata Bacteria Euryarchaeota Fungi Metazoa Parabasalidea Viridiplantae
1 38 1 11 23 1 698
Effectifs relatifs ("tri à plat")
reign
Alveolata Bacteria Euryarchaeota Fungi Metazoa Parabasalidea Viridiplantae
0 5 0 1 3 0 90
Avec toutes les fonctions que nous mettons à disposition dans statgh.r, c'est encore plus court à écrire :
# lecture des données
url <- "http://www.info.univ-angers.fr/~gh/Datasets/lea.dar"
lea <- lit.dar(url)
reign <- factor(lea$reign)
# calculs QL et tracé
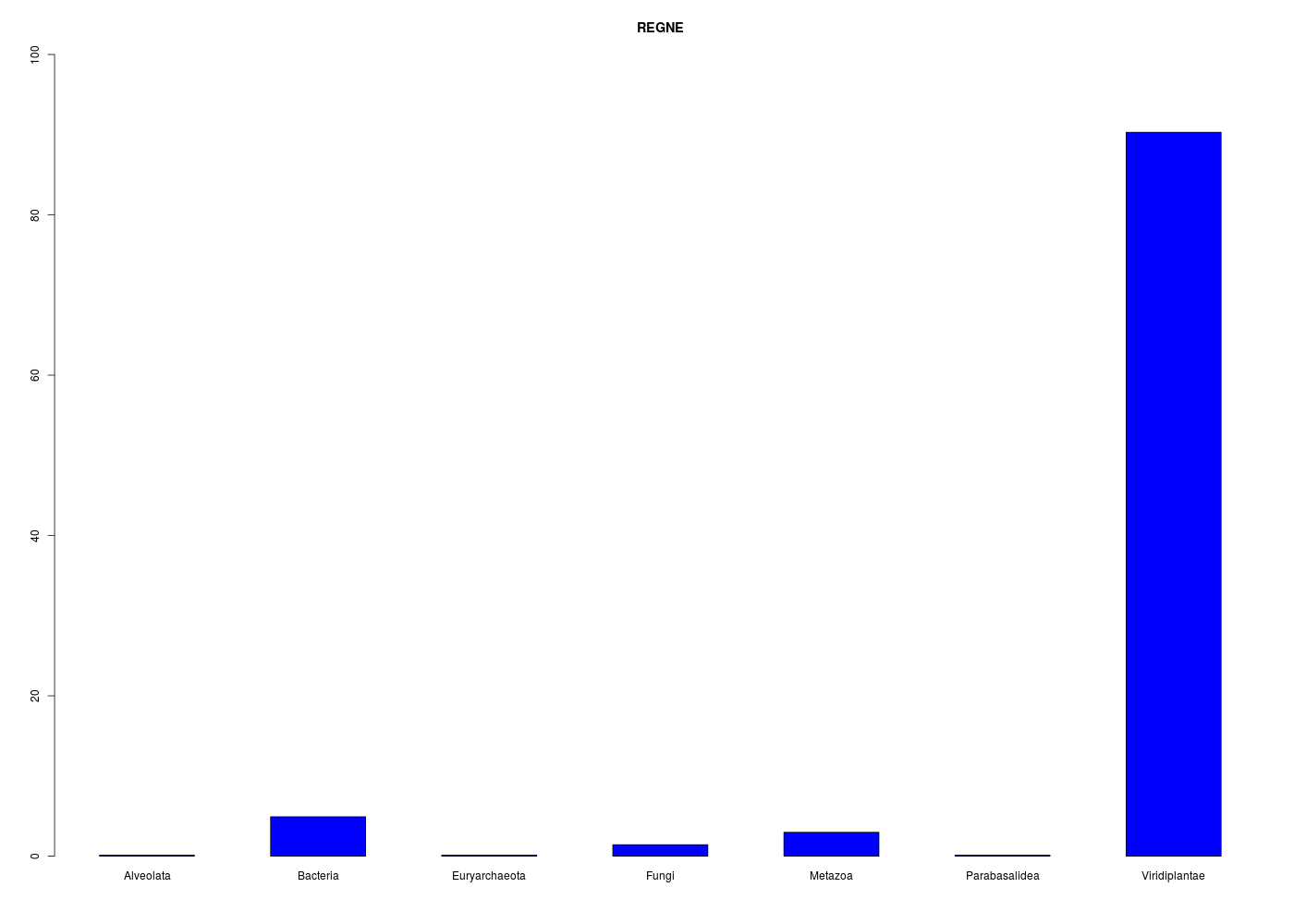
decritQL("REGNE",reign,levels(reign),TRUE)
TRI A PLAT DE : REGNE (ordre des modalités)
Alveolata Bacteria Euryarchaeota Fungi Metazoa Parabasalidea Viridiplantae Total
Effectif 1 38 1 11 23 1 698 773
Cumul Effectif 1 39 40 51 74 75 773 773
Frequence (en %) 0 5 0 1 3 0 90 99
Cumul fréquences 0 5 5 7 10 10 100 99
VARIABLE : REGNE (par fréquence décroissante)
Viridiplantae Bacteria Metazoa Fungi Alveolata Euryarchaeota Parabasalidea Total
Effectif 698 38 23 11 1 1 1 773
Cumul Effectif 1 39 40 51 74 75 773 773
Frequence (en %) 90 5 3 1 0 0 0 99
Cumul fréquences 90 95 98 100 100 100 100 99
On dispose alors d'un rappel de la taille de l'échantillon et l'histogramme est dans une échelle fixe qui va de 0 à 100 %.
En ce qui concerne la conclusion, on peut dire que la très grande majorité des protéines (90 %) correspond au règne végétal (Viridiplantae) avec un petit "pool" de bactéries (5 %) et de métazoaires (3 %). Contextuellement, cela s'explique par le fait que les protéines LEA sont traditionnellement associées aux plantes.
3. Fonctions de base pour analyses univariées de variables quantitatives
Comment est implémentée en R la notion de variable quantitative ? Quelles sont les fonctions R associées ?
Analyser la variable Length dans les données lea.dar. On trouvera des informations sur ces données à l'URL lea.htm. Que peut-on en conclure ?
Tout vecteur numérique est considéré par R comme une variable quantitative. On peut alors utiliser les calculs classiques de moyenne, médiane etc. avec les fonctions mean(), median()... Les graphiques associés sont des tracés de points, des boites à moustaches via les fonctions plot(), boxplot()...
Le calcul direct en R pour la longueur peut se faire avec les instructions suivantes une fois les données chargées et la variable lng définie :
# lecture des données
url <- "http://www.info.univ-angers.fr/~gh/Datasets/lea.dar"
lea <- read.table(url,header=TRUE,row.names=1)
lng <- lea$length
# calculs avec R pour la longueur :
nbp <- length( lng )
# tendance centrale
moy <- mean( lng )
med <- quantile(lng, 0.5)
# dispersion
dis <- var( lng )
ect <- sd( lng )
cdv <- round( 100*(ect/moy) )
qu1 <- quantile(lng, 0.25)
qu3 <- quantile(lng, 0.75)
diq <- qu3 - qu1
# valeurs pour controle
lmi <- min( lng )
lma <- max( lng )
# affichages
cat("Taille de l'échantillon ",nbp," protéines\n")
cat("Moyenne ",moy," aa\n")
cat("Variance ",dis," aa^2\n")
cat("Ecart type ",ect," aa\n")
cat("Coefficient de variation ",cdv," %\n")
cat("Médiane ",med," aa\n")
cat("Premier quartile ",qu1," aa\n")
cat("Troisième quartile ",qu3," aa\n")
cat("Distance inter quartiles ",qu3," aa\n")
cat("Minimum ",lmi," aa\n")
cat("Maximum ",lma," aa\n")
# une fonction résumée disponible sous R
summary(lng)
Et on obtient alors :
Taille de l'échantillon 773 protéines
Moyenne 205.6882 aa
Variance 22109.43 aa^2
Ecart type 148.6924 aa
Coefficient de variation 72 %
Médiane 168 aa
Premier quartile 130 aa
Troisième quartile 236 aa
Distance inter quartiles 236 aa
Minimum 68 aa
Maximum 1864 aa
Min. 1st Qu. Median Mean 3rd Qu. Max.
68.0 130.0 168.0 205.7 236.0 1864.0
Cela fait donc beaucoup de choses à écrire, des affichages de sortie pas forcément mal cadrés, alors que l'idée est simple : on veut juste décrire la variable lng. Pour les tracés associés, on peut écrire :
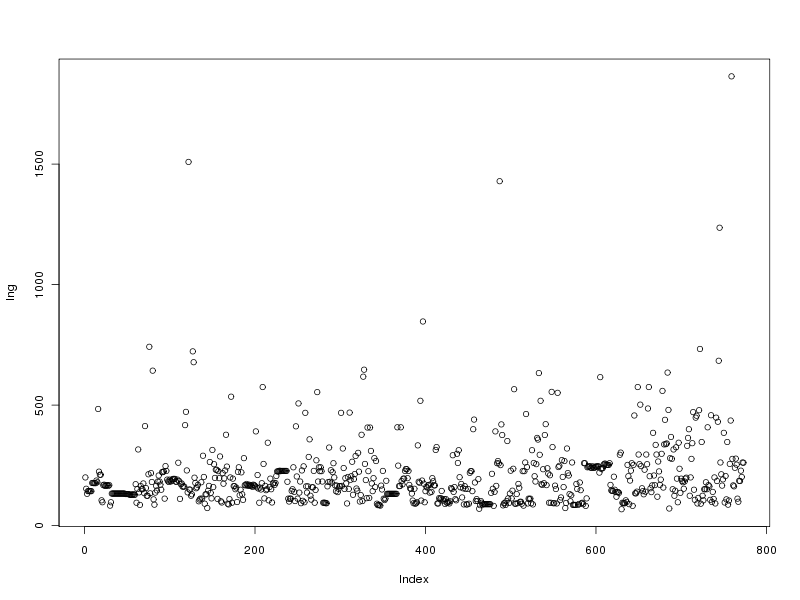
# tracé des valeurs pour la longueur des protéines
plot(lng)
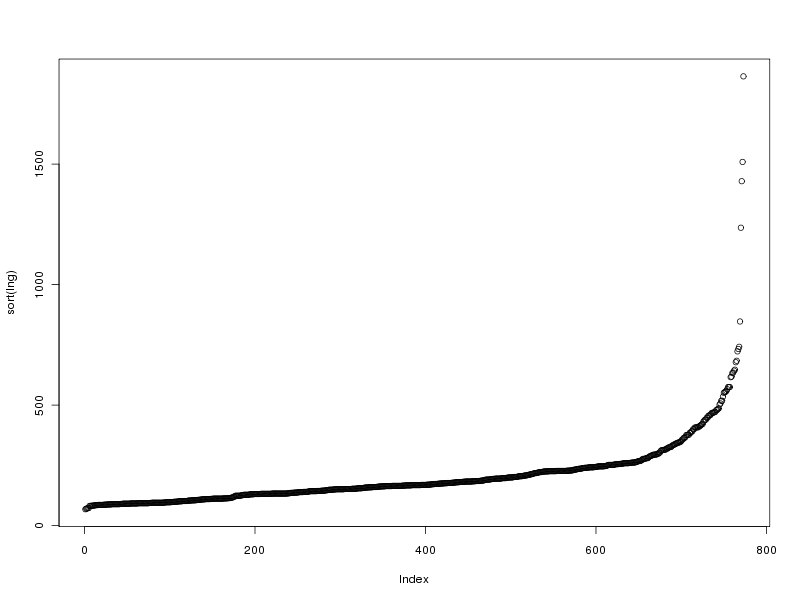
# tracé des valeurs triées
plot(sort(lng))
# histogramme des valeurs par classe (découpage automatique)
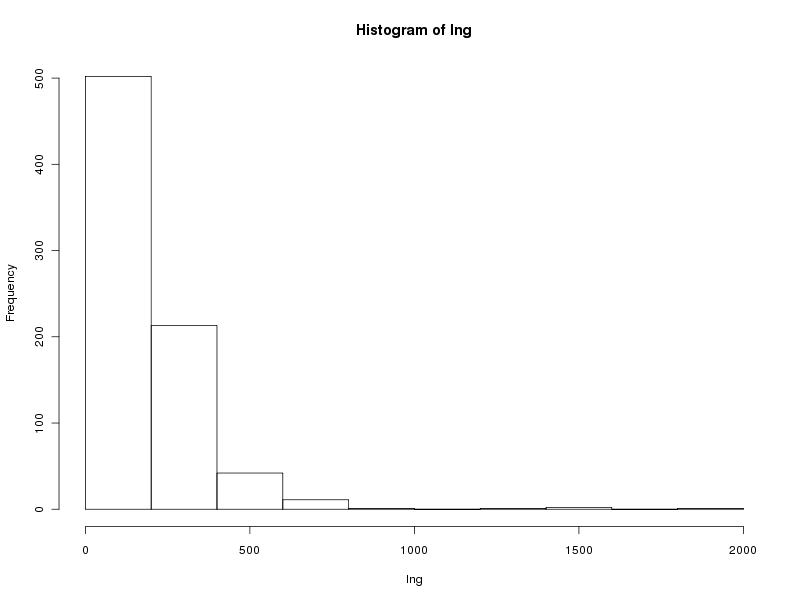
hist(lng)
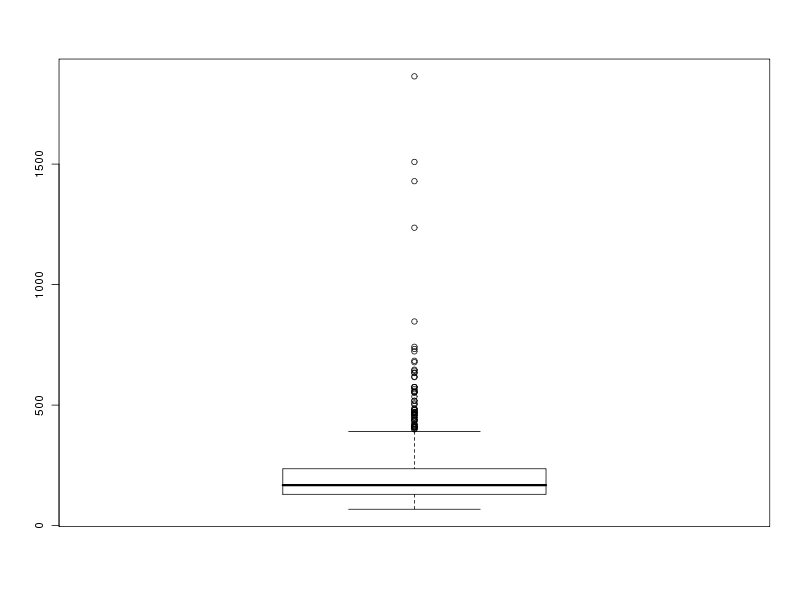
# tracé en boite à moustache
boxplot(lng)
Ce qui fournit les 4 graphiques suivants (cliquables) :
A l'aide des fonctions de statgh.r, tout va beaucoup plus vite à écrire :
# chargement des fonctions gh
source("http://forge.info.univ-angers.fr/~gh/wstat/statgh.r",encoding="latin1")
# lecture des données
url <- "http://www.info.univ-angers.fr/~gh/Datasets/lea.dar"
lea <- lit.dar(url)
lng <- lea$length
# analyse complète de la variable quantitative (calculs et graphiques)
decritQT(
titreQT="Longueur des protéines de LEAPDB",
nomVar=lng,
unite="aa",
graphique=TRUE
) # fin de decritQT
# remarque :
# on aurait pu utiliser, avec de l'habitude, la forme courte :
# decritQT("Longueur des protéines de LEAPDB",lng,"aa",TRUE)
De plus les sorties sont bien présentées, tout est écrit en français et les graphiques sont en couleurs : (sur les graphiques, la moyenne est en rouge, la médiane en vert)
(gH) version 4.87
fonctions d'aides : lit() fqt() fql() ic() fapprox() chi2() fcomp() datagh()
taper aide() pour revoir cette liste
DESCRIPTION STATISTIQUE DE LA VARIABLE Longueur des protéines de LEAPDB
Taille 773 individus
Moyenne 205.6882 aa
Ecart-type 148.6924 aa
Coef. de variation 72 %
1er Quartile 130.0000 aa
Mediane 168.0000 aa
3eme Quartile 236.0000 aa
iqr absolu 106.0000 aa
iqr relatif 63.0000 %
Minimum 68 aa
Maximum 1864 aa
Tracé tige et feuilles
The decimal point is 2 digit(s) to the right of the |
0 | 77777888888899999999999999999999999999999999999999999999999999999999
1 | 00000000000000000000000000000000000000000000000111111111111111111111+323
2 | 00000000000000000000000000001111111111111111222222222222223333333333+107
3 | 000000011111222223333344444445556666788889999
4 | 0011111112223444556666777778889
5 | 0122455667888
6 | 22344588
7 | 234
8 | 5
9 |
10 |
11 |
12 | 4
13 |
14 | 3
15 | 1
16 |
17 |
18 | 6
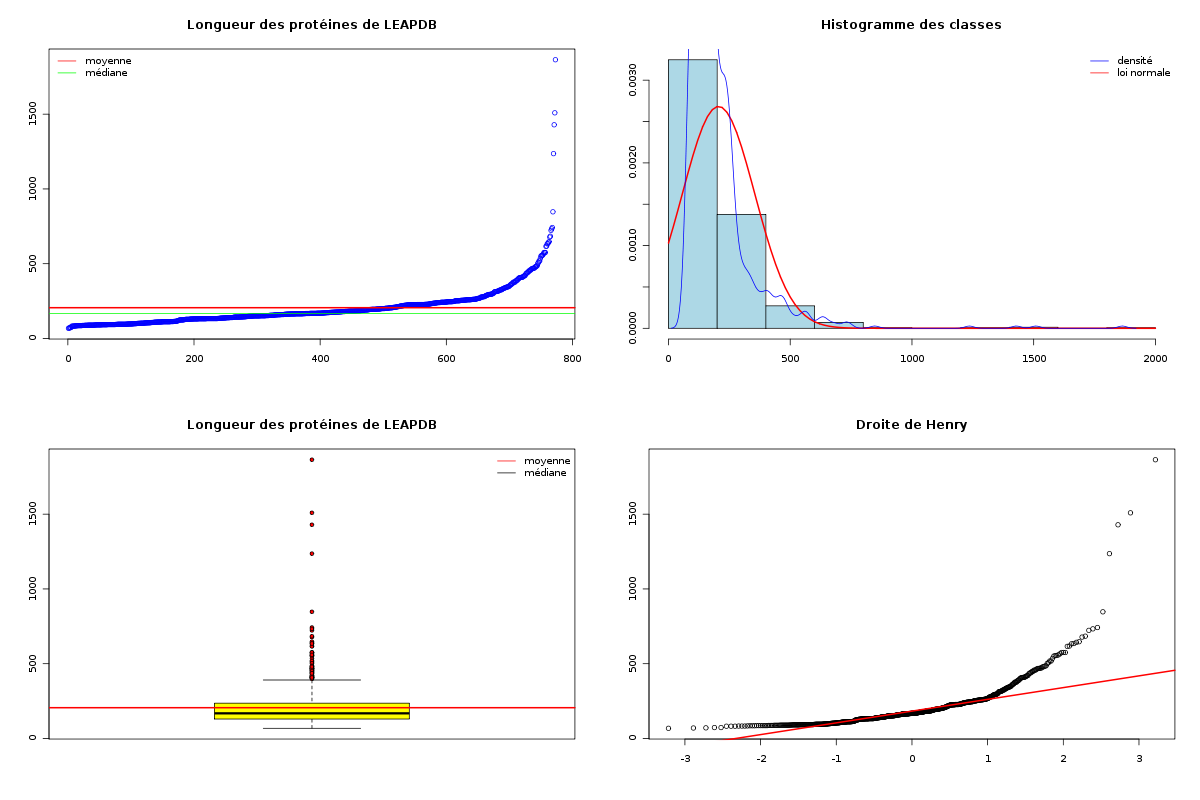
Maintenant que tous les calculs et graphiques sont faits, rappelons-le, les statistiques commencent : il reste à rédiger ce que l'on voit dans ces calculs et graphiques.
La première partie des commentaires est scientifique et objective : elle met en phrases l'information visible dans ces résultats. On pourrait ainsi écrire : la base de données LEAPDB constitue un grand échantillon d'un peu plus de 770 protéines avec une longueur moyenne d'un peu plus de 205 aa (acides aminés) et un écart-type sur la longueur d'environ 150 aa ; les protéines présentes dans la LEAPDB ont, dans les 3/4 des cas une longueur inférieure à 236 aa.
La seconde partie des commentaires est subjective et contextuelle. Elle utilise l'expertise du domaine pour dépasser la première partie. On pourrait ainsi ajouter : ces longueurs sont donc dans une "moyenne raisonnable" de longueurs de protéines, avec toutefois quelques protéines comportant un très grand nombre d'acides aminés.
Concernant la partie subjective, on pourra remarquer que le wiki anglais parle d'une longueur moyenne de 300 aa (sans toutefois citer de source) alors que le wiki français ne dit rien à ce sujet. Un article très intéressant de Brocchieri et Karlin (Nucleic Acids Research, 2005) dont une copie locale est ici permet de mieux comprendre ces valeurs et de distinguer les longueurs des Eucaryotes et Procaryotes. On pourra également consulter les données statistiques du site UniProtKB à la rubrique 3. SEQUENCE SIZE :
http://expasy.org/sprot/relnotes/relstat.html
4. Fonctions de base pour analyses bivariées de variables qualitatives
Analyser séparément puis conjointement les variables PFAM et CDD dans les données lea.dar. On trouvera des informations sur ces données à l'URL lea.htm. Que peut-on en conclure ?
L'étude séparée ou tri à plat et l'étude conjointe ou tri croisé peut se faire directement en R à l'aide de la fonction table() :
# lecture des données
url <- "http://www.info.univ-angers.fr/~gh/Datasets/lea.dar"
lea <- read.table(url,header=TRUE,row.names=1)
# les deux tris à plat
print(table(lea$pfam))
print(table(lea$cdd))
# le tri croisé
print( with(lea,table(cdd,pfam))) # plus court que table(lea$cdd,lea$pfam)
Fichier des résultats
00257 00477 01442 01936 02496 02714 02987 03168 03242 03760 04927 05042 05478 05512 06830 N/A
13 45 1 1 1 3 3 24 38 45 8 1 1 2 7 580
109320 28751 29258 29605 30778 33135 34213 35153 48161 66403 66647 66818 66886
1 3 1 1 3 1 1 1 1 2 3 24 38
67378 68499 68610 69026 69056 70305 80608 81425 84386 84648 84797 85782
45 8 1 1 2 7 1 1 1 10 41 1
86004 88803 88917 91016 92778 N/A
1 2 4 1 9 557
pfam
cdd 00257 00477 01442 01936 02496 02714 02987 03168 03242 03760 04927 05042 05478 05512 06830 N/A
109320 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
28751 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 3
29258 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
29605 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
30778 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 3
33135 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
34213 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
35153 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0
48161 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
66403 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0
66647 0 0 0 0 0 0 3 0 0 0 0 0 0 0 0 0
66818 0 0 0 0 0 0 0 24 0 0 0 0 0 0 0 0
66886 0 0 0 0 0 0 0 0 38 0 0 0 0 0 0 0
67378 0 0 0 0 0 0 0 0 0 45 0 0 0 0 0 0
68499 0 0 0 0 0 0 0 0 0 0 8 0 0 0 0 0
68610 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0
69026 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0
69056 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0
70305 0 0 0 0 0 0 0 0 0 0 0 0 0 0 7 0
80608 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
81425 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
84386 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
84648 10 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
84797 0 41 0 0 0 0 0 0 0 0 0 0 0 0 0 0
85782 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0
86004 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0
88803 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
88917 0 4 0 0 0 0 0 0 0 0 0 0 0 0 0 0
91016 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0
92778 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 9
N/A 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 557
On peut, là encore, préférer nos fonctions triAplat() et triCroise() :
# on récupère les différents PFAM
labelPfam <- as.character(sort(unique(lea$pfam)))
# on utilise notre fonction pour le tri à plat
triAplat(titreQL="PFAM", nomVar=lea$pfam, labelMod=labelPfam )
# idem pour les CDD
labelCdd <- as.character(sort(unique(lea$cdd)))
triAplat(titreQL="CDD", nomVar=lea$cdd, labelMod= labelCdd )
# et voici notre tri croisé
with(lea,triCroise("CDD",cdd,labelCdd,"PFAM",pfam,labelPfam))
Fichier des résultats
TRI A PLAT DE : PFAM
00257 00477 01442 01936 02496 02714 02987 03168 03242 03760 04927 05042 05478 05512 06830 N/A Total
Effectif 13 45 1 1 1 3 3 24 38 45 8 1 1 2 7 580 773
Cumul Effectif 13 58 59 60 61 64 67 91 129 174 182 183 184 186 193 773 773
Frequence (en %) 2 6 0 0 0 0 0 3 5 6 1 0 0 0 1 75 99
Cumul fréquences 2 8 8 8 8 8 9 12 17 23 24 24 24 24 25 100 99
TRI A PLAT DE : CDD
109320 28751 29258 29605 30778 33135 34213 35153 48161 66403 66647 66818 66886 67378 68499 68610
Effectif 1 3 1 1 3 1 1 1 1 2 3 24 38 45 8 1
Cumul Effectif 1 4 5 6 9 10 11 12 13 15 18 42 80 125 133 134
Frequence (en %) 0 0 0 0 0 0 0 0 0 0 0 3 5 6 1 0
Cumul fréquences 0 1 1 1 1 1 1 2 2 2 2 5 10 16 17 17
69026 69056 70305 80608 81425 84386 84648 84797 85782 86004
Effectif 1 2 7 1 1 1 10 41 1 1
Cumul Effectif 135 137 144 145 146 147 157 198 199 200
Frequence (en %) 0 0 1 0 0 0 1 5 0 0
Cumul fréquences 17 18 19 19 19 19 20 26 26 26
88803 88917 91016 92778 N/A Total
Effectif 2 4 1 9 557 773
Cumul Effectif 202 206 207 216 773 773
Frequence (en %) 0 1 0 1 72 96
Cumul fréquences 26 27 27 28 100 96
TRI CROISE DES QUESTIONS :
CDD (en ligne)
PFAM (en colonne)
Effectifs
00257 00477 01442 01936 02496 02714 02987 03168 03242 03760 04927 05042 05478 05512 06830 N/A
109320 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
28751 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 3
29258 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
29605 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
30778 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 3
33135 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
34213 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
35153 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0
48161 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
66403 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0
66647 0 0 0 0 0 0 3 0 0 0 0 0 0 0 0 0
66818 0 0 0 0 0 0 0 24 0 0 0 0 0 0 0 0
66886 0 0 0 0 0 0 0 0 38 0 0 0 0 0 0 0
67378 0 0 0 0 0 0 0 0 0 45 0 0 0 0 0 0
68499 0 0 0 0 0 0 0 0 0 0 8 0 0 0 0 0
68610 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0
69026 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0
69056 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0
70305 0 0 0 0 0 0 0 0 0 0 0 0 0 0 7 0
80608 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
81425 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
84386 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
84648 10 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
84797 0 41 0 0 0 0 0 0 0 0 0 0 0 0 0 0
85782 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0
86004 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0
88803 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
88917 0 4 0 0 0 0 0 0 0 0 0 0 0 0 0 0
91016 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0
92778 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 9
N/A 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 557
Effectifs avec totaux
00257 00477 01442 01936 02496 02714 02987 03168 03242 03760 04927 05042 05478 05512 06830 N/A Total
109320 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
28751 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 3 3
29258 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1
29605 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1
30778 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 3 3
33135 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1
34213 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1
35153 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1
48161 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1
66403 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 2
66647 0 0 0 0 0 0 3 0 0 0 0 0 0 0 0 0 3
66818 0 0 0 0 0 0 0 24 0 0 0 0 0 0 0 0 24
66886 0 0 0 0 0 0 0 0 38 0 0 0 0 0 0 0 38
67378 0 0 0 0 0 0 0 0 0 45 0 0 0 0 0 0 45
68499 0 0 0 0 0 0 0 0 0 0 8 0 0 0 0 0 8
68610 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1
69026 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1
69056 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 2
70305 0 0 0 0 0 0 0 0 0 0 0 0 0 0 7 0 7
80608 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1
81425 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1
84386 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1
84648 10 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 10
84797 0 41 0 0 0 0 0 0 0 0 0 0 0 0 0 0 41
85782 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1
86004 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1
88803 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2
88917 0 4 0 0 0 0 0 0 0 0 0 0 0 0 0 0 4
91016 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1
92778 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 9 9
N/A 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 557 557
Total 13 45 1 1 1 3 3 24 38 45 8 1 1 2 7 580 773
Valeurs en % du total
00257 00477 01442 01936 02496 02714 02987 03168 03242 03760 04927 05042 05478 05512 06830 N/A TOTAL
109320 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
28751 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
29258 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
29605 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
30778 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
33135 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
34213 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
35153 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
48161 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
66403 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
66647 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
66818 0 0 0 0 0 0 0 3 0 0 0 0 0 0 0 0 3
66886 0 0 0 0 0 0 0 0 5 0 0 0 0 0 0 0 5
67378 0 0 0 0 0 0 0 0 0 6 0 0 0 0 0 0 6
68499 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1
68610 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
69026 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
69056 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
70305 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1
80608 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
81425 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
84386 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
84648 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
84797 0 5 0 0 0 0 0 0 0 0 0 0 0 0 0 0 5
85782 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
86004 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
88803 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
88917 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
91016 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
92778 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1
N/A 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 72 72
TOTAL 2 6 0 0 0 0 0 3 5 6 1 0 0 0 1 75 100
On peut en conclure (rapidement) deux choses. D'abord, il y a vraiment beaucoup de données manquantes (75 % pour PFAM, 72 % pour CDD). Ensuite, pour les PFAM et CDD renseignés, que ces informations ont l'air liées ou dépendantes puisqu'on voit apparaitre des bandes diagonales dans le tri croisé. On peut le voir nettement dans l'extrait ci-dessous du tri croisé où les zéros ont été remplacés par un point :
35153 66403 66647 66818 66886 67378 68499 68610 69026 69056 70305 84648
257 . . . . . . . . . . .
477 . . . . . . . . . . .
1442 . . . . . . . . . . .
1936 . . . . . . . . . . .
2496 . . . . . . . . . . .
2714 1 2 . . . . . . . . .
2987 . . 3 . . . . . . . .
3168 . . . 24 . . . . . . .
3242 . . . . 38 . . . . . .
3760 . . . . . 45 . . . . .
4927 . . . . . . 8 . . . .
5042 . . . . . . . 1 . . .
5478 . . . . . . . . 1 . .
5512 . . . . . . . . . 2 .
6830 . . . . . . . . . . 7
5. Fonctions de base pour analyses bivariées de variables quantitatives
On s'intéresse aux données IRIS. Etudier séparément puis conjointement les variables PE_L et PE_W. Que peut-on en conclure ?
Voici sans explication le code R que nous proposons :
# chargement des fonctions gh et lecture des données
source("http://forge.info.univ-angers.fr/~gh/wstat/statgh.r",encoding="latin1")
iris <- lit.dar("http://forge.info.univ-angers.fr/~gh/Datasets/iris.dar")
# analyse séparée de PE_L et de PE_W
decritQT("longueur pétales",iris$PE_L,"mm",TRUE)
decritQT("largeur pétales",iris$PE_W,"mm",TRUE)
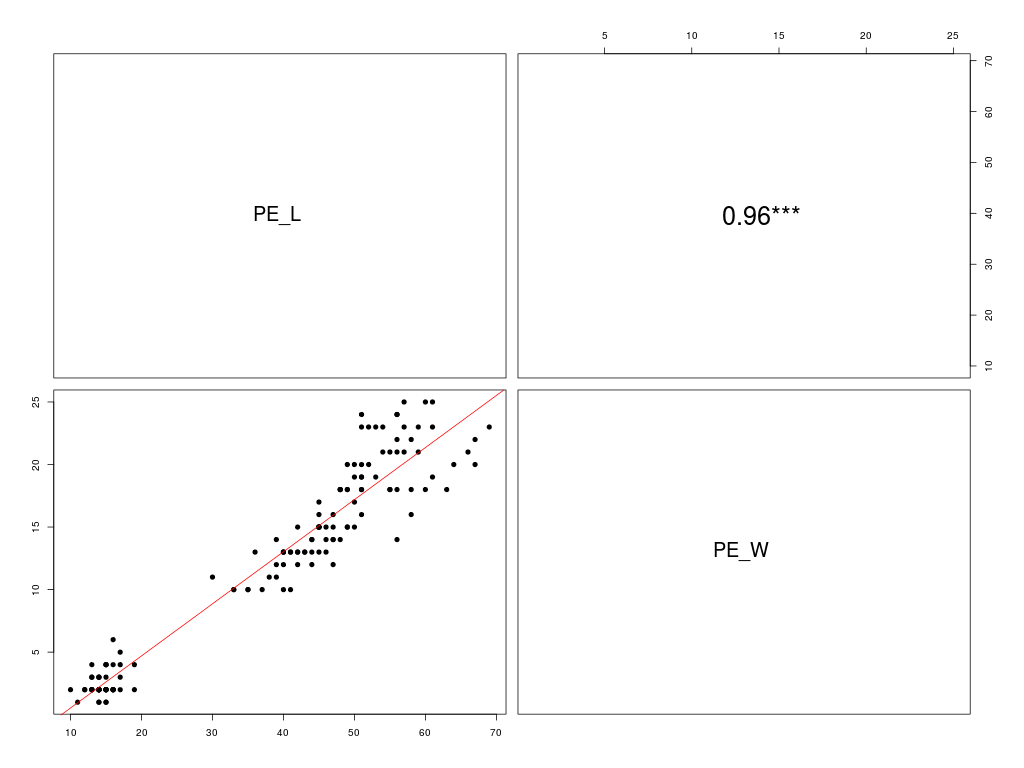
# analyse conjointe PE_L et de PE_W
vars <- c("PE_L","PE_W")
data <- iris[,vars]
allQT(data,vars,rep("mm",2),TRUE)
(gH) version 4.87
fonctions d'aides : lit() fqt() fql() ic() fapprox() chi2() fcomp() datagh()
taper aide() pour revoir cette liste
DESCRIPTION STATISTIQUE DE LA VARIABLE longueur pétales
Taille 149 individus
Moyenne 37.7315 mm
Ecart-type 17.6143 mm
Coef. de variation 47 %
1er Quartile 16.0000 mm
Mediane 44.0000 mm
3eme Quartile 51.0000 mm
iqr absolu 35.0000 mm
iqr relatif 80.0000 %
Minimum 10 mm
Maximum 69 mm
Tracé tige et feuilles
The decimal point is 1 digit(s) to the right of the |
1 | 012233333334444444444444
1 | 5555555555556666666777799
2 |
2 |
3 | 033
3 | 55678999
4 | 000001112222334444
4 | 5555555566677777888899999
5 | 000011111111223344
5 | 55566666677788899
6 | 0011134
6 | 6779
DESCRIPTION STATISTIQUE DE LA VARIABLE largeur pétales
Taille 149 individus
Moyenne 12.0805 mm
Ecart-type 7.6153 mm
Coef. de variation 63 %
1er Quartile 3.0000 mm
Mediane 13.0000 mm
3eme Quartile 18.0000 mm
iqr absolu 15.0000 mm
iqr relatif 115.0000 %
Minimum 1 mm
Maximum 25 mm
Tracé tige et feuilles
The decimal point is at the |
1 | 00000
2 | 0000000000000000000000000000
3 | 0000000
4 | 0000000
5 | 0
6 | 0
7 |
8 |
9 |
10 | 0000000
11 | 000
12 | 00000
13 | 0000000000000
14 | 00000000
15 | 00000000000
16 | 0000
17 | 00
18 | 0000000000000
19 | 00000
20 | 000000
21 | 000000
22 | 000
23 | 00000000
24 | 000
25 | 000
Voici les 10 premières lignes de données (il y en a 149 en tout)
PE_L PE_W
i001_SETOSA 14 2
i002_VIRGINICA 56 22
i003_VERSICOLOR 46 15
i004_VIRGINICA 56 24
i005_VIRGINICA 51 18
i006_SETOSA 14 3
i007_VIRGINICA 51 23
i008_VERSICOLOR 45 15
i009_VERSICOLOR 48 18
i010_SETOSA 10 2
Description des 2 variables statistiques par cdv décroissant
Num Nom Taille Moyenne Unite Ecart-type Coef. de var. Minimum Maximum
2 PE_W 149 12.081 mm 7.615 63.04 % 1.000 25.000
1 PE_L 149 37.732 mm 17.614 46.68 % 10.000 69.000
Par ordre d'entrée
Num Nom Taille Moyenne Unite Ecart-type Coef. de var. Minimum Maximum
1 PE_L 149 37.732 mm 17.614 46.68 % 10.000 69.000
2 PE_W 149 12.081 mm 7.615 63.04 % 1.000 25.000
Par moyenne décroissante
Num Nom Taille Moyenne Unite Ecart-type Coef. de var. Minimum Maximum
1 PE_L 149 37.732 mm 17.614 46.68 % 10.000 69.000
2 PE_W 149 12.081 mm 7.615 63.04 % 1.000 25.000
Matrice des corrélations au sens de Pearson pour 149 lignes et 2 colonnes
PE_L PE_W
PE_L 1.000
PE_W 0.963 1.000
Meilleure corrélation 0.9629571 pour PE_W et PE_L p-value 0
Formules PE_L = 2.227 * PE_W + 10.824
et PE_W = 0.416 * PE_L -3.628
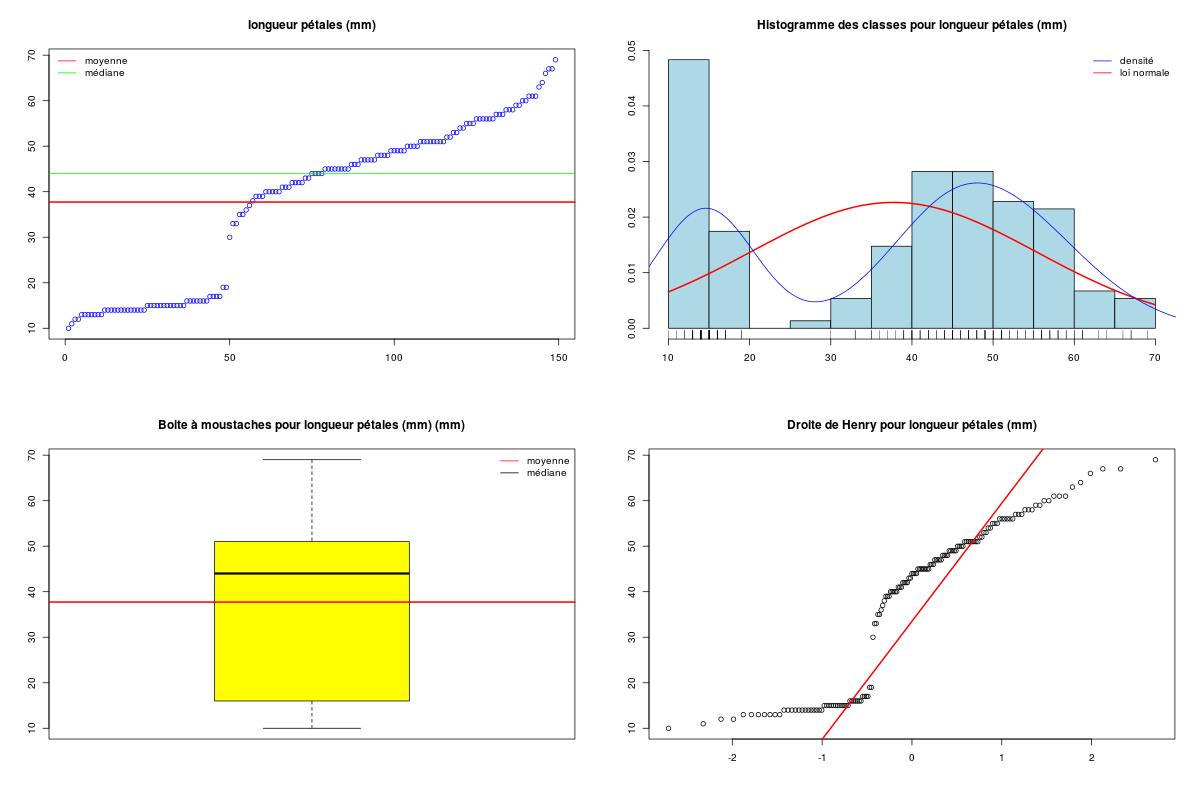
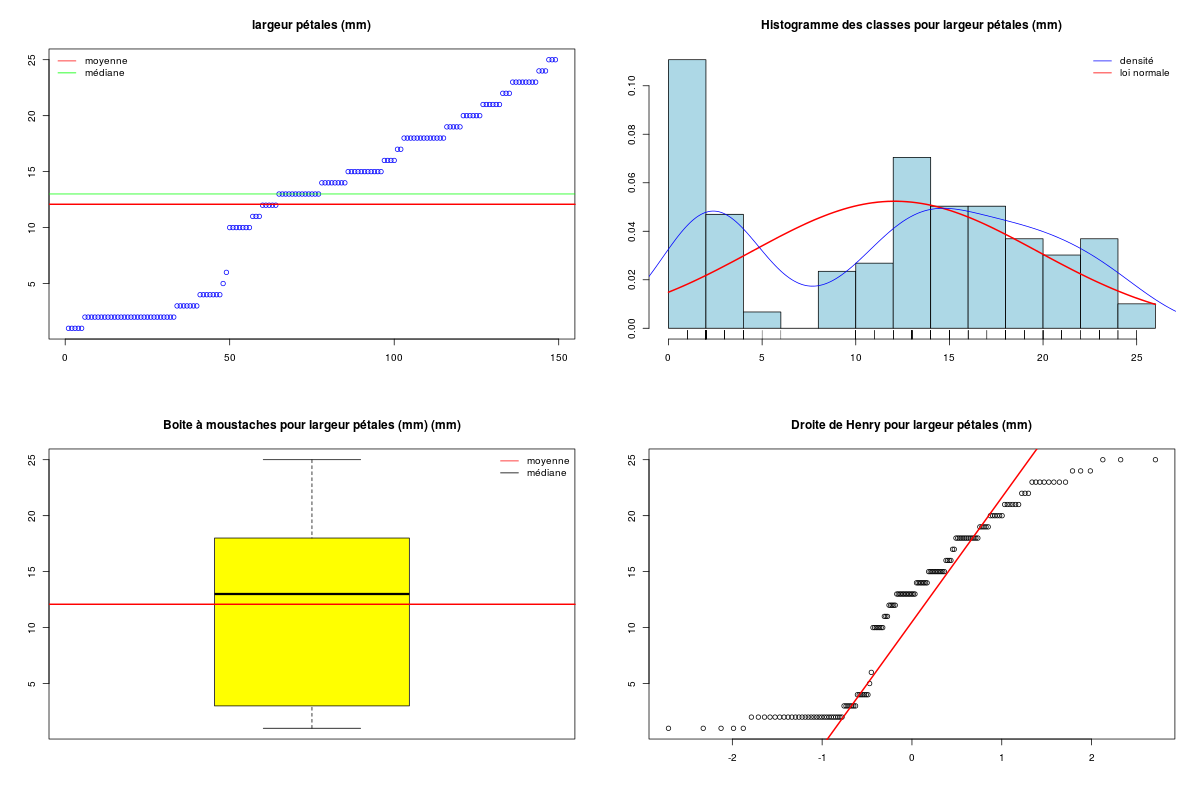
On constate que les deux variables en sont pas distribuées normalement et qu'elles semblent plutôt toutes deux bimodales. De plus l'analyse de la corrélation linéaire entre ces deux variables montre un fort lien linéaire (ρ=0,96). Les formules de liaison sont fournies dans la sortie précédente, fichier iris.res.
6. Utilisation des packages stats et graphics
Que contiennent les packages stats et graphics ?
Est-il facile de connaitre et maitriser l'ensemble des fonctions de ces deux packages ?
Ces deux packages contiennent beaucoup de fonctions. On pourra utiliser notre fonction lls() pour constater qu'il y a respectivement 446 et 87 objets dans ces packages, dont la plupart sont des fonctions. On trouvera dans les fichiers lls_stats.sor et lls_graphics.sor la liste triée de ces objets. Il est donc illusoire de vouloir maitriser rapidement ces deux packages, surtout si on se rappelle que la plupart des fonctions ont de nombreux paramètres, des valeurs par défaut...
# chargement des fonctions gh
source("http://forge.info.univ-angers.fr/~gh/wstat/statgh.r",encoding="latin1")
# listage des objets des packages stats et graphics :
lls("stats")
lls("graphics")
7. Formats graphiques et exports pour publication
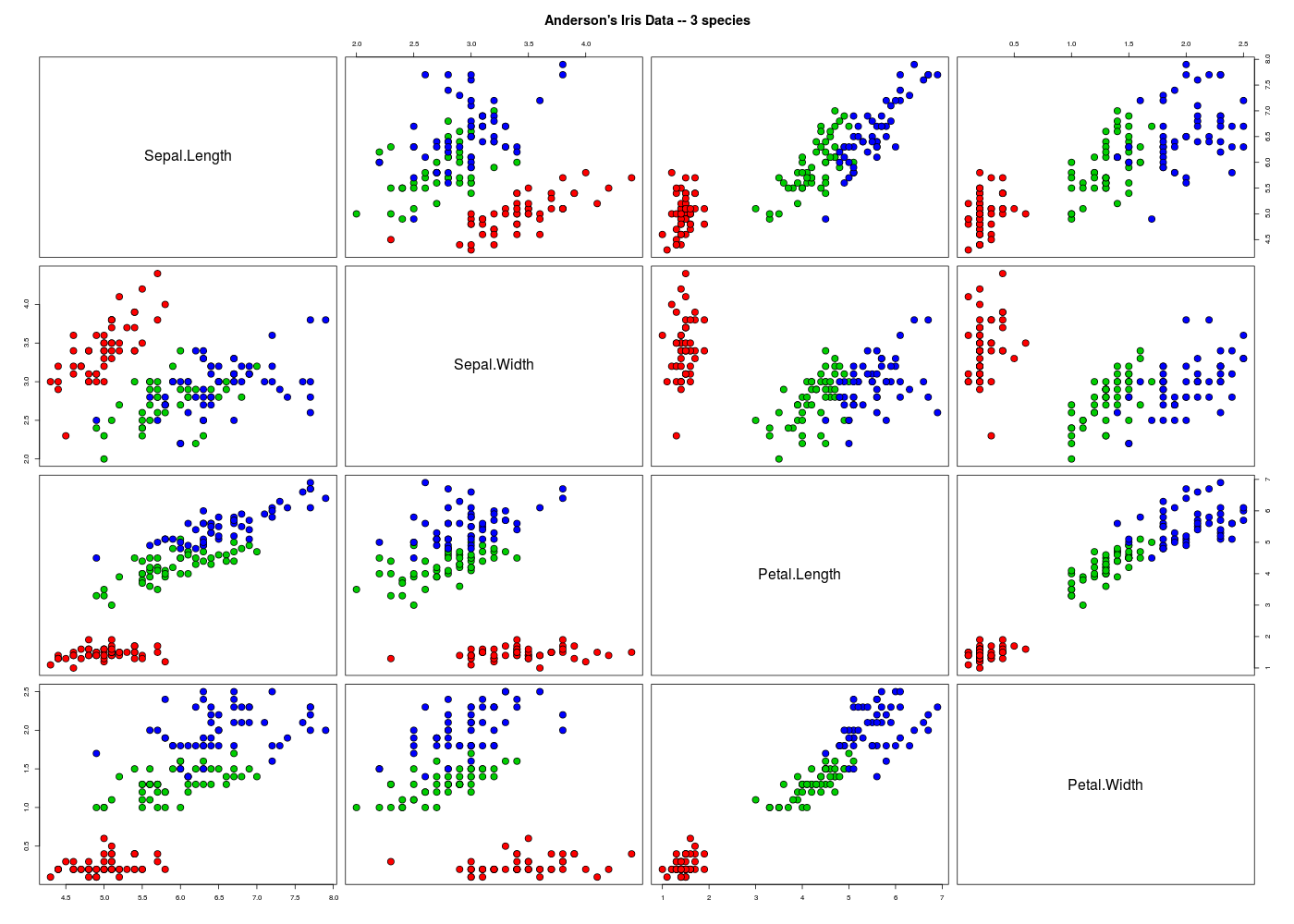
On voudrait maintenant exporter le tracé colorisé par paires de R pour les données quantitatives des "vraies" données IRIS, soit le graphique ci-dessous :

Comment reproduire ce graphique ? Comment l'exporter afin de l'insérer dans un document Word, Excel, LaTeX ou XHTML ? On utilisera l'instruction data(iris) pour charger les données.
Les graphiques par paires sont générés en R par la fonction pairs() du package graphics. L'utilisation des exemples en ligne via example(pairs) donne la solution pour produire le graphique demandé.
Si on veut exporter dans plusieurs formats le graphique, le mieux est de faire, là encore, une fonction des instructions de tracé (plutôt qu'un copier/coller) puis d'insérer autour de l'appel de cette fonction les instructions d'export, à savoir l'appel des fonctions png(), pdf() et postscript() en ouverture et de la seule fonction dev.off() en fermeture.
#######################################################################
plotiris <- function(...) {
#######################################################################
pairs(
x = iris[1:4],
main = "Anderson's Iris Data -- 3 species",
pch = 21,
bg = c("red", "green3", "blue")[unclass(iris$Species)],
...
) # fin de pairs
} # fin de fonction plotiris
#######################################################################
# production d'un fichier PNG pour Word, Excel et XHTML
png(filename="iris.png",width=1400,height=1000) # fonction gh : gr("iris.png")
plotiris(cex=2)
dev.off()
# production d'un fichier PDF pour LaTeX
pdf("iris.pdf")
plotiris(cex=3)
dev.off()
# production d'un fichier PS (postscript) pour LaTeX
postscript("iris.ps")
plotiris()
dev.off()
On pourra consulter sous les liens les fichiers iris.pdf et iris.ps à condition de disposer pour ce dernier fichier d'un visualiseur PostScript.
Code-source php de cette page. Retour à la page principale du cours.
|
 Retour à la page principale de
(gH)
Retour à la page principale de
(gH)