1. Types de graphiques et philosophie des graphiques en R
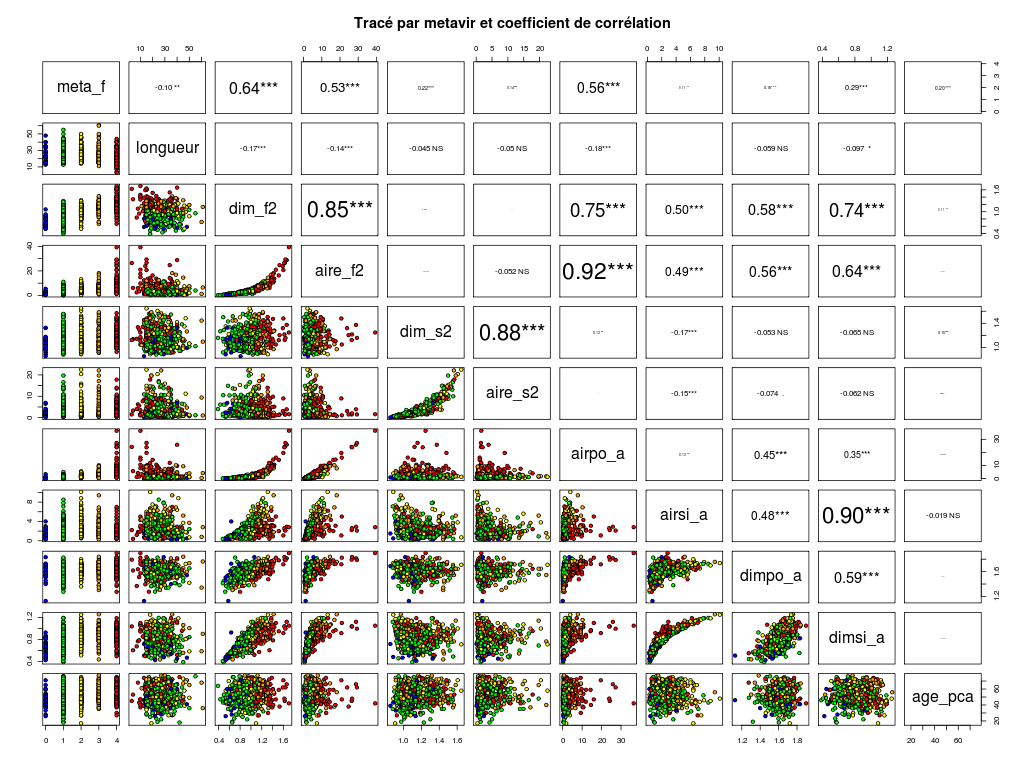
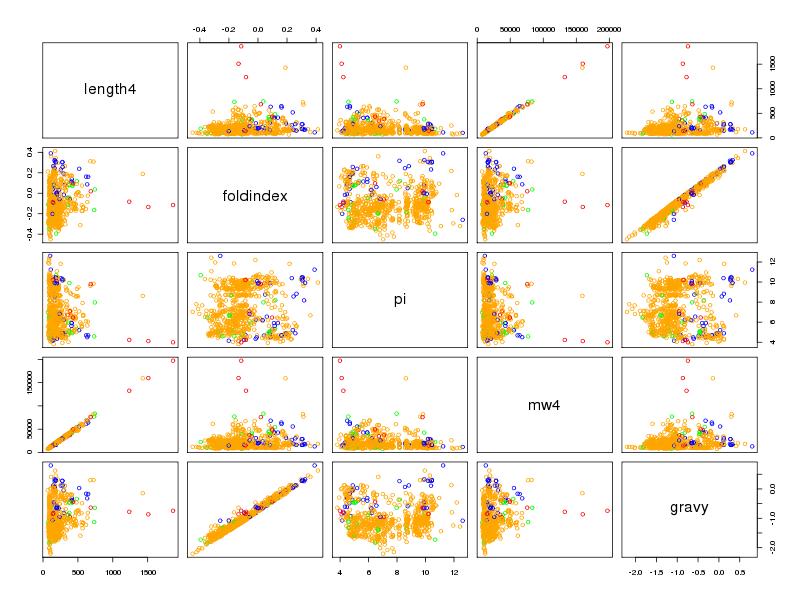
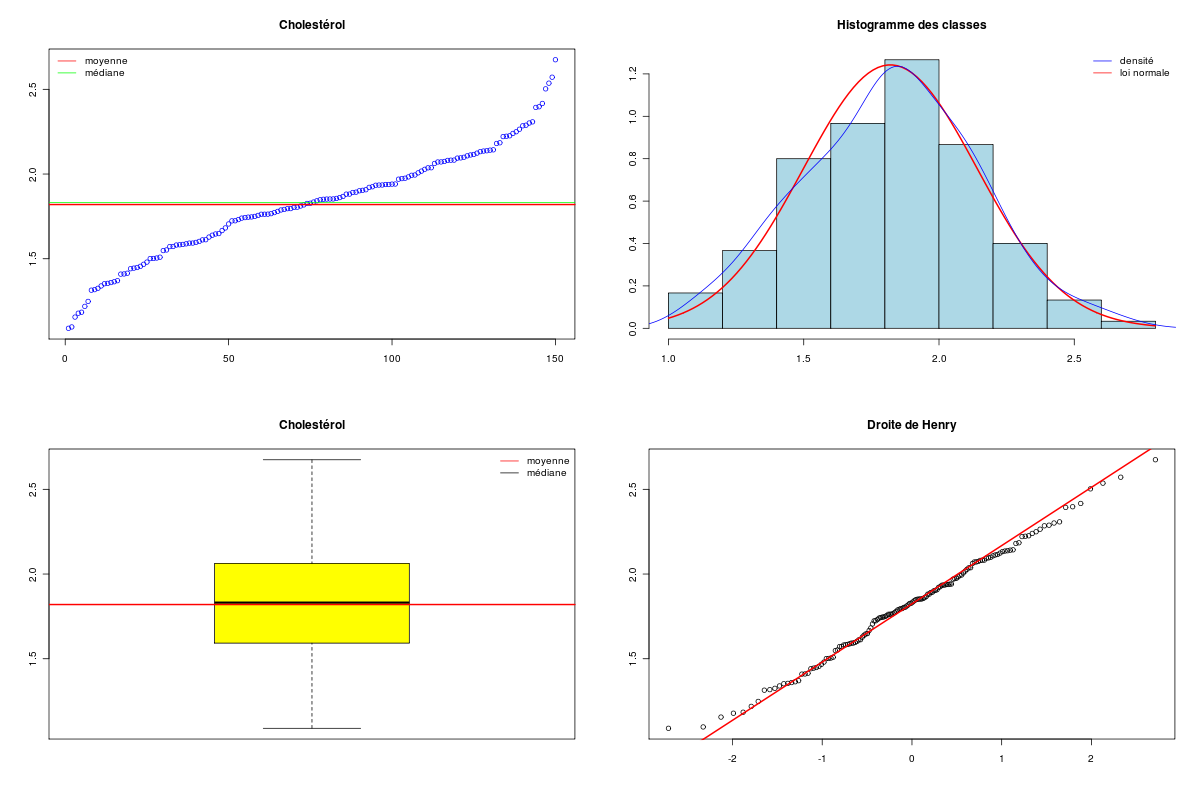
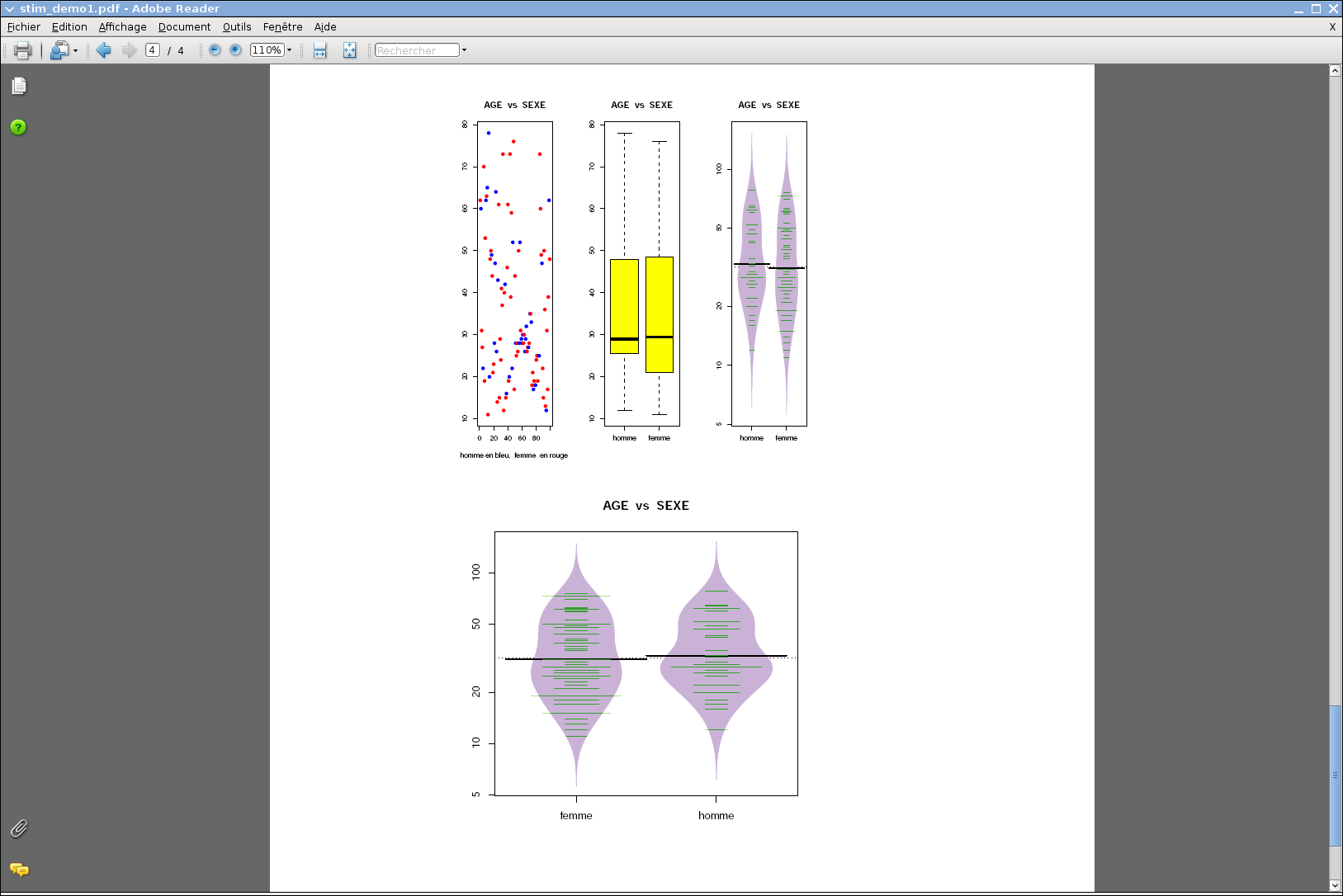
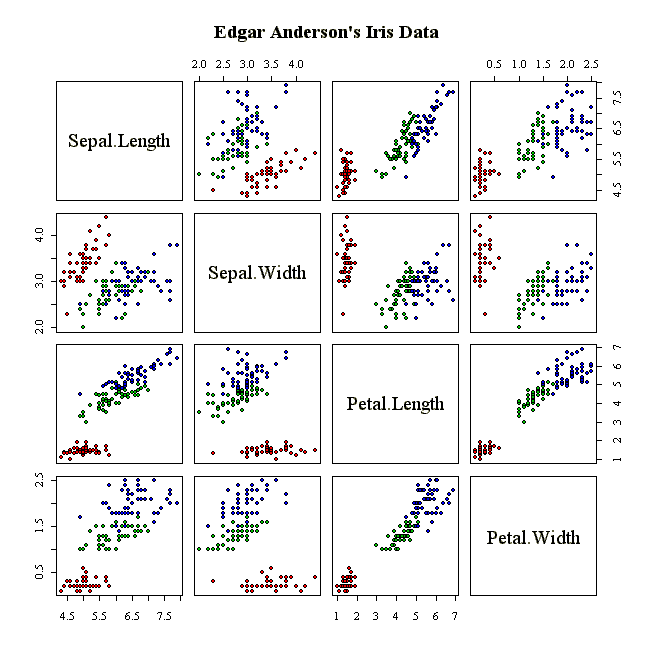
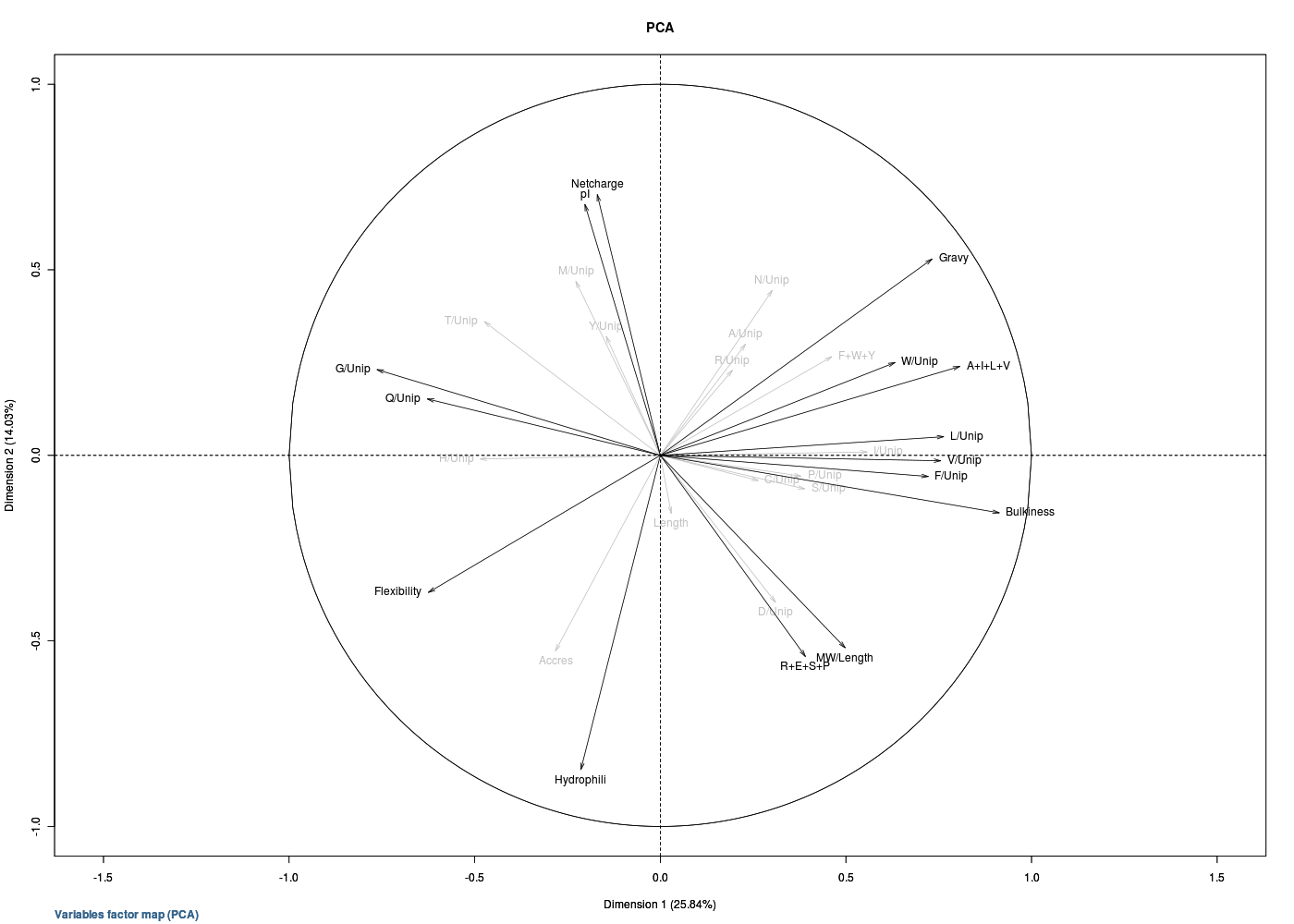
Quel type de graphiques peut-on tracer en R ? Où peut-on voir des exemples de tracés sophistiqués en R ? Savez-vous nommer tous les graphiques ci-dessous ?
Quelles sont les options de la fonction plot() ? Où sont stockées les valeurs par défaut pour les graphiques en R ? Comment modifier une option puis remettre la valeur par défaut ?
R peut tout tracer tous les types de graphiques existants. Voici quelques noms de fonctions évocateurs avec indication du package associé :
Le site R Graph Gallery met en ligne plusieurs milliers de graphiques produits via R. Sur ce site, cliquer sur une image mène au code R pour reproduire le graphique. Ce site donne une bonne vue de la capacité de R à produire des graphiques sophistiqués.
La fonction plot() fait partie du package graphics qui contient moins d'une centaine de fonctions. C'est une fonction dite générique qui sert de point d'entrée à d'autres fonctions comme plot.factor(), plot.formula(), plot.function(), plot.histogram(), plot.table() et plot.window() afin d'interfacer plot.xy().
Un copier/coller sous R du code suivant permet de voir chacune des fonctions plot.* en action (graphiques non reproduits ici) :
example(plot)
example(plot.factor)
example(plot.formula)
example(plot.function)
example(plot.histogram)
example(plot.table)
example(plot.window)
example(plot.xy)
> example(plot)
plot> require(stats)
plot> plot(cars)
plot> lines(lowess(cars))
plot> plot(sin, -pi, 2*pi) # see ?plot.function
plot> ## Discrete Distribution Plot:
plot> plot(table(rpois(100, 5)), type = "h", col = "red", lwd = 10,
plot+ main = "rpois(100, lambda = 5)")
plot> ## Simple quantiles/ECDF, see ecdf() {library(stats)} for a better one:
plot> plot(x <- sort(rnorm(47)), type = "s", main = "plot(x, type = \"s\")")
plot> points(x, cex = .5, col = "dark red")
> example(plot.factor)
plt.fc> require(grDevices)
plt.fc> plot(weight ~ group, data = PlantGrowth) # numeric vector ~ factor
plt.fc> plot(cut(weight, 2) ~ group, data = PlantGrowth) # factor ~ factor
plt.fc> ## passing "..." to spineplot() eventually:
plt.fc> plot(cut(weight, 3) ~ group, data = PlantGrowth,
plt.fc+ col = hcl(c(0, 120, 240), 50, 70))
plt.fc> plot(PlantGrowth$group, axes = FALSE, main = "no axes") # extremely silly
> example(plot.formula)
plt.fr> op <- par(mfrow = c(2,1))
plt.fr> plot(Ozone ~ Wind, data = airquality, pch = as.character(Month))
plt.fr> plot(Ozone ~ Wind, data = airquality, pch = as.character(Month),
plt.fr+ subset = Month != 7)
plt.fr> par(op)
plt.fr> ## text.formula() can be very natural:
plt.fr> wb <- within(warpbreaks, {
plt.fr+ time <- seq_along(breaks); W.T <- wool:tension })
plt.fr> plot(breaks ~ time, data = wb, type = "b")
plt.fr> text(breaks ~ time, data = wb, label = W.T, col = 1+as.integer(wool))
> example(plot.function)
plt.fn> plot(qnorm) # default range c(0, 1) is appropriate here,
plt.fn> # but end values are -/+Inf and so are omitted.
plt.fn> plot(qlogis, main = "The Inverse Logit : qlogis()")
plt.fn> abline(h = 0, v = 0:2/2, lty = 3, col = "gray")
plt.fn> curve(sin, -2*pi, 2*pi, xname = "t")
plt.fn> curve(tan, xname = "t", add = NA,
plt.fn+ main = "curve(tan) --> same x-scale as previous plot")
plt.fn> op <- par(mfrow = c(2, 2))
plt.fn> curve(x^3 - 3*x, -2, 2)
plt.fn> curve(x^2 - 2, add = TRUE, col = "violet")
plt.fn> ## simple and advanced versions, quite similar:
plt.fn> plot(cos, -pi, 3*pi)
plt.fn> curve(cos, xlim = c(-pi, 3*pi), n = 1001, col = "blue", add = TRUE)
plt.fn> chippy <- function(x) sin(cos(x)*exp(-x/2))
plt.fn> curve(chippy, -8, 7, n = 2001)
plt.fn> plot (chippy, -8, -5)
plt.fn> for(ll in c("", "x", "y", "xy"))
plt.fn+ curve(log(1+x), 1, 100, log = ll, sub = paste0("log = '", ll, "'"))
plt.fn> par(op)
> example(plot.histogram)
plt.hs> (wwt <- hist(women$weight, nclass = 7, plot = FALSE))
$breaks
[1] 115 120 125 130 135 140 145 150 155 160 165
$counts
[1] 3 1 2 2 1 1 2 1 1 1
$density
[1] 0.04000000 0.01333333 0.02666667 0.02666667 0.01333333 0.01333333 0.02666667 0.01333333 0.01333333 0.01333333
$mids
[1] 117.5 122.5 127.5 132.5 137.5 142.5 147.5 152.5 157.5 162.5
$xname
[1] "women$weight"
$equidist
[1] TRUE
attr(,"class")
[1] "histogram"
plt.hs> plot(wwt, labels = TRUE) # default main & xlab using wwt$xname
plt.hs> plot(wwt, border = "dark blue", col = "light blue",
plt.hs+ main = "Histogram of 15 women's weights", xlab = "weight [pounds]")
plt.hs> ## Fake "lines" example, using non-default labels:
plt.hs> w2 <- wwt; w2$counts <- w2$counts - 1
plt.hs> lines(w2, col = "Midnight Blue", labels = ifelse(w2$counts, "> 1", "1"))
> example(plot.table)
plt.tb> ## 1-d tables
plt.tb> (Poiss.tab <- table(N = stats::rpois(200, lambda = 5)))
N
0 1 2 3 4 5 6 7 8 9 10 11
2 6 21 21 41 31 23 26 13 6 8 2
plt.tb> plot(Poiss.tab, main = "plot(table(rpois(200, lambda = 5)))")
plt.tb> plot(table(state.division))
plt.tb> ## 4-D :
plt.tb> plot(Titanic, main ="plot(Titanic, main= *)")
> example(plot.window)
plt.wn> ##--- An example for the use of 'asp' :
plt.wn> require(stats) # normally loaded
plt.wn> loc <- cmdscale(eurodist)
plt.wn> rx <- range(x <- loc[,1])
plt.wn> ry <- range(y <- -loc[,2])
plt.wn> plot(x, y, type = "n", asp = 1, xlab = "", ylab = "")
plt.wn> abline(h = pretty(rx, 10), v = pretty(ry, 10), col = "lightgray")
plt.wn> text(x, y, labels(eurodist), cex = 0.8)
> example(plot.xy)
plt.xy> points.default # to see how it calls "plot.xy(xy.coords(x, y), ...)"
function (x, y = NULL, type = "p", ...)
plot.xy(xy.coords(x, y), type = type, ...)
<bytecode: 0x7409108>
<environment: namespace:graphics>
Il existe beaucoup trop de fonctions plot induites pour pouvoir les présenter ici car toute classe d'objets implémente en général sa fonction print, sa fonction plot et sa fonction summary. Citons seulement celles du package stats :
plot.acf
plot.dendrogram
plot.density
plot.ecdf
plot.hclust
plot.isoreg
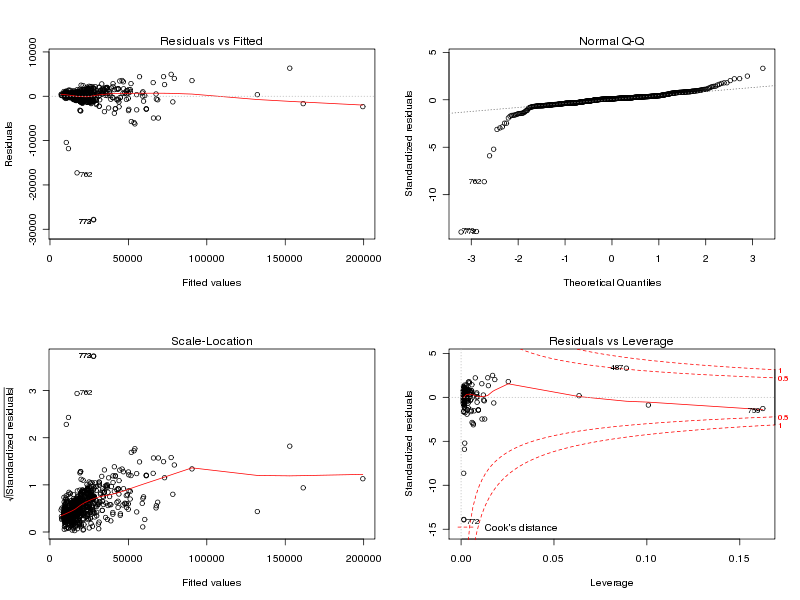
plot.lm
plot.mlm
plot.ppr
plot.prcomp
plot.spec
plot.spec.coherency
plot.spec.phase
plot.stepfun
plot.stl
plot.ts
plot.tskernel
plot.TukeyHSD
La philosophie de R en ce qui concerne les graphiques en mode standard est d'autoriser un maximum de souplesse à travers des valeurs par défaut et des interfaces pour des primitives. Ainsi plot(main="Tracé"...) dit à plot() que le titre principal de la figure est Tracé mais on aurait pu, après avoir tracé avec plot(), utiliser la fonction title() via title(main="Tracé").
De nombreux paramètres graphiques sont disponibles avec la fonction par(). Il suffit de taper example(par) sous R pour voir une partie de l'utilisation de ces paramètres. La liste des paramètres graphiques, fournie par par(), n'est pas très facile à comprendre, ni à mémoriser, car de nombreuses données sont des abbréviations américaines, comme cex pour Character EXtension (facteur d'expansion de la taille des caractères) ou omi pour Outer Margin in Inches (taille de la marge extérieure en pouces). Voici cette liste triée par ordre alphabétique du nom des paramètres avec la ou les valeurs par défaut lorsqu'elles existent.
Paramètre Longueur Valeur
[1,] adj 1 0.5
[2,] ann 1 TRUE
[3,] ask 1 FALSE
[4,] bg 1 white
[5,] bty 1 o
[6,] cex 1 1
[7,] cex.axis 1 1
[8,] cex.lab 1 1
[9,] cex.main 1 1.20000004768372
[10,] cex.sub 1 1
[11,] cin 2 0.15 0.2
[12,] col 1 black
[13,] col.axis 1 black
[14,] col.lab 1 black
[15,] col.main 1 black
[16,] col.sub 1 black
[17,] cra 2 10.8 14.4
[18,] crt 1 0
[19,] csi 1 0.2
[20,] cxy 2 0.01 0.02
[21,] din 2 14 12.26
[22,] err 1 0
[23,] family 1 <<vide>>
[24,] fg 1 black
[25,] fig 4 0 1 0 1
[26,] fin 2 14 12.26
[27,] font 1 1
[28,] font.axis 1 1
[29,] font.lab 1 1
[30,] font.main 1 2
[31,] font.sub 1 1
[32,] lab 3 5 5 7
[33,] las 1 0
[34,] lend 1 round
[35,] lheight 1 1
[36,] ljoin 1 round
[37,] lmitre 1 10
[38,] lty 1 solid
[39,] lwd 1 1
[40,] mai 4 1.02 0.82 0.82 0.42
[41,] mar 4 5.1 4.1 4.1 2.1
[42,] mex 1 1
[43,] mfcol 2 1 1
[44,] mfg 4 1 1 1 1
[45,] mfrow 2 1 1
[46,] mgp 3 3 1 0
[47,] mkh 1 0.001
[48,] new 1 FALSE
[49,] oma 4 0 0 0 0
[50,] omd 4 0 1 0 1
[51,] omi 4 0 0 0 0
[52,] pch 1 1
[53,] pin 2 12.76 10.42
[54,] plt 4 0.06 0.97 0.08 0.93
[55,] ps 1 12
[56,] pty 1 m
[57,] smo 1 1
[58,] srt 1 0
[59,] tck 1 <<NA>>
[60,] tcl 1 -0.5
[61,] usr 4 0 1 0 1
[62,] xaxp 3 0 1 5
[63,] xaxs 1 r
[64,] xaxt 1 s
[65,] xlog 1 FALSE
[66,] xpd 1 FALSE
[67,] yaxp 3 0 1 5
[68,] yaxs 1 r
[69,] yaxt 1 s
[70,] ylbias 1 0.1
[71,] ylog 1 FALSE
Contrairement aux fonctions statistiques, les fonctions graphiques fournies par R sont difficiles à maitriser compte-tenu des nombreux paramètres mis en jeu. De plus des packages complémentaires comme lattice avec 148 objets et ggplot2 avec 240 objets fournissent des fonctions complémentaires parfois encore plus techniques. Il est d'usage de progresser prudemment et de ne pas chercher tout de suite à tout réaliser dans un graphique avec R mais au contraire de "monter" progressivement les graphiques. Une fois le tracé obtenu, la programmation permet d'automatiser la production de graphiques avec le même "profil".
Pour sauvegarder les paramètres graphiques courants, il suffit de stocker le résultat de la fonction par(). On peut ensuite réaffecter l'objet sauvegardé. En voici un exemple :
# des données fournies par R
data(trees)
with(trees, plot(Height,Volume,main="Arbres") ) # le titre est en noir
sovParg <- par() # sauvegarde des paramètres
par(col.main="red") # désormais les titres de tracé sont en rouge
with(trees, plot(Height,Volume,main="Arbres") ) # le titre est en rouge
# on remet les paramètres sauvegardés
par( sovParg )
Le package ggplot2 implémente la grammaire des graphiques au sens de L. Wilkinson. Une carte de référence en français est ici.
Le package lattice contient également des fonctions intéressantes pour des graphiques par groupe, par série. Un livre chez Springer lui est consacré.
2. Quelles instructions pour quels tracés ?
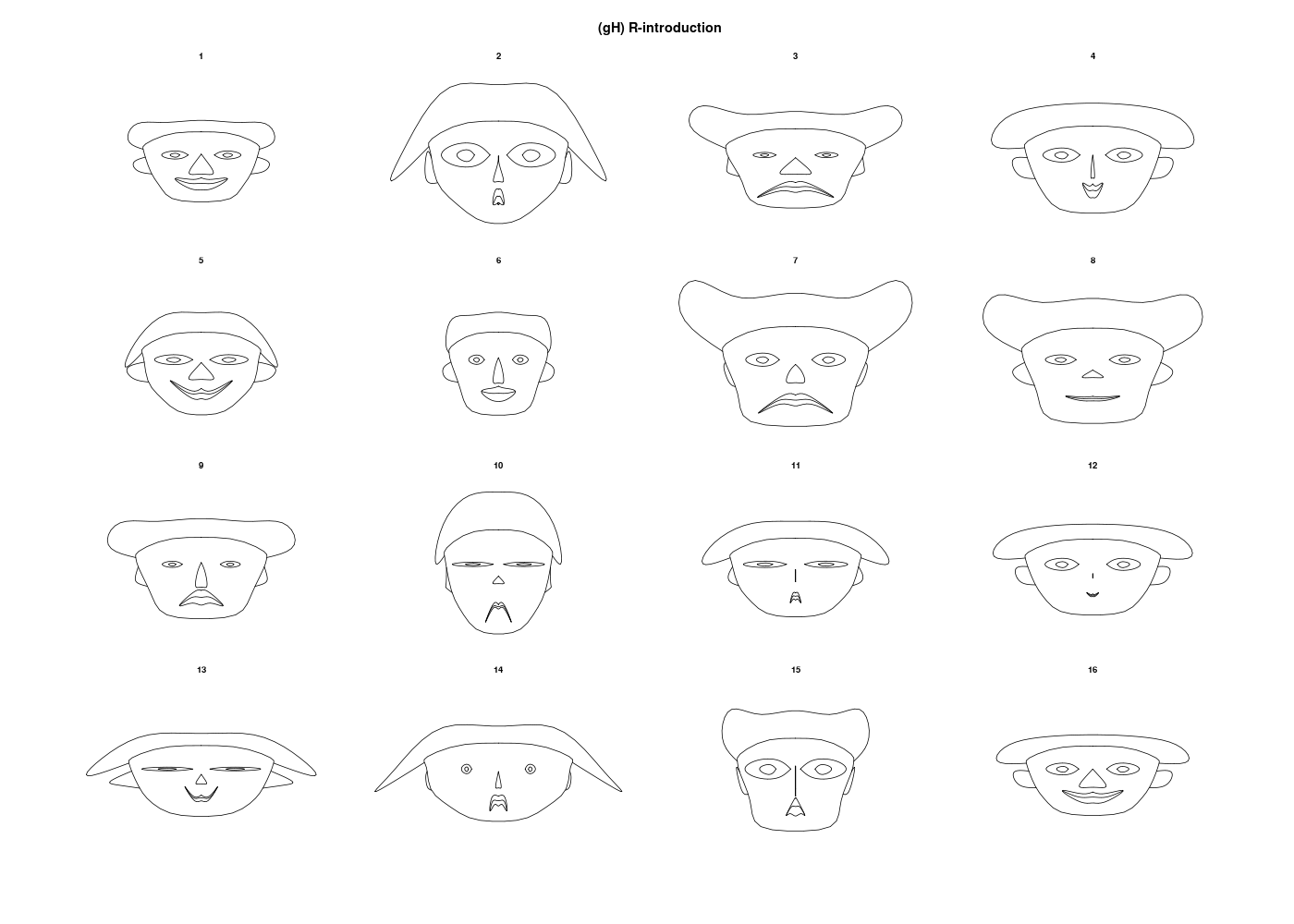
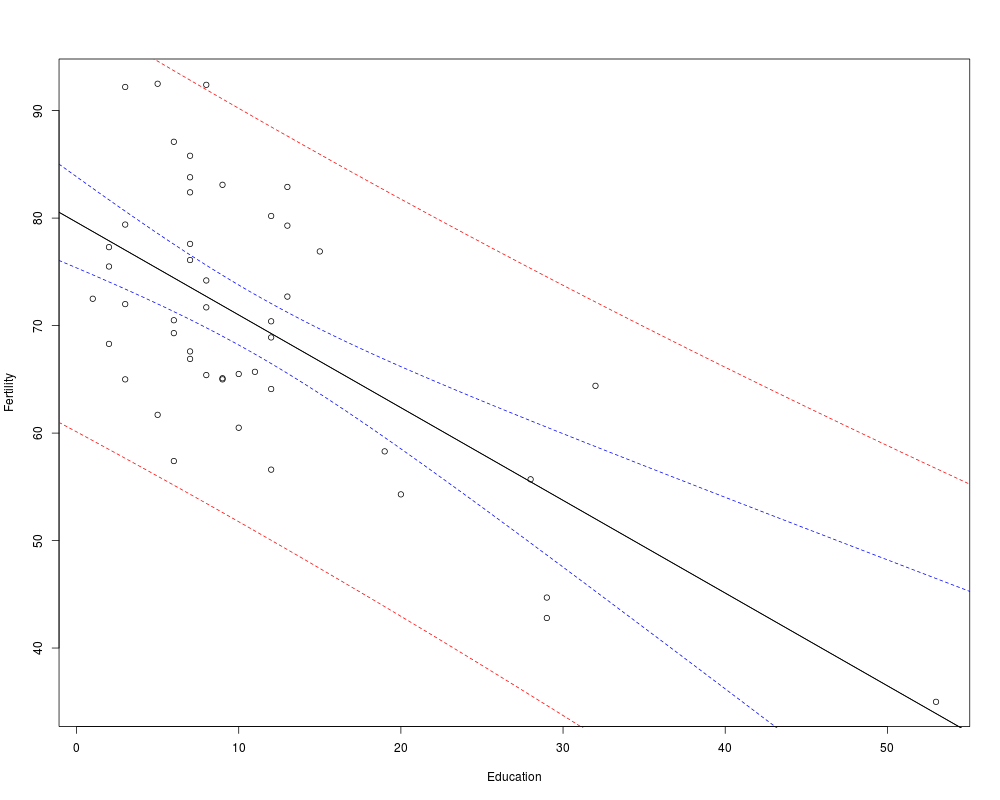
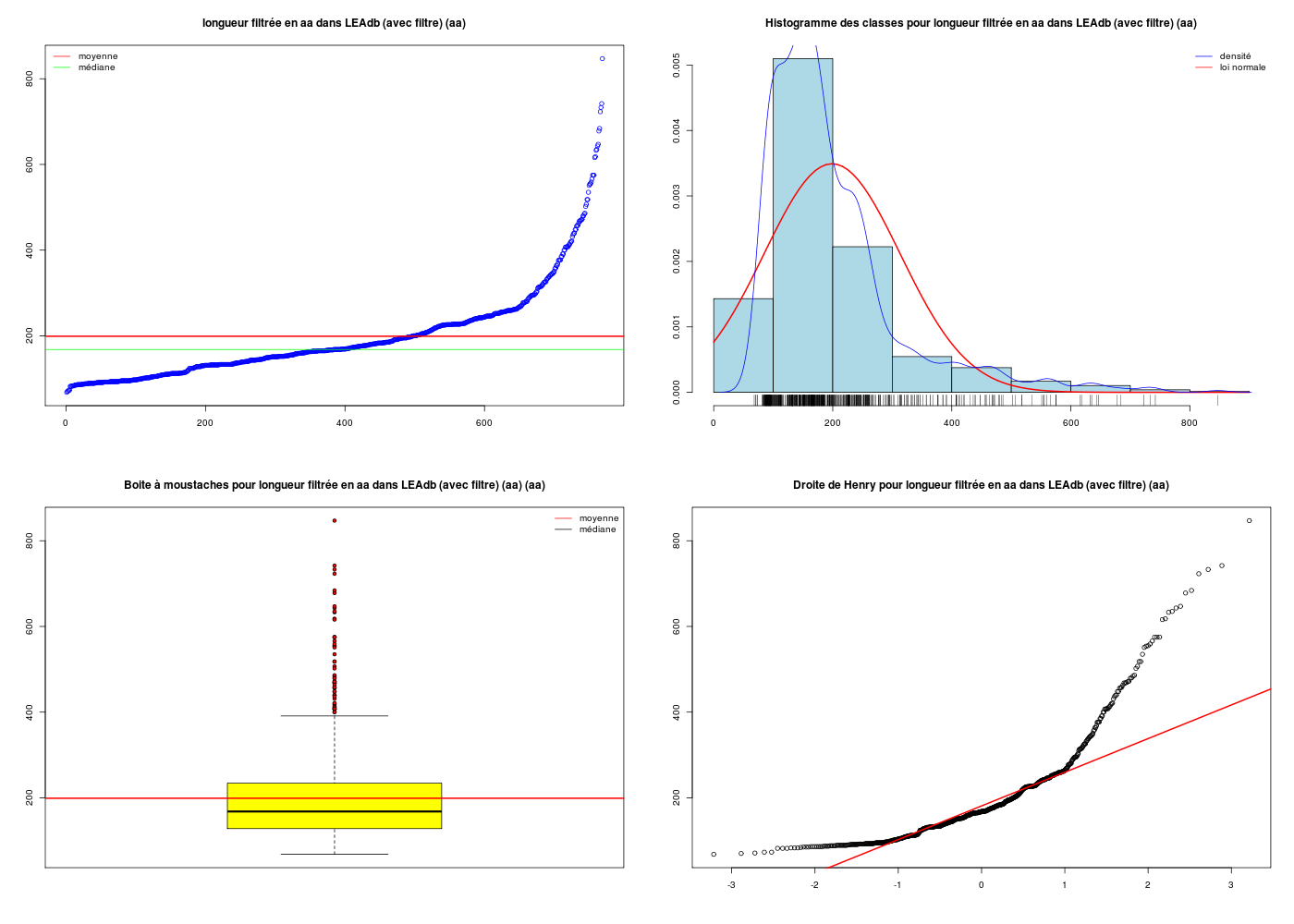
Combien d'instructions R faut-il pour réaliser le graphique suivant, si les données sont dans la variable lng ? Et avec les fonctions (gH) ?
On pourra par exemple lire les données de longueur, issues du dossier LEADB avec les instructions suivantes :
source("http://www.info.univ-angers.fr/~gh/statgh.r",encoding="latin1")
lea <- lit.dar("http://www.info.univ-angers.fr/~gh/Datasets/lea.dar")
lng <- lea$length
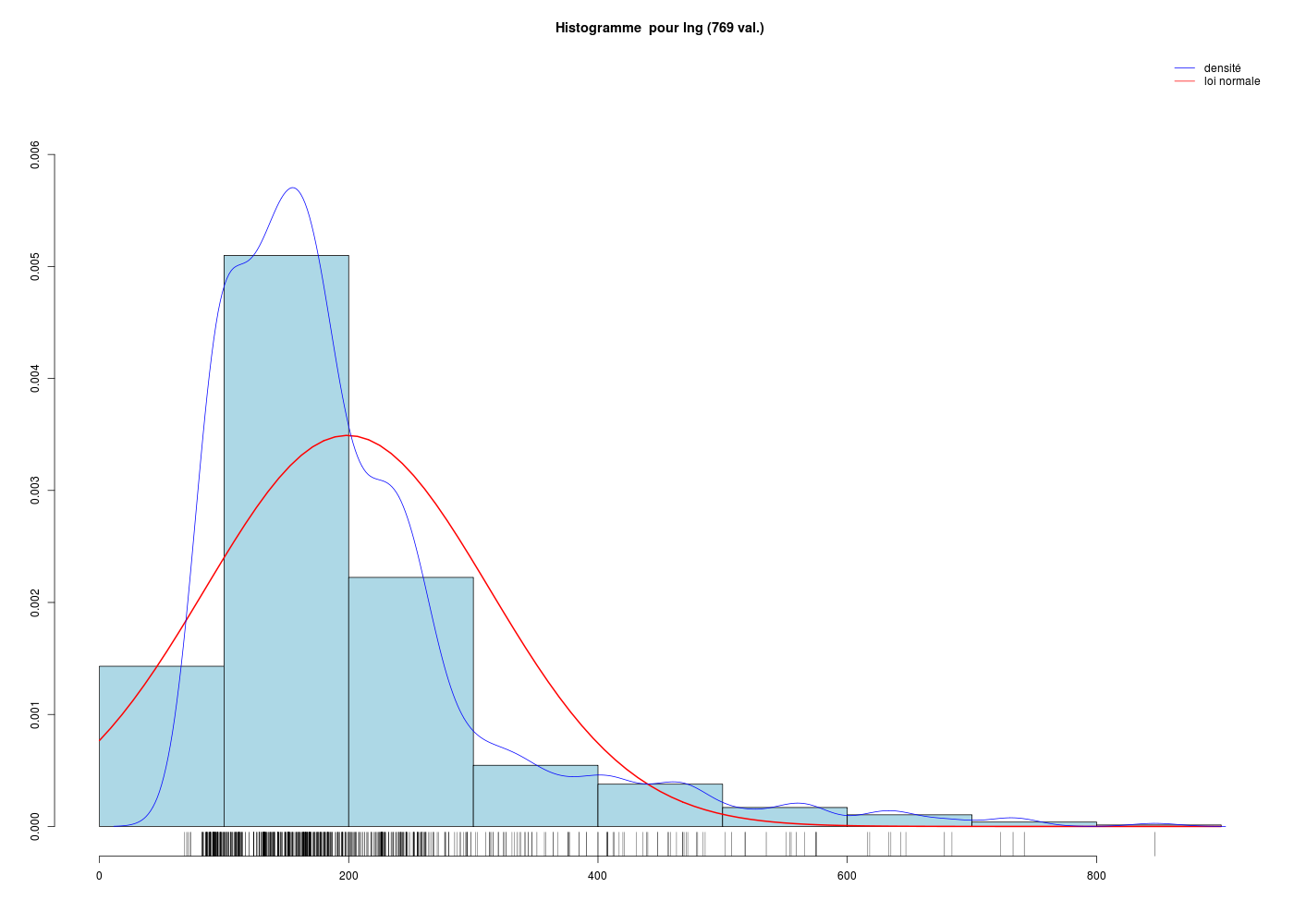
Il y a visiblement
-
un histogramme en bleu ciel, tracé via la fonction hist(),
-
la loi normale en rouge, sans doute tracée via curve(),
-
la courbe de densité estimée par noyau en bleu foncé via lines(),
-
une estimation visuelle de la densité via un "peigne" sur l'axe x avec rug(),
-
une légende en haut et à droite obtenue par legend(),
-
et enfin un titre et les labels pour les axes produits par title().
Il faut donc sans doute six instructions de tracé pour réaliser le graphique. Vérification (tester par copier/coller de chaque ligne au fur et à mesure) :
# lecture des données
source("http://www.info.univ-angers.fr/~gh/statgh.r",encoding="latin1")
lea <- lit.dar("http://www.info.univ-angers.fr/~gh/Datasets/lea.dar")
lng <- lea$length
# histogramme (adapté sur l'axe Y pour la densité)
hist(lng,col="lightblue",main="",probability=TRUE,ylim=c(0,0.006),xlab="",ylab="")
# loi normale associée et son tracé
vnorm <- function(x) { return( dnorm(x,mean=mean(lng),sd=sd(lng)) ) }
curve(vnorm,add=TRUE,col="red",lwd=2)
# densité estimée par noyau et son tracé
dns <- density(lng)
lines(dns,col="blue")
# "peigne" de densité sur l'axe X
rug(lng)
# la légende en haut et à droite
legend(x="topright",c("densité","loi normale"),col=c("blue","red"),lty=c(1,1),bty="y")
# le titre et les labels des axes
titre <- paste("Histogramme des",length(lng),"longueurs")
title(main=titre,xlab="longueur des séquences",ylab="densité")
Les fonctions dnorm() et density() font partie du package stats, bien sûr.
Avec les fonctions gH, une seule instruction suffit, qui fournit aussi l'analyse statistique de la variable et trois autres graphiques, nommée decritQT :
decritQT("Longueurs LEAdb",lng,"aa",TRUE)
##########################################################
#
# en mode long :
#
##########################################################
decritQT(
titreQT="Longueurs LEAdb",
nomVar=lng,
unite="aa",
lng="FR",
graphique=TRUE
) # fin de decritQT
DESCRIPTION STATISTIQUE DE LA VARIABLE Longeurs LEAdb
Taille 773 individus
Moyenne 205.6882 aa
Ecart-type 148.5962 aa
Coef. de variation 72 %
1er Quartile 130.0000 aa
Mediane 168.0000 aa
3eme Quartile 236.0000 aa
iqr absolu 106.0000 aa
iqr relatif 63.0000 %
Minimum 68 aa
Maximum 1864 aa
Tracé tige et feuilles
The decimal point is 2 digit(s) to the right of the |
0 | 777778888888999999999999999999999999999999999999999999999999999999999999999999
1 | 0000000000000000000000000000000000000000000000011111111111111111111111111111111111111111111122222222222223333333333333+273
2 | 0000000000000000000000000000111111111111111122222222222222333333333333333333333333333333333333333444444444444444444444+57
3 | 000000011111222223333344444445556666788889999
4 | 0011111112223444556666777778889
5 | 0122455667888
6 | 22344588
7 | 234
8 | 5
9 |
10 |
11 |
12 | 4
13 |
14 | 3
15 | 1
16 |
17 |
18 | 6
S'il semble très facile de tracer des histogrammes, des courbes de densité, les calculs et les choix (nombre de classes, valeur de la densité...) font appel à des connaissances statistiques avancées. Voir par exemple la page density estimation, sans doute plus intéressante que la page estimation par noyau dont une application intéressante est en géographie humaine ici.
3. Tracé de points, de courbes et gestion des options (axes, couleurs...)
Comment tracer deux séries de points l'une en fonction de l'autre ? Et avec une couleur différente selon un troisième critère ?
Comment retrouver les différents symboles utilisables pour plot() ? Et comment ajouter une légende ?
On pourra par exemple tracer le poids en fonction de la taille pour les données HER avec une seule couleur (noir) puis tracer avec les hommes en bleu et les femmes en rouge.
Le tracé de points et de lignes peut se faire avec plot(), points() et lines(). Pour l'instant nous ne présenterons que plot() du package graphics.
La syntaxe de base de plot() est plot(x,y), mais on peut aussi utiliser la syntaxe plot(y~x) où le symbole ~ (tilde) se lit «en fonction de ». Le paramètre type permet de choisir entre points, lignes ou les deux, etc. Le paramètre main correspond au titre (principal). Le paramètre col choisit la couleur de tracé. Voici donc quelques exemples à copier/coller.
library(datasets)
data(trees) # les variables Volume et Height sont donc définies
idx <- order(trees$Height)
arbres <- cbind(trees$Height[idx],trees$Volume[idx])
plot(arbres[,1],arbres[,2],main="des arbres") # équivalent à plot(x=arbres[,1],y=arbres[,2])
plot(arbres,main="des arbres (2)",col.main="blue") # même tracé, car arbres n'a que deux colonnes
# avec des variables, c'est plus lisible qu'avec des indices
hautr <- arbres[,1]
volum <- arbres[,2]
plot(hautr,volum) # équivalent à plot(x=hautr,y=volum) et sans titre
plot(volum~hautr,main="pareil") # même tracé, ~ se lit "en fonction de "
plot(x=hautr,y=volum,main="des points",type="p")
plot(x=hautr,y=volum,main="des lignes",type="l")
plot(x=hautr,y=volum,main="les deux, mon capitaine !",type="b",cex=2,col="blue")
# un tracé plus sophistiqué
plot(
x=hautr,y=volum,type="b",cex=1.5,col="blue",pch=21,bg="yellow",fg="red",
main="ARBRES",sub="(données issues de datasets)",
xlab="hauteur en cm",ylab="volume en cm**3"
) # fin de plot
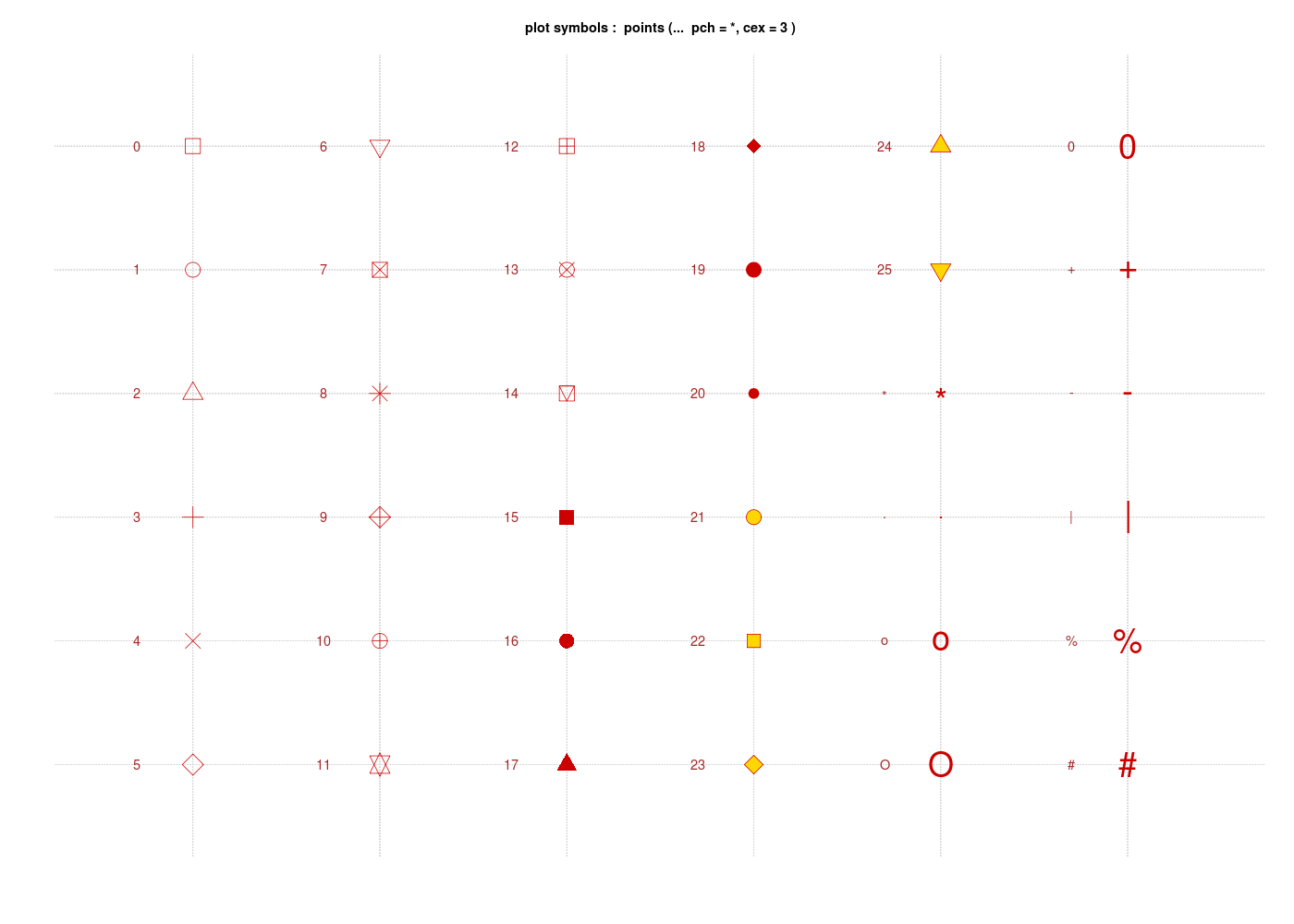
Les différents caractères possibles à utiliser (pch=Plot CHaracter) sont affichés si on tape example(pch). En voici une partie :
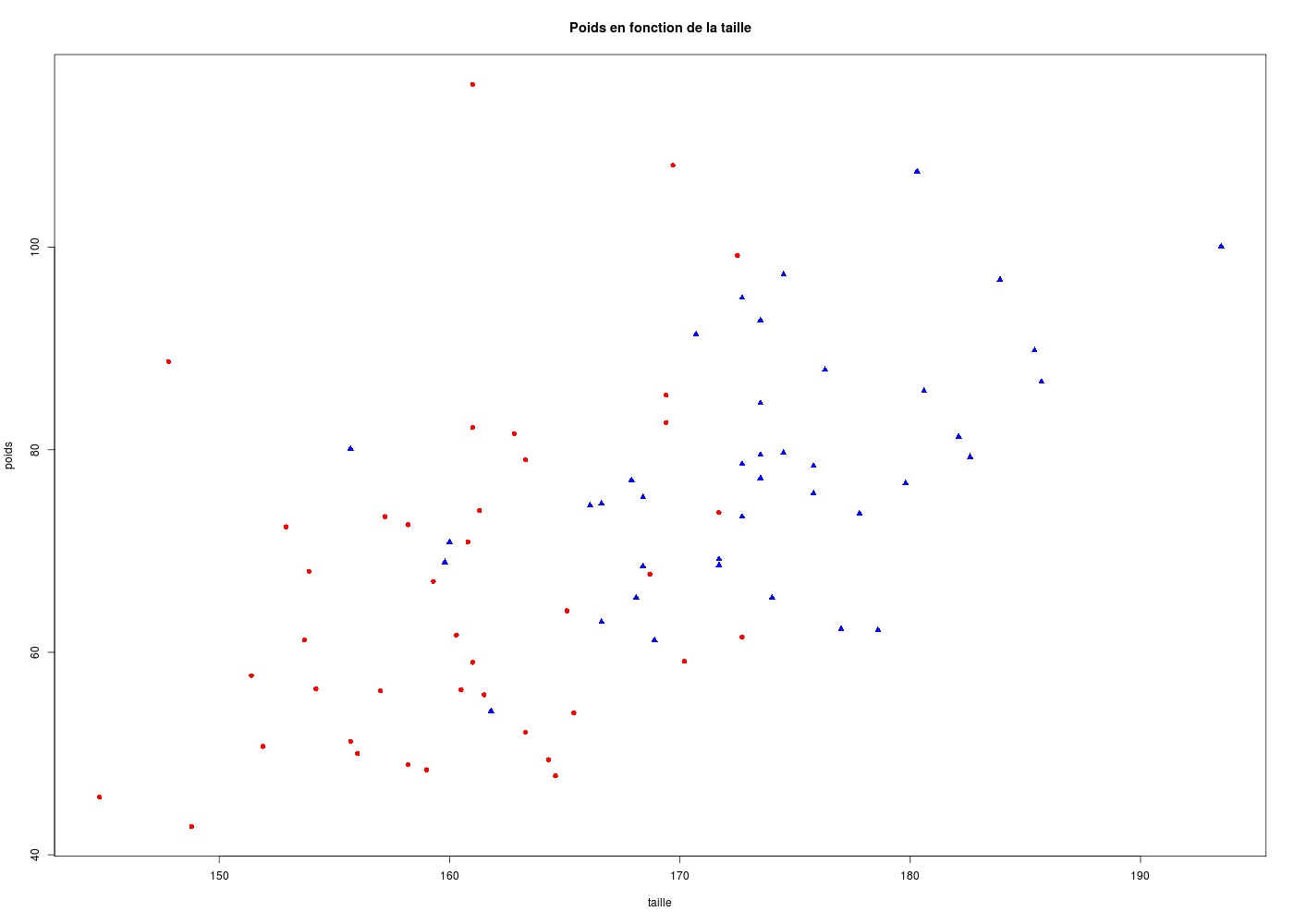
Pour les données HER, nous allons utiliser un triangle bleu, pointe en haut, pour les hommes soit pch=17 et col="blue" alors que nous prendrons un rond rouge pour les femmes, soit pch=16 et col="red". On utilise la variable SEXE pour générer les filtres correspondants :
## fichier her1.r
# lecture des fonctions (gH)
source("http://www.info.univ-angers.fr/~gh/statgh.r",encoding="latin1")
# lecture des données avec une fonction (gH)
her <- lit.dar("http://www.info.univ-angers.fr/~gh/Datasets/her.dar")
attach(her) # évite de répéter her$... devant le nom des variables
couleurs <- c("blue","red") # codage 0=Homme, 1=Femme
caracteres <- c(17,16) # donc code des hommes avant celui des femmes
# comme sexe est en 0,1 on ajoute 1 pour en faire des indices
coulHER <- couleurs[ 1 + sexe ]
carsHER <- caracteres[ 1 + sexe ]
# décommenter la ligne qui suit pour produire le fichier PNG
# png(filename="her1.png",width=1400,height=1000)
plot(poids~taille,col=coulHER,pch=carsHER,main="Poids en fonction de la taille")
# décommenter la ligne qui suit en cas de production de fichier PNG
# dev.off()
# une autre façon de faire est de passer par ifelse
coulHER <- ifelse(sexe==0,"blue","red")
carsHER <- ifelse(sexe==0,17,16)
# décommenter la ligne qui suit pour produire le fichier PNG
#png(filename="her2.png",width=1400,height=1000)
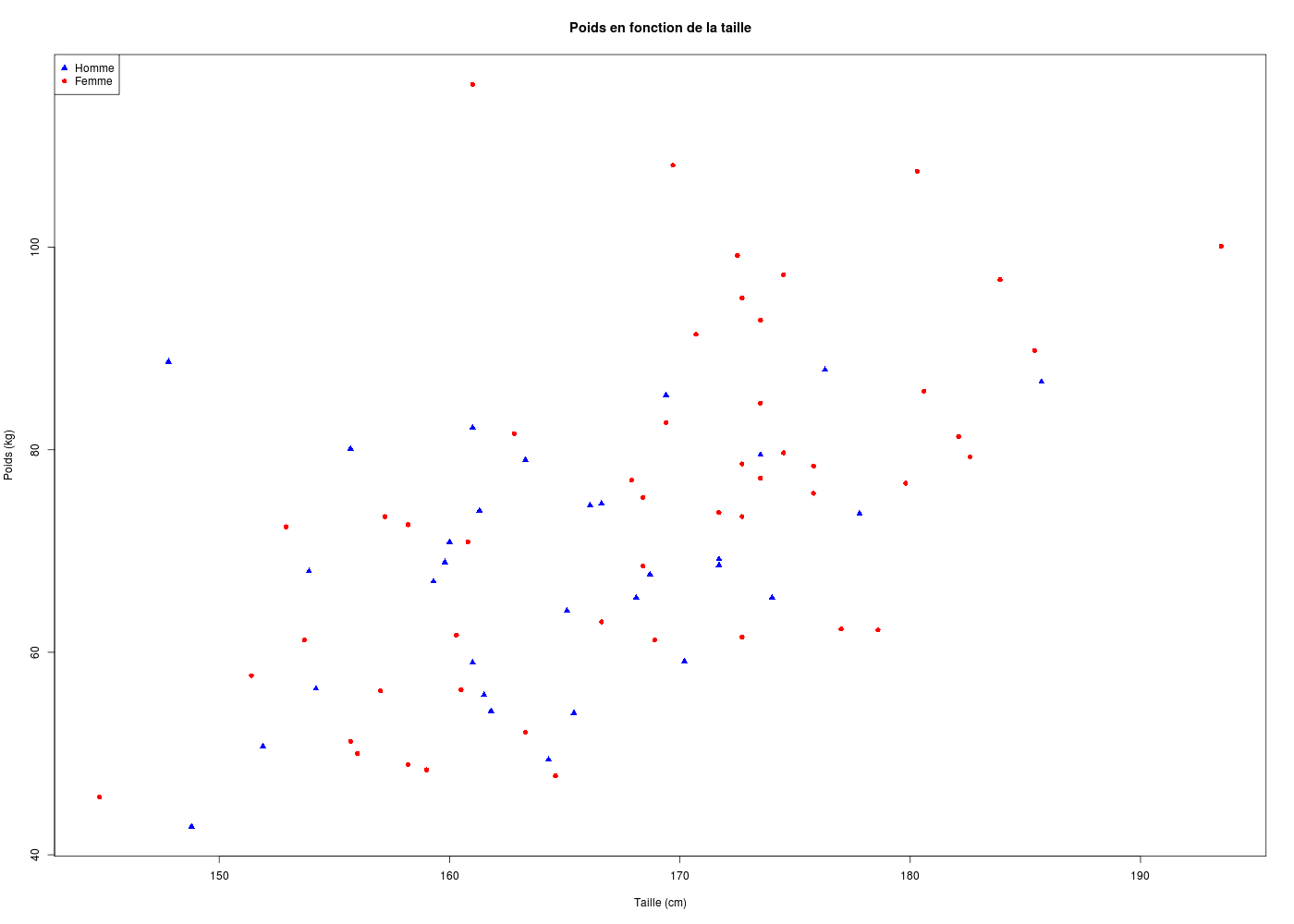
plot(poids~taille,col=coulHER,pch=carsHER,main="Poids en fonction de la taille",xlab="",ylab="")
title(xlab="Taille (cm)",ylab="Poids (kg)")
legend(x="topleft",legend=c("Homme","Femme"),col=c("blue","red"),pch=17:16)
# décommenter la ligne qui suit en cas de production de fichier PNG
#dev.off()
# à ne pas oublier, sous peine de voir apparaitre le le message d'erreur
#
# << Les objets suivants sont masqués from her (position 3):
#
# age, bras, chol, coud, dia, imc, jmbg, poids, poign, pouls, sexe, sys, taille, ttaille
# >>
detach(her)
La fonction title() gère le titre (main), le sous-titre (sub) et les labels des axes (xlab et ylab) alors que la fonction legend() permet d'expliciter les symboles, caractères et couleurs utilisés. La fonction png() redirige la sortie graphique vers un fichier PNG et la fonction dev.off() permet de fermer le fichier image généré.
4. Superposition de graphiques
Est-ce simple d'ajouter des points à un graphique en R ? Et de rajouter des lignes ? Et de quadriller le graphique ? On pourra, par exemple, pour les variables poids et tailles précédentes, ajouter des lignes pour les moyennes, les points médians...
On voudrait superposer plusieurs tracés de plot(), par exemple la colonne Y en fonction de X, puis la colonne Z en fonction de X sur le même graphique. Comment réaliser cela en R ? Et produire deux graphiques (ou plus) dans une même fenêtre ? On utilisera les prix par année du dossier LOGEMENT pour tester ces graphiques.
La fonction points() permet d'ajouter des points à un graphique alors que la fonction abline() permet d'ajouter une droite. La fonction rect() trace un rectangle. Si on utilise plot(...,type="n") R ne trace rien mais définit le cadre graphique. On peut alors tracer à nouveau avec plot() à condition d'utiliser par(new=TRUE) avant lorsqu'on veut superposer des graphiques. C'est ce que nous avons fait ci-dessous, avec un appel à grid() pour ajouter un quadrillage.
## Attention, ceci est la suite de her1.r qui contient la lecture des données
# décommenter la ligne qui suit pour produire le fichier PNG
# png(filename="her3.png",width=1400,height=1000)
plot(poids~taille,type="n",main="",xlab="",ylab="")
rect(xleft=min(taille),ybottom=min(poids),xright=max(taille),ytop=max(poids),col="lightyellow")
par(new=TRUE)
plot(poids~taille,col=coulHER,pch=carsHER,main="Poids en fonction de la taille",xlab="",ylab="")
title(xlab="Taille (cm)",ylab="Poids (kg)")
legend(x="topleft",legend=c("Homme","Femme"),col=c("blue","red"),pch=17:16)
# une grille en pointillés
grid(15,10,lty=2,lwd=2,col="lightgreen")
# la légende du bas pour les droites
legend(
x="bottomright",
legend=c("Poids moyen Homme","Poids moyen Femme","Régression globale"),
col=c("blue","red","black"),bty="n",lwd=2
) # fin de legend
# poids moyen des hommes
abline(h=mean(poids[sexe==0]),col="blue")
# poids moyen des femmes
abline(h=mean(poids[sexe==1]),col="red")
# droite de régression globale
abline(lm(poids~taille),lwd=2)
# décommenter la ligne qui suit en cas de production de fichier PNG
# dev.off()
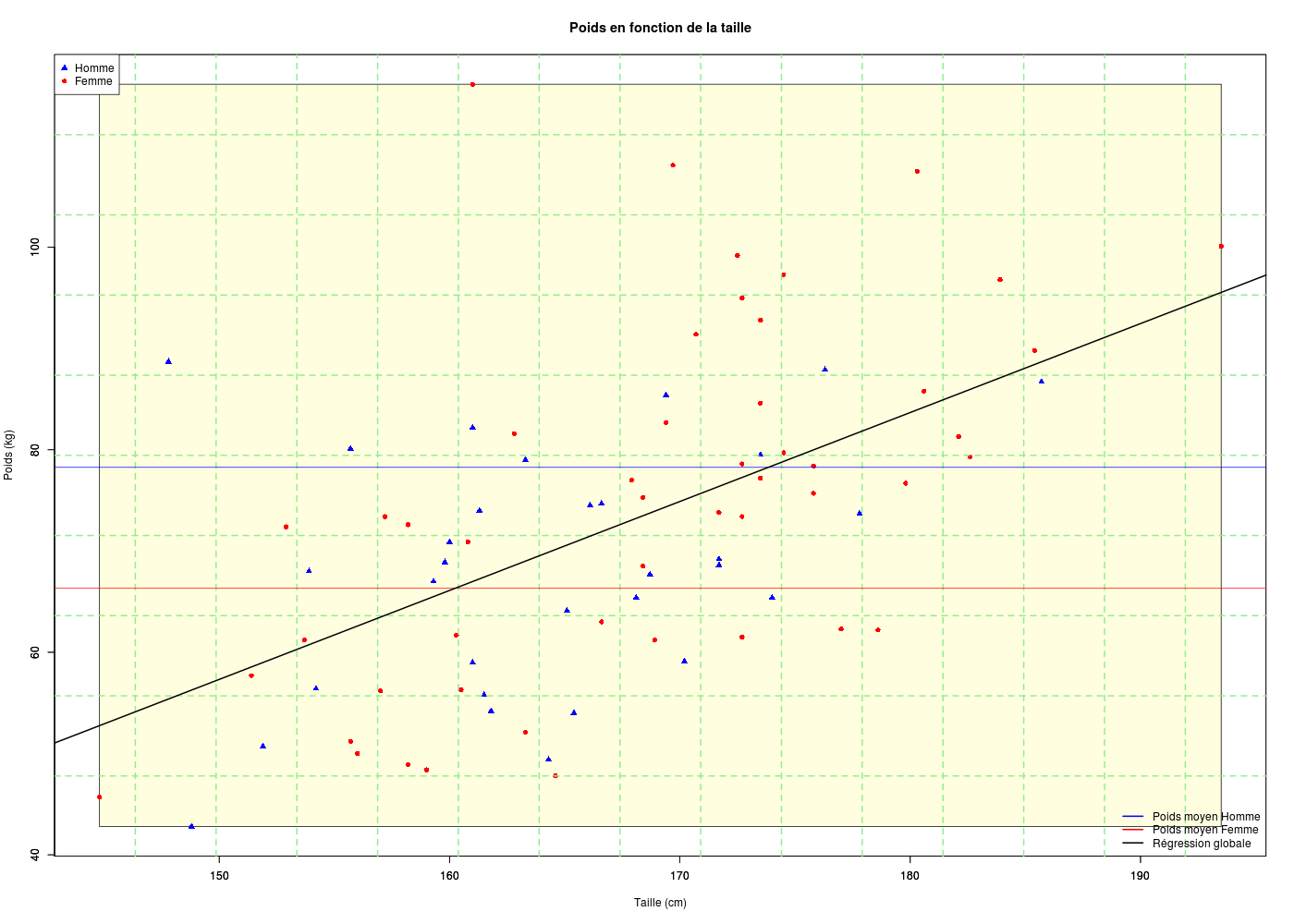
Avec text() on peut écrire ce qu'on veut dans le graphique. arrows() permet d'ajouter des flèches. Comme le symbole ♀ n'est pas disponible directement en R, nous avons été le chercher dans le package TeachingDemos via my.symbols() et ms.female. Enfin, pour écrire dans la marge, nous avons utilisé mtext() après avoir modifié les paramètres graphiques omi (Outer margin in Inches) et mai (MArgin size in Inches). On pourra consulter la page mar-oma pour mieux comprendre ces paramètres graphiques et ceux qui sont associés comme oma (Outer MArgin in lines) et mar (MARgin size in lines).
# Attention, ceci est aussi la suite de her1.r qui contient la lecture des données
library(TeachingDemos) # pour la fonction my.symbols()
# décommenter la ligne qui suit pour produire le fichier PNG
png(filename="her4.png",width=1400,height=1000) # avant par()...
sovpg <- par()
newOmi <- par()$omi
newOmi[4] <- 1
par(omi=newOmi)
newMai <- par()$mai
newMai[4] <- 1.
par(mai=newMai)
plot(poids~taille,col=coulHER,pch=carsHER,main="Poids en fonction de la taille",xlab="",ylab="")
title(xlab="Taille (cm)",ylab="Poids (kg)")
legend(x="topleft",legend=c("Homme","Femme"),col=c("blue","red"),pch=17:16)
# une grille en pointillés
grid(15,10,lty=2,lwd=2,col="lightgreen")
# la légende
legend(
x="bottomright",
legend=c("Moyennes Homme","Moyennes Femme","Régression globale"),
col=c("blue","red","black"),bty="n",lwd=2
) # fin de legend
# moyennes hommes
abline(h=mean(poids[sexe==0]),col="blue")
abline(v=mean(taille[sexe==0]),col="blue")
# moyennes des femmes
abline(h=mean(poids[sexe==1]),col="red")
abline(v=mean(taille[sexe==1]),col="red")
# droite de régression globale
abline(lm(poids~taille),lwd=2)
# homme médian
points(x=median(taille[sexe==0]),y=median(poids[sexe==0]),pch=19,col="black",cex=1.5)
text(x=median(taille[sexe==0])+3,y=median(poids[sexe==0]),labels="Homme médian",cex=0.8)
# femme médiane
points(x=median(taille[sexe==1]),y=median(poids[sexe==1]),pch=19,col="black",cex=1.5)
text(x=median(taille[sexe==1])+3,y=median(poids[sexe==1]),labels="Femme médiane",cex=0.9)
# flèche sur poids extreme (femme)
mf <- max(poids[sexe==1])
xf <- taille[sexe==1][which.max(poids[sexe==1])] # attention !
arrows(x0=xf+5,y0=mf,x1=xf+1,y1=mf,lwd=3,col="orange")
my.symbols(xf+6,mf, ms.female, add=TRUE, inches=0.4,col=c('darkgreen'),cex=2,lwd=3 )
# un texte dans la marge
mtext(text="Données HER (Triola)",side=4,col="darkblue",cex=2,outer=TRUE)
# décommenter la ligne qui suit en cas de production de fichier PNG
dev.off()
print( par()$omi )
par(sovpg)
print( par()$omi )
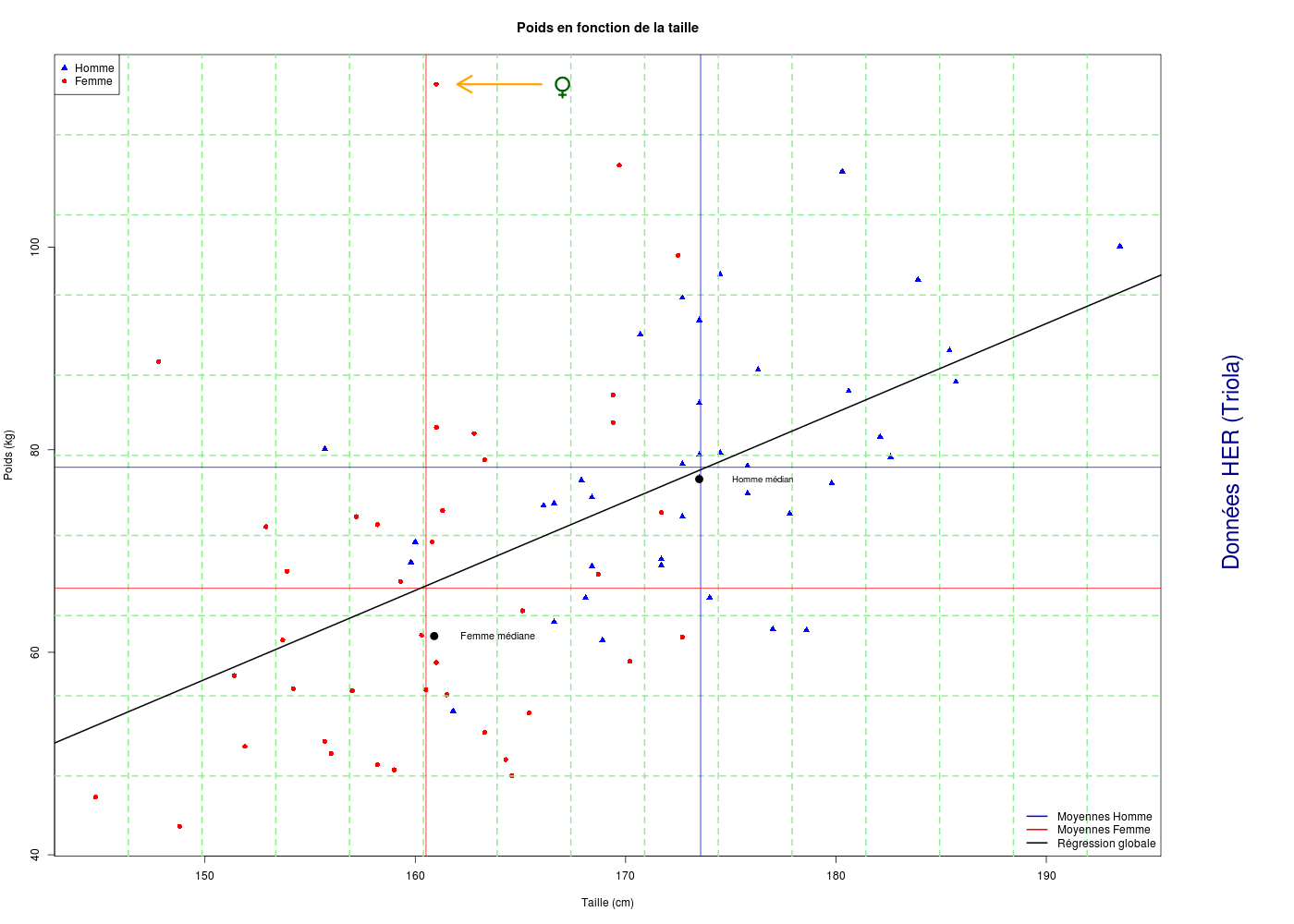
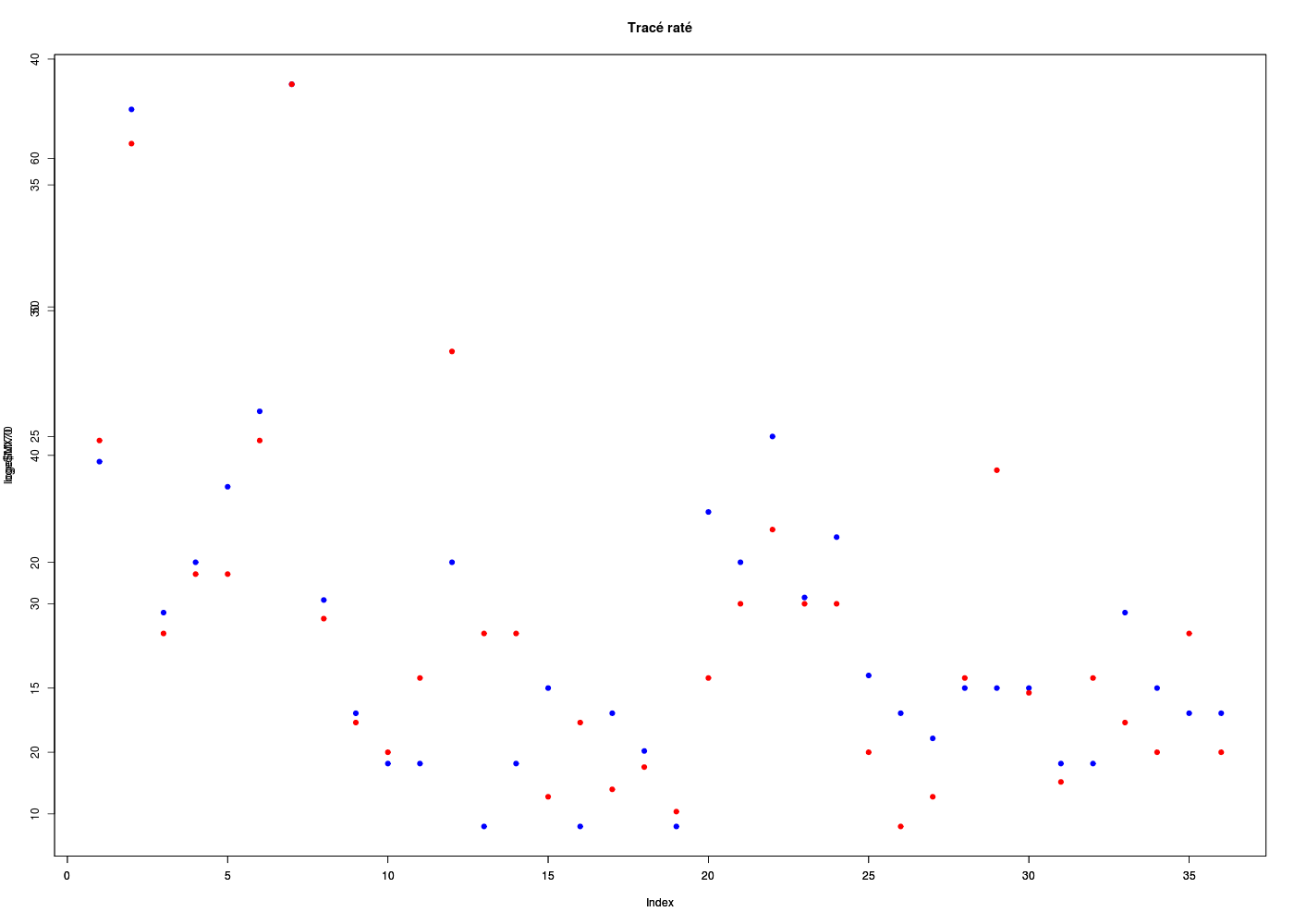
Pour afficher deux tracés sur un même graphique, «bricoler» avec plot() et ses options aboutit souvent à un graphique raté (superposition des axes, des titres...) même avec par(new=TRUE) :
# lecture des fonctions (gH)
source("http://www.info.univ-angers.fr/~gh/statgh.r",encoding="latin1")
# lecture des données avec une fonction (gH)
loge <- lit.dar("http://www.info.univ-angers.fr/~gh/Datasets/logement.dar")
# essai (raté) des tracés de min et max pour 1970
plot(loge$MI70,col="blue",pch=19,main="Tracé raté")
par(new=TRUE) # comme si c'était un nouveau tracé
plot(loge$MX70,col="red",pch=19)
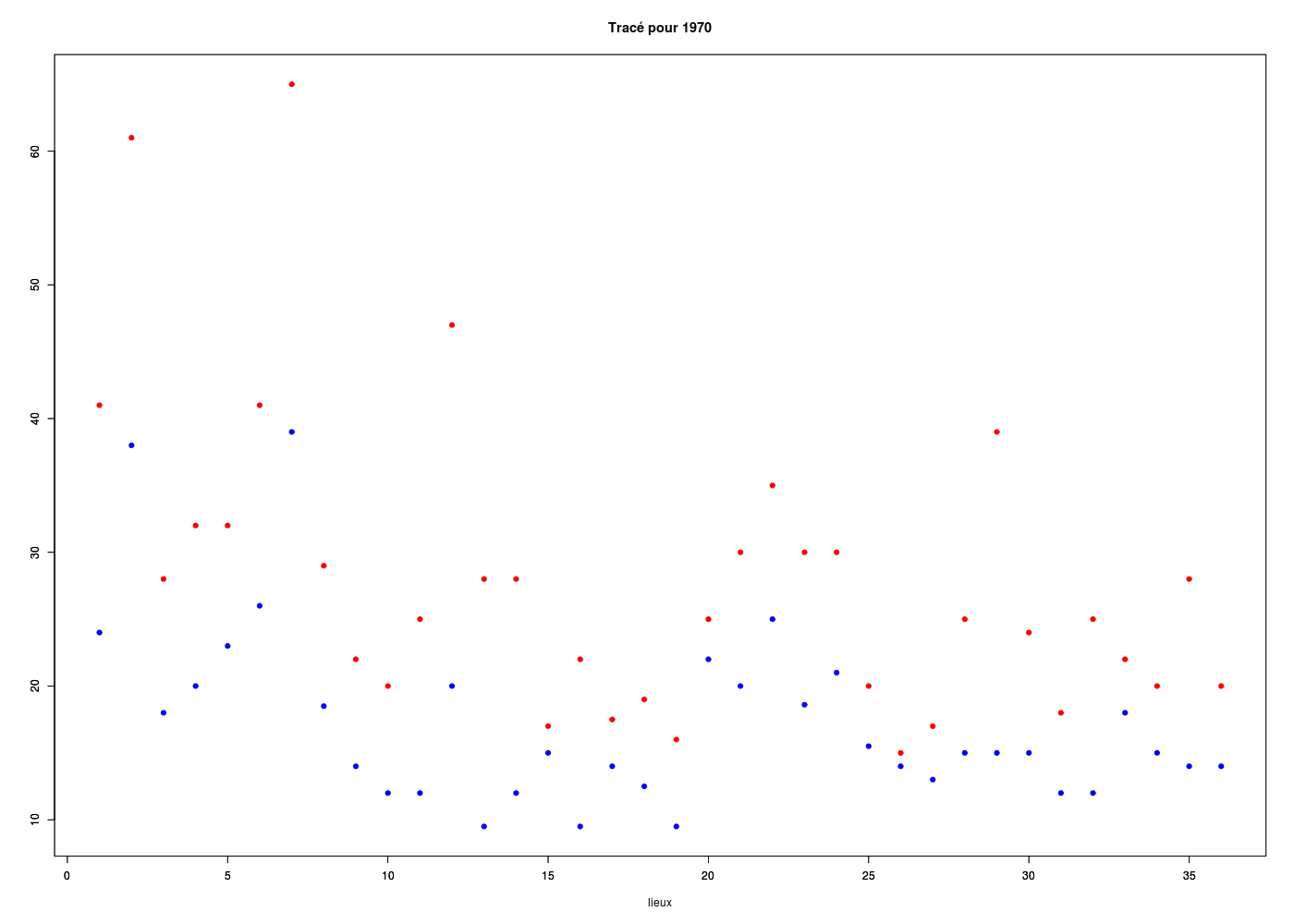
Ou alors, il faut prendre beaucoup de précautions :
# lecture des fonctions (gH)
source("http://www.info.univ-angers.fr/~gh/statgh.r",encoding="latin1")
# lecture des données avec une fonction (gH)
loge <- lit.dar("http://www.info.univ-angers.fr/~gh/Datasets/logement.dar")
# une solution un peu "lourdingue"
ymin <- min(c(loge$MI70,loge$MX70))
ymax <- max(c(loge$MI70,loge$MX70))
plot(loge$MI70,col="blue",pch=19,main="Tracé pour 1970",xlab="lieux",ylab="",ylim=c(ymin,ymax))
par(new=TRUE) # comme si c'était un nouveau tracé
plot(loge$MX70,col="red",pch=19,main="",xlab="",ylab="",ylim=c(ymin,ymax))
Il est d'usage, lorsqu'on veut effectuer plusieurs tracés sur une même zone graphique avec un même axe X, de déterminer le maximum global en Y, d'effectuer le premier tracé avec plot() et les tracés suivants avec points() ou lines().
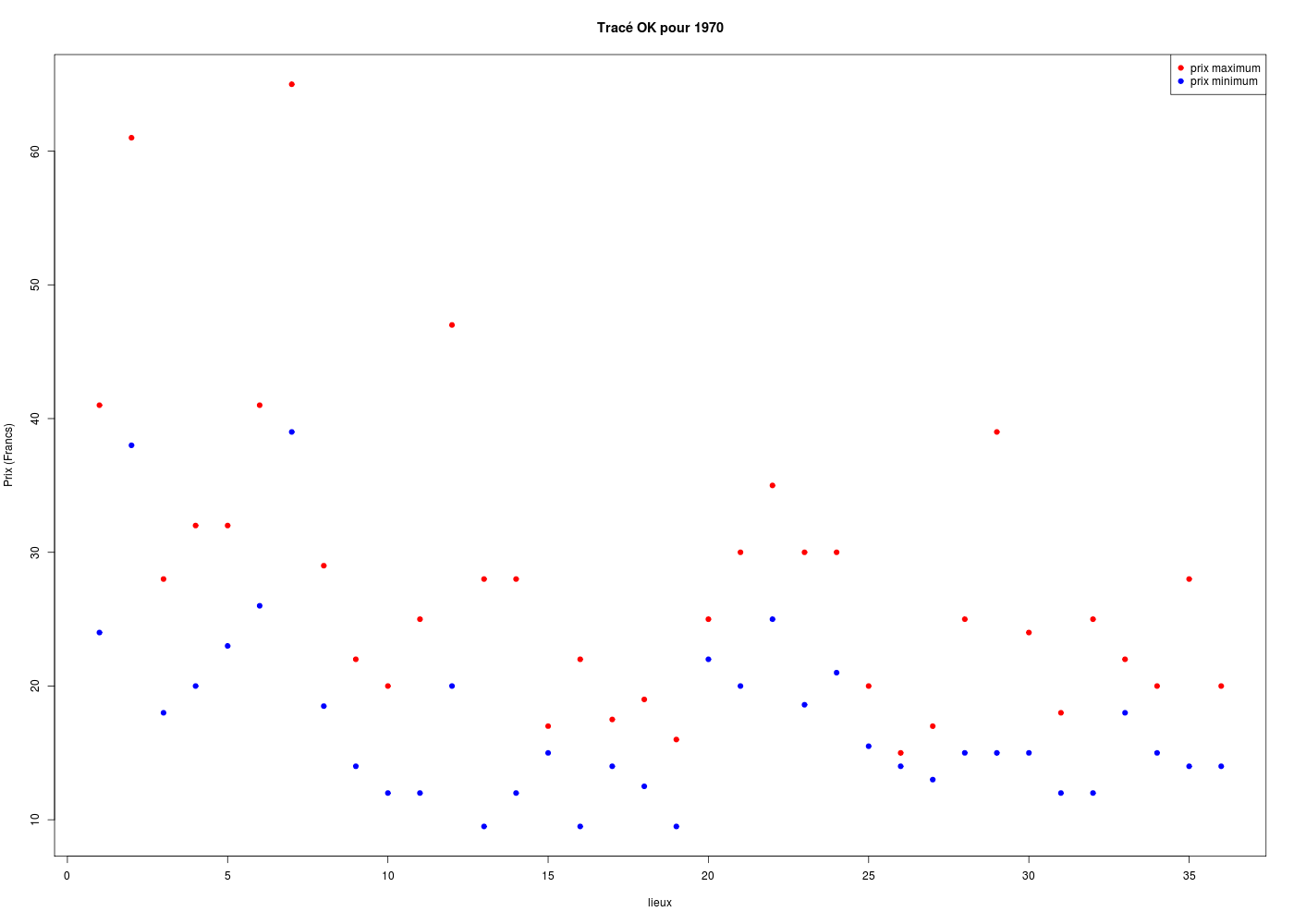
# lecture des fonctions (gH)
source("http://www.info.univ-angers.fr/~gh/statgh.r",encoding="latin1")
# lecture des données avec une fonction (gH)
loge <- lit.dar("http://www.info.univ-angers.fr/~gh/Datasets/logement.dar")
# la solution classique
ymin <- min(c(loge$MI70,loge$MX70))
ymax <- max(c(loge$MI70,loge$MX70))
plot(loge$MI70,col="blue",pch=19,main="Tracé OK pour 1970",xlab="lieux",ylab="Prix (Francs)",ylim=c(ymin,ymax))
points(loge$MX70,col="red",pch=19)
legend(x="topright",legend=c("prix maximum","prix minimum"),col=c("red","blue"),pch=19)
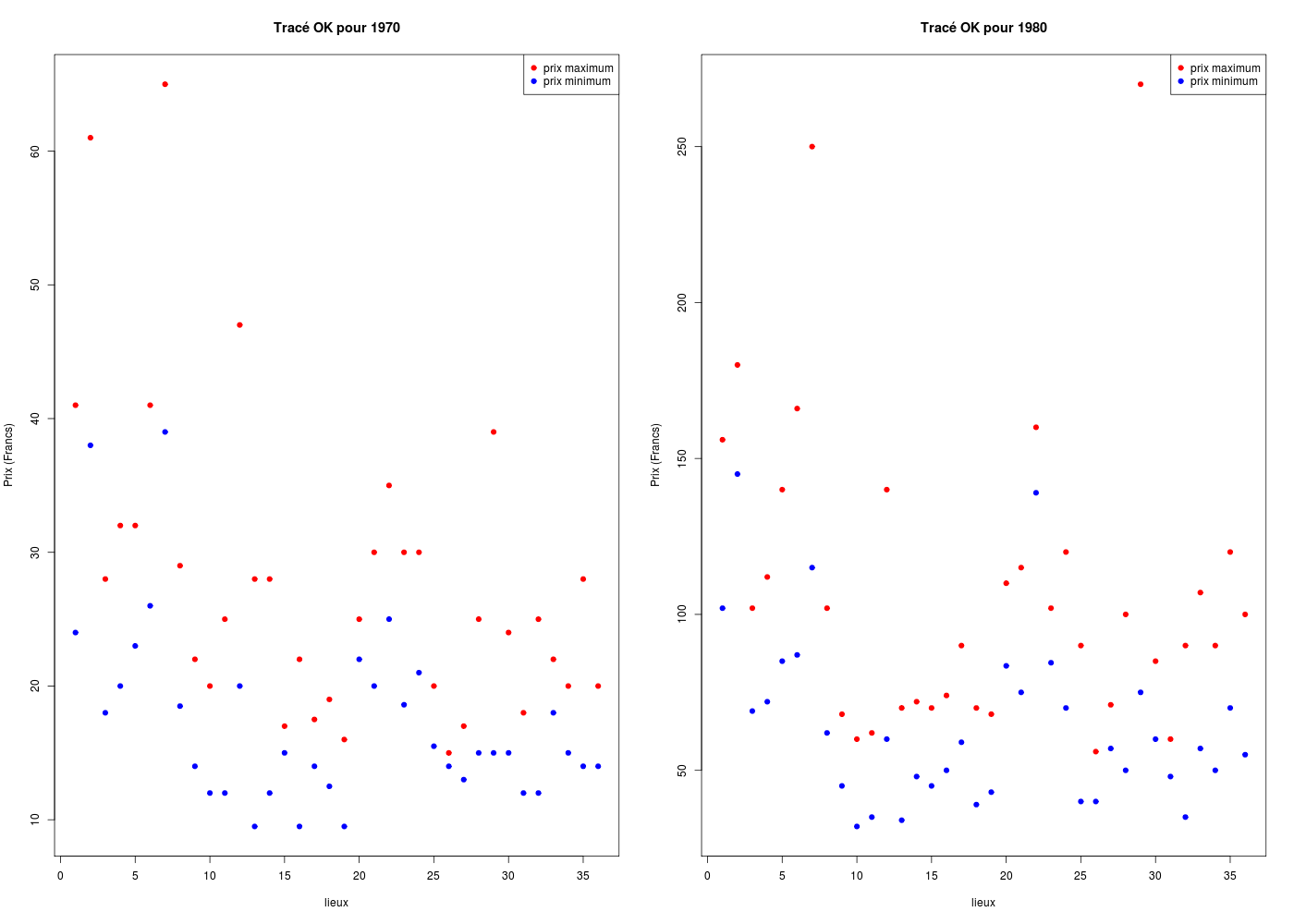
Pour effectuer plusieurs tracés dans des zones graphiques identiques, on peut utiliser les paramètres graphiques mfrow et mfcol
# lecture des fonctions (gH)
source("http://www.info.univ-angers.fr/~gh/statgh.r",encoding="latin1")
# lecture des données avec une fonction (gH)
loge <- lit.dar("http://www.info.univ-angers.fr/~gh/Datasets/logement.dar")
# deux tracés sur une même ligne
par(mfrow=c(1,2))
ymin <- min(c(loge$MI70,loge$MX70))
ymax <- max(c(loge$MI70,loge$MX70))
plot(loge$MI70,col="blue",pch=19,main="Tracé OK pour 1970",xlab="lieux",ylab="Prix (Francs)",ylim=c(ymin,ymax))
points(loge$MX70,col="red",pch=19)
legend(x="topright",legend=c("prix maximum","prix minimum"),col=c("red","blue"),pch=19)
ymin <- min(c(loge$MI80,loge$MX80))
ymax <- max(c(loge$MI80,loge$MX80))
plot(loge$MI80,col="blue",pch=19,main="Tracé OK pour 1980",xlab="lieux",ylab="Prix (Francs)",ylim=c(ymin,ymax))
points(loge$MX80,col="red",pch=19)
legend(x="topright",legend=c("prix maximum","prix minimum"),col=c("red","blue"),pch=19)
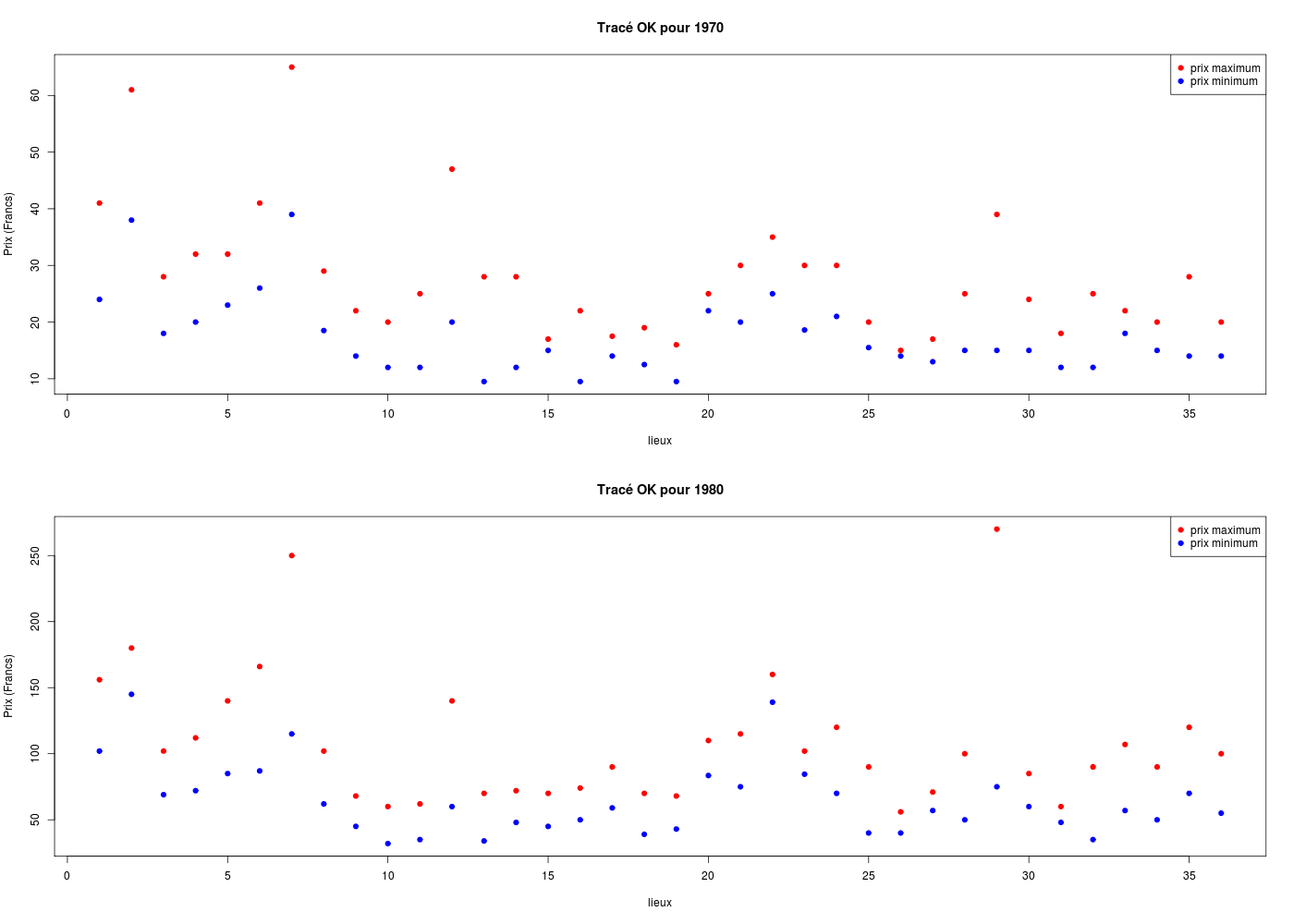
# deux tracés sur une même colonne
par(mfrow=c(2,1))
ymin <- min(c(loge$MI70,loge$MX70))
ymax <- max(c(loge$MI70,loge$MX70))
plot(loge$MI70,col="blue",pch=19,main="Tracé OK pour 1970",xlab="lieux",ylab="Prix (Francs)",ylim=c(ymin,ymax))
points(loge$MX70,col="red",pch=19)
legend(x="topright",legend=c("prix maximum","prix minimum"),col=c("red","blue"),pch=19)
ymin <- min(c(loge$MI80,loge$MX80))
ymax <- max(c(loge$MI80,loge$MX80))
plot(loge$MI80,col="blue",pch=19,main="Tracé OK pour 1980",xlab="lieux",ylab="Prix (Francs)",ylim=c(ymin,ymax))
points(loge$MX80,col="red",pch=19)
legend(x="topright",legend=c("prix maximum","prix minimum"),col=c("red","blue"),pch=19)
# retour à un graphique par tracé
par(mfrow=c(1,1))
# lecture des fonctions (gH)
source("http://www.info.univ-angers.fr/~gh/statgh.r",encoding="latin1")
# lecture des données avec une fonction (gH)
loge <- lit.dar("http://www.info.univ-angers.fr/~gh/Datasets/logement.dar")
# quatre tracés d'un coup
par(mfrow=c(2,2))
ymin <- min(c(loge$MI70,loge$MX70))
ymax <- max(c(loge$MI70,loge$MX70))
plot(loge$MI70,col="blue",pch=19,main="Tracé OK pour 1970",xlab="lieux",ylab="Prix (Francs)",ylim=c(ymin,ymax))
points(loge$MX70,col="red",pch=19)
legend(x="topright",legend=c("prix maximum","prix minimum"),col=c("red","blue"),pch=19)
ymin <- min(c(loge$MI80,loge$MX80))
ymax <- max(c(loge$MI80,loge$MX80))
plot(loge$MI80,col="blue",pch=19,main="Tracé OK pour 1980",xlab="lieux",ylab="Prix (Francs)",ylim=c(ymin,ymax))
points(loge$MX80,col="red",pch=19)
legend(x="topright",legend=c("prix maximum","prix minimum"),col=c("red","blue"),pch=19)
ymin <- min(c(loge$MI82,loge$MX82))
ymax <- max(c(loge$MI82,loge$MX82))
plot(loge$MI82,col="blue",pch=19,main="Tracé OK pour 1982",xlab="lieux",ylab="Prix (Francs)",ylim=c(ymin,ymax))
points(loge$MX82,col="red",pch=19)
legend(x="topright",legend=c("prix maximum","prix minimum"),col=c("red","blue"),pch=19)
ymin <- min(c(loge$MI86,loge$MX86))
ymax <- max(c(loge$MI86,loge$MX86))
plot(loge$MI86,col="blue",pch=19,main="Tracé OK pour 1986",xlab="lieux",ylab="Prix (Francs)",ylim=c(ymin,ymax))
points(loge$MX86,col="red",pch=19)
legend(x="topright",legend=c("prix maximum","prix minimum"),col=c("red","blue"),pch=19)
# retour à un graphique par tracé
par(mfrow=c(1,1))
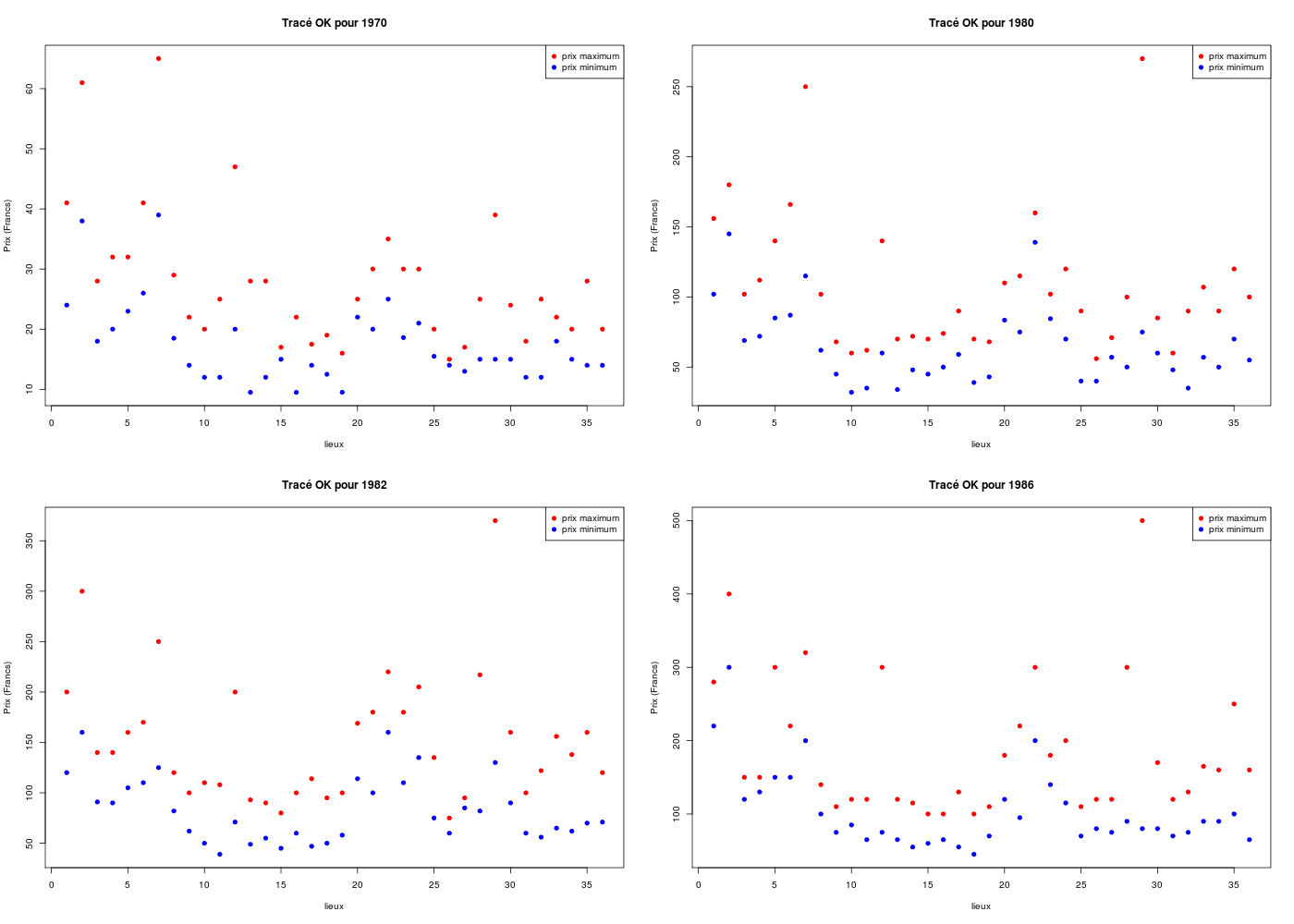
Il est clair qu'au vu d'une telle répétition de code, savoir programmer en R devient rapidement indispensable. Voici sans explications un exemple de fonction pour produire le même graphique à moindre frais :
# lecture des fonctions (gH)
source("http://www.info.univ-angers.fr/~gh/statgh.r",encoding="latin1")
# lecture des données avec une fonction (gH)
loge <- lit.dar("http://www.info.univ-angers.fr/~gh/Datasets/logement.dar")
# de l'intéret de savoir programmer des fonctions
plotmm <- function(an,df) { # sans commentaire ! (et ce n'est pas bien !!)
nomMin <- paste("MI",an,sep="")
nomMax <- paste("MX",an,sep="")
valMin <- df[,nomMin]
valMax <- df[,nomMax]
ymin <- min(c(valMin,valMax))
ymax <- max(c(valMin,valMax))
titre <- paste("Tracé pour l'année",an)
plot(valMin,col="blue",pch=19,main=titre,xlab="lieux",ylab="Prix (Francs)",ylim=c(ymin,ymax))
points(valMax,col="red",pch=19)
legend(x="topright",legend=c("prix maximum","prix minimum"),col=c("red","blue"),pch=19)
} # fin de fonction plotmm
par(mfrow=c(2,2))
plotmm("70",loge)
plotmm("80",loge)
plotmm("82",loge)
plotmm("86",loge)
par(mfrow=c(1,1)) # on remet 1 tracé par graphique
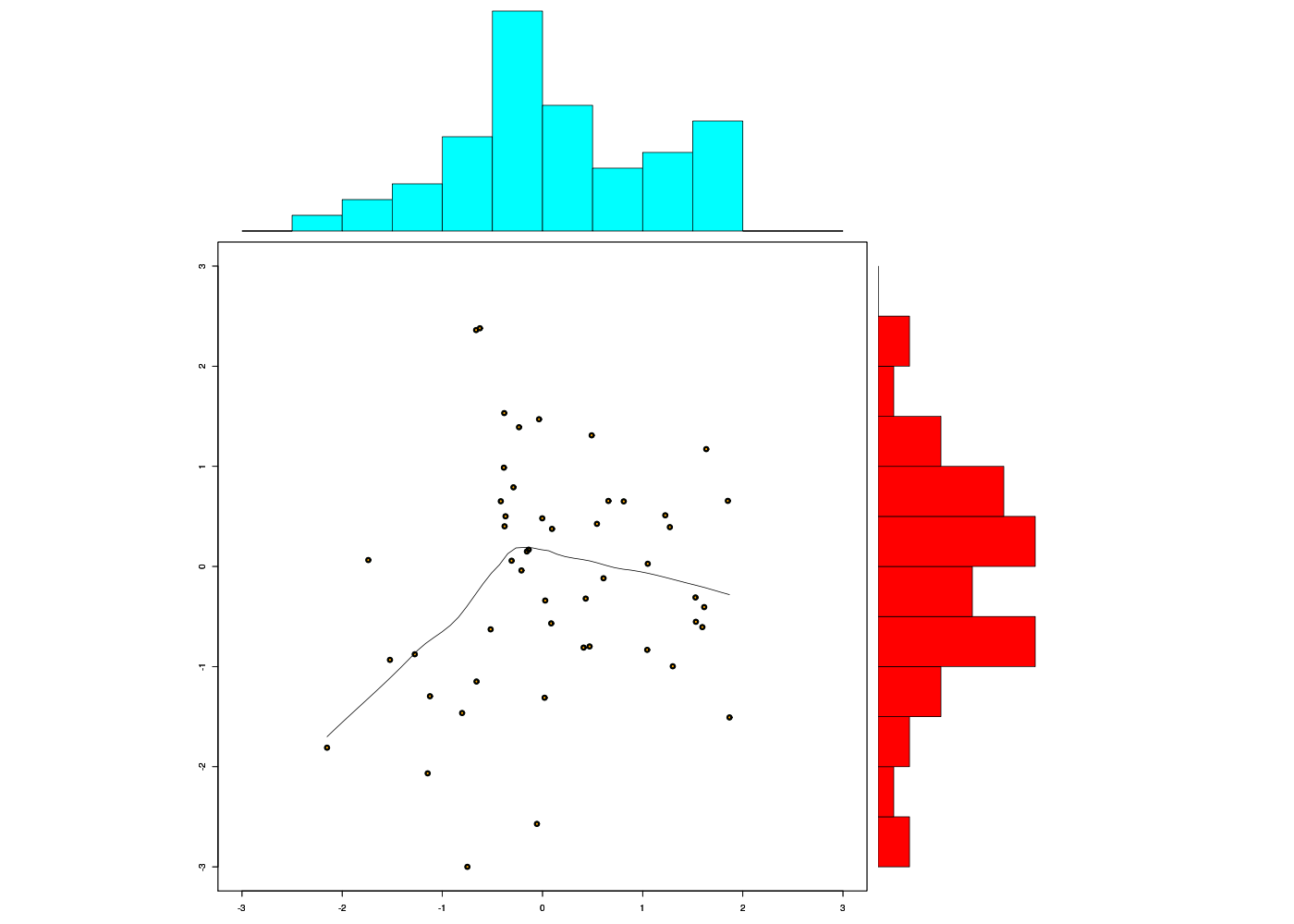
Signalons enfin que pour utiliser des zones de tracé inégales, il existe la fonction layout() dont voici un exemple d'utilisation, largement inspiré de example(layout) :
# plusieurs tracés dans des zones inégales avec layout
gr("layout.png")
##-- Create a scatterplot with marginal histograms -----
par(ask=FALSE) # pour éviter "Appuyez sur <Entrée> pour voir le graphique suivant :"
xx <- pmin(3, pmax(-3, stats::rnorm(50)))
yy <- pmin(3, pmax(-3, stats::rnorm(50)))
xhist <- hist(xx, breaks = seq(-3,3,0.5), plot = FALSE)
yhist <- hist(yy, breaks = seq(-3,3,0.5), plot = FALSE)
top <- max(c(xhist$counts, yhist$counts))
xrange <- c(-3, 3)
yrange <- c(-3, 3)
nf <- layout(matrix(c(2,0,1,3),2,2,byrow = TRUE), c(3,1), c(1,3), TRUE)
# tracé numéro 1
par(mar = c(3,3,1,1))
plot(xx, yy, xlim = xrange, ylim = yrange, xlab = "", ylab = "",col="darkgreen",pch=21,bg="orange",lwd=2)
par(new=TRUE)
scatter.smooth(xx,yy, xlim = xrange, ylim = yrange, xlab = "", ylab = "",lwd=3,lty=2)
# tracé numéro 2
par(mar = c(0,3,1,1))
barplot(xhist$counts, axes = FALSE, ylim = c(0, top), space = 0,col="cyan")
# tracé numéro 3
par(mar = c(3,0,1,1))
barplot(yhist$counts, axes = FALSE, xlim = c(0, top), space = 0, horiz = TRUE,col="red")
par(def.par) #- reset to default
par(ask=FALSE) # pour éviter "Appuyez sur <Entrée> pour voir le graphique suivant :"
par(mfrow=c(1,1))
dev.off()
5. Histogrammes de classes et de fréquences
Comment tracer des histogrammes de classes en R, par exemple pour les ages du dossier ELF ?
Comment tracer des histogrammes de fréquences en R, par exemple pour le code-sexe du dossier TITANIC ?
Si on devait tracer un histogramme de classes à la main pour des données quantitatives, il faudrait commencer par découper la variables en classes. Avec R, pas besoin de passer par la fonction cut() parce que la fonction hist() s'occupe de tout, mais il est possible, bien sûr de choisir le nombre de classes (via breaks). Dans la mesure où la fonction density() réalise l'estimation par noyau (au sens de de Parzen-Rozenblatt) de la densité de probabilité de la variable aléatoire sous-jacente, il est facile de tracer cette densité à laquelle nous conseillons d'adjoindre la loi normale associée à la moyenne et à l'écart-type des données, ce qui se réalise très simplement avec dnorm() et curve(). Enfin, si on complète le graphique avec des indications de densité sur l'axe des X grâce à rug(), on dispose d'un graphique assez complet pour apprécier la distribution des données.
# un histogramme de classes se trace avec hist() pour des données numériques
# lecture des données (gH)sur Internet
elf <- lit.dar("http://www.info.univ-angers.fr/~gh/Datasets/elf.dar")
ages <- elf$AGE
# pour avoir deux histogrammes sur une même ligne
par(mfrow=c(1,2))
# un tracé minimaliste
hist(ages)
# un tracé un peu plus statistique, avec la loi normale candidate sous-jacente,
# la courbe de la densité estimée, un "peigne" de la répartition sur l'axe x...
hist(ages,col="yellow",main="Distribution des ages",probability=TRUE,xlab="données ELF")
rug(ages,col="darkgreen")
lines(density(ages),col="red",lwd=2)
vnorm <- function(x) { dnorm(x,mean=mean(ages),sd=sd(ages)) }
curve(vnorm,add=TRUE,col="blue",lwd=2)
legend(x="topright",legend=c("densité estimée","loi normale associée"),col=c("red","blue"),cex=0.6,lwd=2)
# retour à un graphique par tracé
par(mfrow=c(1,1))
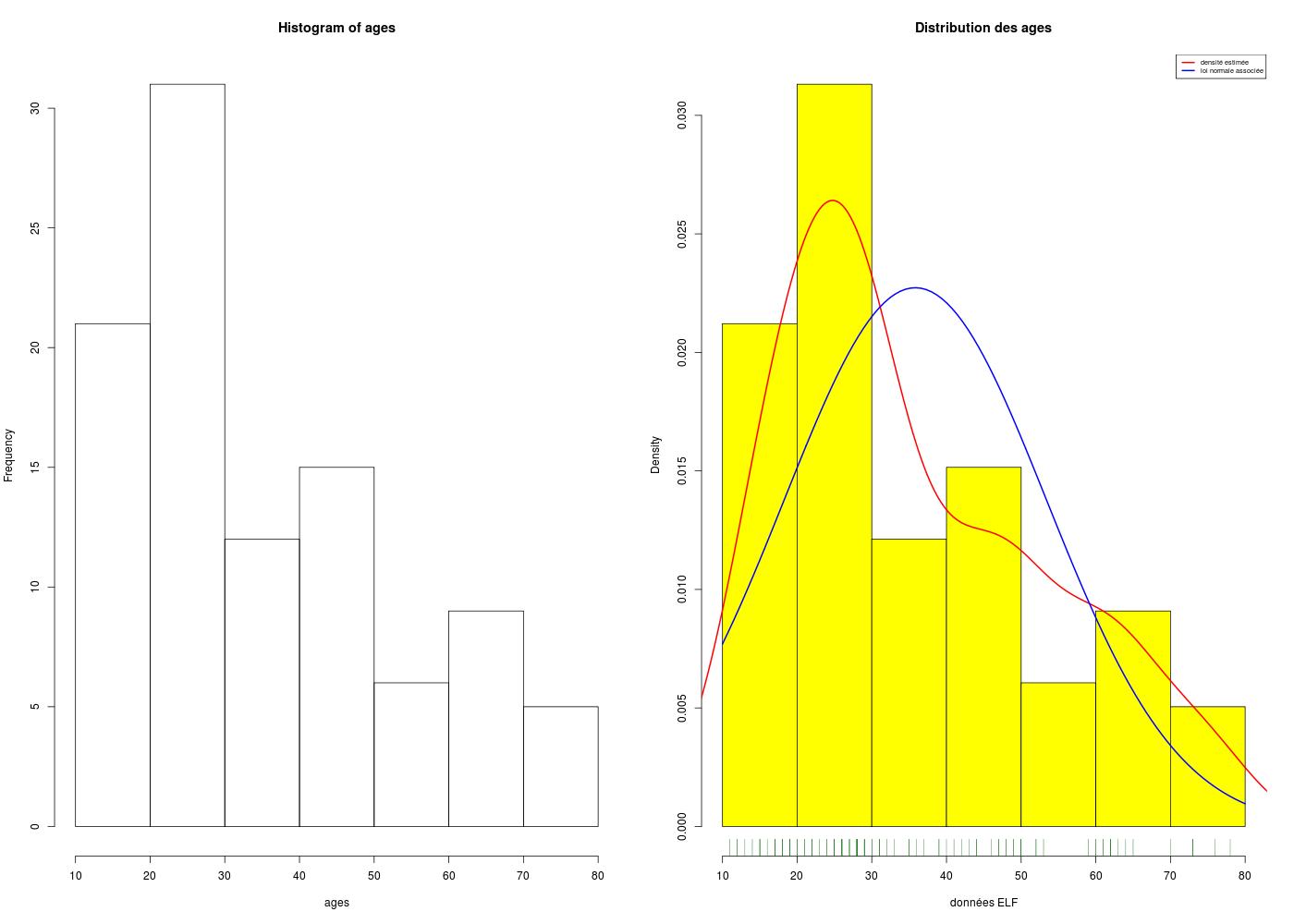
Remarque : si on spécifie plot=FALSE dans l'appel à hist(), on peut voir quel découpage a été réalisé. En particulier, cela peut permettre de fournir les "bonnes" valeurs à cut().
elf <- lit.dar("http://www.info.univ-angers.fr/~gh/Datasets/elf.dar")
ages <- elf$AGE
hist(ages,plot=FALSE)
cut(ages,breaks=8)
cut(ages,breaks=10*(1:8))
> elf <- lit.dar("http://www.info.univ-angers.fr/~gh/Datasets/elf.dar")
> ages <- elf$AGE
> hist(ages,plot=FALSE)
$breaks
[1] 10 20 30 40 50 60 70 80
$counts
[1] 21 31 12 15 6 9 5
$density
[1] 0.021212121 0.031313131 0.012121212 0.015151515 0.006060606 0.009090909
[7] 0.005050505
$mids
[1] 15 25 35 45 55 65 75
$xname
[1] "ages"
$equidist
[1] TRUE
attr(,"class")
[1] "histogram"
> cut(ages,breaks=8)
[1] (61.3,69.7] (52.9,61.3] (27.7,36.1] (19.3,27.7] (19.3,27.7] (69.7,78.1]
[7] (10.9,19.3] (52.9,61.3] (61.3,69.7] (61.3,69.7] (61.3,69.7] (10.9,19.3]
[13] (69.7,78.1] (19.3,27.7] (44.5,52.9] (44.5,52.9] (44.5,52.9] (36.1,44.5]
[19] (19.3,27.7] (19.3,27.7] (27.7,36.1] (44.5,52.9] (61.3,69.7] (19.3,27.7]
[25] (10.9,19.3] (36.1,44.5] (52.9,61.3] (10.9,19.3] (27.7,36.1] (19.3,27.7]
[31] (36.1,44.5] (36.1,44.5] (69.7,78.1] (10.9,19.3] (36.1,44.5] (36.1,44.5]
[37] (10.9,19.3] (10.9,19.3] (44.5,52.9] (52.9,61.3] (10.9,19.3] (19.3,27.7]
[43] (69.7,78.1] (36.1,44.5] (52.9,61.3] (19.3,27.7] (44.5,52.9] (69.7,78.1]
[49] (10.9,19.3] (36.1,44.5] (27.7,36.1] (19.3,27.7] (27.7,36.1] (19.3,27.7]
[55] (44.5,52.9] (27.7,36.1] (44.5,52.9] (27.7,36.1] (27.7,36.1] (27.7,36.1]
[61] (27.7,36.1] (27.7,36.1] (27.7,36.1] (19.3,27.7] (27.7,36.1] (27.7,36.1]
[67] (19.3,27.7] (19.3,27.7] (19.3,27.7] (27.7,36.1] (27.7,36.1] (27.7,36.1]
[73] (27.7,36.1] (10.9,19.3] (19.3,27.7] (10.9,19.3] (10.9,19.3] (10.9,19.3]
[79] (10.9,19.3] (19.3,27.7] (19.3,27.7] (10.9,19.3] (19.3,27.7] (19.3,27.7]
[85] (69.7,78.1] (52.9,61.3] (44.5,52.9] (44.5,52.9] (19.3,27.7] (10.9,19.3]
[91] (44.5,52.9] (27.7,36.1] (10.9,19.3] (10.9,19.3] (27.7,36.1] (10.9,19.3]
[97] (36.1,44.5] (61.3,69.7] (44.5,52.9]
8 Levels: (10.9,19.3] (19.3,27.7] (27.7,36.1] (36.1,44.5] ... (69.7,78.1]
> cut(ages,breaks=10*(1:8))
[1] (60,70] (50,60] (30,40] (20,30] (20,30] (60,70] (10,20] (50,60] (60,70]
[10] (60,70] (60,70] (10,20] (70,80] (10,20] (40,50] (40,50] (40,50] (40,50]
[19] (20,30] (20,30] (20,30] (40,50] (60,70] (20,30] (10,20] (40,50] (60,70]
[28] (10,20] (20,30] (20,30] (40,50] (30,40] (70,80] (10,20] (30,40] (40,50]
[37] (10,20] (10,20] (40,50] (60,70] (10,20] (10,20] (70,80] (30,40] (50,60]
[46] (20,30] (50,60] (70,80] (10,20] (40,50] (20,30] (20,30] (20,30] (20,30]
[55] (40,50] (20,30] (50,60] (30,40] (20,30] (20,30] (20,30] (20,30] (20,30]
[64] (20,30] (20,30] (30,40] (20,30] (20,30] (20,30] (20,30] (30,40] (30,40]
[73] (30,40] (10,20] (20,30] (10,20] (10,20] (10,20] (10,20] (20,30] (20,30]
[82] (10,20] (20,30] (20,30] (70,80] (50,60] (40,50] (40,50] (20,30] (10,20]
[91] (40,50] (30,40] (10,20] (10,20] (30,40] (10,20] (30,40] (60,70] (40,50]
Levels: (10,20] (20,30] (30,40] (40,50] (50,60] (60,70] (70,80]
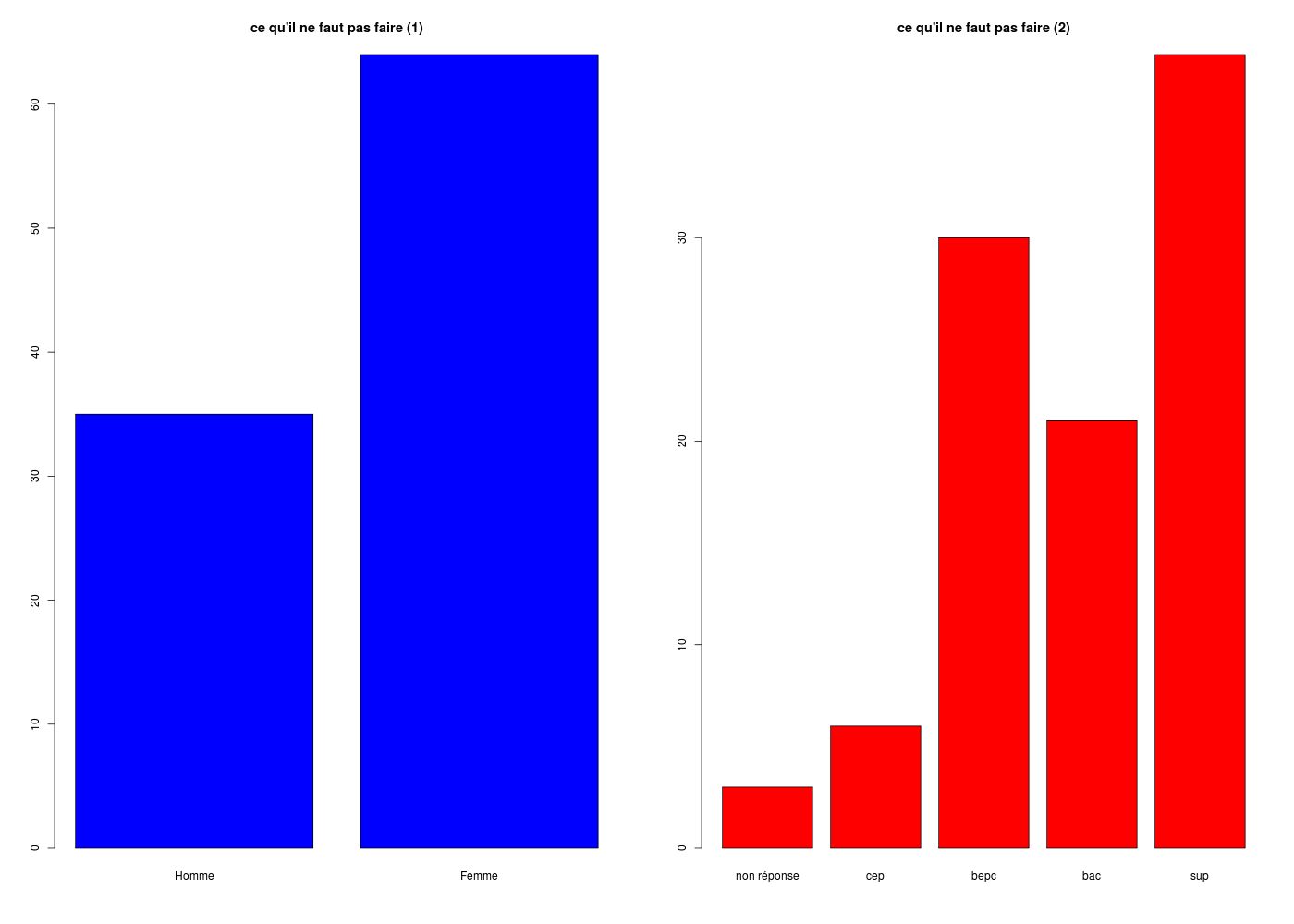
Réaliser l'histogramme des fréquences des modalités d'une variable qualitative se fait non pas avec hist() qui génére des barres contigües mais avec barplot() dont les barres sont nettement séparées. Comme avec Excel, le tracé par défaut utilise des effectifs absolus (donc des comptages au lieu de pourcentages) avec un axe Y borné par la plus grande fréquence. Cette représentation est souvent trompeuse lorsqu'on veut comparer des fréquences. Il vaut mieux utiliser des fréquences relatives et tracer sur l'intervalle [0,1] pour Y. La commande example(barplot) montre comment réaliser des histogrammes de fréquences cumulées et conjointes.
elf <- lit.dar("http://www.info.univ-angers.fr/~gh/Datasets/elf.dar")
sexe <- factor(elf$SEXE,levels=0:1,labels=c("Homme","Femme"))
etud <- factor(elf$ETUD,levels=0:4,labels=c("non réponse","cep","bepc","bac","sup"))
# premier tracé, incorrect (axes différents)
gr("barplot01.png")
par(mfrow=c(1,2))
barplot(table(sexe),main="ce qu'il ne faut pas faire (1)",col="blue")
barplot(table(etud),main="ce qu'il ne faut pas faire (2)",col="red")
dev.off()
# second tracé, correct (axes égaux et de plus de 0 à 100 %)
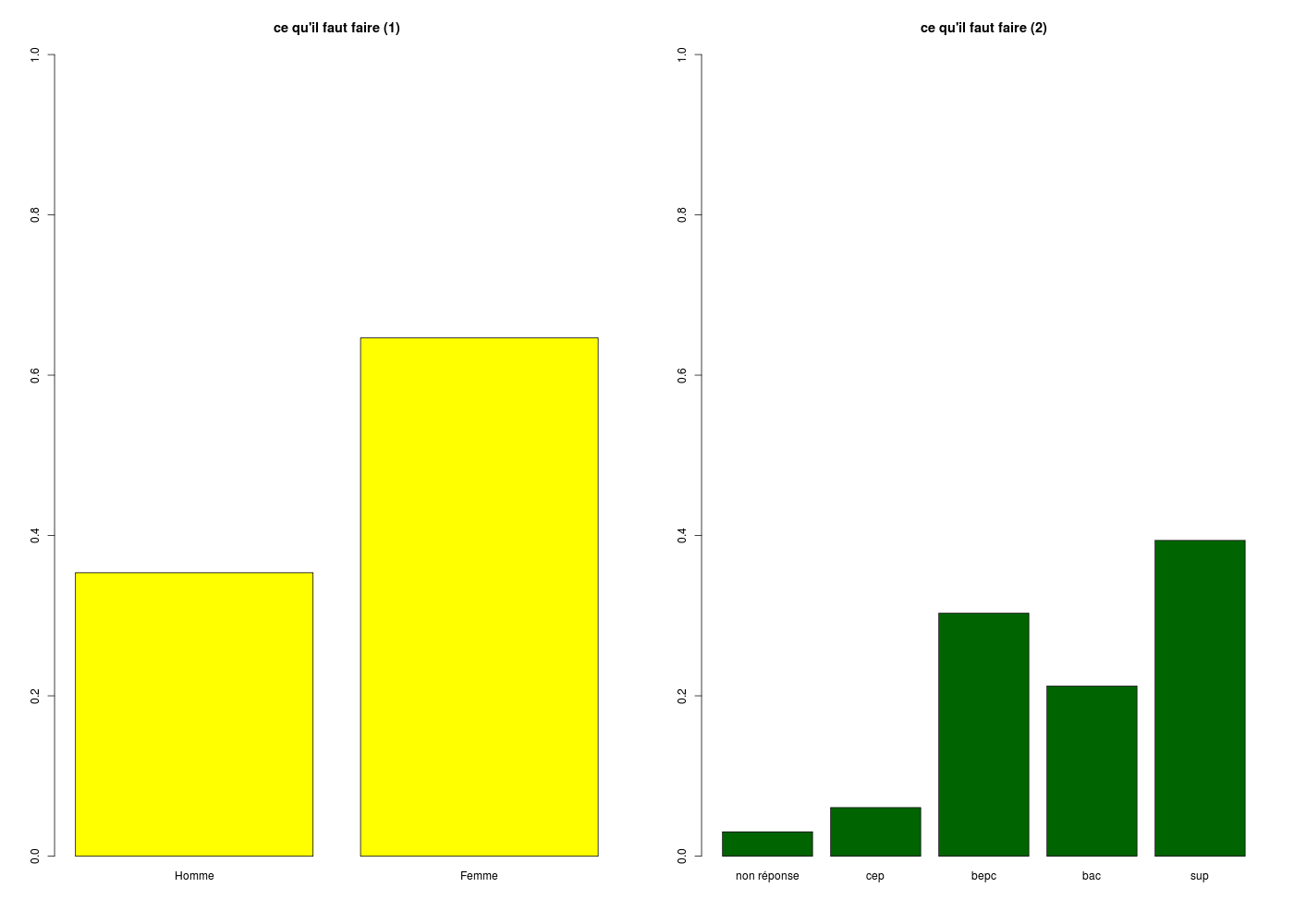
gr("barplot02.png")
par(mfrow=c(1,2))
barplot(table(sexe)/length(sexe),ylim=c(0,1),main="ce qu'il faut faire (1)",col="yellow")
barplot(table(etud)/length(etud),ylim=c(0,1),main="ce qu'il faut faire (2)",col="darkgreen")
dev.off()
par(mfrow=c(1,1))
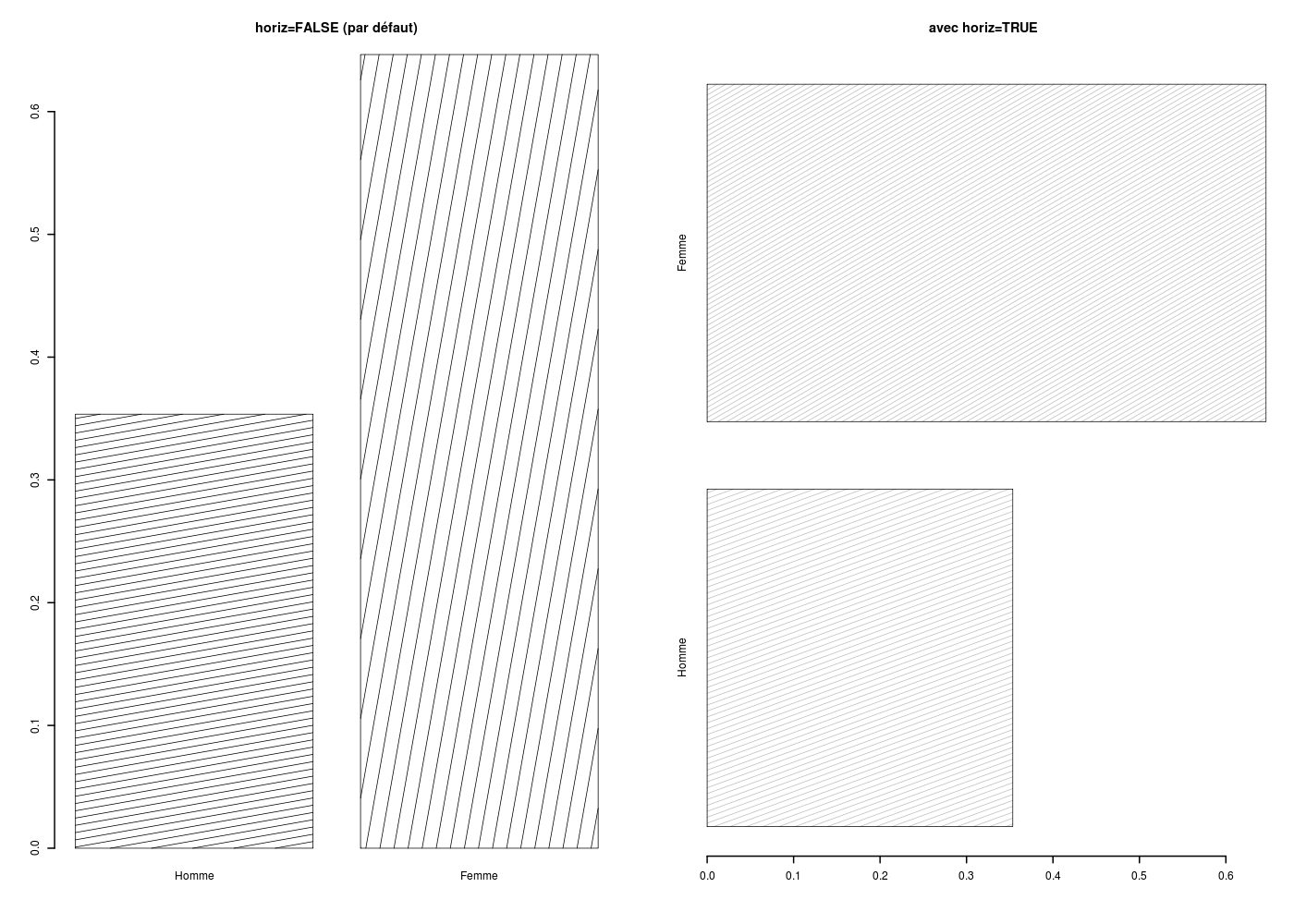
Pour réaliser des histogrammes de fréquences horizontaux plutôt que verticaux, il faut écrire horiz=TRUE et si on doit réaliser des graphiques en noir et blanc pour publication, on utilise les paramètres graphiques density et angle :
elf <- lit.dar("http://www.info.univ-angers.fr/~gh/Datasets/elf.dar")
sexe <- factor(elf$SEXE,levels=0:1,labels=c("Homme","Femme"))
etud <- factor(elf$ETUD,levels=0:4,labels=c("non réponse","cep","bepc","bac","sup"))
gr("barplot03.png")
par(mfrow=c(1,2))
barplot(
table(sexe)/length(sexe),
density=c(9.3,4.8),
angle=c(10,80),
lwd=2,
col="black",
main="horiz=FALSE (par défaut)"
) # fin de barplot
barplot(
table(sexe)/length(sexe),
density=c(12,15),
angle=c(20,30),
lwd=2,
col="grey",
horiz=TRUE,
main="avec horiz=TRUE"
) # fin de barplot
dev.off()
Lorsqu'on trace des histogrammes de fréquences pour des données ne se référant pas au même échantillon, il est en général incorrect d'utiliser des effectifs absolus.
# un histogramme de fréquences se trace avec barplot() pour des données "facteur"
# car sinon les barres ont des labels correspondant au code de la modalité
# rappel : il est conseillé de tracer des pourcentages sur un axe de 0 à 100 % en y
# lecture des données gH (numériques) sur Internet
titanic <- lit.dar("http://www.info.univ-angers.fr/~gh/Datasets/titanic.dar")
# conversion numérique vers variable qualitative
sexesF <- factor(titanic$SEX,levels=0:1,labels=c("Femme","Homme"))
# pour avoir deux histogrammes sur une même ligne
par(mfrow=c(1,2))
# un tracé minimaliste et incorrect
barplot(table(titanic$SEX))
# un tracé un peu plus sophistiqué
barplot(
table(sexesF)/length(sexesF),
col="red",
main="Répartition des codes-sexe",
ylim=c(0,1),
sub="(données Titanic)"
) # fin de barplot
# retour à un graphique par tracé
par(mfrow=c(1,1))
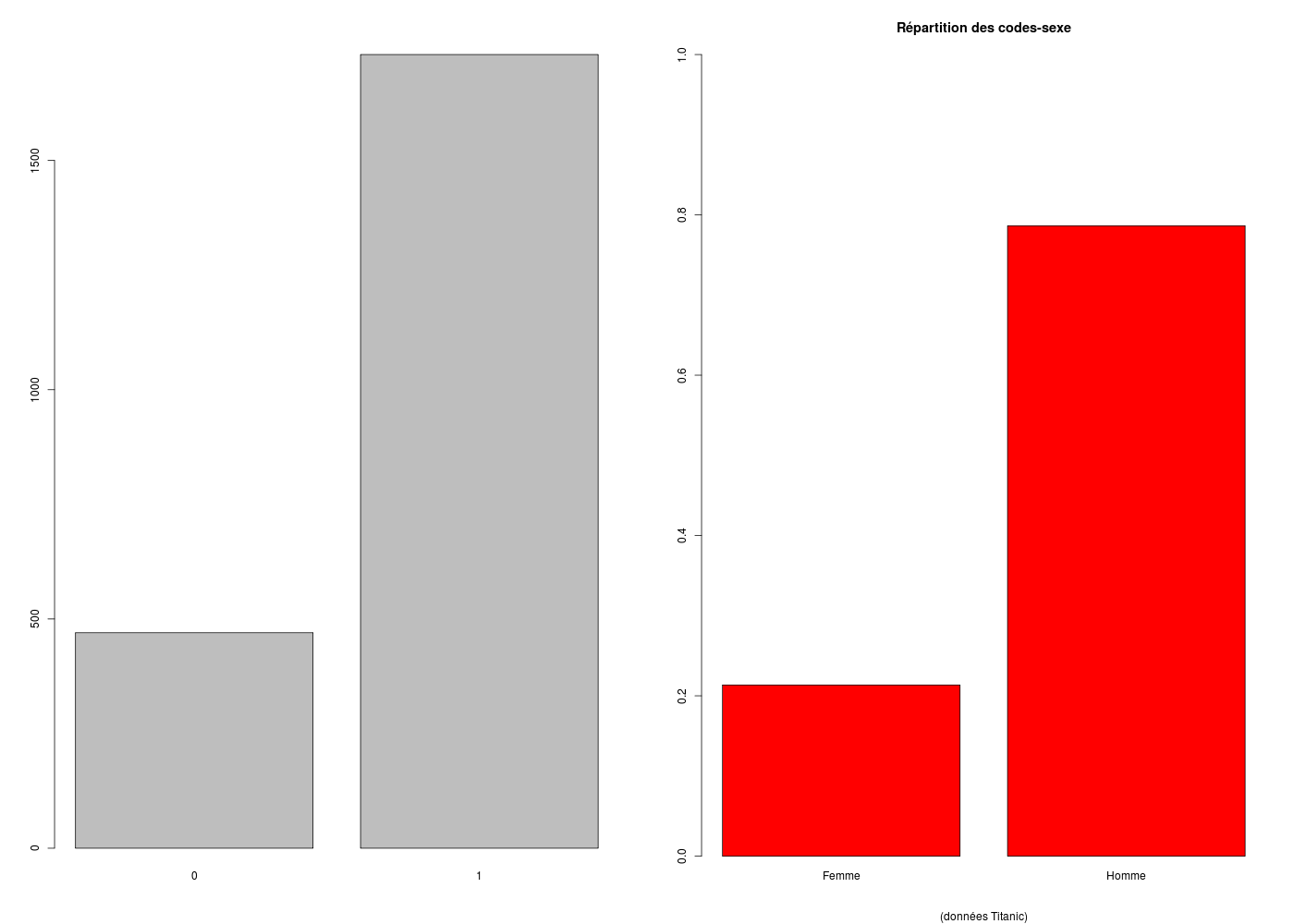
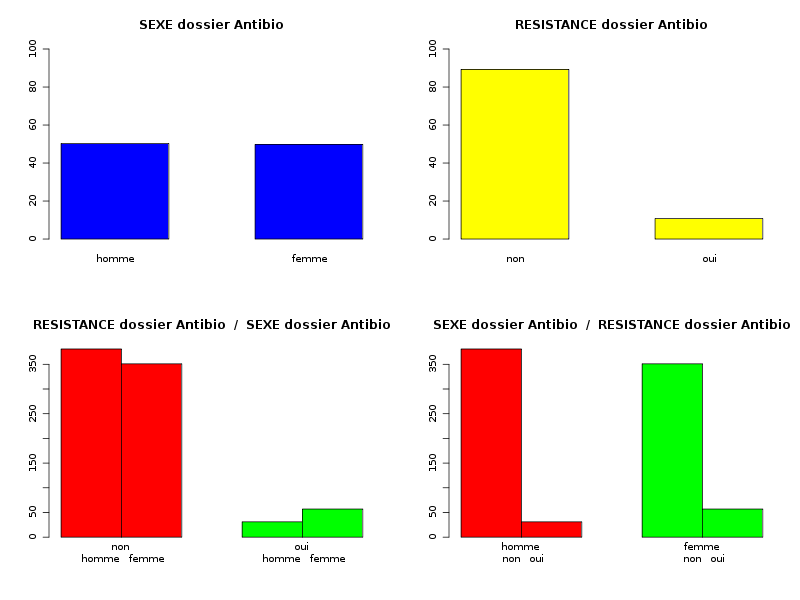
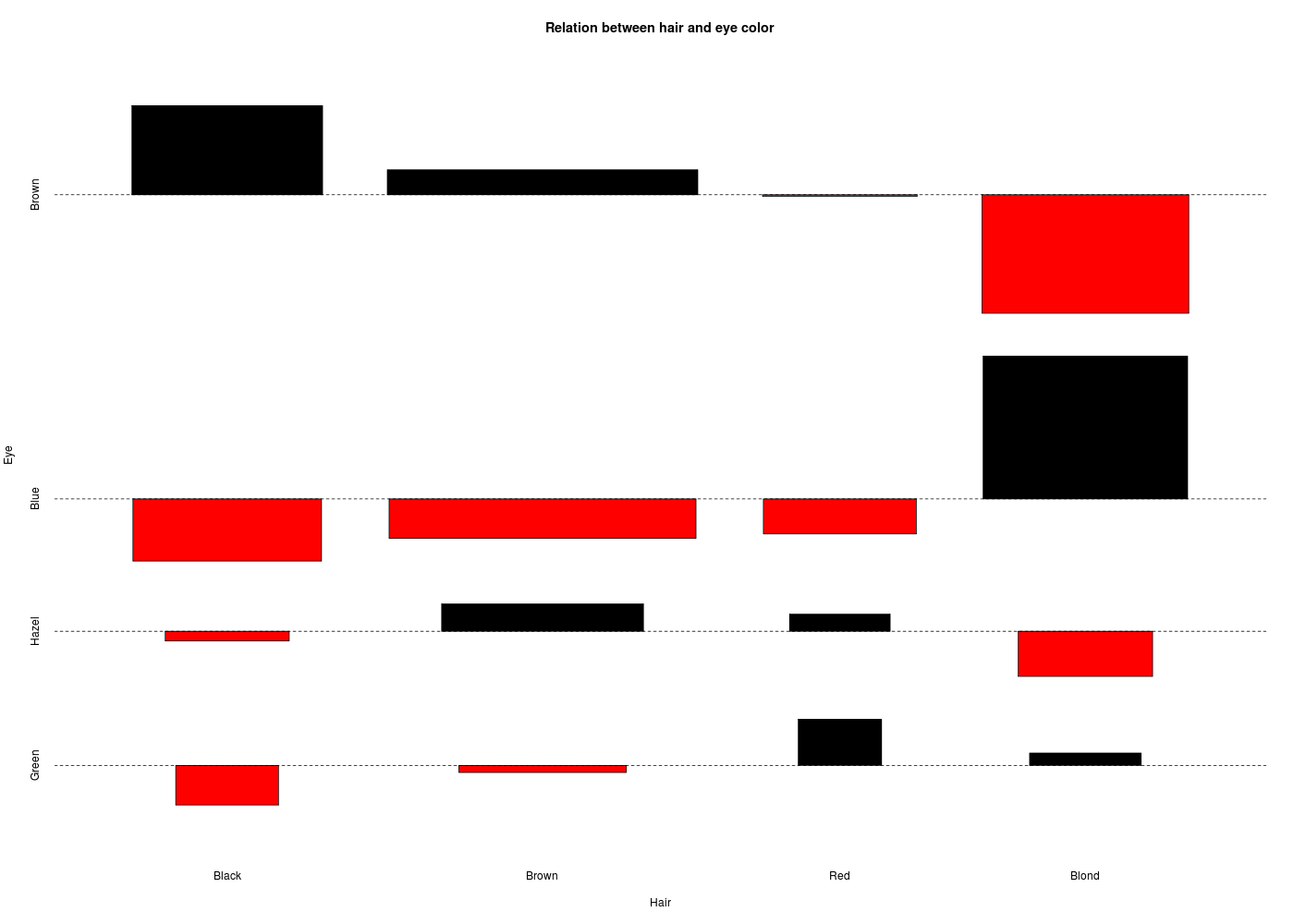
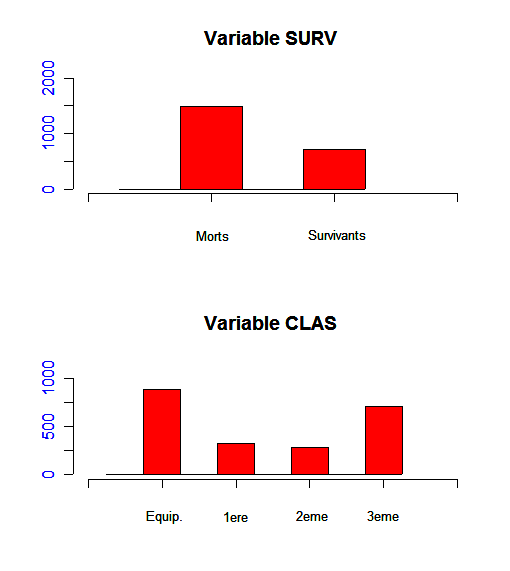
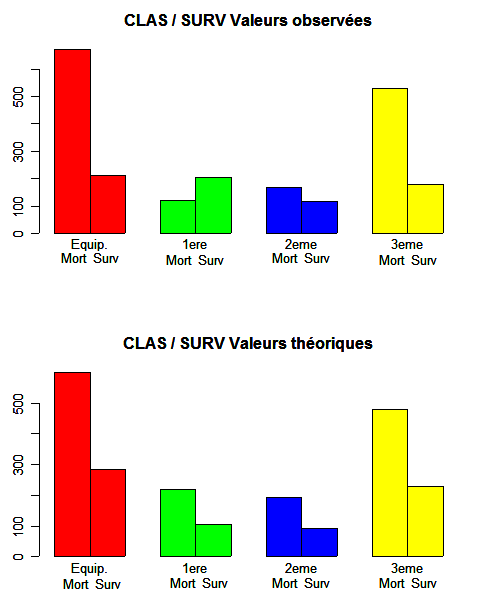
En cas d'histogrammes de fréquences pour des tris croisés, il faut bien réfléchir au sens de croisement. Etes-vous capable de voir lequel des deux croisements ci-dessous est «intéressant» ?
6. "Boxplots" et consor
Qu'est-ce qu'un boxplot ? Comment tracer des boxplots en R ? Avec ou sans encoche ?
Qu'est-ce qu'un beanplot ? Et un violinplot ? Et un stemleaf ?
Un tracé en boxplot ou
graphique de Tukey
est souvent nommé en France
«boite à moustaches». Basé presque toujours (sauf pour Statistica) sur les
quartiles, il permet de représenter la tendance centrale et la
dispersion des données. Il existe des variantes. Nous fournissons ci-dessous quelques liens pour approfondir.
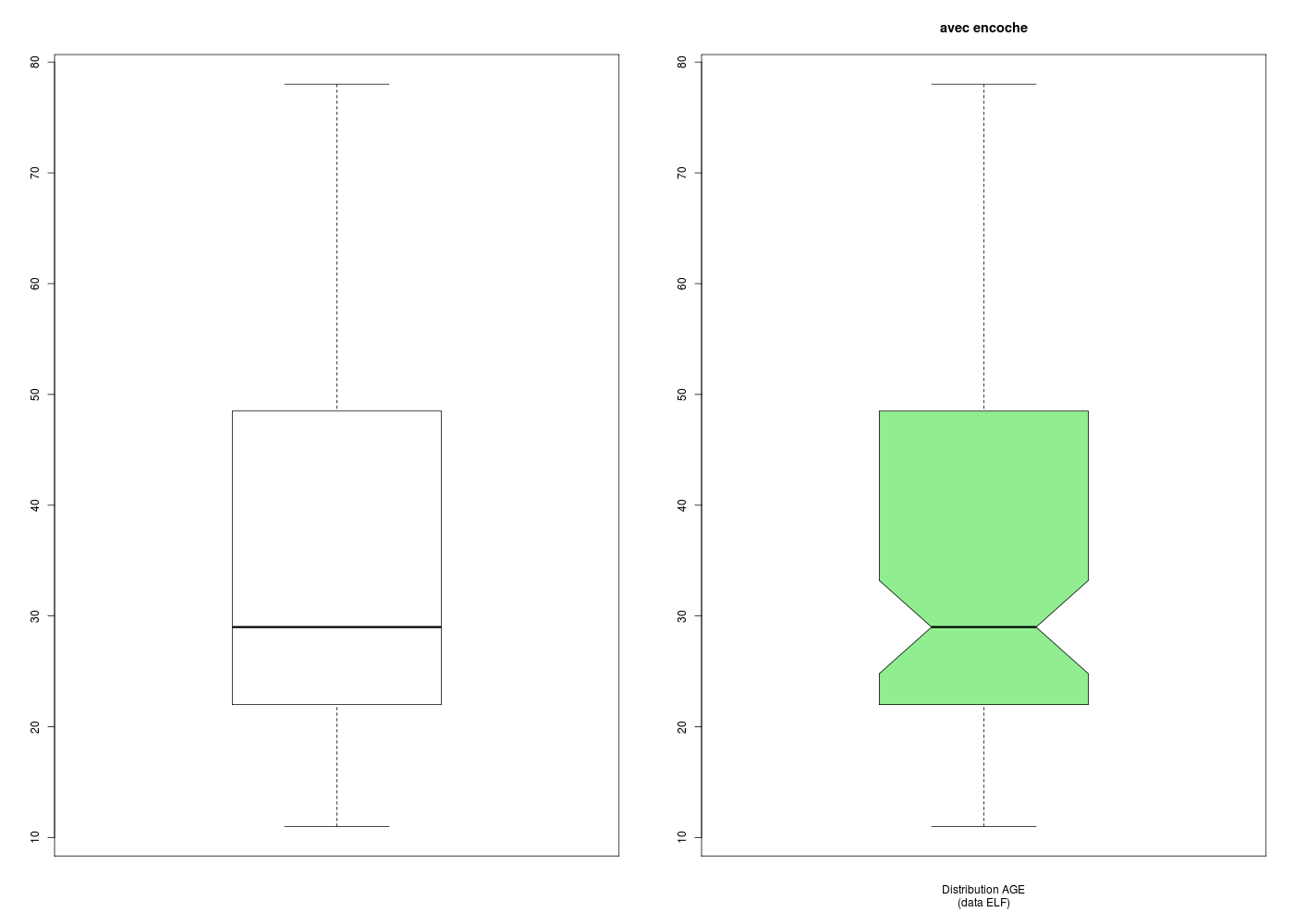
Pour R, la fonction associée se nomme tout naturellement boxplot() et comporte de nombreuses options.
elf <- lit.dar("http://www.info.univ-angers.fr/~gh/Datasets/elf.dar")
ages <- elf$AGE
par(mfrow=c(1,2))
boxplot(ages)
# ==> il faut noter l'astuce du dernier \n pour "remonter sub"
boxplot(
ages,
notch=TRUE,
main="avec encoche",
col="lightgreen",
sub="Distribution AGE\n(data ELF)\n"
) # fin de boxplot
par(mfrow=c(1,1))
# pour avoir les informations de tracé :
boxplot(ages,plot=FALSE)
> elf <- lit.dar("http://www.info.univ-angers.fr/~gh/Datasets/elf.dar")
> ages <- elf$AGE
> par(mfrow=c(1,2))
> boxplot(ages)
> # ==> il faut noter l'astuce du dernier \n pour remonter sub
>
> boxplot(
+ ages,
+ notch=TRUE,
+ main="avec encoche",
+ col="lightgreen",
.... [TRUNCATED]
> par(mfrow=c(1,1))
> boxplot(ages,plot=FALSE)
$stats
[,1]
[1,] 11.0
[2,] 22.0
[3,] 29.0
[4,] 48.5
[5,] 78.0
attr(,"class")
1
"integer"
$n
[1] 99
$conf
[,1]
[1,] 24.79191
[2,] 33.20809
$out
numeric(0)
$group
numeric(0)
$names
[1] "1"
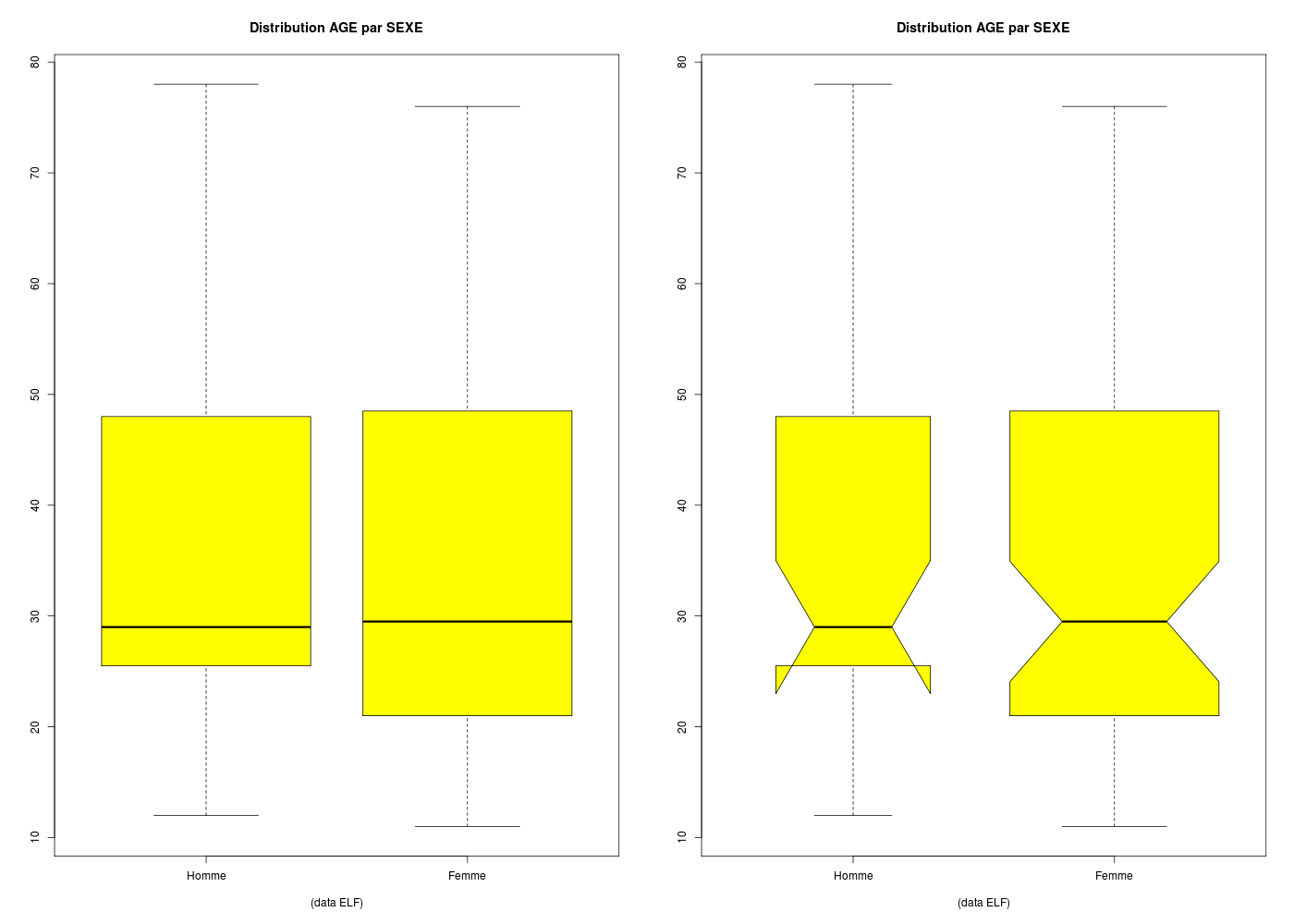
Les boxplots sont très pratiques pour comparer des groupes, mais le paramètre varwidth n'est pas toujours très efficace.
elf <- lit.dar("http://www.info.univ-angers.fr/~gh/Datasets/elf.dar")
ages <- elf$AGE
sexs <- factor(elf$SEXE,levels=0:1,labels=c("Homme","Femme"))
par(mfrow=c(1,2))
boxplot(
ages~sexs,
col="yellow",
main="Distribution AGE par SEXE",
sub="(data ELF)\n",
) # fin de boxplot
#avec encoche et largeur proportionnelle à l'effectif
boxplot(
ages~sexs,
col="yellow",
main="Distribution AGE par SEXE",
sub="(data ELF)\n",
notch=TRUE,
varwidth=TRUE
) # fin de boxplot
par(mfrow=c(1,1))
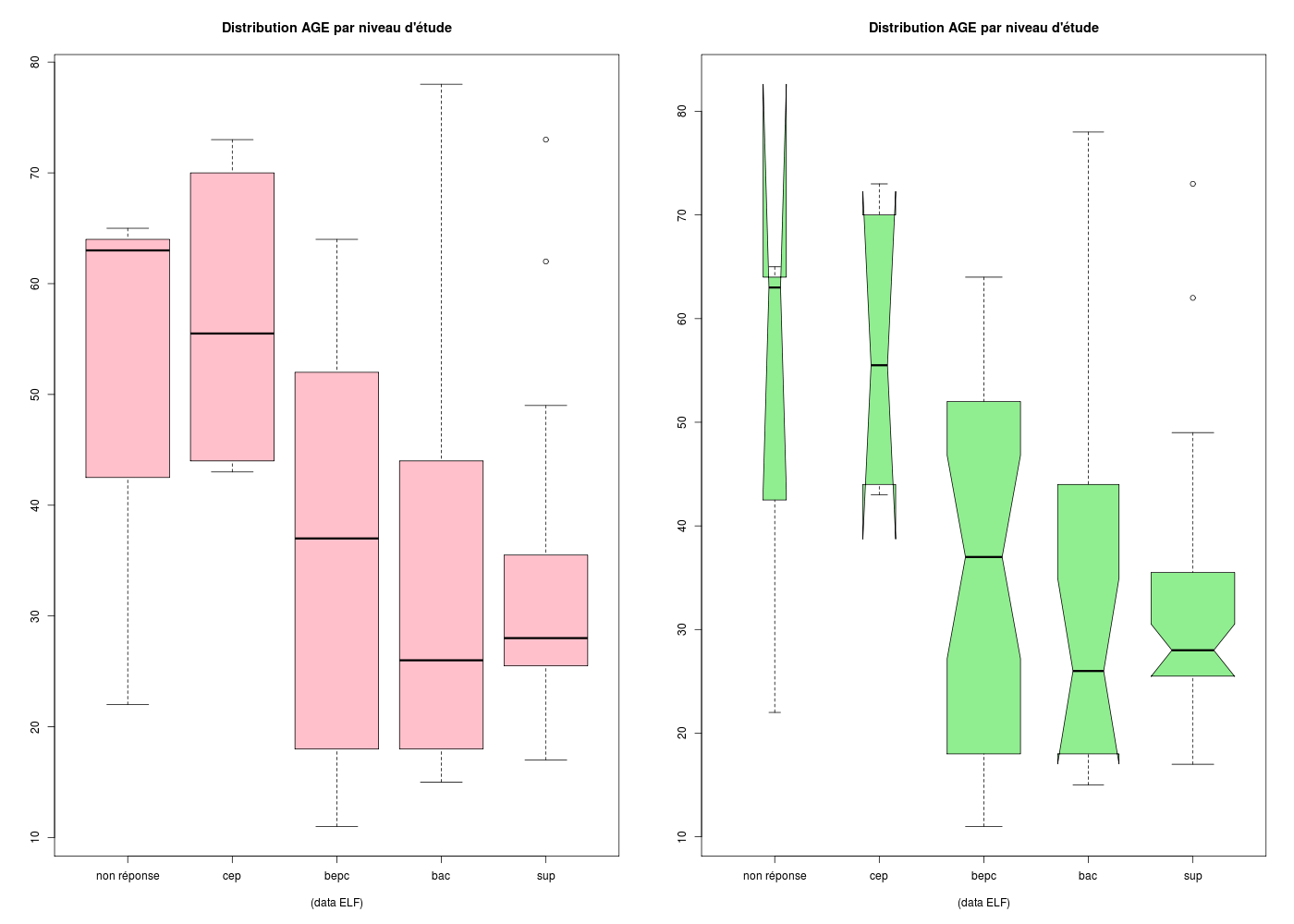
Les encoches (notch en anglais) permettent de visualiser les intervalles de confiance de la mediane mais présentent parfois des inversions.
elf <- lit.dar("http://www.info.univ-angers.fr/~gh/Datasets/elf.dar")
ages <- elf$AGE
etud <- factor(elf$ETUD,levels=0:4,labels=c("non réponse","cep","bepc","bac","sup"))
par(mfrow=c(1,2))
boxplot(
ages~etud,
col="pink",
main="Distribution AGE par niveau d'étude",
sub="(data ELF)\n",
) # fin de boxplot
#avec encoche et largeur proportionnelle à l'effectif
boxplot(
ages~etud,
col="lightgreen",
main="Distribution AGE par niveau d'étude",
sub="(data ELF)\n",
notch=TRUE,
varwidth=TRUE
) # fin de boxplot
par(mfrow=c(1,1))
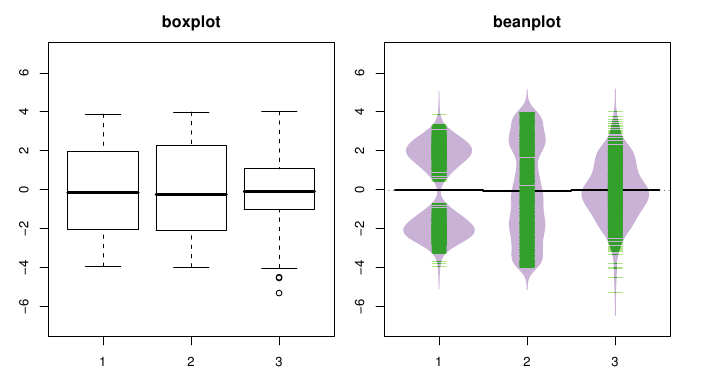
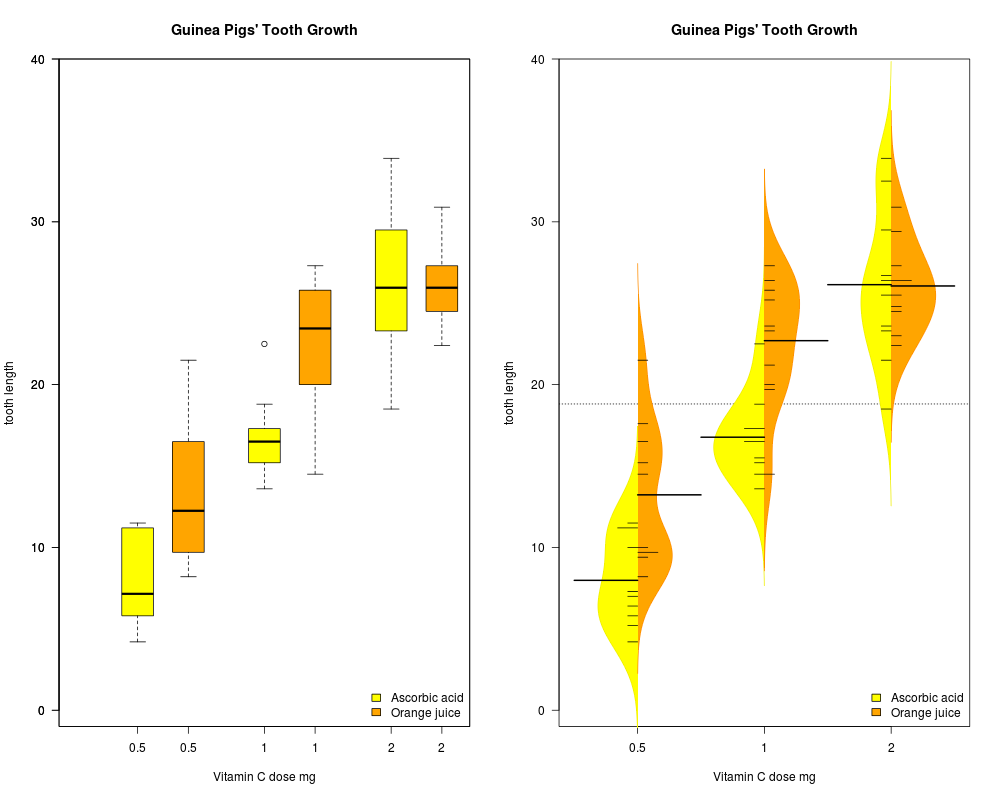
Les boxplots ne sont pas adaptés aux distributions bimodales ni multimodales. Les beanplots le sont. Voir le PDF du package beanplot La principale fonction associée est bien sûr beanplot(). Voici un exemple parlant :
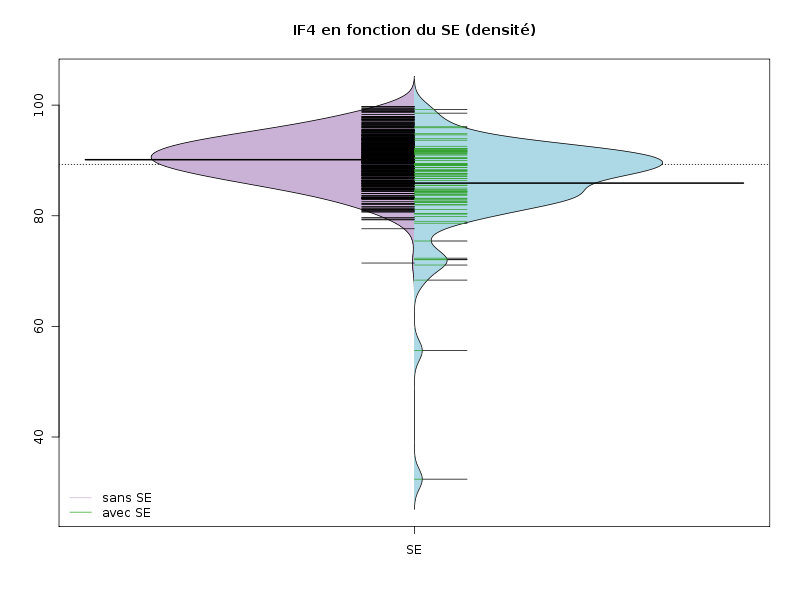
Les demi-beanplots sont très pratiques pour comparer des variables qualitatives binaires
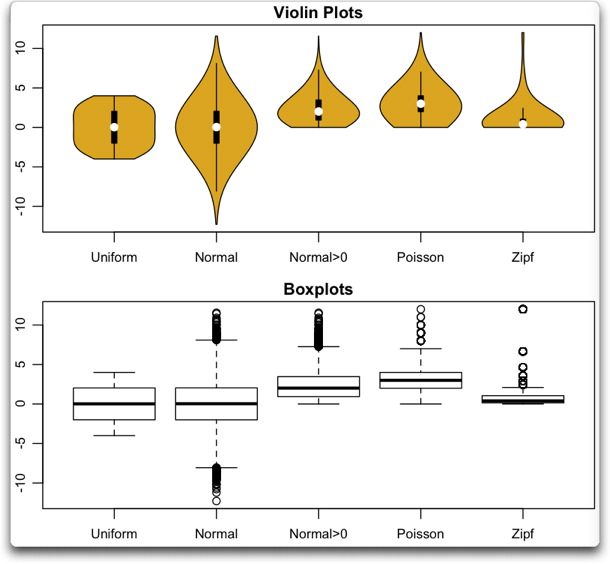
Les violinplots sont assez similaires aux beanplots. Une implémentation en R est dans le package vioplot, fonction vioplot().
Une autre implémentation est fournie par la fonction geom_violin() du package ggplot2 avec des possibilités intéressantes.
Contrairement aux précédents tracés, un diagramme stemleaf ou en tige et feuilles en français
est une façon de trier et d'afficher les données de façon à faire ressortir des tendances,
un peu comme un histogramme de classes, mais en mode texte.
lea <- lit.dar("http://www.info.univ-angers.fr/~gh/Datasets/lea.dar")
# tracé tige etfeuille standard
stem(lea$length)
# utilisation de scale
stem(lea$length,scale=2)
# utilisation de width
stem(lea$length,width=130)
# autres exemples
elf <- lit.dar("http://www.info.univ-angers.fr/~gh/Datasets/elf.dar")
stem(elf$AGE)
her <- lit.dar("http://www.info.univ-angers.fr/~gh/Datasets/her.dar")
stem(her$age)
> lea <- lit.dar("http://www.info.univ-angers.fr/~gh/Datasets/lea.dar")
> # tracé tige etfeuille standard
>
> stem(lea$length)
The decimal point is 2 digit(s) to the right of the |
0 | 77777888888899999999999999999999999999999999999999999999999999999999
1 | 00000000000000000000000000000000000000000000000111111111111111111111+323
2 | 00000000000000000000000000001111111111111111222222222222223333333333+107
3 | 000000011111222223333344444445556666788889999
4 | 0011111112223444556666777778889
5 | 0122455667888
6 | 22344588
7 | 234
8 | 5
9 |
10 |
11 |
12 | 4
13 |
14 | 3
15 | 1
16 |
17 |
18 | 6
> # utilisation de scale
>
> stem(lea$length,scale=2)
The decimal point is 2 digit(s) to the right of the |
0 | 77777888888899999999999999999999999999999999999999999999999999999999
1 | 00000000000000000000000000000000000000000000000111111111111111111111+119
1 | 55555555555555555555555555555555555555555556666666666666666666666666+124
2 | 00000000000000000000000000001111111111111111222222222222223333333333+40
2 | 5555555555555555555556666666666666666666666666777777788888889999999
3 | 00000001111122222333334444444
3 | 5556666788889999
4 | 0011111112223444
4 | 556666777778889
5 | 01224
5 | 55667888
6 | 22344
6 | 588
7 | 234
7 |
8 |
8 | 5
9 |
9 |
10 |
10 |
11 |
11 |
12 | 4
12 |
13 |
13 |
14 | 3
14 |
15 | 1
15 |
16 |
16 |
17 |
17 |
18 |
18 | 6
> # utilisation de width
>
> stem(lea$length,width=130)
The decimal point is 2 digit(s) to the right of the |
0 | 777778888888999999999999999999999999999999999999999999999999999999999999999999
1 | 0000000000000000000000000000000000000000000000011111111111111111111111111111111111111111111122222222222223333333333333+273
2 | 0000000000000000000000000000111111111111111122222222222222333333333333333333333333333333333333333444444444444444444444+57
3 | 000000011111222223333344444445556666788889999
4 | 0011111112223444556666777778889
5 | 0122455667888
6 | 22344588
7 | 234
8 | 5
9 |
10 |
11 |
12 | 4
13 |
14 | 3
15 | 1
16 |
17 |
18 | 6
> # autres exemples
>
> elf <- lit.dar("http://www.info.univ-angers.fr/~gh/Datasets/elf.dar")
> stem(elf$AGE)
The decimal point is 1 digit(s) to the right of the |
1 | 1223455567778889999
2 | 0011222344555566667778888888999
3 | 0011123556799
4 | 0123446778899
5 | 0002239
6 | 0011222345
7 | 033368
> her <- lit.dar("http://www.info.univ-angers.fr/~gh/Datasets/her.dar")
> stem(her$age)
The decimal point is 1 digit(s) to the right of the |
1 | 2677788899
2 | 0000223333455566778889999
3 | 11122222334466777
4 | 00011112455678
5 | 2223345566789
6 |
7 | 3
7. Export de graphiques en PNG et PDF
On veut exporter un graphique en PNG, en PS ou EPS, en PDF. Quelle(s) solution(s) avec R ?
Et avec Rstudio ?
Pour exporter un graphique, il faut utiliser les fonctions du package grDevices et en particulier png(), postscript() et pdf().
pdf(file = ifelse(onefile, "Rplots.pdf", "Rplot%03d.pdf"),
width, height, onefile, family, title, fonts, version,
paper, encoding, bg, fg, pointsize, pagecentre, colormodel,
useDingbats, useKerning, fillOddEven, compress
)
png(filename = "Rplot%03d.png",
width = 480, height = 480, units = "px", pointsize = 12,
bg = "white", res = NA, ...,
type = c("cairo", "cairo-png", "Xlib", "quartz"), antialias
)
postscript(file = ifelse(onefile, "Rplots.ps", "Rplot%03d.ps"),
onefile, family, title, fonts, encoding, bg, fg,
width, height, horizontal, pointsize,
paper, pagecentre, print.it, command,
colormodel, useKerning, fillOddEven
)
Voilà concrètement comment on fait :
-
On ouvre la sortie graphique avec l'une des fonctions citées.
-
On exécute les instructions qui produisent le(s) graphique(s).
-
On ferme le fichier avec dev.off().
Par exemple, pour produire un fichier png correspondant au deux boxplots précédents roses et vert, avec un fichier nommé "demoboxplot.png", de largeur 1400 et de hauteur 100, le code à écrire est :
# Etape préliminaire : disposer des données et tester en interactif les graphiques...
elf <- lit.dar("http://www.info.univ-angers.fr/~gh/Datasets/elf.dar")
ages <- elf$AGE
etud <- factor(elf$ETUD,levels=0:4,labels=c("non réponse","cep","bepc","bac","sup"))
########################################################################
# #
# Etape 1 : définir la sortie graphique #
# #
########################################################################
png(filename="demoboxplot.png",width=1400,height=1000)
########################################################################
# #
# Etape 2 : tracer le(s) graphique(s) #
# #
########################################################################
par(mfrow=c(1,2))
boxplot(
ages~etud,
col="pink",
main="Distribution AGE par niveau d'étude",
sub="(data ELF)\n",
) # fin de boxplot
# avec encoche et largeur proportionnelle à l'effectif
boxplot(
ages~etud,
col="lightgreen",
main="Distribution AGE par niveau d'étude",
sub="(data ELF)\n",
notch=TRUE,
varwidth=TRUE
) # fin de boxplot
par(mfrow=c(1,1))
########################################################################
# #
# Etape 3 : fermer le fichier #
# #
########################################################################
dev.off()
# et voilà !
Le fichier résultat est visible ici.
Remarque : il faut éventuellement changer de chemin d'accès avec setwd() avant de définir le fichier graphique, ou indiquer le chemin d'accès. Par exemple :
###### à la fac, avant les commandes comme png(), pdf()
setwd("D:/") # le / est volontaire car R l'interprète comme \
png("monGraphique.png")
...
dev.off()
# autre solution :
png("D:/monGraphique.png")
...
dev.off()
###### sous Unix, après avoir créé le dossier testGraphiques dans le répertoire courant
setwd("~/testGraphiques/") # car R fait bien "l'expansion du ~"
png("monGraphique.png")
...
dev.off()
# autre solution :
png("~/testGraphiques/monGraphique.png")
...
dev.off()
8. Heatmap, vous avez dit heatmap ?
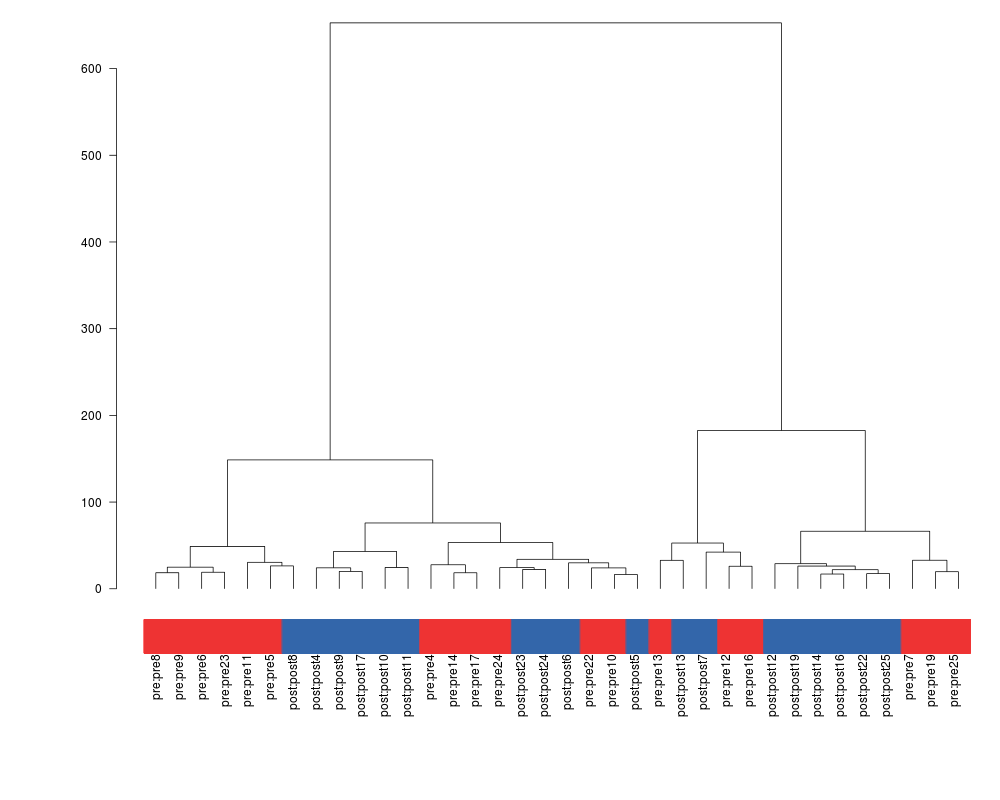
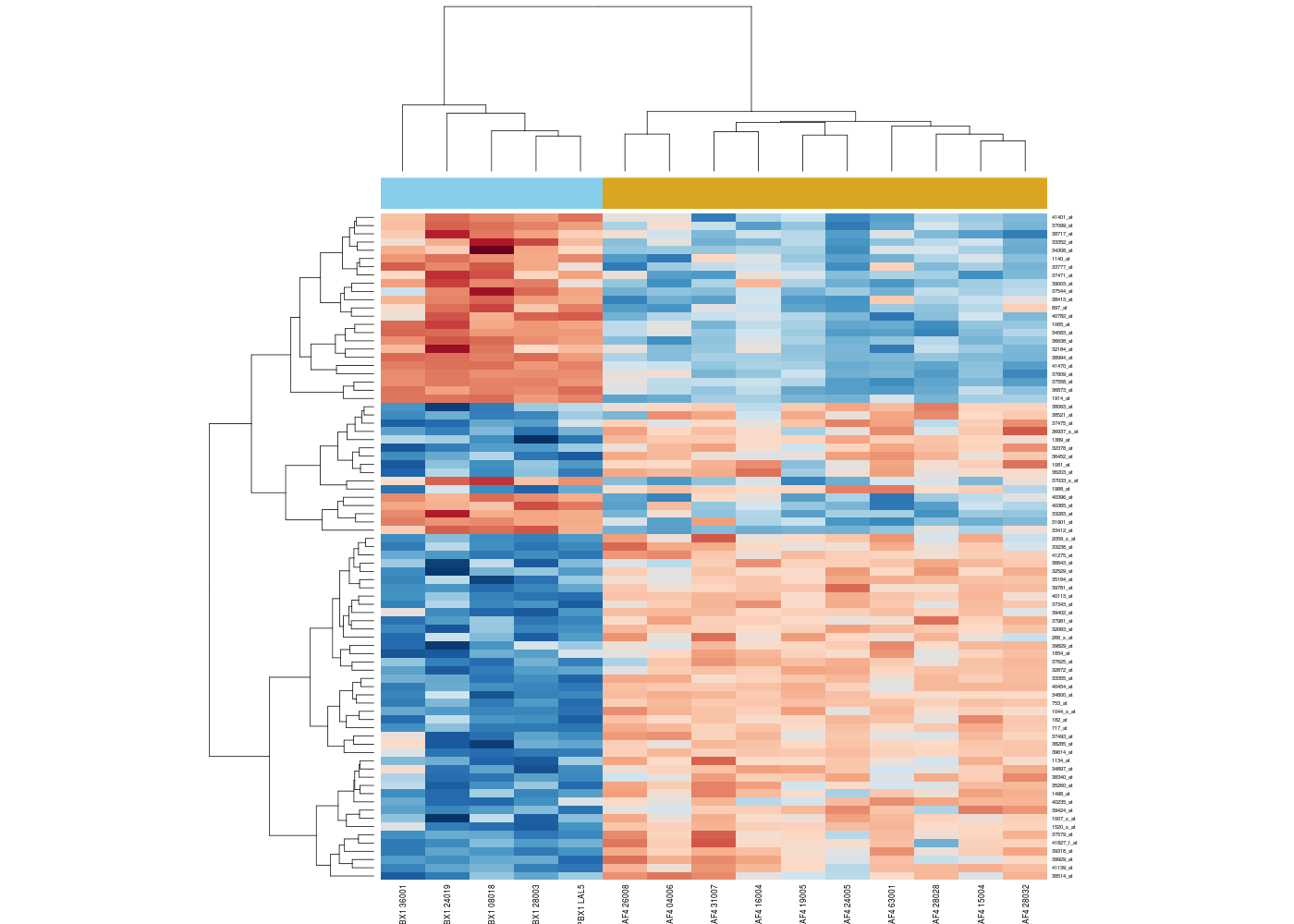
Est-ce facile de tracer des heatmaps améliorées en R avec des dendrogrammes autour comme ci-dessous ?
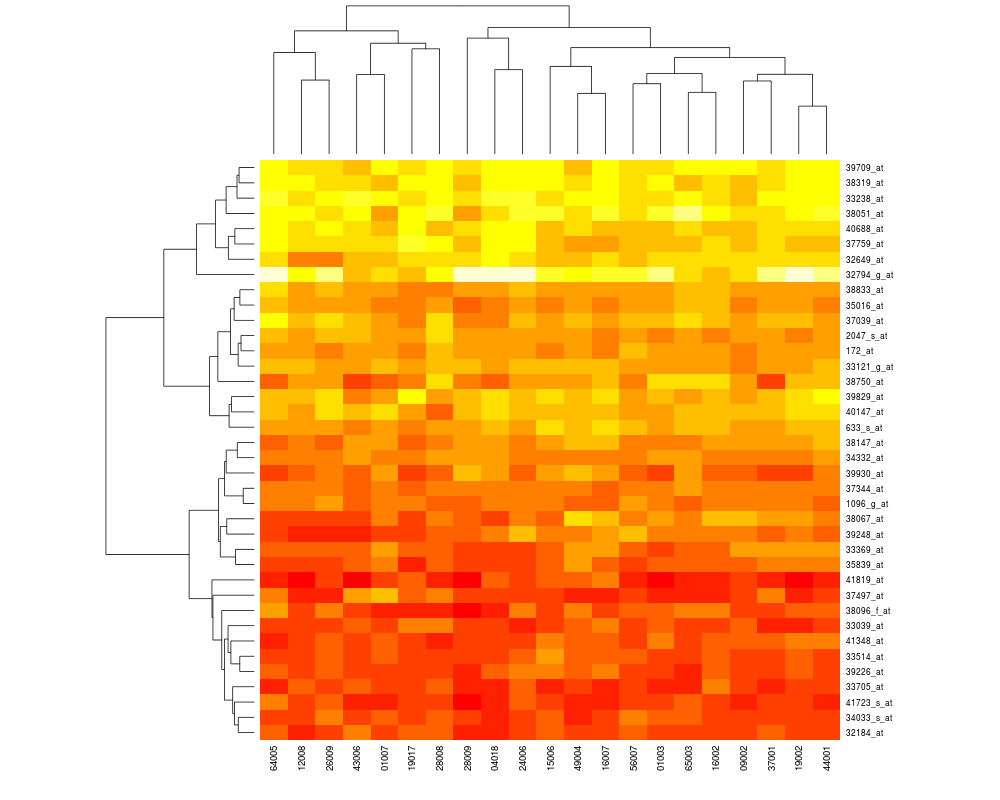
Il n'existe pas une implémentation de la notion de «heatmap améliorée» mais plutôt une bonne dizaine. La consultation de R site search à ce sujet est édifiante : 430 liens en novembre 2013 ! Il y a par exemple la fonction heatmap() du package stats,
la fonction heatmap() du package apcluster,
heatmap() du package GMD,
heatmap()du package gplots,
et enfin (et surtout ?) les fonctions
GO2heatmap et KEGG2heatmap() du package annotate.
La difficuté en général n'est pas le tracé, mais la construction des données. Voici un exemple peu commenté :
library(ALL) # ALL = Acute Lymphoblastic Leukemia
data(ALL) # help(ALL) fournit plus de détails
# on sélectionne les patients dans deux sous-groupes
selSamples <- ALL$mol.biol %in% c("ALL1/AF4","E2A/PBX1")
ALLs <- ALL[,selSamples]
ALLs$mol.biol <- factor(ALLs$mol.biol)
colnames(exprs(ALLs)) <- paste(ALLs$mol.biol,colnames(exprs(ALLs)))
# on ne retient, pour les 15 échantillons et les 12625 sondes,
# que celles dont l'expression moyenne est supérieure à 100
# pour au moins un des deux groupes de patients et une p-value
# du test t à deux échantillons inférieure à 0.0002,
# soit 81 sondes
library(genefilter)
meanThr <- log2(100)
g <- ALLs$mol.biol
s1 <- rowMeans(exprs(ALLs)[ ,g==levels(g)[1] ]) > meanThr
s2 <- rowMeans(exprs(ALLs)[ ,g==levels(g)[2] ]) > meanThr
s3 <- rowttests(ALLs,g)$p.value < 2e-04
slpr <- (s1 | s2) & s3
ALLhm <- ALLs[slpr, ]
library(RColorBrewer)
hmcol <- colorRampPalette(brewer.pal(10,"RdBu"))(256)
spcol <- ifelse(ALLhm$mol.biol=="ALL1/AF4","goldenrod","skyblue")
# et enfin
heatmap(exprs(ALLhm),col=hmcol,ColSideColors=spcol)
Et son résultat :
Malgré un nombre de paramètres très important pour la fonction heatmap() du package stats, l'utilisation en est assez simple, comme on pourra s'en convaincre avec example(heatmap).
> help(heatmap,package="stats")
Draw a Heat Map
===============
Description
-----------
A heat map is a false color image (basically image(t(x))) with a dendrogram added
to the left side and to the top. Typically, reordering of the rows and columns
according to some set of values (row or column means) within the restrictions
imposed by the dendrogram is carried out.
Usage
-----
heatmap(x, Rowv = NULL, Colv = if(symm)"Rowv" else NULL,
distfun = dist, hclustfun = hclust,
reorderfun = function(d, w) reorder(d, w),
add.expr, symm = FALSE, revC = identical(Colv, "Rowv"),
scale = c("row", "column", "none"), na.rm = TRUE,
margins = c(5, 5), ColSideColors, RowSideColors,
cexRow = 0.2 + 1/log10(nr), cexCol = 0.2 + 1/log10(nc),
labRow = NULL, labCol = NULL, main = NULL,
xlab = NULL, ylab = NULL,
keep.dendro = FALSE, verbose = getOption("verbose")
, ...)
La préparation des données et le choix des paramètres de filtrage pour la bioinformatique via R sont assez bien expliqués dans les ouvrages suivants :
Nous vous laissons le soin de lire ces ouvrages pour trouver dans lequel des deux nous avons recopié les instructions pour produire la heatmap améliorée des données ALL.
9. Configuration de R et des graphiques
Comment configurer R en général ? Et pour les graphiques ? Où mettre des options courantes de R ? Quelles sont ces options ?
Si on dit .Rprofile.site et .Rprofile, tout est dit !
Le fichier .Rprofile est un fichier texte qui contient du code R que R consulte automatiquement. Il peut y en avoir un pour l'utilisateur (configuration générale) et un dans le sous-répertoire courant (configuration spécialisée). De plus R permet de définir des fonctions .First() et .Last() bien utiles, par exemple pour afficher un message de bienvenue, ou pour sauvegarder de façon incrémentale tout le travail effectué. Voici quelques liens pour approfondir cette notion de profil :
Comme déjà dit plus haut, les options générales se gèrent via la fonction options() du package base et les options graphiques avec la fonction par() du package graphics.
10. Non présentation (!) des packages graphics, beanplot, lattice, grid, plotrix et ggplot2.
Que contiennent les packages graphics, beanplot, lattice, grid, plotrix et ggplot2 ?
Quelles en sont les fonctions les plus importantes ?
A part pour beanplot, il est illusoire de vouloir présenter ces packages en peu de temps donc à moins d'y passer une bonne dizaine d'heures, il est difficile de connaitre ces packages. Le tableau suivant indique le nombre d'objets dans chaque package et fournit des liens vers la liste des objets de ces packages.
11. Bibliographie des graphiques en R
Y a-t-il beaucoup de livres sur les graphiques en R ?
Oui et non !
En fait, la plupart des livres qui traitent de R présentent au passage les graphiques de R. Il n'y a par contre que quelques ouvrages spécialisés sur les graphiques en R ou les packages graphiques de R (moins d'une vingtaine en tout, en novembre 2013). En voici une sélection personnelle :
Remarque :
Tous les graphiques de l'ouvrage R Graphics (Second Edition) de Paul Murrell, publié en 2011, sont visibles,
avec le code R associé pour les reproduire, à l'adresse RG2e.
En particulier le chapitre 4 présente les graphiques générés avec le package lattice et le chapitre 5 présente les graphiques générés avec le package ggplot2.
Code-source php de cette page ; code javascript utilisé. Retour à la page principale du cours.
|
 Retour à la page principale de
(gH)
Retour à la page principale de
(gH)