Statistiques élémentaires avec le logiciel R
|
-- Session de formation continue pour l'université d'Angers --
|
Séance 4 : Analyse élémentaire de données quantitatives
|
1. Calculs et représentations graphiques pour les QT en dimension 1 et 2
Rappel : réaliser la description d'une seule variable ou de plusieurs variables séparément, c'est effectuer une analyse univariée alors que les traiter deux à deux se nomme analyse bivariée. Enfin, une analyse multivariée prend toutes les variables en compte en même temps.
1.1 Comment décrire une seule QT ?
Pour décrire une seule variable QT, on distingue les calculs toujours possibles, comme les quantiles ou percentiles tels la médiane, les quartiles, de ceux supposant une additivité des données, nommés moyenne, variance, écart-type, coefficient de variation. Il est souvent conseillé d'utiliser la médiane plutôt que la moyenne lorsque les données sont réparties sur plusieurs ordres de grandeur. Ces deux indicateurs permettent d'appréhender le centre ou la tendance centrale des données alors que l'écart-type et l'écart inter-quartiles viennent décrire la dispersion absolue des données tandis que la dispersion relative s'exprime par le coefficient de variation ou l'écart inter-quartiles relatif.
On peut aussi trier les données, les afficher en tige-et-feuilles (stem and leaf en anglais) pour comprendre comment elles sont distribuées, les découper en classes. Au niveau des représentations graphiques, on préfère tracer les valeurs quand elles sont peu nombreuses (disons jusqu'à une centaine) mais il est courant d'utiliser un histogramme des classes avec une approximation par densité au-delà. Il est parfois utile d'y superposer la courbe de la loi normale associée, de donner l'intervalle de confiance de la moyenne à 95 %, d'en tracer aussi la boite à moustaches avec ou sans encoche...
Attention : si on calcule et affiche le minimum et le maximum d'une variable QT, on ne s'en sert pas au niveau statistique parce que ce ne sont pas des résumés globaux, mais plutôt des indicateurs locaux, étant donné qu'une seule valeur peut suffire à modifier ces extrema. Ces minima et ces maxima servent principalement à vérifier la plage de variation des données.
Les principales fonctions de R associées à ces calculs et représentations se nomment summary(), mean(), sd(), quantile(), median(), plot(), hist() et boxplot().
Exemple de code-source R pour traiter la variable AGE des données ROSSO, fichier rosso_mini3.dar :
## indicateurs numériques d'une variable QT
## exemple : l'AGE dans les données rosso_mini3.dar
# lecture et affichage des données
rosso <- read.table("rosso_mini3.dar",head=TRUE,row.names=1,dec=",")
print(rosso$AGE)
# les résumés fournis par R
print(summary(rosso$AGE))
# et l'écart-type ?
cat("l'écart-type est :",sd(rosso$AGE),"ans\n")
# pour la distribution des données :
print(quantile(rosso$AGE))
print(stem(rosso$AGE))
# un tracé en points, un histogramme et un boxplot
par(mfrow=c(1,3))
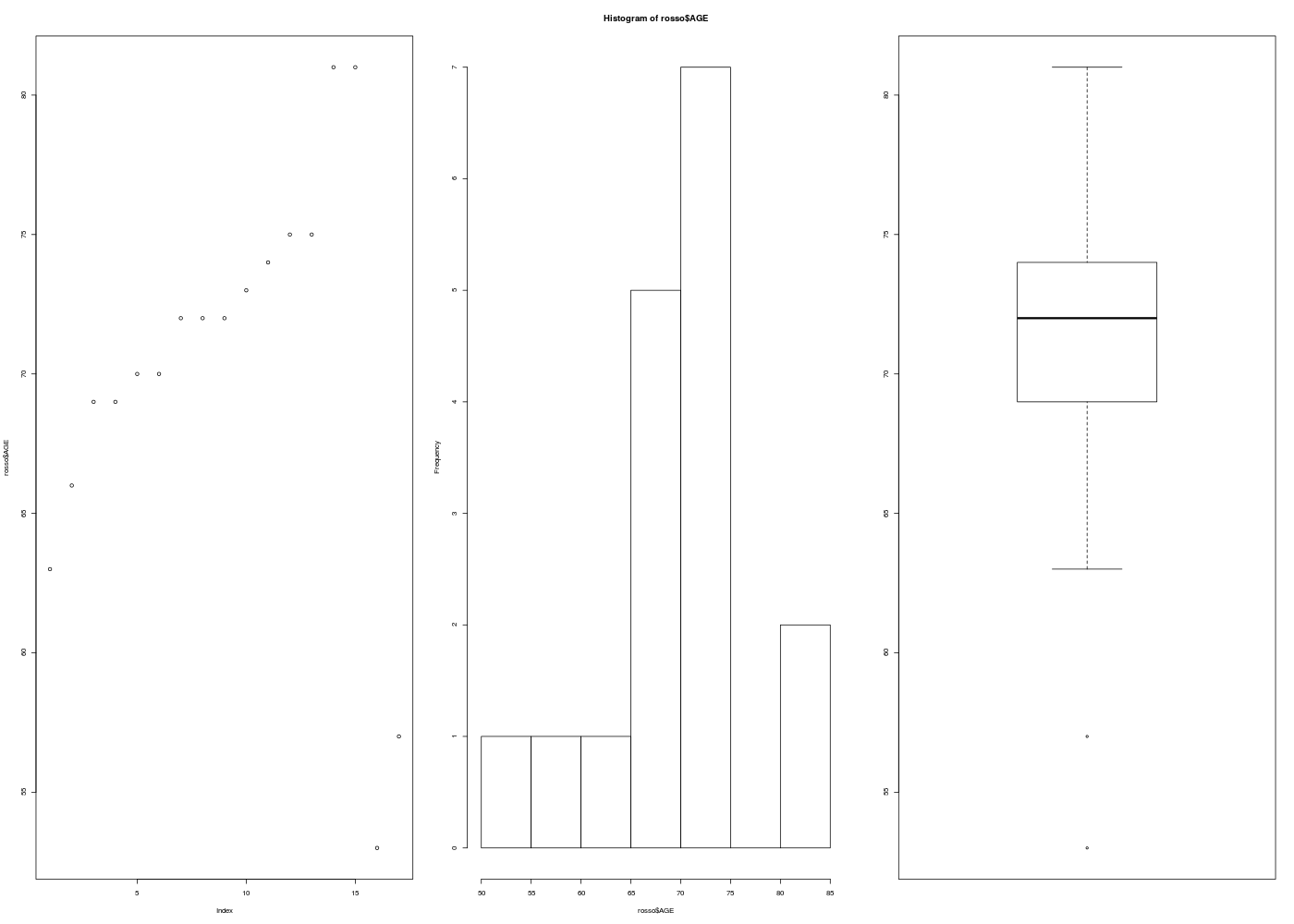
plot(rosso$AGE)
hist(rosso$AGE)
boxplot(rosso$AGE)
par(mfrow=c(1,1))
Résultats :
[1] 63 66 69 69 70 70 72 72 72 73 74 75 75 81 81 53 57
Min. 1st Qu. Median Mean 3rd Qu. Max.
53.00 69.00 72.00 70.12 74.00 81.00
l'écart-type est : 7.304813 ans
0% 25% 50% 75% 100%
53 69 72 74 81
The decimal point is 1 digit(s) to the right of the |
5 | 37
6 | 3699
7 | 002223455
8 | 11
Graphiques générés :
Il est clair que R fournit les fonctions pour réaliser les calculs et les graphiques, mais c'est un peu minimaliste... Nous verrons un peu plus loin comment obtenir de "beaux" affichages.
1.2 Comment décrire plusieurs QT ?
Pour décrire plusieurs variables QT séparément, on regroupe les indicateurs précédents (moyenne, médiane, écart-type, coefficient de variation...) dans un tableau résumé à raison d'une variable par ligne ou par colonne. Il est conseillé de fournir plusieurs affichages triés suivant différents critères : par ordre alphabétique des variables (si elles sont nombreuses), par coefficient de variation décroissant (si les unités sont différentes), par moyenne décroissante (si ce sont les mêmes unités)...
Exemple de code-source R pour traiter toutes les variables QT du dossier ROSSO, fichier rosso_mini3.dar :
## indicateurs numériques d'une variable QT
## exemple : toutes les QT dans les données rosso_mini
# lecture et affichage des données
rosso <- read.table("rosso_mini3.dar",head=TRUE,row.names=1,dec=",")
rossoQT <- rosso[,-(2:3)]
# résumés numériques (sans tri ni aménagement)
summary(rossoQT)
Résultats :
AGE L30 Htrr MLD Baddeley PASAT
Min. :53.00 Min. :14.00 Min. : 0.00 Min. :-2.0 Min. : 69.47 Min. :21.00
1st Qu.:69.00 1st Qu.:18.00 1st Qu.: 7.00 1st Qu.: 2.0 1st Qu.: 89.66 1st Qu.:40.00
Median :72.00 Median :21.00 Median :16.00 Median : 3.5 Median : 97.06 Median :50.00
Mean :70.12 Mean :20.82 Mean :13.47 Mean : 3.0 Mean : 95.17 Mean :47.06
3rd Qu.:74.00 3rd Qu.:24.00 3rd Qu.:20.00 3rd Qu.: 4.0 3rd Qu.:101.97 3rd Qu.:57.00
Max. :81.00 Max. :28.00 Max. :20.00 Max. : 6.0 Max. :112.47 Max. :60.00
Par contre pour les décrire conjointement, c'est-à-dire ensemble deux à deux, on calcule pour chaque couple de variables QT un coefficient de corrélation, le plus souvent celui de la corrélation linéaire au sens de Pearson, et on présente l'ensemble de ces coefficients sous forme d'une matrice, nommée mdc ou, selon l'usage, « matrice de corrélation », là où il faudrait dire matrice des coefficients de corrélation [linéaire]. Il faut ensuite trier ces coefficients par valeur absolue décroissante avant de fournir éventuellement les coefficients du modèle linéaire sous-jacent. Il est conseillé de produire une grille ou mosaique des tracés deux à deux ou scatterplot afin de visualiser la distribution des différents couples de points.
Exemple de code-source R pour les données QT du dossier ROSSO, fichier rosso_mini3.dar :
## indicateurs numériques d'une variable QT
## exemple : toutes les QT dans les données rosso_mini
# lecture et affichage des données
rosso <- read.table("rosso_mini3.dar",head=TRUE,row.names=1,dec=",")
rossoQT <- rosso[,-(2:3)]
# matrice des coefficients de corrélation linéaire (au sens de Pearson)
cat("\nCorrélation \"classique\"\n\n")
print(cor(rossoQT))
# matrice dess coefficients de corrélation des rangs (Spearman)
cat("\nCorrélation des rangs\n\n")
print(round(cor(rossoQT,method="spearman"),3))
# graphique en paires
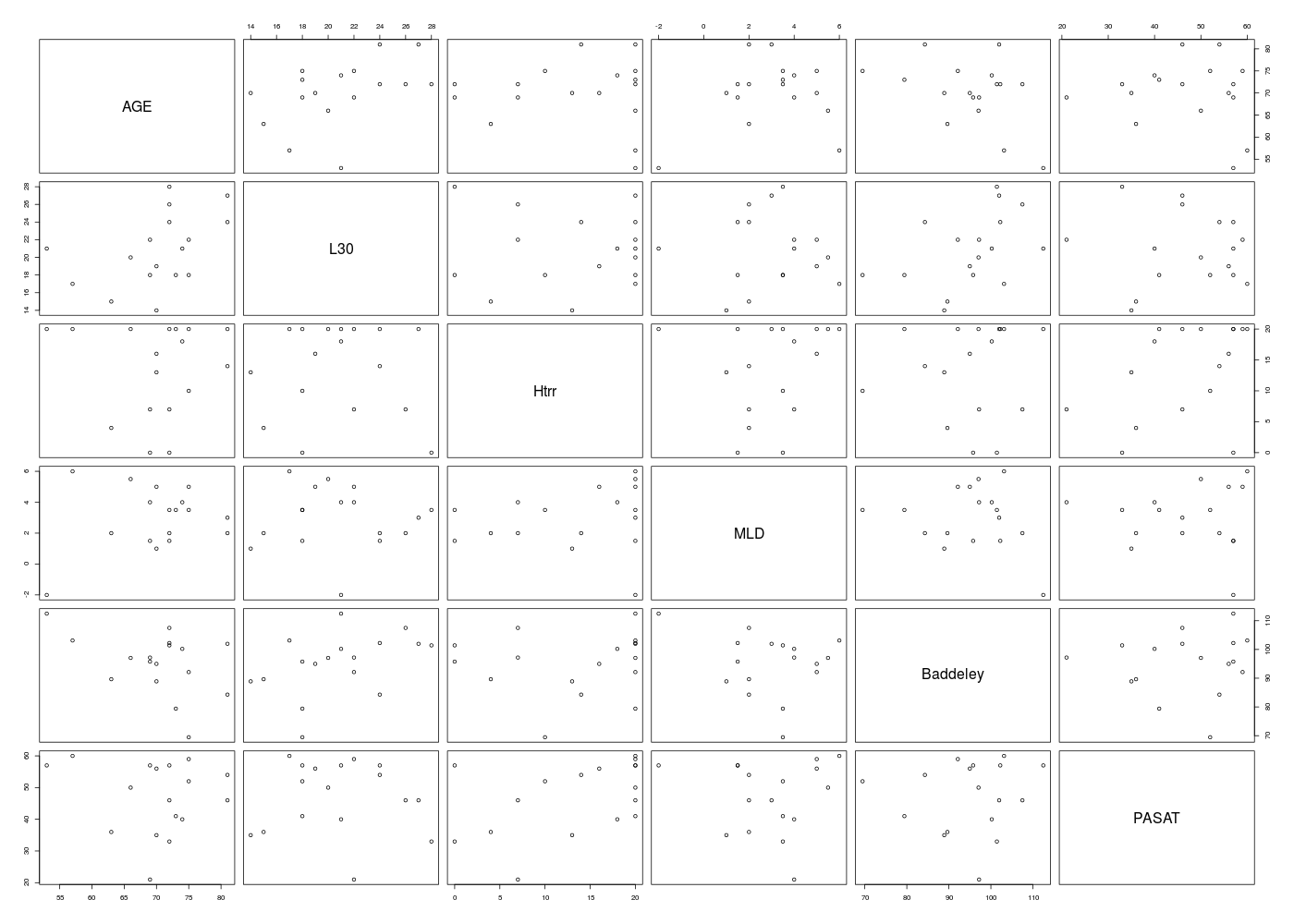
pairs(rossoQT)
Résultats :
Corrélation "classique"
AGE L30 Htrr MLD Baddeley PASAT
AGE 1.00000000 0.44436431 -0.03697155 0.201300033 -0.43158859 -0.124800030
L30 0.44436431 1.00000000 -0.02627909 -0.023422914 0.43763560 -0.030113935
Htrr -0.03697155 -0.02627909 1.00000000 0.175400037 0.09656126 0.441195854
MLD 0.20130003 -0.02342291 0.17540004 1.000000000 -0.20874280 -0.008483286
Baddeley -0.43158859 0.43763560 0.09656126 -0.208742802 1.00000000 0.080360042
PASAT -0.12480003 -0.03011393 0.44119585 -0.008483286 0.08036004 1.000000000
Corrélation des rangs
AGE L30 Htrr MLD Baddeley PASAT
AGE 1.000 0.474 0.087 0.038 -0.357 -0.078
L30 0.474 1.000 0.039 -0.025 0.466 -0.072
Htrr 0.087 0.039 1.000 0.261 0.203 0.493
MLD 0.038 -0.025 0.261 1.000 -0.067 0.074
Baddeley -0.357 0.466 0.203 -0.067 1.000 0.193
PASAT -0.078 -0.072 0.493 0.074 0.193 1.000
Graphique généré :
Là encore, il est clair que R fournit "juste" des fonctions pour réaliser les calculs et les graphiques, qu'il faut les enrichir pour obtenir de "beaux" affichages et "beaux" graphiques.
2. Etude de cas : manipulations avec R sous Rstudio
2.1 Analyse univariée
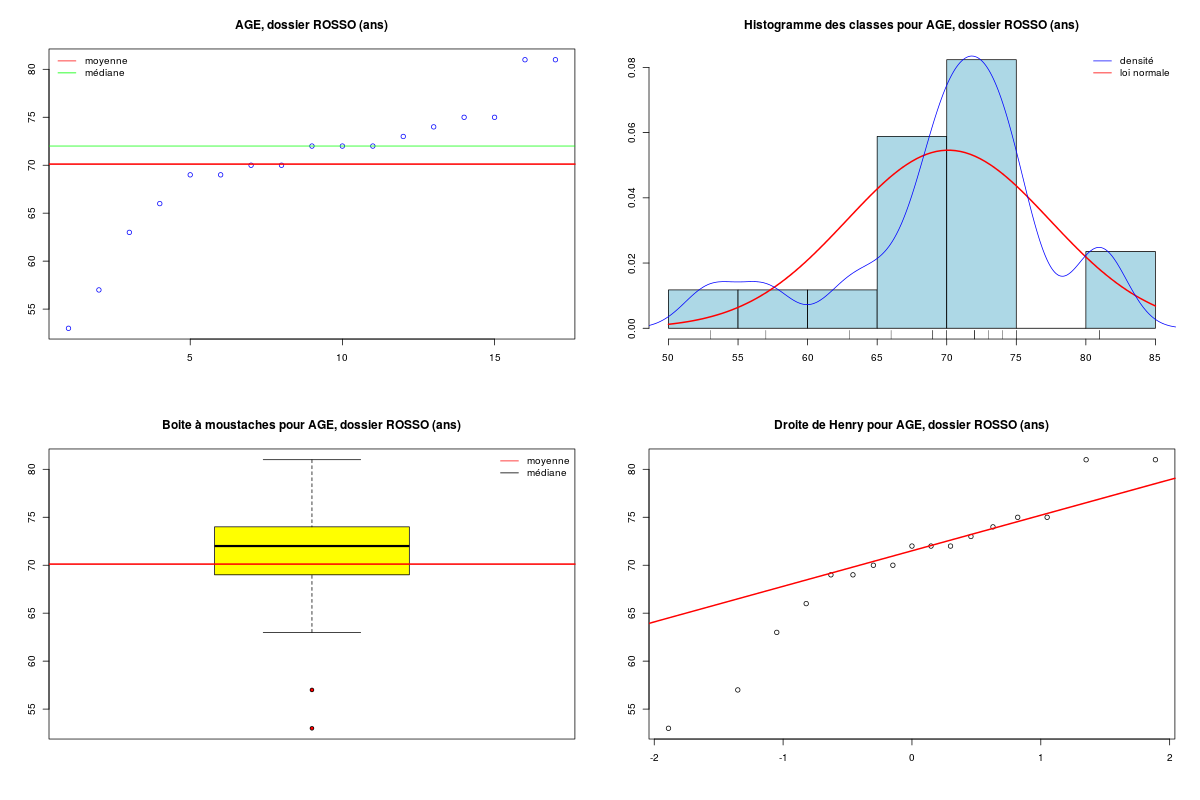
Pour analyser et représenter graphiquement une seule variable, il est conseillé d'être exhaustif, quitte à ne retenir dans la rédaction que les éléments les plus marquants. Nous fournissons une fonction nommée decriQT dont le but est de bien présenter tous les résultats. En voici la démonstration pour la variable AGE des données ROSSO, fichier rosso_mini3.dar :
DESCRIPTION STATISTIQUE DE LA VARIABLE AGE (dossier ROSSO)
Taille 17 individus
Moyenne 70.1176 ans
Ecart-type 7.3048 ans
Coef. de variation 10 %
1er Quartile 69.0000 ans
Mediane 72.0000 ans
3eme Quartile 74.0000 ans
iqr absolu 5.0000 ans
iqr relatif 7.0000 %
Minimum 53.000 ans
Maximum 81.000 ans
Tracé tige et feuilles
The decimal point is 1 digit(s) to the right of the |
5 | 37
6 | 3699
7 | 002223455
8 | 11
Graphique généré :
De la même façon, pour obtenir un tableau synthétique des résumés de l'ensemble des variables, nous avons conçu la fonction nommée allQTdf dont le but est de bien présenter et de trier tous les résultats. En voici la démonstration pour les données ROSSO, fichier rosso_mini3.dar :
Description des 6 variables statistiques par cdv décroissant
Num Nom Taille Moyenne Unite Ecart-type Coef. de var. Minimum Maximum
4 MLD 17 3.000 ? 1.976 65.88 % -2.000 6.000
3 Htrr 17 13.471 ? 7.392 54.87 % 0.000 20.000
6 PASAT 17 47.059 ? 11.183 23.76 % 21.000 60.000
2 L30 17 20.824 ? 4.050 19.45 % 14.000 28.000
5 Baddeley 17 95.169 ? 10.574 11.11 % 69.470 112.470
1 AGE 17 70.118 ? 7.305 10.42 % 53.000 81.000
Par ordre d'entrée
Num Nom Taille Moyenne Unite Ecart-type Coef. de var. Minimum Maximum
1 AGE 17 70.118 ? 7.305 10.42 % 53.000 81.000
2 L30 17 20.824 ? 4.050 19.45 % 14.000 28.000
3 Htrr 17 13.471 ? 7.392 54.87 % 0.000 20.000
4 MLD 17 3.000 ? 1.976 65.88 % -2.000 6.000
5 Baddeley 17 95.169 ? 10.574 11.11 % 69.470 112.470
6 PASAT 17 47.059 ? 11.183 23.76 % 21.000 60.000
2.2 Analyse bivariée
Une vraie analyse bivariée se doit d'analyser les coefficients de corrélation. C'est le but de notre fonction allQT :
Matrice des corrélations au sens de Pearson pour 17 lignes et 6 colonnes
AGE L30 Htrr MLD Baddeley PASAT
AGE 1.000
L30 0.444 1.000
Htrr -0.037 -0.026 1.000
MLD 0.201 -0.023 0.175 1.000
Baddeley -0.432 0.438 0.097 -0.209 1.000
PASAT -0.125 -0.030 0.441 -0.008 0.080 1.000
Meilleure corrélation 0.4443643 pour L30 et AGE p-value 0.0739
Formules AGE = 0.801 * L30 + 53.429
et L30 = 0.246 * AGE + 3.548
Coefficients de corrélation par ordre décroissant
0.444 p-value 0.0739 pour L30 et AGE : L30 = 0.246 x AGE + 3.548
0.441 p-value 0.0763 pour PASAT et Htrr : PASAT = 0.667 x Htrr + 38.068
0.438 p-value 0.0789 pour Baddeley et L30 : Baddeley = 1.143 x L30 + 71.377
-0.432 p-value 0.0837 pour Baddeley et AGE : Baddeley = -0.625 x AGE + 138.975
-0.209 p-value 0.4214 pour Baddeley et MLD : Baddeley = -1.117 x MLD + 98.519
0.201 p-value 0.4385 pour MLD et AGE : MLD = 0.054 x AGE - 0.819
0.175 p-value 0.5007 pour MLD et Htrr : MLD = 0.047 x Htrr + 2.368
-0.125 p-value 0.6332 pour PASAT et AGE : PASAT = -0.191 x AGE + 60.455
0.097 p-value 0.7124 pour Baddeley et Htrr : Baddeley = 0.138 x Htrr + 93.308
0.080 p-value 0.7592 pour PASAT et Baddeley : PASAT = 0.085 x Baddeley + 38.971
-0.037 p-value 0.8880 pour Htrr et AGE : Htrr = -0.037 x AGE + 16.094
-0.030 p-value 0.9087 pour PASAT et L30 : PASAT = -0.083 x L30 + 48.790
-0.026 p-value 0.9203 pour Htrr et L30 : Htrr = -0.048 x L30 + 14.469
-0.023 p-value 0.9289 pour MLD et L30 : MLD = -0.011 x L30 + 3.238
-0.008 p-value 0.9742 pour PASAT et MLD : PASAT = -0.048 x MLD + 47.203
3. Etude de cas : manipulations avec Rcommander
3.1 Analyse univariée
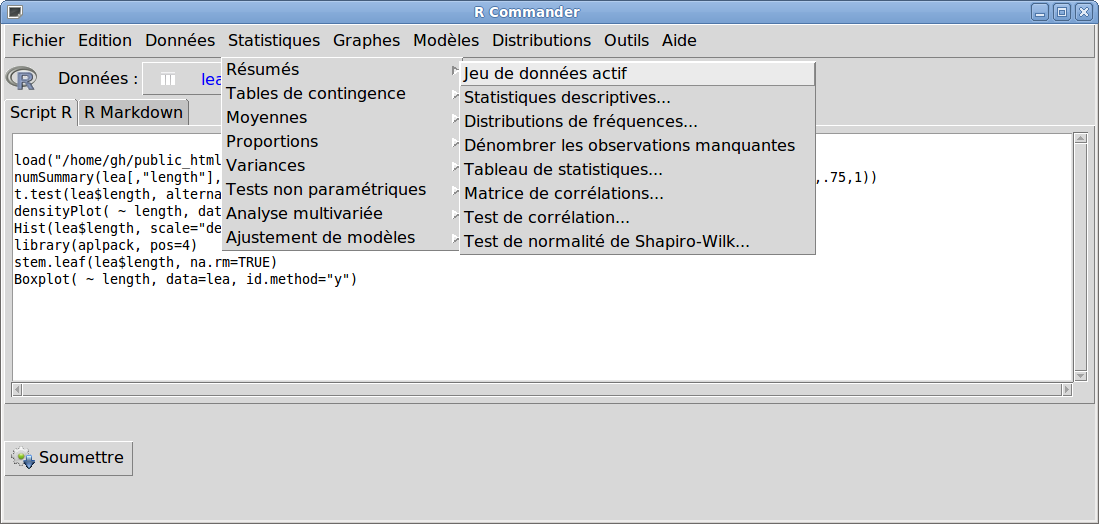
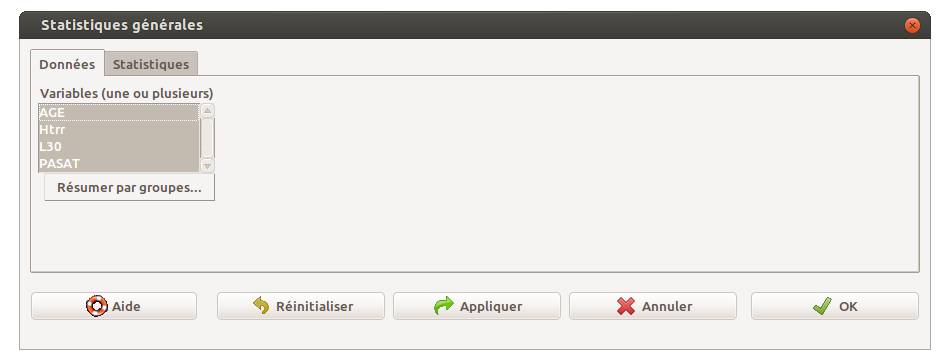
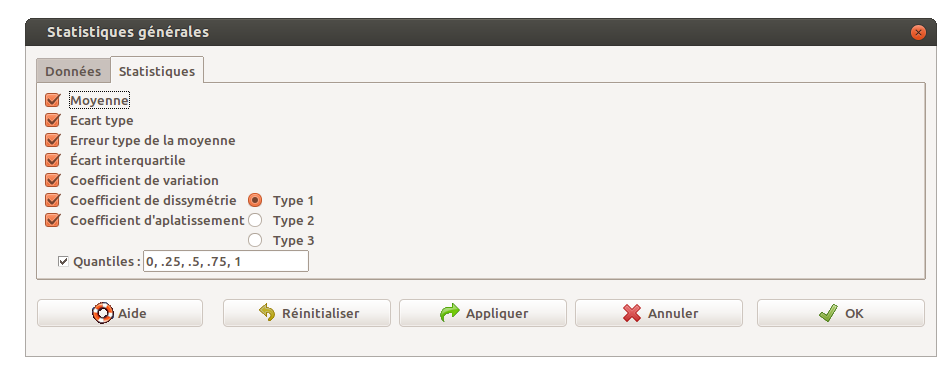
Il est très simple de traiter des données QT avec Rcmdr car on dispose du menu Statistiques, sous-menu Résumés, sous-sous-menu Statistiques descriptives. Il est alors possible de choisir plusieurs variables (en cliquant sur la touche CTRL) et l'onglet Statistiques permet de choisir quels calculs on veut effectuer. On notera que les affichages des résultats sont en anglais, comme ci-dessous alors que les menus sont en français :
Rcmdr> numSummary(rosso[,c("AGE", "Htrr", "L30", "PASAT")],
statistics=c("mean", "sd", "se(mean)", "IQR", "quantiles",
"cv", "skewness", "kurtosis"), quantiles=c(0,.25,.5,.75,1),
type="1")
mean sd se(mean) IQR cv skewness kurtosis 0% 25% 50% 75% 100% n
AGE 70.11765 7.304813 1.7716774 5 0.1041794 -0.7922402 0.4480431 53 69 72 74 81 17
Htrr 13.47059 7.391868 1.7927912 13 0.5487413 -0.6801391 -0.9818115 0 7 16 20 20 17
L30 20.82353 4.050236 0.9823265 6 0.1945029 0.1610046 -0.8365536 14 18 21 24 28 17
PASAT 47.05882 11.182970 2.7122687 17 0.2376381 -0.7436817 -0.3369492 21 40 50 57 60 17
RcmdrMsg: [3] AVIS: Warning in cv(X) : not all values are positive
3.2 Analyse bivariée
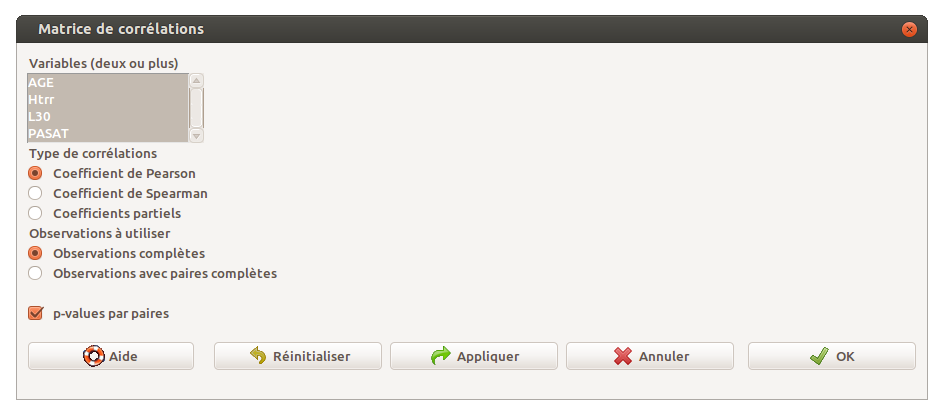
Pour les corrélations, il faut passer par le sous-sous-menu Matrice de corrélations du sous-menu Résumés du menu Statistiques :
Rcmdr> rcorr.adjust(rosso[,c("AGE","Htrr","L30","PASAT")], type="pearson", use="complete")
Pearson correlations:
AGE Htrr L30 PASAT
AGE 1.0000 -0.0370 0.4444 -0.1248
Htrr -0.0370 1.0000 -0.0263 0.4412
L30 0.4444 -0.0263 1.0000 -0.0301
PASAT -0.1248 0.4412 -0.0301 1.0000
Number of observations: 17
Pairwise two-sided p-values:
AGE Htrr L30 PASAT
AGE 0.8880 0.0739 0.6332
Htrr 0.8880 0.9203 0.0763
L30 0.0739 0.9203 0.9087
PASAT 0.6332 0.0763 0.9087
Adjusted p-values (Holm's method)
AGE Htrr L30 PASAT
AGE 1.0000 0.4436 1.0000
Htrr 1.0000 1.0000 0.4436
L30 0.4436 1.0000 1.0000
PASAT 1.0000 0.4436 1.0000
4. Mise en forme des résultats et interprétation
C'est une chose que de calculer, c'en est une autre que de savoir présenter et interpréter. Bien souvent il faut reprendre les affichages de sortie pour choisir le nombre de décimales afin de bien rendre visibles les "meilleures" moyennes ou les coefficients de variation. Il faut ensuite choisir le ou les graphiques que l'on considère comme représentatifs de l'ensemble de la situation et tout cela demande du temps.
Au niveau de la rédaction, puisque les «les variables varient», il faut trouver les termes les plus adaptés pour décrire cette variabilité, parmi des adjectifs comme : dispersé, hétérogène, sélectif, forcé, marqué, influencé... Il faut ensuite se souvenir que les moyennes et les écart-types (ou les coefficients de variation) ne disent pas la même chose : les premiers donnent la tendance et les seconds la dispersion autour de la tendance. Par exemple pour des tests (d'audition, de compréhension, de perception...) les moyennes expriment l'ensemble des résultats (test globalement bien réussi, bien compris, par exemple si la moyenne est haute) alors que le coefficient de variation révèle les écarts à cette moyenne (test réussi par tous ou seulement en moyenne...).
5. Les points essentiels à retenir
-
Avant de commencer l'analyse des QT, il faut s'assurer que l'on maîtrise le sens des unités et qu'on a vérifié les plages de variation afin de ne pas avoir de données aberrantes.
-
On distingue les résumés de tendance centrale (moyenne, médiane) des résumés de dispersion absolue (écart-type, iqr) et des résumés de dispersion relative (coefficient de variation, iqr relatif).
-
Il est d'usage d'ordonner les résultats (par coefficient de variation, par médiane...) selon la nature des données.
-
On double en général les tableaux de résultats de représentations graphiques comme les histogrammes de classes, les courbes de densité et les boites à moustaches.
-
Un tracé graphique par paires fournit souvent une vision globale intéressante de l'ensemble des variables QT.
-
L'analyse des coefficients de corrélation est souvent longue et parfois ingrate.
exercices : énoncés solutions liens : lexique des fonctions vues retour au plan de cours
|
 Retour à la page principale de
(gH)
Retour à la page principale de
(gH)