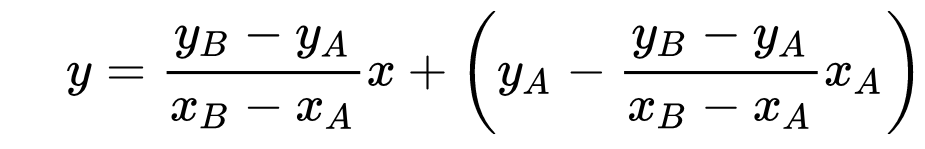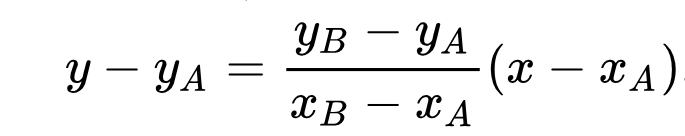Un peu de géométrie
Mathématiques CRPE, La Rochelle, 2020
gilles.hunault "at" univ-angers.fr
1. Le vocabulaire de la géométrie du plan euclidien traditionnel
Pour les jeunes enfants, la géométrie se limite à reconnaitre des formes (carré, cercle, triangle...). Associée à des couleurs, elle permet le dénombrement, le groupement, la sériation. A l'aide d'objets réels en plastique ou en bois, il est possible de réaliser des opérations arithmétiques et des démonstrations géométriques intéressantes. Ainsi, il existe une démonstration visuelle de la formule du carré d'une somme basée sur des carrés et des rectangles, on peut expliciter les fractions avec des rangées de cubes...
La géométrie grecque traditionnelle, celle des espaces et des figures, a été complétée par la géométrique cartésienne avec ses coordonnées et ses équations. On lira donc avec attention la rubrique du Wiki français nommée
et sa page connexe nommée fraction avant d'aborder les formules pour les droites et les distances, comme celles indiquées dans la rubrique du Wiki français nommée
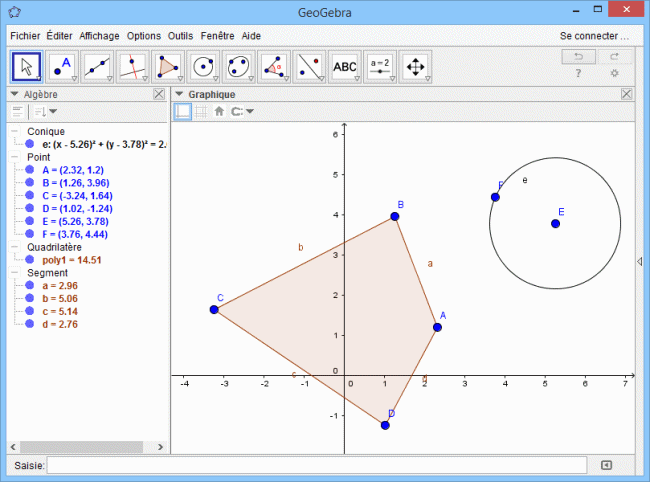
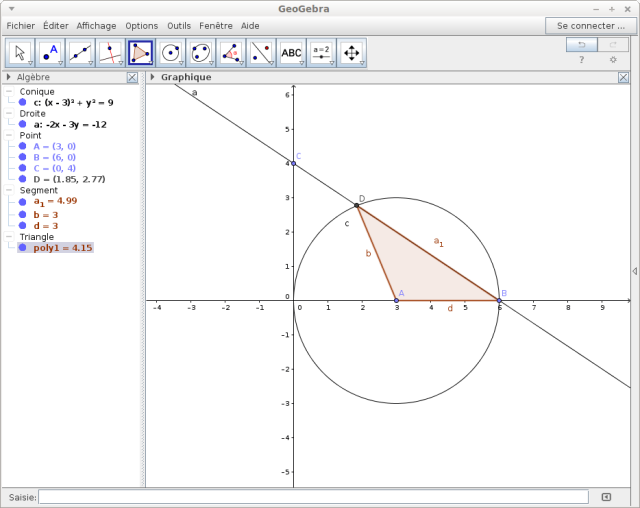
Le fait de disposer de formules permet le calcul informatique des distances, des équations. Ainsi le logiciel geogebra et sa page graphing tracent et calculent dans un navigateur tout ce qu'il faut pour la classe de troisième et au-delà.
Le vocabulaire de base de la géométrie se compose de noms associés à des objets comme les points, les segments, les droites et d'adjectifs associés à des propriétés comme perpendiculaire, égal, symétrique. Les objets peuvent être plus ou moins complexes, comme les droites, les triangles, les polygones et en particulier les polygones réguliers étoilés.
Le document Rappel de géométrie plane de Monsieur Paul MILAN devrait suffire à vous remémorer ce vocabulaire (copie locale).
On n'oubliera pas que la géométrie demande des notions fines de motricité, de latéralisation et d'attention.
Par exemple il est fréquent pour les jeunes apprenant(e)s de ne pas faire attention à la place du signe dans une définition de point comme $M(1,-2)$ ou de confondre $(1,2)$ avec $(2,1)$ au niveau du tracé.
2. Démonstrations géométriques
Il y a en gros deux types de démonstrations géométriques : celles qui sont calculatoires (ou au moins basées sur la calcul) et celles qui sont déductives.
Deux théorèmes de géométrie jouent à cet égard un role fondamental :
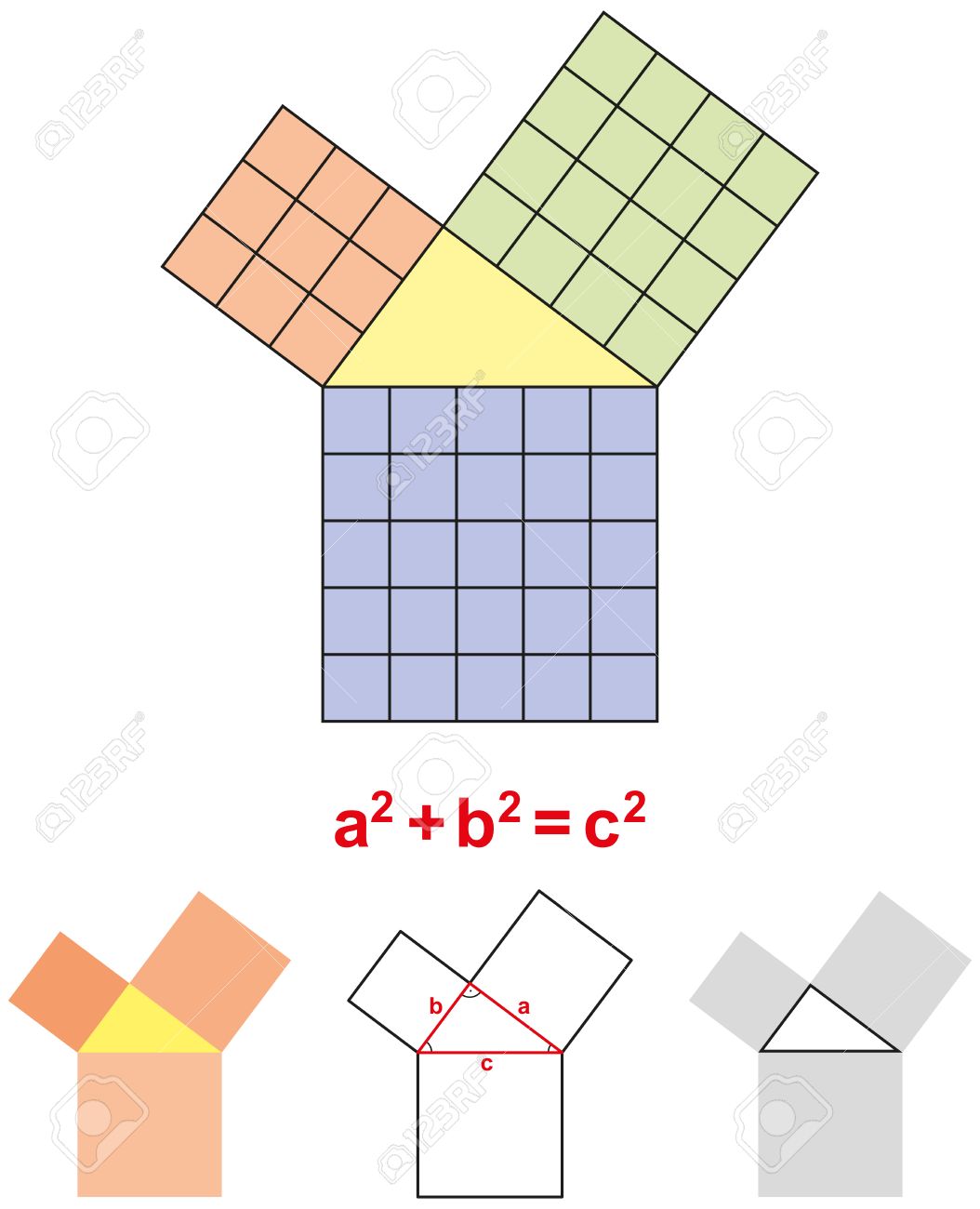
Ainsi, le théorème de Pythagore permet d'inférer que le triangle dont les cotés valent respectivement 3, 4 et 5 est un triangle rectangle parce qu'on a : 52 = 32 + 42.
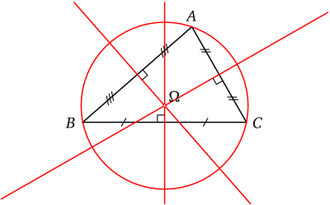
Un autre exemple : un triangle inscrit dans un demi-cercle est rectangle. Si on montre que les trois points qui définissent le triangle sont sur un cercle et qu'un des cotés est un diamètre, alors le triangle est rectangle sans qu'on ait à calculer quoi que ce soit.
Il va de soi qu'un argument comme « on voit sur la figure » n'est pas une démonstration. De plus, comme le montrent les paradoxes géométriques en section 4 de cette page, les illusions visuelles incitent à ne pas croire ce que l'on voit.
3. Un peu de pratique du calcul géométrique
Problème numéro 1 :
Rappeler comment on obtient géométriquement $\sqrt{2}$ .
Démontrer que $\sqrt{2}$ ne peut pas être un nombre entier.
Démontrer que $\sqrt{2}$ ne peut pas être un nombre rationnel. On pourra se servir de l'équivalence $n\ pair\ \iff\ n^2\ pair$ .
solution
$\sqrt{2}$ s'interprète comme la diagonale d'un carré de coté $1$ .
Pour démontrer que $\sqrt{2}$ ne peut pas être un nombre entier, il suffit de passer en revue les nombres entiers.
$0^2=0<2$ donc $\sqrt{2}$ ne peut pas être égal à 0.
$1^2=1<2$ donc $\sqrt{2}$ ne peut pas être égal à 1.
$2^2=4>2$ donc $\sqrt{2}$ ne peut pas être égal à 2. Comme on a dépassé $ 2$ on a testé tous les entiers possibles. Aucun ne convient. Donc $\sqrt{2}$ ne peut pas être un nombre entier.
On suppose maintenant que $\sqrt{2}=a/b$ où $a/b$ est une fraction irréductible et nous allons montrer que cela aboutit à une contradiction.
Si $\sqrt{2}=a/b$ alors $2=a^2/b^2$ soit encore $a^2=2b^2$ donc $ a$ est pair.
On écrit donc $a=2k$ d'où $a^2=4k^2=2b^2$ soit encore $b^2=2k^2$ donc $ b$ est pair : $b=2p$ .
Nous avons donc la contradiction souhaitée : on avait supposé $a/b$ irréductible mais nous venons de montrer que $a/b$=2k/2p est réductible par $ 2$ .
Problème numéro 2 :
On considère dans le plan 4 points $ A$ , $ B$ , $ I$ et $ Z$ tels que
Tracer les droites. On mettra $ I$ avant $ Z$ , $ A$ avant $ B$ , $ I$ au-dessus de $ A$ , $ Z$ au-dessus de $ B$ , $ Z$ au-dessus de $ I$ et $ B$ au-dessous de $ A$ ,
On nomme $ R$ le point de rencontre de $ (AB)$ et $ (IZ)$ . $ R$ sera donc à gauche de $ I$ et $ A$ .
Enoncer les relations issues du théorème de Thalès à l'aide de $ R$ .
solution
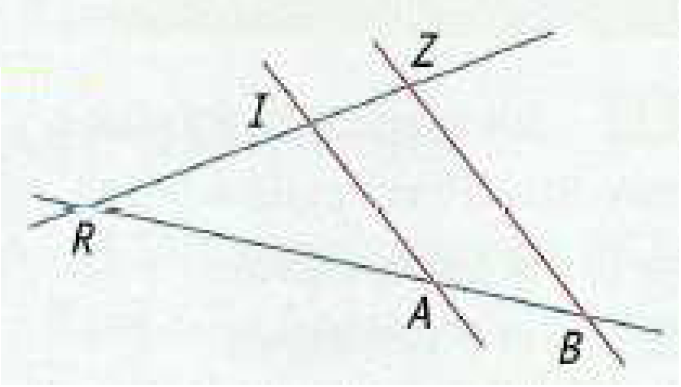
$\dfrac{RA}{RB} = \dfrac{RI}{RZ} = \dfrac{AI}{BZ}$ .
Problème numéro 3 :
On rappelle que l'équation d'une droite dans le plan est, la plupart du temps, $y=ax+b$ .
Soient $ A$ et $ B$ deux points du plan respectivement définis par $(1,5)$ et $(2,3)$ . Quelle est l'équation de la droite $ AB$ ?
Pourquoi avoir pris la précaution d'écrire la plupart du temps ?
Donner la formule générale pour l'équation de la droite du plan qui relie les deux points $A(x_A,y_A)$ et $B(x_B,y_B)$ .
Quelle erreur de notation a été commise dans cet énoncé ?
solution
Si $y=ax+b$ est l'équation vérifiée par les coordonnées $(x,y)$ des points $ A$ et $ B$ alors on a deux équations à résoudre ensemble :
(E1) : $5=a\times 1+b$
(E2) : $3=a\times 2+b$
Si on soustrait (E1) de (E2), il reste $-2=a$ . En reportant la valeur de $ a$ dans ces deux équations, on trouve $b=7$ .
L'équation cherchée est donc : $y=-2x+7$ .
Vérifions : pour $ A$ : $-2\times 1 +7=-2+7=5$ ; pour $ B$ : $-2\times 2 +7=-4+7=3$ . C'est bon !
On a écrit la plupart du temps parce que la vraie équation générale d'une droite est $\alpha x+\beta y =\gamma$ .
La formulation $y=ax+b$ ne couvre pas les cas où les droites sont de la forme $x=$ constante .
Dans le cas général où on veut déterminer les valeurs de $ a$ et de $ b$ pour une droite qui passe par les deux points $M_1$ et $M_2$ de coordonnées respectives $(x_1,y_1)$ et $(x_2,y_2)$ , il serait tentant de reprendre les deux équations
(E1) : $y_1=a\times x_1+b$ et (E2) : $y_2=a\times x_2+b$ .
Si on soustrait (E1) de (E2), il reste $y_2-y_1=a(x_2-x_1)$ d'où, péniblement, $a=\dfrac{y_2-y_1}{x_2-x_1}$
et il faudrait encore reporter cela dans les équations pour trouver la valeur de $ b$ .
Heureusement, il existe une méthode plus simple car tout segment d'une droite a la même pente.
Il suffit donc de considérer les pentes des segments $MM_1$ et $M_2M_1$ pour un point $ M$ de coordonnées $(x,y)$ sur la droite.
Cela s'écrit :$\dfrac{y-y_1}{x-x_1}=\dfrac{y_2-y_1}{x_2-x_1}$ .
Si on note $a$ la pente (bien sûr !) qui vaut $\dfrac{y_2-y_1}{x_2-x_1}$ alors l'équation est $y -y_1=a(x-x_1)$ soit encore $y = ax + (y_1-ax_1)$ .
Vérifions : Pour les points $ A$ et $ B$ on a respectivement $x_1=1$ , $y_1=5$ , $x_2=2$ et $y_2=5$ .
La pente $ a$ vaut donc $\dfrac{y_2-y_1}{x_2-x_1}=\dfrac{3-5}{2-1}=-2$ . L'équation est $y = ax + (y_1-ax_1)=-2x+(5-(-2)1)$ soit encore $y = -2x + 7$ . C'est bon !
L'erreur de notation est de parler de la droite $ AB$ alors que cette notation désigne le segment $ AB$ , car il manque les parenthèses. La droite qui passe par $ A$ et $ B$ se note $ (AB)$ .
Problème numéro 4 :
Après avoir pris connaissance de la figure ci-dessous, déterminer, en justifiant votre réponse, la longueur de GL.
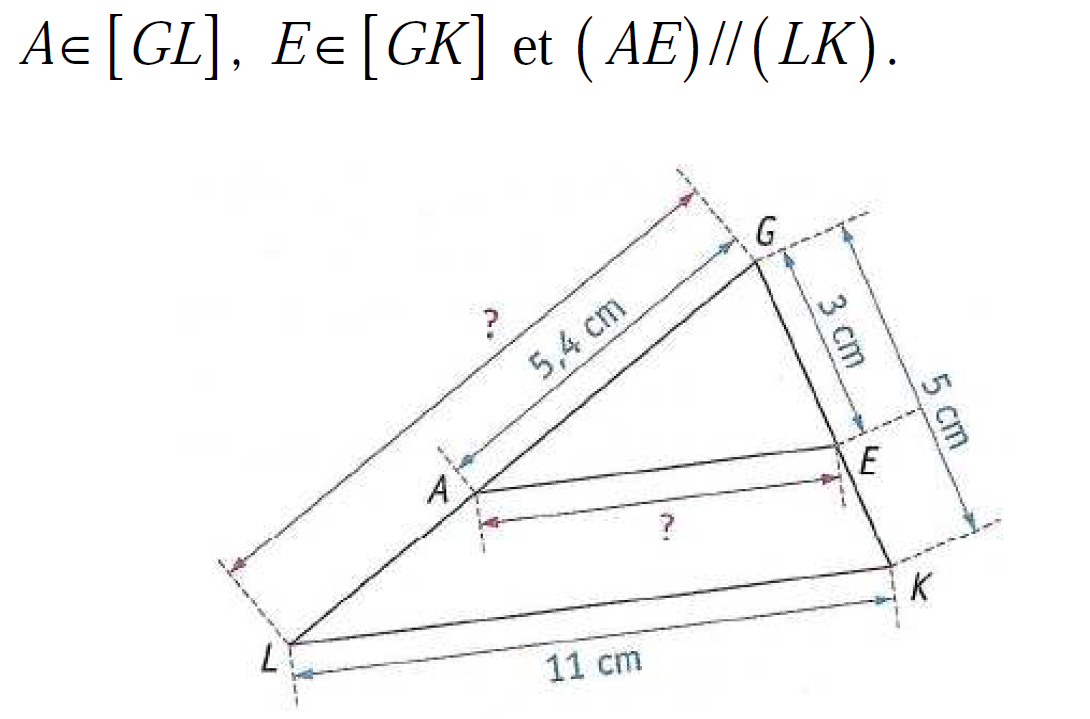
solution
Puisque AE et LK sont parallèles d'après la notation (AE)//(LK) , on peut appliquer le théorème de Thalès pour les segments issus de G :
$\dfrac{GA}{GL}=\dfrac{GE}{GK}$
On en déduit que $GL=\dfrac{GA\times GK}{GE}=\dfrac{5,4\times 5}{3}=\dfrac{27}{3}$
donc au final $GL=9\ cm$
Problème numéro 5 :
On considère les trois points du plan définis par $A=(1,5)$ , $B=(2,3)$ et $C=(1,3)$ .
Tracer les points dans le plan. Rappeler comment on calcule la distance entre deux points du plan.
Calculer les distances AB, BC et AC. ABC est-il un triangle rectangle ?
solution
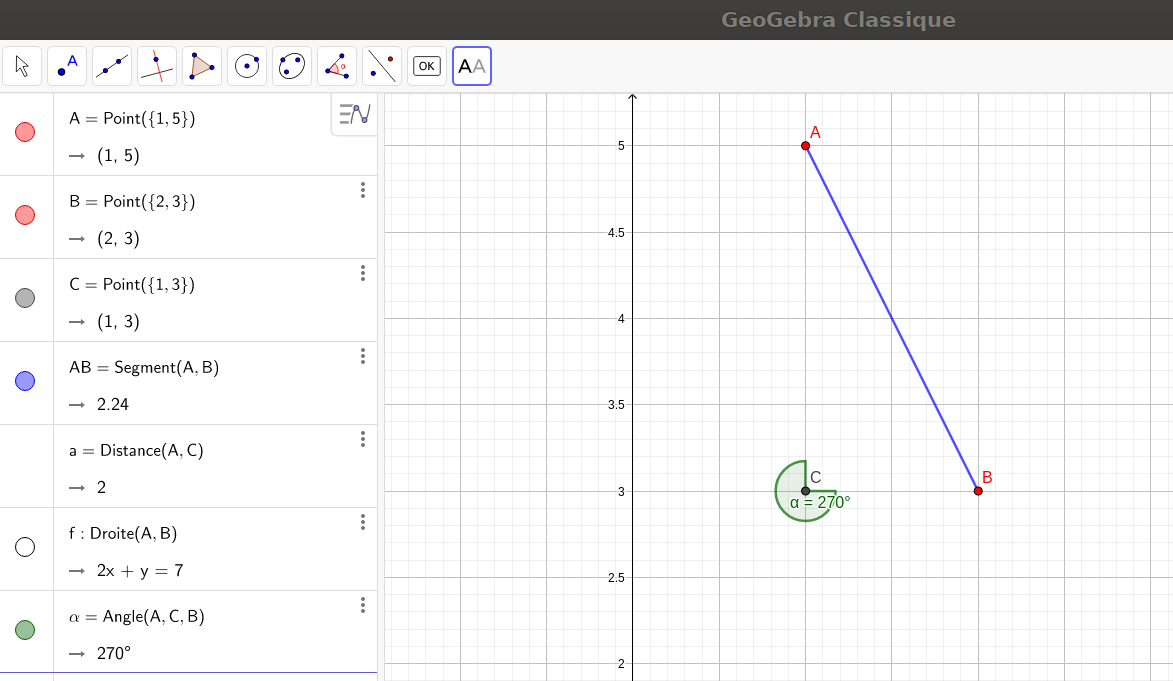
La longueur du segment qui relie $M_1=(x_1,y_1)$ et $M_2=(x_2,y_2)$ est donnée par la formule
$M_1M_2=\sqrt{ (x_1-x_2)^2 + (y_1-y_2)^2}$
Pour $ AB$ on trouve donc $\sqrt{ (1-2)^2 + (5-3)^2}=\sqrt{(-1)^2+2^2}=\sqrt{1+4}=\sqrt{5}\ \simeq 2.24$ .
De même, $AC=\sqrt{ (1-1)^2 + (5-3)^2}=\sqrt{0^2+2^2}=2$ .
Enfin, $BC=\sqrt{ (2-1)^2 + (3-3)^2}=\sqrt{1^2+0^2}=1$ .
La somme $AC^2+BC^2$ vaut $2^2+1^2=4+1=5$ . Comme $AB^2=5$ le triangle $ ABC$ est rectangle via la réciproque du théorème de Pythagore.
L'angle droit est en face de l'hypothénuse qui est $ AB$ , le plus grand coté. C'est donc l'angle $\widehat{ACB}$ .
4. Paradoxes géométriques
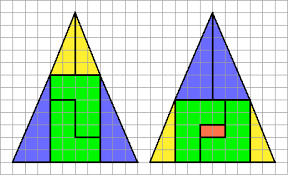
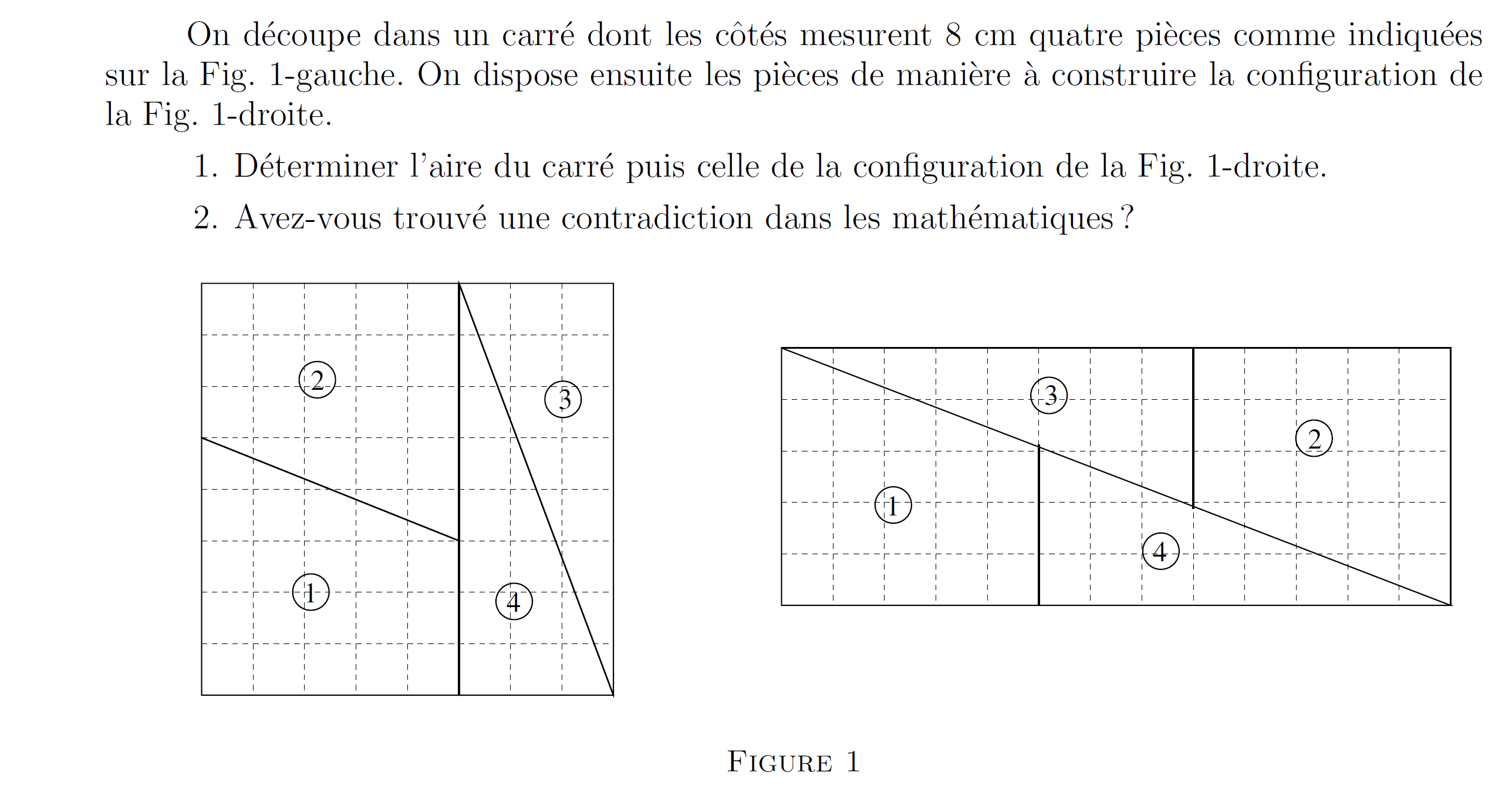
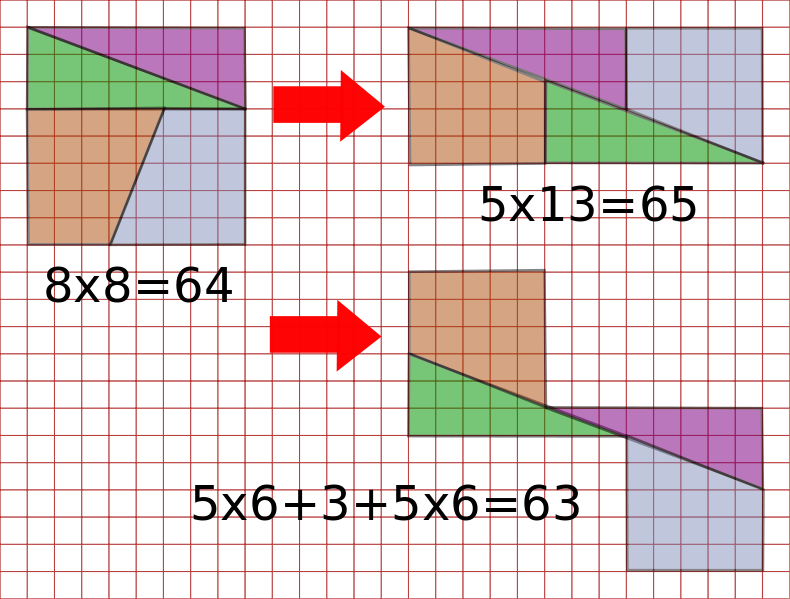
Les dessins suivants semblent montrer des contradictions mathématiques : si on découpe les morceaux et si on les réassemble, on obtient plus de surface ou moins de surface qu'auparavant.
Vous pouvez le vérifier par vous-mêmes si vous avez une imprimante et des ciseaux...
Où est le truc ?
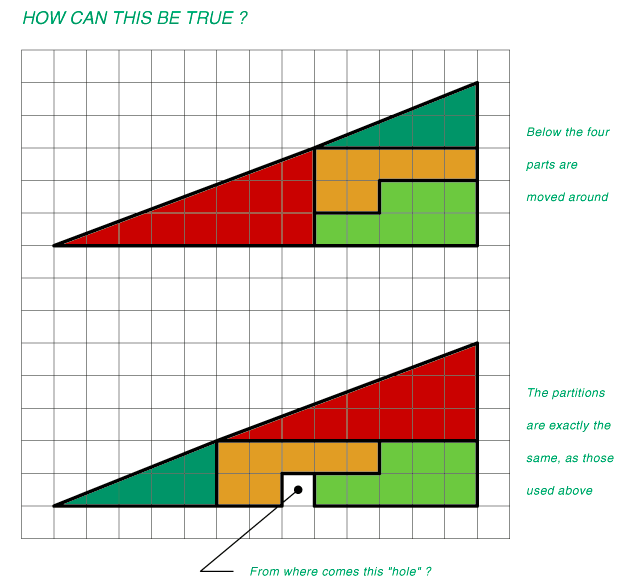
Et un dernier pour la route :

solution
Il n'y a pas d'erreur ni de contradiction, seulement des illusions visuelles.
Ainsi, pour la deuxième figure, les morceaux découpés ne sont pas complètement jointifs et la surface manquante, très mince, vaut 1.
Elle est difficile à voir et à imaginer. En voici une représentation :
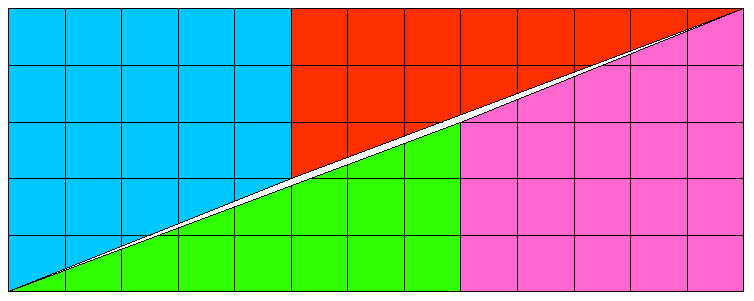
On retrouvera le dessin initial sur la page fibo1 et l'explication du paradoxe sur la page fibo2.
Pour l'image avec les nains, les meilleures explications sont sans doute dwarfR, 25280182 et la vidéo 5510566.
retour au plan de cours
|
 Retour à la page principale de
(gH)
Retour à la page principale de
(gH)