gilles.hunault@univ-angers.fr

   cabIq Automatique, Bactéries, Classification, Identification, Quarantaine

Accès rapide :

Exemple de classification

Exemple d'identification

 

Exemple commenté de classification

Cet exemple correspond au premier exemple proposé dans le panneau interactif de classification que vous pouvez activer en cliquant ici. Il y a 3 individus à classer nommés respectivement Adam, Eve et Lilith. Ces individus ont répondu à une série de 5 tests. Par exemple on peut imaginer qu'on leur a demandé s'ils prenaient ou non au petit déjeuner : du Café (1), du Thé (2), du Pain (3), du Beurre (4), du Gingembre (5). Adam qui prend du café (1) et du pain (3) a donc comme liste de positivité 1 3. De meme, Eve qui prend du thé, du pain et du beurre a pour liste 2 3 4 et enfin Lilith qui prend tout sauf du café a comme liste 2 3 4 5. D'où les listes de positivité : Adam 1 3 Eve 2 3 4 Lilith 2 3 4 5 qu'on peut judicieusement afficher comme Adam 1 3 Eve 2 3 4 Lilith 2 3 4 5 La matrice des données correspondante en codage disjonctif binaire complet est alors café thé pain beurre gingembre Adam 1 0 1 0 0 Eve 0 1 1 1 0 Lilith 0 1 1 1 1 C'est la matrice pour laquelle un 1 en ligne i colonne j signifie que l'individu i a répondu positivement au test numéro j. La matrice des distances au sens de Jaccard-Sneath se calcule alors de la façon suivante : pour deux lignes dans la matrice des données, on calcule le nombre ND de tests pour lesquels ces lignes n'ont pas le meme resultat (l'une a 1 et l'autre 0 ou l'inverse), le nombre NE de test pour lesquel l'un des deux lignes au moins a le resultat 1 puis on effectue le rapport ND/NE. Par exemple la distance entre Adam et Eve se calcule comme suit : ND = 3 (1 pour le café, le thé et le beurre), NE = 4 (tous les tests sauf le gingembre) d'où d = 3/4 soit 0.75. Chaque individu est bien sur à une distance 0 de lui-meme et l'ensemble des distances est résumée dans la matrice triangulaire inférieure suivante : Adam Eve Lilith Adam 0.0000 Eve 0.7500 0.0000 Lilith 0.8000 0.2500 0.0000 La première étape de la classification selon le critère de la distance minimale et du recalcul selon la formule dite UPGMA consiste à trouver les individus de distance minimale, à les regrouper et à recalculer la distance des autres individus à ce nouveau groupe. Ici la distance minimale est obtenue pour Eve et Lilith (valeur 0.25) et la distance entre Adam et le groupe Eve-Lilith se calcule par la moyenne des distances Adam-Eve et Adam-Lilith soit ici 0.75+0.80 donc 0.775. Puisqu'il n'y a plus que deux éléments à classer : Adam Eve-Lilith Adam 0.0000 Eve-Lilith 0.7750 0.0000 la nouvelle distance minimale est 0.775 et on regroupe Adam et Eve-Lilith. On résume ces regroupements binaire à l'aide des numéros de groupe : au départ chaque individu est un groupe à lui tout seul, soit personne groupe Adam 1 Eve 2 Lilith 3 Le premier groupe formé regroupait Eve (groupe 2) et Lilith (groupe 3). Puisqu'on le met à la suite des autres, c'est le groupe 4. Il est intéressant de noter la distance à laquelle on a regroupé et aussi le nombre de personnes dans un groupe. C'est pourquoi la classification est décrite par les renseignements Groupe Niveau Aine Benjamin Effectif 4 0.250 3 2 2 5 0.775 4 1 3 Le dindon ou dendrogramme correspondant est un graphique qui illustre les regroupements avec leurs niveaux, soit ici

Plus généralement la classification au sens du critère de la distance minimale avec comme formule de recalcul dite UPGMA (unweighted pairgroup method with averages) consiste à les individus de distance minimale, à les regrouper et à recalculer la distance des autres individus à ce nouveau groupe par une formule de moyenne pondérée. Comme il s'agit d'une classification binaire, si on regroupe les classes Ga et Gb d'effectif respectif Ea et Eb en la classe Gc d'effectif Ec = Ea + Eb alors la distance entre Gc les autres éléments Gx se calcule par d( Gc, Gx ) = ( Ea * d(Ga, Gx) + Eb * d(Gb, Gx) ) / ( Ea + Eb ) Par exemple, si on est rendu à classer les éléments suivants Groupe Effectif | Matrice | G01 G11 G15 G18 G01 1 | 0.000 G11 1 | 0.888 0.000 G15 5 | 0.576 0.876 0.000 G18 4 | 0.529 0.774 0.531 0.000 alors on doit regrouper les groupes G01 et G18 en le groupe G19 avec une distance minimale de 0.529 et la distance entre G15 et G19 est (1*0.576+4*0.531)/(1+4) soit 0.54, la distance entre G11 et G15 reste inchangée, à savoir 0.876 et la distance entre G15 et G19 est (1*0.888+4*0.774) soit 0.7968 et les nouveaux éléments à classer sont : Groupe Effectif | Matrice | G11 G15 G19 G11 1 | 0.000 G15 5 | 0.876 0.000 G19 5 | 0.797 0.540 0.000

 

Il y a équivalence entre la description de la classification et le dendrogramme associé. Par exemple, à partir du graphique

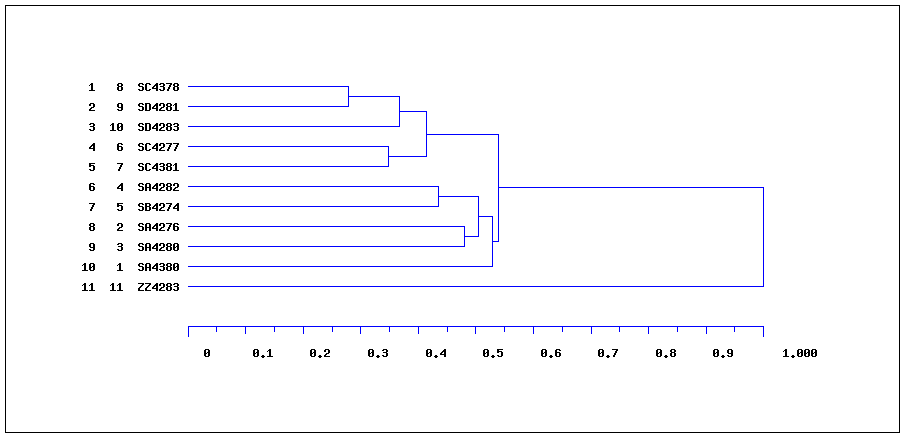
il est relativement simple de déduire les classes initiales Groupe Nom 1 SA4380 2 SA4276 3 SA4280 4 SA4282 5 SB4274 6 SC4277 7 SC4381 8 SC4378 9 SD4281 10 SD4283 11 ZZ4283 puis les regroupements (avec des distances sans doute plus approximatives, si on mesure sur le graphique) : Groupe Distance Aine Benjamin Effectif 12 0.278 9 8 2 13 0.348 7 6 2 14 0.367 12 10 3 15 0.414 14 13 5 16 0.435 5 4 2 17 0.480 3 2 2 18 0.505 17 16 4 19 0.529 18 1 5 20 0.540 19 15 10 21 1.000 20 11 11

 

Exemple commenté d'identification

 

Plutot que de reprendre en français l'exemple du CCUG nous allons détailler l'exemple 3 du panneau interactif d'identification que vous pouvez activer en cliquant ici. Cet exemple est celui de la page 371 et suivantes du chapitre 10 Computer-Assisted Identification de l'ouvrage Handbook of New Bacterial Systematics, édité par Goodfellow, M and 0. McDonnell (eds.) chez Academic Press en 1993. Cet exemple est lui-même une reprise d'un article de Wilcox paru en 1980 (voir notre bibliographie succinte). L'identification au niveau des calculs est beaucoup plus simple que la classification. Elle est par contre plus délicate au niveau de l'interprétation et beaucoup plus sensible au choix des données. Pour notre exemple nous disposons de 3 taxons (ou classes) prédéfinis nommés A, B et C dans l'ouvrage ou numérotés de façon équivalente 1, 2 et 3 si besoin est. Ces taxons correspondent aux lignes de la matrice d'entrée et ne sont connus pour le programme d'identification que par les lignes de la matrice d'entrée. Chaque ligne correspond aux fréquences de positivité des taxons pour les tests réalisés. Il y a ici 3 colonnes dans la matrice cela signifie donc que l'on travaille sur 3 tests. On peut imaginer, pour prendre un exemple biologique, que les taxons correspondent à des espèces, par exemple taxon A ou 1 = Salmonella ferlac taxon B ou 2 = Salmonella pullorum taxon C ou 3 = Salmonella typhi et que les tests sont des caractères biologiques comme test 1 : production d'Arginine dihydrolase test 2 : production de Lysine decarboxylase test 3 : mobilité forte à 37 degrés Celsius Les taxons s'interprétent alors comme des groupes de souches correspondant à l'espèce et les fréquences de positivité sont les pourcentages de positivité pour l'ensemble des souches de l'espèce pour les caractères retenus. Pour prendre un exemple plus explicite, on peut imaginer que les taxons sont des orchestres, comme taxon A ou 1 = orchestre anglais taxon B ou 2 = orchestre américain taxon C ou 3 = orchestre hongrois et que les tests sont les réponses aux questions test 1 : prenez-vous du café au petit-déjeuner ? test 2 : prenez-vous du thé au petit-déjeuner ? test 3 : prenez-vous du beurre au petit-déjeuner ? Les fréquences de positivité peuvent alors s'interpréter comme le pourcentage de musiciens d'un orchestre donné prenant l'ingrédient considéré. L'identification d'une bactérie ou d'un individu connu par sa seule liste de positivité consiste à trouver le taxon auquel l'individu appartient et à valider cette appartenance.

 

Pour notre exemple, la matrice est | test 1 | test 2 | test 3 --------+------------+----------+---------- taxon 1 | 0.99 | 0.99 | 0.01 taxon 2 | 0.95 | 0.50 | 0.99 taxon 3 | 0.80 | 0.01 | 0.01 et la liste de positivité de l'individu à identifier est 1 3 ce qu'on doit interpréter comme la suite de résultats | test 1 | test 2 | test 3 --------+------------+----------+---------- inconnu | 1.00 | 0.00 | 1.00 aux tests.

 

Pour mener à bien l'identification, on commence par calculer la liaison entre l'individu inconnu et chaque taxon. Cette liaison est quantifiée par une valeur numérique nommée "produit d'association global" ou "coefficient de vraisemblance" (likelihood) calculé comme le produit des liaisons entre l'individu inconnu et chaque test, la liaison étant calculée par la formule : liaison entre individu inconnu et test pour le taxon = la fréquence du test pour le taxon si la valeur de l'indidvidu au test est 1 = 1-fréquence du test pour le taxon si la valeur de l'indidvidu au test est 0 Ainsi la liaison entre notre inconnu et le taxon 1 vaut 0.99 pour le test 1 1-0.99 pour le test 2 soit 0.01 0.01 pour le test 3 d'où un produit d'association global entre l'inconnu et le taxon 1 pour l'ensemble des trois tests égal à 0.99 * 0.01 * 0.01 soit 0.000099, ce que le logiciel affichera comme * 0.0000 pour éviter d'afficher trop de décimales. Reprenant les mêmes calculs pour les taxons 2 et 3 on arrive finalement au tableau Taxon | Produits d'association globaux --------+------------------------------------------- T1 | * 0.0000 valeur exacte 0.000099 T2 | 0.4702 0.470250 T3 | 0.0079 0.007900 --------------- total 0.478249 Les produits d'associations globaux sont ensuite pondérés de deux façons : le produit d'association relatif est obtenu en divisant le produit d'association global par le plus grand produit d'association global (soit ici 0.4702) et le produit d'association normalisé est obtenu en divisant le produit d'association global par la somme des produits d'associations globaux (soit ici 0.478249). Le produit d'association normalisé est nommé également score d'identification de ou probabilité de Wilcox ou pourcentage d'identification d'où pour notre exemple les résultats Taxon | Produits d'associations globaux --------+------------------------------------------- | valeurs normalisés relatifs | (SCORE) T1 | * 0.0000 0.02 % 0.02 % T2 | 0.4702 98.32 % 100.00 % T3 | 0.0079 1.66 % 1.68 % ce qui s'interpréte ici comme : l'inconnu semble appartenir au taxon 2.

 

Il reste maintenant à valider le choix du taxon. Pour cela, on commence par calculer les coefficients modaux globaux (ou coefficients globaux de modalité) pour les taxons. Comme pour les produits d'associations globaux, le coefficient modal global pour un taxon est le produit des coefficients modaux locaux de chaque test pour le taxon, calculé comme suit : le coefficient modal local du test pour le taxon = la fréquence du test pour le taxon si cette féquence est supérieure à 0.5 = 1 - fréquence du test pour le taxon si cette féquence est inférieure à 0.5 Ainsi le coefficient modal local du taxon 1 vaut 0.99 pour le test 1 0.99 pour le test 2 1-0.01 pour le test 3 soit 0.99 soit un coefficient modal global de 0.0970299 pour le taxon 1. Ce coefficient modal est également appelé coefficient de vraisemblance maximum pour le taxon. Avec les arrondis, notre programme affiche donc, en effectuant les mêmes calculs pour les deux autres taxons Taxon | Coefficients modaux globaux -------+------------------------------- T1 | 0.9703 T2 | 0.4702 T3 | 0.7841

 

La validation de l'identification est donnée par les probabilités modales de l'appartenance de l'individu au taxon, nommées aussi fractions modales de vraisemblance, calculées comme le rapport "produit d'association global sur coefficient modal global". Par exemple pour l'individu et le taxon 1, le produit d'association global est 0.000099 le coefficient modal global est 0.970299 donc la probabilité modale est 0.000096059601 exprimée comme 0.01 %. Finalement, tous calculs faits, on obtient le tableau récapitulatif Taxon | Produits d'associations | valeur fréquence relatif | SCORE Id. --------+----------------------------------------- T1 | * 0.0000 0.02 % 0.02 % T2 | 0.4702 98.32 % 100.00 % T3 | 0.0079 1.66 % 1.68 % Taxon | Coefficients modaux | valeur probabilité | VALIDn --------+---------------------------------------- T1 | 0.9703 0.01 % T2 | 0.4702 100.00 % T3 | 0.7841 1.01 qui permet de dire que l'individu appartient au taxon 2.

 

Le cas théorique "parfait" ou chaque colonne correspond à une classe comme par exemple pour la matrice | test 1 | test 2 | test 3 | test 4 --------+------------+----------+----------+---------- taxon 1 | 1.00 | 0.00 | 0.00 | 0.00 taxon 2 | 0.00 | 0.10 | 0.00 | 0.00 taxon 3 | 0.00 | 0.00 | 1.00 | 1.00 n'est pas facile à gérer : en effet, l'inconnu avec la liste de positivité 1 tout va bien (on valide son appartenance au taxon 1) mais pour l'inconnu avec la liste de positivité 3 4 on obtient des divisions par zéro ! C'est pourquoi en général dans les matrices de fréquence on note 0.99 la valeur maximum et 0.01 la valeur minimum. Si donc on prend la matrice | test 1 | test 2 | test 3 | test 4 --------+------------+----------+----------+---------- taxon 1 | 1.00 | 0.00 | 0.00 | 0.00 taxon 2 | 0.00 | 1.00 | 0.00 | 0.00 taxon 3 | 0.00 | 0.00 | 1.00 | 1.00 alors la liste de positivité 1 est identifiée comme appartenant au taxon 1 alors que la liste 3 n'est pas identifié comme appartenant au taxon 3 : il faut impérativement utiliser la liste de positivité 3 4 pour être identifié comme appartenant bien au taxon 3. On comprend donc que le choix des tests influe énormément sur l'identification : et la pertinence du choix des colonnes n'est pas une mince affaire. Il faut en général recourir à des programmes de choix des colonnes dsicrimiinantes à partir de souches de référence données dans les taxons. Mais ceci est une autre histoire... et se nomme CCD.

 

Utiliser 0.99 ou 0.999 comme valeur maximale fournit en principe les mêmes conclusions mais pas les mêmes valeurs numériques. On pourra s'en rendre compte en comparant les résultats de l' exemple 5 et de l' exemple 6.

  Retour à la page principale de cabIq