Décomposition, Conception et Réalisation d'Applications T.D. 2 : Structuration, instructions vectorielles, boucles et optimisation                     gilles.hunault "at" univ-angers.fr Table des matières cliquable   1. Structuration dans le développement Web   2. Instructions vectorielles et fonctionnelles (1)   3. Instructions vectorielles et fonctionnelles (2)   4. Boucles et optimisation (1)   5. Boucles et optimisation (2)   6. Optimisation dans le développement Web Il est possible d'afficher toutes les solutions via ?solutions=1 et de les masquer via ?solutions=0.   1. Structuration dans le développement Web Comment fait-on pour structurer une page Web ou un site Web en PHP ? Comment fait-on pour structurer un programme en général ? Faut-il passer à des sites Web non écrits en PHP ? Que signifie le terme full stack ? Solution :     masquer la solution   Il n'y a pas de solution générale à la structuration, que ce soit une page Web, un site Web ou un programme en général, même si la plupart des langages de programmation fournissent des moyens d'inclure des fichiers. Rien n'indique en effet comment découper le code ou quelles fonctions mettre dans quels fichiers. Structurer une page Web consiste en général à externaliser le code CSS et le code Javascript, et sans à doute définir des sous-programmes d'affichage. En fonction de l'importance de la page, on viendra donc inclure ou plusieurs fichiers PHP, on utilisera des bibliothèques Javascript pour le front end et le back end. Comment structurer un site page Web est un problème compliqué. La tendance actuelle (2018) consiste plutôt, pour un blog ou un site de moyenne importance, à passer par un générateur de sites nommé dans ce contexte CMS comme par exemple WordPress. Pour des sites plus complets, ou si on préfère plus de controle sur le site, il est conseillé de passer par un framework de développement comme Laravel, CakePHP, Symfony, CodeIgniter ou Joomla. La plupart des sites ainsi générés sont alors structurés selon une architecture proche de MVC plutôt que d'une architecture trois tiers. La question de savoir s'il faut développer en PHP, en Java ou autre langage n'est pas un problème simple. La popularité de Django, Ruby on Rails et NodeJs montre que PHP et Java ne sont pas les seuls langages possibles pour développer des sites Web. Les langages utilisés, respectivement Python, Ruby et Javascript, ont suffisamment d'avantages pour qu'on se pose la question de leur utilisation. Le terme fullstack fait référence à des compétences de développement Web qui couvrent tous les aspects du développement. On pourra consulter la page Web de wikipedia sur le sujet.         2. Instructions vectorielles et fonctionnelles (1) La programmation vectorielle met en jeu des instructions basées, soit en entrée, soit en sortie, sur des structures de type tableau mais nommées vecteurs par analogie avec les vecteurs mathématiques de $\mathbf{\Bbb{R}^n}$. On notera pour cet exercice $V_i$ la i-ème composante du vecteur $V$, équivalente à V[i] ou V[i-1] pour l'informatique. Les calculs usuels s'étendent naturellement aux vecteurs, comme en mathématiques, dès lors que les contraintes de longueur sont respectées. En particulier, pour un vecteur $V$ et un nombre $a$, le vecteur $aV$ a pour i-ème composante la valeur $aV_i$. Pour deux vecteurs $V$ et $W$ de même longueur, $V+W$ est le vecteur dont la i-ème composante est $V_i+W_i$, et $V\times{}W$ est le vecteur dont la i-ème composante est $V_i\times{}W_i$ («produit scalaire»). On admettra pour ce qui suit qu'on dispose des fonctions vectorielles suivantes : indices(n) qui renvoie, pour un entier $n$, le vecteur de longueur $n$ dont la i-ème composante est $i$  longueur(V) qui renvoie le nombre d'éléments du vecteur V ; somme(V) qui renvoie la somme des éléments du vecteur V ; produit(V) qui renvoie le produit des éléments du vecteur V ; cumul(V) qui renvoie le vecteur des sommes cumulées de V ; Donner les instructions vectorielles qui permettent de calculer : - le vecteur $I$ des $n$ premiers entiers ; - la somme $S = \sum i$ des $n$ premiers entiers ; - la somme $C = \sum i^2$ des n premiers carrés d'entiers ; - la valeur $F = n!$ ("factorielle n") ; - la moyenne $M$ et la variance (empirique) $V$ d'un vecteur $W$ numérique ; - le vecteur $P$ des fréquences cumulées d'un vecteur $W$ d'effectifs (positifs ou nuls) de somme non nulle. On pourra imaginer que $n$ vaut 5 pour vérifier les calculs à la main, et que $W$ est le vecteur (1,5,3,1). Quels langages implémentent de tels calculs ? Quelle est alors la syntaxe exacte à utiliser ? Solution :     masquer la solution   Les langages R et APL implémentent ces calculs de façon native. Python les implémente via le package NumPy. Sans rien installer, pour APL, on peut utiliser le site tryapl.org à cause des caractères spéciaux. Pour R et Python, là encore sans rien installer, on peut utiliser en ligne, le site https://repl.it ou les jupyter notebook à l'adresse try jupyter. Pour Python, on a "importé" les fonctions array, arange et shape de numpy. Certaines solutions avec la syntaxe objet ont un équivalent traditionnel, comme par exemple sum(I) au lieu de I.sum(). Algorithmique Langage R Langage APL Langage Python Résultat I <-- indices(n) I <- 1:n I ← ιn I = arange(1,n+1) (1,2,3,4,5) S <-- somme(I) S <- sum(I) S ← +/I S = I.sum() 15 C <-- somme(I×I) C <- sum(I*I) C ← +/I×I C = (I*I).sum() 55 F <-- produit(I) F <- prod(I) F ← ×/I F = I.prod() 120 M <-- somme(W) / longueur(W) M <- sum(W) / length(W) M ← (+/W) ÷ ρW M = W.sum()/shape(W) 2.5 V <-- somme( (W-M)^2 ) / longueur(W) V <- sum((W-M)**2) / length(W) V ← (+/(W-M)*2)) ÷ ρW sum((W-M)**2)/shape(W) 2.75 P <-- cumul(W) / somme(W) P <- cumsum(W) / sum(W) P ← (+\W) ÷ +/W P = W.cumsum()/W.sum() (0.1,0.6,0.9,1.0) Remarques : APL a une fonction spécialisée pour calculer factorielle n. Et l'opération de réduction via / peut s'appliquer à n'importe quel opérateur. R a des fonctions spécialisées pour calculer factorielle n, la moyenne et la variance, sachant qu'en statistiques, il y a plusieurs variances (dont celle de l'échantillon, celle de la population sous-jacente). Python, via NumPy notamment, dispose aussi de fonctions spécialisées pour réaliser de tels calculs. Attention à l'écriture "propre" des appels de fonctions dans ces langages. Ainsi en R, sum(I)*I et sum(I*I) sont tous deux des calculs valides mais qui ne fournissent pas le même résultat. En Python aussi, avec I*I.sum() et (I*I).sum(). Il est donc important de vérifier que le code produit bien ce qu'on veut.   3. Instructions vectorielles et fonctionnelles (2) On suppose désormais que les comparaisons logiques usuelles sont aussi des opérations vectorielles qui renvoient, indice par indice, 0 lorsque le résultat du test est faux et 1 lorsque le résultat du test est vrai. Ainsi, pour le vecteur $V=(5,8,2,1,9)$, la comparaison $V>3$ renvoie $(1,1,0,0,1)$. Détailler ce que réalisent les calculs suivants écrits en APL, sachant que Γ correspond à la fonction max(). On pourra essayer d'inventer la syntaxe algorithmique correspondante et on se posera la question de savoir comment écrire cela en R puis en Python, sans doute là encore à l'aide de NumPy. Atttention : APL interprète les opérations à partir de la droite afin de minimiser le nombre de parenthèses à écrire. Ainsi 2 × 3 +5 correspond à 2 × (3 +5) soit 16. Numéro Instruction APL Remarque 1     V=W V et W sont des vecteurs numériques ou caractères 2     +/V=W V et W sont des vecteurs numériques ou caractères 3     +/V>0 V est un vecteur numérique 4     +/Γ/V=V V est un vecteur numérique 5     +/V=Γ/V V est un vecteur numérique 6     +/V$\times$W V est un vecteur numérique 7     +/V$\times$V V est un vecteur numérique On commencera par donner le vecteur résultat correspondand à chaque instruction pour les vecteurs $V=(5,8,-2,1,8)$ et $W=(5,8,2,1,9)$. Solution :     masquer la solution   Voici les résultats pour les vecteurs $V$ et $W$ fournis : Numéro Instruction APL Résultat Remarque(s) 1   V=W ($1,1,0,1,0)$ Les différences sont aux indices 3 et 5. 2   +/V=W 3 C'est la somme du vecteur précédent. 3   +/V>0 4 Il y a 4 valeurs strictement positives dans $V$. 4   +/Γ/V=V 1 $V=V$ renvoie $(1,1,1,1,1)$. ($Γ/V=V$) est donc 1 et $+/1$ renvoie 1. 5   +/V=Γ/V 2 Γ/V est 8. $V=Γ/V$ est $(0,1,0,0,1)$. Sa somme est 2. 6     +/V$\times$W 158 V$\times$W est (25,64,-4,1,72). Sa somme est 158. 7     +/V$\times$V 158 (aussi !) V$\times$V est (25,64,4,1,64). Sa somme est 158. La première instruction renvoie le vecteur des comparaisons terme à terme des vecteurs V et W. La deuxième instruction renvoie le nombre egal(V,W) de valeurs égales dans V et W à la même position. Un calcul lié à cette instruction est le nombre diff(V,W) de valeurs différentes entre V et W. La fonction (V,W) $\mapsto$ diff(V,W) est nommée distance de Hamming. Cette distance est très utilisée en bioinformatique et en informatique textuelle. La troisième instruction renvoie le nombre de valeurs strictement positives dans le vecteur V. La quatrième instruction correspond sans doute à une erreur de frappe. Elle renvoie 1 systématiquement. La cinquième instruction renvoie le nombre de valeurs dans le vecteur V égales au maximum de V. C'est sans doute la bonne version de l'instruction 4. La sixième instruction renvoie la somme des produits terme à terme des vecteurs V et W. C'est donc ce qu'en algèbre (linéaire) on nomme le produit scalaire de ces vecteurs. La septième instruction renvoie le produit scalaire d'un vecteur avec lui-même. C'est donc ce qu'en algèbre on nomme le carré de la norme de ce vecteur. Code R correspondant : V <- c(5,8,-2,1,8) W <- c(5,8, 2,1,9) cat("1. V==W : ",as.numeric(V==W),"\n") # sans as.numeric : TRUE TRUE FALSE TRUE FALSE cat("2. +/V=W : ",sum(V==W),"\n") # as.numeric est utilisé automatiquement cat("3. +/V>0 : ",sum(V>0),"\n") cat("5. +/V==max(V) : ",sum(V==max(V)),"\n") # maxV <- max(V) ; sum(V==maxV) est sans doute mieux cat("6. +/V*W : ",sum(V*W),"\n") cat("7. +/V*V : ",sum(V*V),"\n") Résultats : 1. V==W : 1 1 0 1 0 2. +/V=W : 3 3. +/V>0 : 4 4. +/max(V==V) : 1 5. +/V==max(V) : 2 6. +/V*W : 158 7. +/V*V : 158 Code Python correspondant : import numpy as np V = np.array([5,8,-2,1,8]) W = np.array([5,8, 2,1,9]) print("1. V=W : ",V==W ) print("2. +/V=W : ",sum(V==W) ) # ou (V==W).sum() print("3. +/V>0 : ",sum(V>0) ) # ou (V>0).sum() print("4. +/max(V=V) : ",(V==V).max().sum() ) print("5. +/V=max(V) : ",sum(V==V.max()) ) # ou (V==V.max()).sum() print("6. +/VxW : ",sum(V*W) ) print("7. +/VxV : ",sum(V*V) ) Résultats : 1. V=W : [ True True False True False] 2. +/V=W : 3 3. +/V>0 : 4 4. +/max(V=V) : 1 5. +/V=max(V) : 2 6. +/VxW : 158 7. +/VxV : 158   4. Boucles et optimisation (1) On se donne deux valeurs numériques $a$ et $b$ et un entier $n$. Ecrire un algorithme qui calcule les valeurs des $n$ points équidistants $x_i$, $i$ de 1 à $n$ avec $a=x_1$ et $b=x_n$. On commencera par trouver la formule qui sépare deux points sucessifs. On discutera s'il faut utiliser une boucle pour, une boucle tant que, ou se passer de boucle et on viendra optimiser le nombre d'opérations. Au passage, que sont les $x_i$ pour $n=10$ avec $a=1$ et $b=10$ ? Et pour $n=11$ avec $a=0$ et $b=1$ ? Trouver ensuite une solution vectorielle. Quelles solutions sont proposées par R et Python ? Solution :     masquer la solution   La formule mathématique pour calculer les $x_i$ est bien sûr :        $x_i = a + (i-1)\times \displaystyle\frac{(b-a)}{(n-1)}$ Pour $n=10$, avec $a=1$ et $b=10$, les $x_i$ sont les nombres de 1 à 10. Pour $n=11$, avec $a=0$ et $b=1$, les valeurs sont 0 0.1 0.2... 1.0. La programmation naïve de la formule ne pose aucun problème : # calcul de chacun des points xi selon la formule # xi = a + (b-a)*(i-1)/(n-1) pour i de 1 à n # boucle naive lesXi1 <-- fonction(a,b,n) { xi <- vecteurVide() pour i de1a n xc <-- a + (i-1)*(b-a)/(n-1) xi <-- ajouteAuVecteur(xi,xc) fin_pour # i renvoyer( xi ) fin_fonction # lesXi1 Une première optimisation de la boucle consiste à sortir les «constantes» de la boucle et à initialiser le vecteur de sortie, soit le code : # calcul de chacun des points xi selon la formule # xi = a + (b-a)*(i-1)/(n-1) pour i de 1 à n # boucle un peu optimisée lesXi2 <-- fonction(a,b,n) xi <-- vecteurVide(n) h <-- (b-a)/(n-1) pour i de1a n xc <-- a + h*(i-1) xi[ i ] <-- xc fin_pour # i renvoyer( xi ) fin_fonction # lesXi2 Une deuxième optimisation consiste à remarquer que les $x_i$ sont en progression arithmétique, donc il suffit de rajouter le pas $h$ de la progression pour passer d'un point à l'autre : # calcul de chacun des points xi selon la formule # xi = a + (b-a)*(i-1)/(n-1) pour i de 1 à n # boucle très optimisée lesXi3 <-- fonction(a,b,n) { xi <-- vecteurVide(n) h <-- (b-a)/(n-1) xc <-- a - h pour i de1a n xc <-- xc + h xi[ i ] <-- xc fin_pour # i renvoyer( xi ) fin_fonction # lesXi3 Bien sûr le calcul vectoriel permet de se passer de boucle : # calcul de chacun des points xi selon la formule # xi = a + (b-a)*(i-1)/(n-1) pour i de 1 à n # calcul vectoriel (sans boucle) lesXi4 <-- fonction(a,b,n) { h <-- (b-a)/(n-1) xi <-- a + h*(sequence(1,n)-1) renvoyer( xi ) fin_fonction # lesXi4 Voici à titre d'exemple les versions 1 et 4 en R : # calcul de chacun des points xi selon la formule # xi = a + (b-a)*(i-1)/(n-1) pour i de 1 à n # boucle naive lesXi1 <- function(a,b,n) { xi <- c() for (i in (1:n) ) { xc <- a + (b-a)*(i-1)/(n-1) xi <- c(xi,xc) } # fin pour i return( xi ) } # fin de fonction lesXi1 ##################################################################### # calcul de chacun des points xi selon la formule # xi = a + (b-a)*(i-1)/(n-1) pour i de 1 à n # calcul vectoriel (sans boucle) # remarque : on aurait pu utiliser directement # seq(from=a,to=b,length.out=n) lesXi4 <- function(a,b,n) { h <- (b-a)/(n-1) xi <- a + h*((1:n)-1) return( xi ) } # fin de fonction lesXi4 Et leur équivalent en Python : # -*- coding:latin1 -*- import numpy as np # calcul de chacun des points xi selon la formule # xi = a + (b-a)*(i-1)/(n-1) pour i de 1 à n # boucle naive def lesXi1(a,b,n) : xi = [ a + (b-a)*(i-1)/(n-1) for i in range(1,n+1) ] return( xi ) # fin de fonction lesXi1 ##################################################################### # calcul de chacun des points xi selon la formule # xi = a + (b-a)*(i-1)/(n-1) pour i de 1 à n # calcul vectoriel (sans boucle) # on pourrait aussi utiliser np.linspace(start=a,stop=b,num=n) def lesXi4(a,b,n) : h = (b-a)/(n-1) xi = np.repeat(a,n) + h*np.asarray(range(n)) return( xi ) # fin de fonction lesXi4 La "vraie" solution se nomme seq() en R et linspace() en Python / NumPy avec les syntaxes suivantes : # solution R : seq(from=a,to=b,length.out=n) # solution Python : np.linspace(start=a,stop=b,num=n)   5. Boucles et optimisation (2) Comment calculer de façon optimisée le maximum, le nombre d'occurrences de ce maximum et sa première position pour un vecteur $V$ ? Est-ce qu'une solution vectorielle pour ce problème est forcément optimisée ? Quelles solutions sont proposées par R, APL et Python ? Le code proposé est-il valide pour des vecteurs de chaines de caractères plutôt que pour des vecteurs de nombres ? Solution :     masquer la solution   Un algorithme qui passe en revue chaque élément et décide si c'est le nouveau maximum (donc une seule occurrence) ou le maximum local (c'est-à-dire le maximum trouvé jusque-là, donc une occurrence de plus) est certainement un algorithme optimisé qui peut s'écrire en une seule boucle POUR, comme ci-dessous : # calcul du maximum du vecteur V # et de son nombre d'occurrences # et de la première position du maximum # (le tout en une seule boucle) affecter maximum <- V[ 1 ] # initialisation du maximum, affecter nbOcc <- 1 # du nombre d'occurrences affecter posMax <- 1 # et de la position du maximum pour indCour de 2 à longueur(V) eltCour <- V[ indCour] # élément courant en position indCour si (eltCour>maximum) # c'est le nouveau maximum maximum <- eltCour # donc on modifie maximum nbOcc <- 1 # c'est la première fois où on le voit posMax <- indCour # et il est en position courante sinon si (eltCour==maximum) # c'est une autre position du maximum nbOcc <- nbOcc + 1 # donc on incrémente nbOcc fin_si # égalité fin_si # supériorité stricte fin_pour # indCour Une solution vectorielle pour compter le nombre d'occurrences du maximum par exemple avec le code somme( V=max(V) ) est certes courte à écrire mais effectue deux parcours du vecteur. Cela s'écrit +/V=Γ/V en APL, sum( V==max(V) ) en R et (V==max(V)).sum() en Python. Une telle écriture est sans doute suffisante car le code sous-jacent est très rapide, même pour des millions d'éléments. Il faudrait vraiment avoir des milliers de chaines d'ADN humain complètes (3 milliards de caractères) à comparer pour que ce code vectoriel soit moins efficace que notre algorithme. Nous ne donnons pas ici, volontairement, les solutions vectorielles en R, APL et Python pour trouver la première position du maximum. Symboliquement, ce pourrait être premier( V=max(V) ) mais il faudrait alors "sortir" le vecteur V=max(V) de ce calcul pour éviter de le recalculer deux fois afin de résoudre le problème complet posé. Les solutions algorithmiques correspondantes sont indiquées ci-dessous. Version vectorielle non optimisée # calcul non optimisé du maximum du vecteur V # et de son nombre d'occurences # et de la première position du maximum # (algorithmique vectorielle) affecter nbOcc <- somme( V=max(V) ) affecter posMax <- premier( V=max(V) ) Version vectorielle optimisée # calcul du maximum du vecteur V # et de son nombre d'occurences # et de la première position du maximum # (algorithmique vectorielle optimisée) affecter testMax <- V=max(V) affecter nbOcc <- somme( testMax ) affecter posMax <- premier( testMax )   6. Optimisation dans le développement Web Ce qu'on a vu précédemment montre que dans de nombreux cas, des calculs simples comme le maximum, les valeurs d'une suite arithmétique sont déjà programmés. Peut-on penser que dans l'utilisation de bases de données, on trouve le même genre de solutions pré-programmées ? Et dans le cas du développement Web ? Comment garantir par exemple qu'une requête MySQL est optimisée ? Comment tester la vitesse d'exécution de code en R et en Python ? Solution :     masquer la solution   Oui, bien sûr, des solutions pré-programmées existent déjà pour les bases de donnnées. Par exemple en SQL, pour calculer le maximum ou la moyenne, il existe des fonctions nommées fonctions d'agrégation. comme min, max, avg et les variances. Savoir si une requête est optimisée, par contre, est loin d'être évident. Par exemple, comment savoir si la requête ci-dessous est optimisée ? USE DBDB ; SELECT CONCAT(pr_pdb_id , ch_name) AS nomProt , LENGTH(ch_fasta) AS longueur , pr_nbr_intra+pr_nbr_inter AS nbp , pr_nbr_intra AS nbintra , pr_nbr_inter AS nbinter , IF (pr_nbr_intra+pr_nbr_inter>0,"AVEC","SANS") AS pont , CASE WHEN pr_nbr_intra=0 AND pr_nbr_inter=0 THEN "ACUCUN" WHEN pr_nbr_intra=0 AND pr_nbr_inter>0 THEN "INTER_SEUL" WHEN pr_nbr_intra>0 AND pr_nbr_inter=0 THEN "INTRA_SEUL" WHEN pr_nbr_intra>0 AND pr_nbr_inter>0 THEN "INTER_ET_INTRA" END AS naturePont FROM dbdbprot a , dbdbchain b WHERE a.pr_id = b.ch_pr_id ; Ou comment décider si la requête 1 ci-dessous ## req1.sql # on doit trouver 6482 sur 20639 séquences use HSP ; select count(*) from fastas where length(substr(fasta,1,2000)) > (select avg(length(fasta)) from fastas) ; s'exécute plus rapidement que la requête 2 suivante # # (gH) -_- req2.sql # on doit trouver 6482 sur 20639 séquences use HSP ; set @moyLong = (select avg(length(fasta)) from fastas) ; select count(*) from fastas where length(substr(fasta,1,2000)) > @moyLong ; Même si MySQL, par exemple, dispose d'un mécanisme de profilage dont le modèle est reproduit dans le texte qui suit set profiling = 1 ; # +--------------------------------------------------------+ # | | # | mettre ici la ou les requêtes SQL à tester | # | | # +--------------------------------------------------------+ set profiling = 0 ; show profile ; # plus de détails à l'adresse : # # https://dev.mysql.com/doc/refman/8.0/en/show-profile.html il n'en demeure pas moins qu'exécuter une seule fois la requête et son profilage n'est certainement pas suffisant, sauf dans de très rares cas (à cause de l'encombrement mémoire, de la mise en cache des données, etc.). Donc on peut essayer d'estimer si une requête est optimisée, mais sans pouvoir vraiment le prouver. $gh> sql < req1.sql | $gh> sql < req2.sql | count(*) | count(*) 6482 | 6482 | Status Duration | Status Duration starting 0.000043 | starting 0.000023 checking permissions 0.000003 | checking permissions 0.000003 checking permissions 0.000002 | Opening tables 0.000009 | Opening tables 0.000005 init 0.000021 | init 0.000012 System lock 0.000007 | System lock 0.000003 optimizing 0.000007 | optimizing 0.000006 statistics 0.000011 | statistics 0.000006 preparing 0.000009 | preparing 0.000006 optimizing 0.000002 | statistics 0.000003 | preparing 0.000003 | executing 0.000002 | Sending data 0.000037 | executing 0.000002 | executing 0.000001 Sending data 0.010802 | Sending data 0.004614 end 0.000004 | end 0.000003 query end 0.000003 | query end 0.000002 closing tables 0.000005 | closing tables 0.000003 freeing items 0.000011 | freeing items 0.000007 cleaning up 0.000007 | cleaning up 0.000006 Pour tester du code, R et Python fournissent aussi des instructions, respectivement la fonction microbenchmark du package eponyme et la fonction magique %timeit. En voici des exemples d'utilisation : $gh> R > library("microbenchmark") > W <- c(3,8,5,1,8,2) > microbenchmark(W==max(W)) Unit: nanoseconds expr min lq mean median uq max neval W == max(W) 333 344.5 509.04 349 415.5 5768 100 > M <- max(W) > microbenchmark(W==M) Unit: nanoseconds expr min lq mean median uq max neval W == M 157 163 193.64 165 169 2210 100 > # une seule fois ne suffit pas > microbenchmark(W==M) Unit: nanoseconds expr min lq mean median uq max neval W == M 159 165 207.77 166 174 3113 100 > microbenchmark(W==M) Unit: nanoseconds expr min lq mean median uq max neval W == M 160 165 212.55 167 170.5 3471 100 > microbenchmark(W==max(W)) Unit: nanoseconds expr min lq mean median uq max neval W == max(W) 339 344 413.25 362 407 3596 100 > microbenchmark(W==max(W)) Unit: nanoseconds expr min lq mean median uq max neval W == max(W) 337 343.5 411.7 359 403 3561 100 > quit() Save workspace image? [y/n/c]: n $gh> ipython Python 3.5.2 (default, Sep 14 2017, 22:51:06) Type 'copyright', 'credits' or 'license' for more information IPython 6.3.1 -- An enhanced Interactive Python. Type '?' for help. In [1]: import numpy as np In [2]: W = np.array([3,8,5,1,8,2]) In [3]: %timeit W==W.max() 3.54 µs ± 26.5 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each) In [4]: M = W.max() In [5]: %timeit W==M 1.13 µs ± 2.17 ns per loop (mean ± std. dev. of 7 runs, 1000000 loops each) In [6]: %timeit W==M 1.15 µs ± 2.97 ns per loop (mean ± std. dev. of 7 runs, 1000000 loops each) In [7]: # un seul essai, ce n'est sans doute pas suffisant In [8]: %timeit W==M 1.15 µs ± 4.92 ns per loop (mean ± std. dev. of 7 runs, 1000000 loops each) In [9]: %timeit W==W.max() 3.56 µs ± 58.2 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each) In [10]: %timeit W==W.max() 3.57 µs ± 41.6 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each) In [11]: exit Ce qu'on doit retenir de tout cela, c'est principalement deux choses : de nombreuses solutions à des problèmes classiques sont déjà pré-programmées, disponibles et il vaut mieux les utiliser plutôt que de vouloir réinventer la roue et l'eau chaude parce que ces solutions sont robustes ; exécuter une fois le code pour avoir une idée de sa vitesse et de sa durée d'exécution n'est pas suffisant (il peut y avoir de la mise en cache des données, d'autres processus en mémoire...) et il vaut mieux utiliser des outils pour évaluer la performance ; il faut penser à se se poser la question de l'optimisation dès que la taille des données est importante ou dès que le problème risque d'exploser combinatoirement. 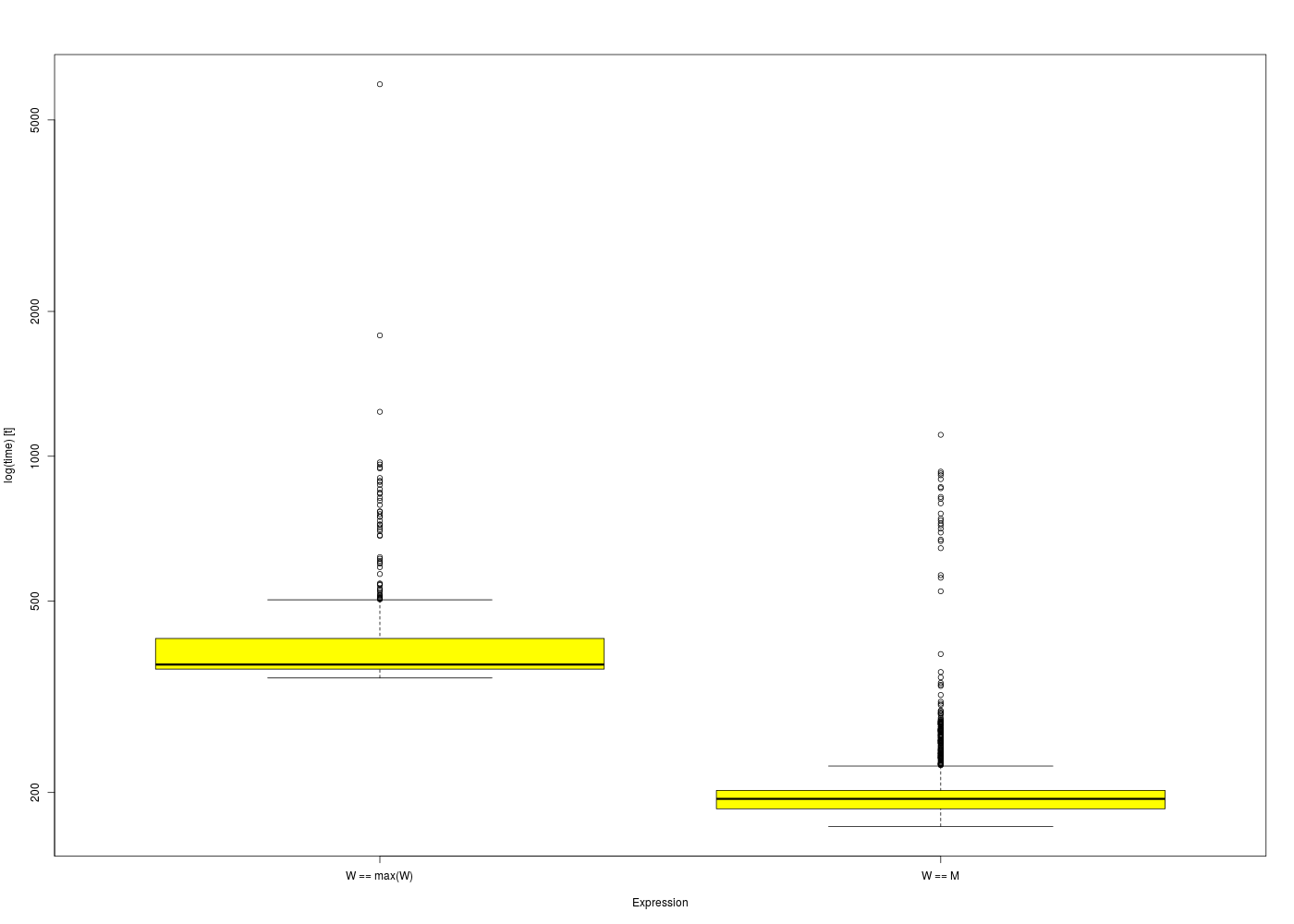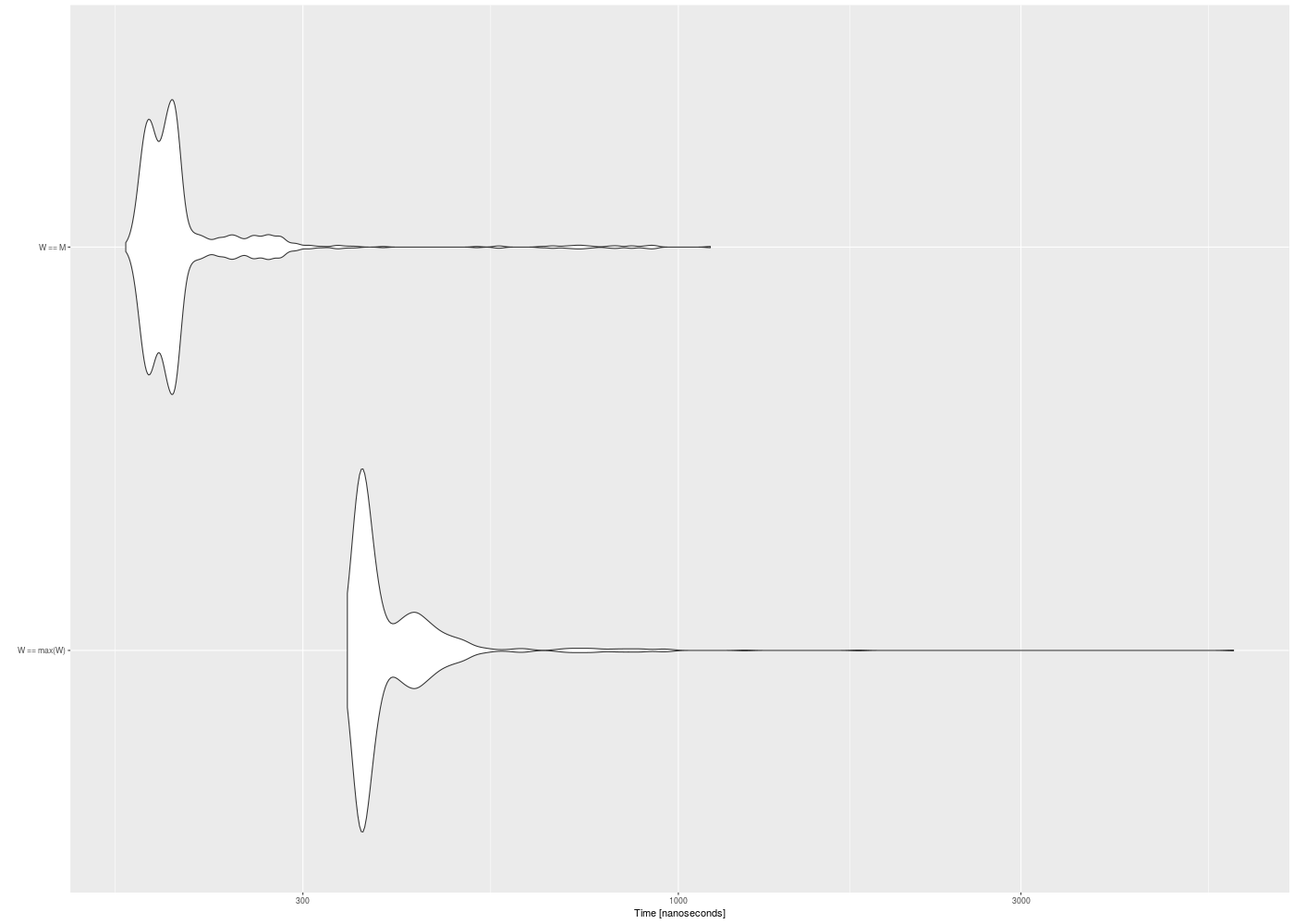Code et graphiques (cliquables) non expliqués : library("microbenchmark") library("ggplot2") # pour autoplot W <- c(3,8,5,1,8,2) M <- max(W) mb <- microbenchmark(W==max(W),W==M,times=1000) png("boxplot-mb.png",width=1400,height=1000) boxplot(mb,col="yellow") dev.off() png("autoplot-mb.png",1400,1000) amb <- autoplot(mb) print(amb) dev.off()                      retour au plan de cours

 

Code-source PHP de cette page ; code Javascript associé.

 

   Retour à la page principale de   (gH)