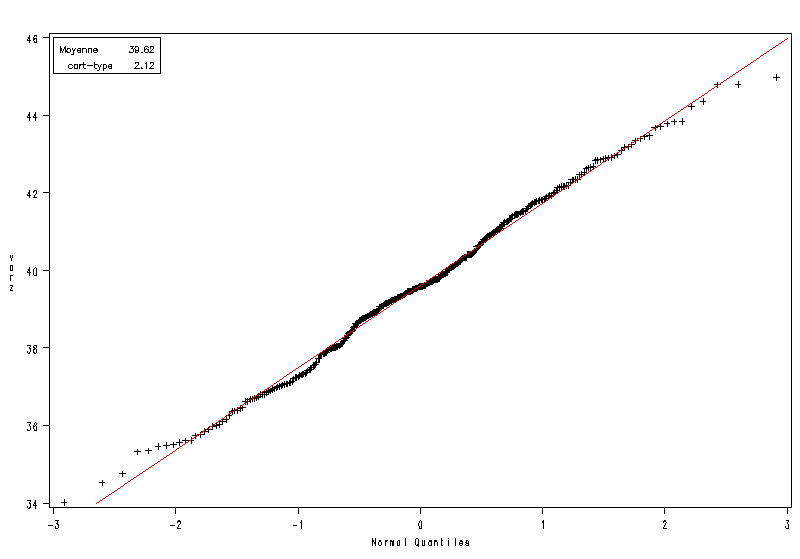
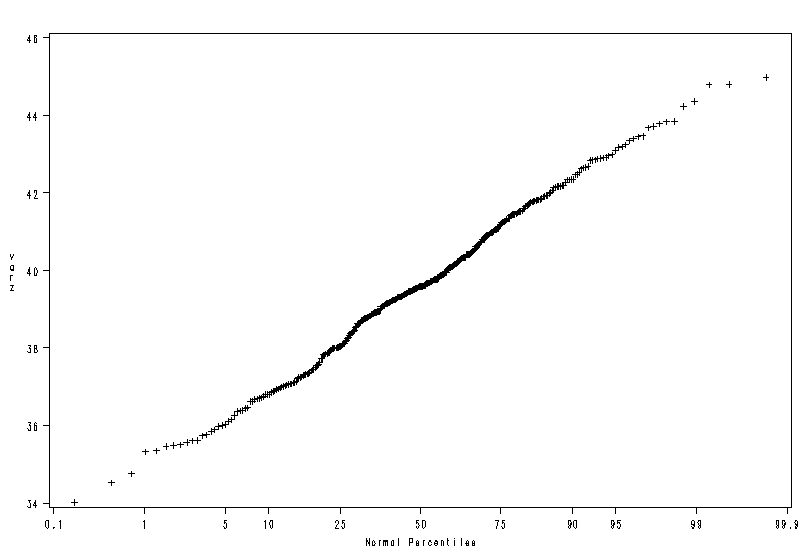
| Le Système SAS |
La procédure UNIVARIATE
Variable : varz
| Moments | |||
|---|---|---|---|
| N | 350 | Somme poids | 350 |
| Moyenne | 39.6186083 | Somme obs. | 13866.5129 |
| Écart-type | 2.12273783 | Variance | 4.50601589 |
| Skewness | 0.00333226 | Kurtosis | -0.4233906 |
| SS non corrigée | 550944.542 | SS corrigée | 1572.59954 |
| Coeff Variation | 5.35793134 | Moy. erreur std | 0.11346511 |
| Mesures statistiques de base | |||
|---|---|---|---|
| Position | Variabilité | ||
| Moyenne | 39.61861 | Écart-type | 2.12274 |
| Médiane | 39.58670 | Variance | 4.50602 |
| Mode | 40.41850 | Étendue | 10.96360 |
| Intervalle interquartile | 3.12950 | ||
| Modes | |
|---|---|
| Mode | Effectif |
| 40.4185 | 2 |
| Intervalles de confiance sous hypothèse de normalité | |||
|---|---|---|---|
| Paramètre | Estimation | 95% Limites de confiance | |
| Moyenne | 39.61861 | 39.39545 | 39.84177 |
| Écart-type | 2.12274 | 1.97627 | 2.29284 |
| Variance | 4.50602 | 3.90563 | 5.25711 |
| Tests de position : Mu0=0 | ||||
|---|---|---|---|---|
| Test | Statistique | p Value | ||
| t de Student | t | 349.17 | Pr > |t| | <.0001 |
| Signe | M | 175 | Pr >= |M| | <.0001 |
| Rangs signés | S | 30712.5 | Pr >= |S| | <.0001 |
| Position : Mu0=0.00 | |
|---|---|
| Effectif | Valeur |
| Num Obs > Mu0 | 350 |
| Num Obs ^= Mu0 | 350 |
| Num Obs < Mu0 | 0 |
| Tests de normalité | ||||
|---|---|---|---|---|
| Test | Statistique | p Value | ||
| Shapiro-Wilk | W | 0.99462 | Pr < W | 0.2589 |
| Kolmogorov-Smirnov | D | 0.032911 | Pr > D | >0.1500 |
| Cramer-von Mises | W-Sq | 0.077971 | Pr > W-Sq | 0.2260 |
| Anderson-Darling | A-Sq | 0.487879 | Pr > A-Sq | 0.2292 |
| Moyennes tronquées | ||||||||
|---|---|---|---|---|---|---|---|---|
| Pourcent. tronqué en queue |
Nombre tronqué en queue |
Moyenne tronquée |
Erreur Std Moyenne tronquée |
95% Limites de confiance | DF | t pour H0: Mu0=0.00 |
Pr > |t| | |
| 25.14 | 88 | 39.62846 | 0.131631 | 39.36866 | 39.88827 | 173 | 301.0581 | <.0001 |
| Winsorized Means | ||||||||
|---|---|---|---|---|---|---|---|---|
| Percent Winsorized in Tail |
Number Winsorized in Tail |
Winsorized Mean |
Std Error Winsorized Mean |
95% Limites de confiance | DF | t for H0: Mu0=0.00 |
Pr > |t| | |
| 25.14 | 88 | 39.61169 | 0.131822 | 39.35150 | 39.87187 | 173 | 300.4943 | <.0001 |
| Mesures d'échelle robustes | ||
|---|---|---|
| Mesure | Valeur | Estimation de Sigma |
| Intervalle interquartile | 3.129500 | 2.319901 |
| Écart à la moyenne de Gini | 2.418313 | 2.143174 |
| MAD | 1.543050 | 2.287726 |
| Sn | 2.126644 | 2.126644 |
| Qn | 2.191460 | 2.167923 |
| Quantiles (Définition 5) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Quantile | Estimation | Statistiques d'ordre | ||||||
| 95% Intervalle de confiance sous hypothèse de normalité |
95% Intervalle de confiance;Distribution libre | Rang LCL | Rang UCL | Coverage | ||||
| 100% Max | 44.9798 | |||||||
| 99% | 44.3637 | 44.15470 | 45.01576 | 43.7829 | 44.9798 | 343 | 350 | 94.43 |
| 95% | 43.0982 | 42.78778 | 43.47351 | 42.8491 | 43.6759 | 325 | 341 | 95.18 |
| 90% | 42.3533 | 42.05362 | 42.65670 | 42.0634 | 42.8506 | 304 | 326 | 95.02 |
| 75% Q3 | 41.1804 | 40.81177 | 41.30650 | 40.8006 | 41.5189 | 247 | 279 | 95.20 |
| 50% Médiane | 39.5867 | 39.39545 | 39.84177 | 39.3921 | 39.7774 | 157 | 194 | 95.22 |
| 25% Q1 | 38.0509 | 37.93072 | 38.42544 | 37.7321 | 38.5490 | 72 | 104 | 95.20 |
| 10% | 36.8099 | 36.58051 | 37.18359 | 36.4417 | 37.0669 | 25 | 47 | 95.02 |
| 5% | 36.0358 | 35.76371 | 36.44944 | 35.6057 | 36.4595 | 10 | 26 | 95.18 |
| 1% | 35.3258 | 34.22146 | 35.08252 | 34.0162 | 35.5024 | 1 | 8 | 94.43 |
| 0% Min | 34.0162 | |||||||
| Observations extrêmes | |||
|---|---|---|---|
| Inférieures | Supérieures | ||
| Valeur | Obs. | Valeur | Obs. |
| 34.0162 | 316 | 44.2364 | 349 |
| 34.5225 | 141 | 44.3637 | 35 |
| 34.7523 | 106 | 44.7942 | 210 |
| 35.3258 | 281 | 44.7954 | 350 |
| 35.3490 | 317 | 44.9798 | 105 |
| Valeurs extrêmes | |||||
|---|---|---|---|---|---|
| Inférieures | Supérieures | ||||
| Ordre | Valeur | Fréq | Ordre | Valeur | Fréq |
| 1 | 34.0162 | 1 | 345 | 44.2364 | 1 |
| 2 | 34.5225 | 1 | 346 | 44.3637 | 1 |
| 3 | 34.7523 | 1 | 347 | 44.7942 | 1 |
| 4 | 35.3258 | 1 | 348 | 44.7954 | 1 |
| 5 | 35.3490 | 1 | 349 | 44.9798 | 1 |
| Nombres d'occurrences | |||
|---|---|---|---|
| Valeur | Effectif | Pourcentages | |
| Cellule | Cum. | ||
| 34.0162 | 1 | 0.3 | 0.3 |
| 34.5225 | 1 | 0.3 | 0.6 |
| 34.7523 | 1 | 0.3 | 0.9 |
| 35.3258 | 1 | 0.3 | 1.1 |
| 35.3490 | 1 | 0.3 | 1.4 |
| 35.4636 | 1 | 0.3 | 1.7 |
| 35.4859 | 1 | 0.3 | 2.0 |
| 35.5024 | 1 | 0.3 | 2.3 |
| 35.5628 | 1 | 0.3 | 2.6 |
| 35.6057 | 1 | 0.3 | 2.9 |
| 35.6207 | 1 | 0.3 | 3.1 |
| 35.7306 | 1 | 0.3 | 3.4 |
| 35.7643 | 1 | 0.3 | 3.7 |
| 35.8541 | 1 | 0.3 | 4.0 |
| 35.8933 | 1 | 0.3 | 4.3 |
| 35.9865 | 1 | 0.3 | 4.6 |
| 36.0078 | 1 | 0.3 | 4.9 |
| 36.0358 | 1 | 0.3 | 5.1 |
| 36.1065 | 1 | 0.3 | 5.4 |
| 36.1454 | 1 | 0.3 | 5.7 |
| 36.2623 | 1 | 0.3 | 6.0 |
| 36.3617 | 1 | 0.3 | 6.3 |
| 36.3757 | 1 | 0.3 | 6.6 |
| 36.3990 | 1 | 0.3 | 6.9 |
| 36.4417 | 1 | 0.3 | 7.1 |
| 36.4595 | 1 | 0.3 | 7.4 |
| 36.6201 | 1 | 0.3 | 7.7 |
| 36.6301 | 1 | 0.3 | 8.0 |
| 36.6792 | 1 | 0.3 | 8.3 |
| 36.6896 | 1 | 0.3 | 8.6 |
| 36.6973 | 1 | 0.3 | 8.9 |
| 36.7148 | 1 | 0.3 | 9.1 |
| 36.7528 | 1 | 0.3 | 9.4 |
| 36.8067 | 1 | 0.3 | 9.7 |
| 36.8087 | 1 | 0.3 | 10.0 |
| 36.8110 | 1 | 0.3 | 10.3 |
| 36.8508 | 1 | 0.3 | 10.6 |
| 36.8782 | 1 | 0.3 | 10.9 |
| 36.8944 | 1 | 0.3 | 11.1 |
| 36.9409 | 1 | 0.3 | 11.4 |
| 36.9515 | 1 | 0.3 | 11.7 |
| 36.9779 | 1 | 0.3 | 12.0 |
| 37.0036 | 1 | 0.3 | 12.3 |
| 37.0156 | 1 | 0.3 | 12.6 |
| 37.0230 | 1 | 0.3 | 12.9 |
| 37.0481 | 1 | 0.3 | 13.1 |
| 37.0669 | 1 | 0.3 | 13.4 |
| 37.0713 | 1 | 0.3 | 13.7 |
| 37.0800 | 1 | 0.3 | 14.0 |
| 37.1052 | 1 | 0.3 | 14.3 |
| 37.1107 | 1 | 0.3 | 14.6 |
| 37.1417 | 1 | 0.3 | 14.9 |
| 37.1998 | 1 | 0.3 | 15.1 |
| 37.2403 | 1 | 0.3 | 15.4 |
| 37.2481 | 1 | 0.3 | 15.7 |
| 37.2534 | 1 | 0.3 | 16.0 |
| 37.2904 | 1 | 0.3 | 16.3 |
| 37.3100 | 1 | 0.3 | 16.6 |
| 37.3210 | 1 | 0.3 | 16.9 |
| 37.3394 | 1 | 0.3 | 17.1 |
| 37.3485 | 1 | 0.3 | 17.4 |
| 37.3742 | 1 | 0.3 | 17.7 |
| 37.4134 | 1 | 0.3 | 18.0 |
| 37.4401 | 1 | 0.3 | 18.3 |
| 37.4439 | 1 | 0.3 | 18.6 |
| 37.4871 | 1 | 0.3 | 18.9 |
| 37.5407 | 1 | 0.3 | 19.1 |
| 37.5535 | 1 | 0.3 | 19.4 |
| 37.5790 | 1 | 0.3 | 19.7 |
| 37.6360 | 1 | 0.3 | 20.0 |
| 37.7281 | 1 | 0.3 | 20.3 |
| 37.7321 | 1 | 0.3 | 20.6 |
| 37.8216 | 1 | 0.3 | 20.9 |
| 37.8278 | 1 | 0.3 | 21.1 |
| 37.8501 | 1 | 0.3 | 21.4 |
| 37.8554 | 1 | 0.3 | 21.7 |
| 37.8778 | 1 | 0.3 | 22.0 |
| 37.8890 | 1 | 0.3 | 22.3 |
| 37.9367 | 1 | 0.3 | 22.6 |
| 37.9587 | 1 | 0.3 | 22.9 |
| 37.9894 | 1 | 0.3 | 23.1 |
| 37.9975 | 1 | 0.3 | 23.4 |
| 38.0080 | 1 | 0.3 | 23.7 |
| 38.0101 | 1 | 0.3 | 24.0 |
| 38.0180 | 1 | 0.3 | 24.3 |
| 38.0222 | 1 | 0.3 | 24.6 |
| 38.0470 | 1 | 0.3 | 24.9 |
| 38.0509 | 1 | 0.3 | 25.1 |
| 38.0571 | 1 | 0.3 | 25.4 |
| 38.0865 | 1 | 0.3 | 25.7 |
| 38.1230 | 1 | 0.3 | 26.0 |
| 38.1258 | 1 | 0.3 | 26.3 |
| 38.1759 | 1 | 0.3 | 26.6 |
| 38.1871 | 1 | 0.3 | 26.9 |
| 38.2456 | 1 | 0.3 | 27.1 |
| 38.2795 | 1 | 0.3 | 27.4 |
| 38.3130 | 1 | 0.3 | 27.7 |
| 38.3682 | 1 | 0.3 | 28.0 |
| 38.3961 | 1 | 0.3 | 28.3 |
| 38.4146 | 1 | 0.3 | 28.6 |
| 38.4267 | 1 | 0.3 | 28.9 |
| 38.4388 | 1 | 0.3 | 29.1 |
| 38.5335 | 1 | 0.3 | 29.4 |
| 38.5490 | 1 | 0.3 | 29.7 |
| 38.6214 | 1 | 0.3 | 30.0 |
| 38.6317 | 1 | 0.3 | 30.3 |
| 38.6372 | 1 | 0.3 | 30.6 |
| 38.6671 | 1 | 0.3 | 30.9 |
| 38.7102 | 1 | 0.3 | 31.1 |
| 38.7199 | 1 | 0.3 | 31.4 |
| 38.7413 | 1 | 0.3 | 31.7 |
| 38.7592 | 1 | 0.3 | 32.0 |
| 38.7597 | 1 | 0.3 | 32.3 |
| 38.7807 | 1 | 0.3 | 32.6 |
| 38.7880 | 1 | 0.3 | 32.9 |
| 38.8074 | 1 | 0.3 | 33.1 |
| 38.8256 | 1 | 0.3 | 33.4 |
| 38.8272 | 1 | 0.3 | 33.7 |
| 38.8551 | 1 | 0.3 | 34.0 |
| 38.8637 | 1 | 0.3 | 34.3 |
| 38.8806 | 1 | 0.3 | 34.6 |
| 38.8970 | 1 | 0.3 | 34.9 |
| 38.9167 | 1 | 0.3 | 35.1 |
| 38.9202 | 1 | 0.3 | 35.4 |
| 38.9280 | 1 | 0.3 | 35.7 |
| 38.9452 | 1 | 0.3 | 36.0 |
| 38.9466 | 1 | 0.3 | 36.3 |
| 38.9540 | 1 | 0.3 | 36.6 |
| 38.9794 | 1 | 0.3 | 36.9 |
| 39.0616 | 1 | 0.3 | 37.1 |
| 39.0625 | 1 | 0.3 | 37.4 |
| 39.0820 | 1 | 0.3 | 37.7 |
| 39.0862 | 1 | 0.3 | 38.0 |
| 39.0907 | 1 | 0.3 | 38.3 |
| 39.1362 | 1 | 0.3 | 38.6 |
| 39.1508 | 1 | 0.3 | 38.9 |
| 39.1606 | 1 | 0.3 | 39.1 |
| 39.1677 | 1 | 0.3 | 39.4 |
| 39.1847 | 1 | 0.3 | 39.7 |
| 39.1909 | 1 | 0.3 | 40.0 |
| 39.1939 | 1 | 0.3 | 40.3 |
| 39.2154 | 1 | 0.3 | 40.6 |
| 39.2349 | 1 | 0.3 | 40.9 |
| 39.2386 | 1 | 0.3 | 41.1 |
| 39.2409 | 1 | 0.3 | 41.4 |
| 39.2511 | 1 | 0.3 | 41.7 |
| 39.2681 | 1 | 0.3 | 42.0 |
| 39.2689 | 1 | 0.3 | 42.3 |
| 39.3053 | 1 | 0.3 | 42.6 |
| 39.3201 | 1 | 0.3 | 42.9 |
| 39.3217 | 1 | 0.3 | 43.1 |
| 39.3226 | 1 | 0.3 | 43.4 |
| 39.3281 | 1 | 0.3 | 43.7 |
| 39.3433 | 1 | 0.3 | 44.0 |
| 39.3458 | 1 | 0.3 | 44.3 |
| 39.3696 | 1 | 0.3 | 44.6 |
| 39.3921 | 1 | 0.3 | 44.9 |
| 39.4004 | 1 | 0.3 | 45.1 |
| 39.4162 | 1 | 0.3 | 45.4 |
| 39.4212 | 1 | 0.3 | 45.7 |
| 39.4576 | 1 | 0.3 | 46.0 |
| 39.4591 | 1 | 0.3 | 46.3 |
| 39.4665 | 1 | 0.3 | 46.6 |
| 39.4666 | 1 | 0.3 | 46.9 |
| 39.4757 | 1 | 0.3 | 47.1 |
| 39.4909 | 1 | 0.3 | 47.4 |
| 39.5085 | 1 | 0.3 | 47.7 |
| 39.5130 | 1 | 0.3 | 48.0 |
| 39.5233 | 1 | 0.3 | 48.3 |
| 39.5331 | 1 | 0.3 | 48.6 |
| 39.5426 | 1 | 0.3 | 48.9 |
| 39.5479 | 1 | 0.3 | 49.1 |
| 39.5734 | 1 | 0.3 | 49.4 |
| 39.5853 | 1 | 0.3 | 49.7 |
| 39.5854 | 1 | 0.3 | 50.0 |
| 39.5880 | 1 | 0.3 | 50.3 |
| 39.5890 | 1 | 0.3 | 50.6 |
| 39.5954 | 1 | 0.3 | 50.9 |
| 39.6072 | 1 | 0.3 | 51.1 |
| 39.6107 | 1 | 0.3 | 51.4 |
| 39.6136 | 1 | 0.3 | 51.7 |
| 39.6538 | 1 | 0.3 | 52.0 |
| 39.6664 | 1 | 0.3 | 52.3 |
| 39.6688 | 1 | 0.3 | 52.6 |
| 39.6805 | 1 | 0.3 | 52.9 |
| 39.6809 | 1 | 0.3 | 53.1 |
| 39.7160 | 1 | 0.3 | 53.4 |
| 39.7176 | 1 | 0.3 | 53.7 |
| 39.7281 | 1 | 0.3 | 54.0 |
| 39.7387 | 1 | 0.3 | 54.3 |
| 39.7612 | 1 | 0.3 | 54.6 |
| 39.7699 | 1 | 0.3 | 54.9 |
| 39.7753 | 1 | 0.3 | 55.1 |
| 39.7774 | 1 | 0.3 | 55.4 |
| 39.7775 | 1 | 0.3 | 55.7 |
| 39.8012 | 1 | 0.3 | 56.0 |
| 39.8016 | 1 | 0.3 | 56.3 |
| 39.8436 | 1 | 0.3 | 56.6 |
| 39.8824 | 1 | 0.3 | 56.9 |
| 39.8879 | 1 | 0.3 | 57.1 |
| 39.9009 | 1 | 0.3 | 57.4 |
| 39.9060 | 1 | 0.3 | 57.7 |
| 39.9127 | 1 | 0.3 | 58.0 |
| 39.9345 | 1 | 0.3 | 58.3 |
| 39.9447 | 1 | 0.3 | 58.6 |
| 39.9510 | 1 | 0.3 | 58.9 |
| 40.0266 | 1 | 0.3 | 59.1 |
| 40.0576 | 1 | 0.3 | 59.4 |
| 40.0639 | 1 | 0.3 | 59.7 |
| 40.0749 | 1 | 0.3 | 60.0 |
| 40.0780 | 1 | 0.3 | 60.3 |
| 40.0920 | 1 | 0.3 | 60.6 |
| 40.1041 | 1 | 0.3 | 60.9 |
| 40.1265 | 1 | 0.3 | 61.1 |
| 40.1462 | 1 | 0.3 | 61.4 |
| 40.1723 | 1 | 0.3 | 61.7 |
| 40.1770 | 1 | 0.3 | 62.0 |
| 40.2026 | 1 | 0.3 | 62.3 |
| 40.2411 | 1 | 0.3 | 62.6 |
| 40.2421 | 1 | 0.3 | 62.9 |
| 40.2483 | 1 | 0.3 | 63.1 |
| 40.2859 | 1 | 0.3 | 63.4 |
| 40.3184 | 1 | 0.3 | 63.7 |
| 40.3296 | 1 | 0.3 | 64.0 |
| 40.3323 | 1 | 0.3 | 64.3 |
| 40.3332 | 1 | 0.3 | 64.6 |
| 40.3387 | 1 | 0.3 | 64.9 |
| 40.4101 | 1 | 0.3 | 65.1 |
| 40.4121 | 1 | 0.3 | 65.4 |
| 40.4185 | 2 | 0.6 | 66.0 |
| 40.4189 | 1 | 0.3 | 66.3 |
| 40.4324 | 1 | 0.3 | 66.6 |
| 40.4741 | 1 | 0.3 | 66.9 |
| 40.5005 | 1 | 0.3 | 67.1 |
| 40.5033 | 1 | 0.3 | 67.4 |
| 40.5395 | 1 | 0.3 | 67.7 |
| 40.6096 | 1 | 0.3 | 68.0 |
| 40.6238 | 1 | 0.3 | 68.3 |
| 40.6306 | 1 | 0.3 | 68.6 |
| 40.6490 | 1 | 0.3 | 68.9 |
| 40.6672 | 1 | 0.3 | 69.1 |
| 40.7276 | 1 | 0.3 | 69.4 |
| 40.7483 | 1 | 0.3 | 69.7 |
| 40.7859 | 1 | 0.3 | 70.0 |
| 40.7968 | 1 | 0.3 | 70.3 |
| 40.8006 | 1 | 0.3 | 70.6 |
| 40.8602 | 1 | 0.3 | 70.9 |
| 40.8846 | 1 | 0.3 | 71.1 |
| 40.9096 | 1 | 0.3 | 71.4 |
| 40.9163 | 1 | 0.3 | 71.7 |
| 40.9471 | 1 | 0.3 | 72.0 |
| 40.9668 | 1 | 0.3 | 72.3 |
| 40.9687 | 1 | 0.3 | 72.6 |
| 40.9843 | 1 | 0.3 | 72.9 |
| 41.0143 | 1 | 0.3 | 73.1 |
| 41.0532 | 1 | 0.3 | 73.4 |
| 41.0549 | 1 | 0.3 | 73.7 |
| 41.0596 | 1 | 0.3 | 74.0 |
| 41.0845 | 1 | 0.3 | 74.3 |
| 41.0901 | 1 | 0.3 | 74.6 |
| 41.1331 | 1 | 0.3 | 74.9 |
| 41.1804 | 1 | 0.3 | 75.1 |
| 41.2328 | 1 | 0.3 | 75.4 |
| 41.2458 | 1 | 0.3 | 75.7 |
| 41.2556 | 1 | 0.3 | 76.0 |
| 41.2679 | 1 | 0.3 | 76.3 |
| 41.2764 | 1 | 0.3 | 76.6 |
| 41.3162 | 1 | 0.3 | 76.9 |
| 41.3316 | 1 | 0.3 | 77.1 |
| 41.3345 | 1 | 0.3 | 77.4 |
| 41.4093 | 1 | 0.3 | 77.7 |
| 41.4415 | 1 | 0.3 | 78.0 |
| 41.4461 | 1 | 0.3 | 78.3 |
| 41.4531 | 1 | 0.3 | 78.6 |
| 41.4554 | 1 | 0.3 | 78.9 |
| 41.4611 | 1 | 0.3 | 79.1 |
| 41.4910 | 1 | 0.3 | 79.4 |
| 41.5189 | 1 | 0.3 | 79.7 |
| 41.5219 | 1 | 0.3 | 80.0 |
| 41.5253 | 1 | 0.3 | 80.3 |
| 41.5414 | 1 | 0.3 | 80.6 |
| 41.5947 | 1 | 0.3 | 80.9 |
| 41.6032 | 1 | 0.3 | 81.1 |
| 41.6538 | 1 | 0.3 | 81.4 |
| 41.6827 | 1 | 0.3 | 81.7 |
| 41.7053 | 1 | 0.3 | 82.0 |
| 41.7270 | 1 | 0.3 | 82.3 |
| 41.7602 | 1 | 0.3 | 82.6 |
| 41.7670 | 1 | 0.3 | 82.9 |
| 41.7849 | 1 | 0.3 | 83.1 |
| 41.8026 | 1 | 0.3 | 83.4 |
| 41.8096 | 1 | 0.3 | 83.7 |
| 41.8239 | 1 | 0.3 | 84.0 |
| 41.8240 | 1 | 0.3 | 84.3 |
| 41.8312 | 1 | 0.3 | 84.6 |
| 41.8666 | 1 | 0.3 | 84.9 |
| 41.8988 | 1 | 0.3 | 85.1 |
| 41.9062 | 1 | 0.3 | 85.4 |
| 41.9416 | 1 | 0.3 | 85.7 |
| 41.9448 | 1 | 0.3 | 86.0 |
| 41.9925 | 1 | 0.3 | 86.3 |
| 42.0226 | 1 | 0.3 | 86.6 |
| 42.0634 | 1 | 0.3 | 86.9 |
| 42.1264 | 1 | 0.3 | 87.1 |
| 42.1484 | 1 | 0.3 | 87.4 |
| 42.1647 | 1 | 0.3 | 87.7 |
| 42.1750 | 1 | 0.3 | 88.0 |
| 42.1764 | 1 | 0.3 | 88.3 |
| 42.1984 | 1 | 0.3 | 88.6 |
| 42.2005 | 1 | 0.3 | 88.9 |
| 42.2646 | 1 | 0.3 | 89.1 |
| 42.3396 | 1 | 0.3 | 89.4 |
| 42.3423 | 1 | 0.3 | 89.7 |
| 42.3505 | 1 | 0.3 | 90.0 |
| 42.3560 | 1 | 0.3 | 90.3 |
| 42.4650 | 1 | 0.3 | 90.6 |
| 42.4788 | 1 | 0.3 | 90.9 |
| 42.5292 | 1 | 0.3 | 91.1 |
| 42.6217 | 1 | 0.3 | 91.4 |
| 42.6517 | 1 | 0.3 | 91.7 |
| 42.6636 | 1 | 0.3 | 92.0 |
| 42.6859 | 1 | 0.3 | 92.3 |
| 42.8392 | 1 | 0.3 | 92.6 |
| 42.8491 | 1 | 0.3 | 92.9 |
| 42.8506 | 1 | 0.3 | 93.1 |
| 42.8790 | 1 | 0.3 | 93.4 |
| 42.8999 | 1 | 0.3 | 93.7 |
| 42.9026 | 1 | 0.3 | 94.0 |
| 42.9181 | 1 | 0.3 | 94.3 |
| 42.9545 | 1 | 0.3 | 94.6 |
| 42.9828 | 1 | 0.3 | 94.9 |
| 43.0982 | 1 | 0.3 | 95.1 |
| 43.1701 | 1 | 0.3 | 95.4 |
| 43.1870 | 1 | 0.3 | 95.7 |
| 43.2455 | 1 | 0.3 | 96.0 |
| 43.3478 | 1 | 0.3 | 96.3 |
| 43.3932 | 1 | 0.3 | 96.6 |
| 43.4467 | 1 | 0.3 | 96.9 |
| 43.4677 | 1 | 0.3 | 97.1 |
| 43.6759 | 1 | 0.3 | 97.4 |
| 43.7229 | 1 | 0.3 | 97.7 |
| 43.7829 | 1 | 0.3 | 98.0 |
| 43.8318 | 1 | 0.3 | 98.3 |
| 43.8531 | 1 | 0.3 | 98.6 |
| 44.2364 | 1 | 0.3 | 98.9 |
| 44.3637 | 1 | 0.3 | 99.1 |
| 44.7942 | 1 | 0.3 | 99.4 |
| 44.7954 | 1 | 0.3 | 99.7 |
| 44.9798 | 1 | 0.3 | 100.0 |
| Le Système SAS |
La procédure UNIVARIATE
Variable : varz
Stem Leaf # Boîte
45 0 1 |
44 88 2 |
44 24 2 |
43 577889 6 |
43 001222344 9 |
42 55567778899999 14 |
42 001112222233344 15 |
41 555555556677778888888899999 27 |
41 0000111111222333333444 22 +-----+
40 5555666677788899999 19 | |
40 0011111111222222333333444444 28 | |
39 555555555555666666666777777777888888889999999 45 *--+--*
39 001111112222222222333333333344444 33 | |
38 5566677778888888999999999 25 | |
38 00000000111112223344444 23 +-----+
37 55666778899999 14 |
37 0000001111112223333334444 25 |
36 566777788889999 15 |
36 0001134444 10 |
35 5556667899 10 |
35 33 2 |
34 58 2 |
34 0 1 |
----+----+----+----+----+----+----+----+----+
Courbe de probabilité normale
45.25+
| +**
| +**
| ***
| ****
| ****
| ***
| ****
| ***
| ***
| ***
39.75+ ****
| ***
| ***
| **
| ***
| ****
| ***
| ***
| ****
| ***+
|**++
34.25+*
+----+----+----+----+----+----+----+----+----+----+
-2 -1 0 +1 +2
|
La procédure UNIVARIATE
Variable : varz
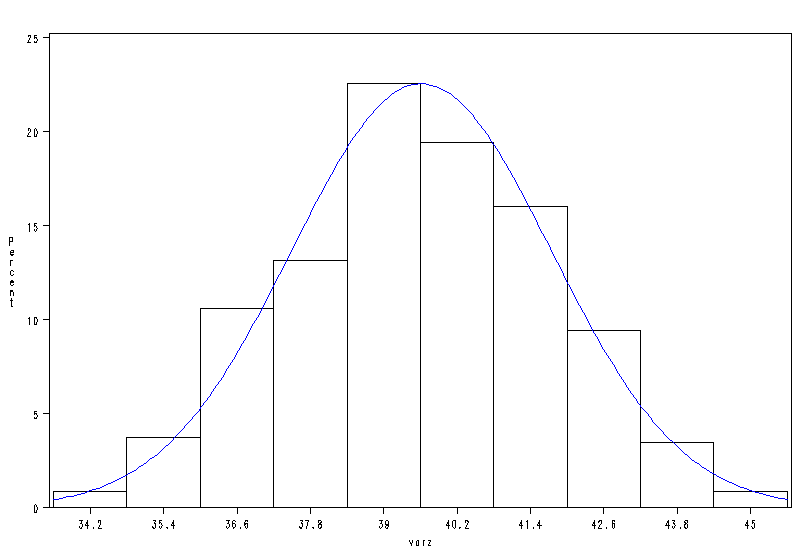
| Le Système SAS |
La procédure UNIVARIATE
Fitted Distribution for varz
| Parameters for Normal Distribution | ||
|---|---|---|
| Paramètre | Symbole | Estimation |
| Mean | Mu | 39.61861 |
| Std Dev | Sigma | 2.122738 |
| Goodness-of-Fit Tests for Normal Distribution | ||||
|---|---|---|---|---|
| Test | Statistique | p Value | ||
| Kolmogorov-Smirnov | D | 0.03291063 | Pr > D | >0.150 |
| Cramer-von Mises | W-Sq | 0.07797141 | Pr > W-Sq | 0.226 |
| Anderson-Darling | A-Sq | 0.48787876 | Pr > A-Sq | 0.229 |
| Quantiles for Normal Distribution | ||
|---|---|---|
| Pourcentage | Quantile | |
| Observé | Estimé | |
| 1.0 | 35.3258 | 34.6804 |
| 5.0 | 36.0358 | 36.1270 |
| 10.0 | 36.8099 | 36.8982 |
| 25.0 | 38.0509 | 38.1868 |
| 50.0 | 39.5867 | 39.6186 |
| 75.0 | 41.1804 | 41.0504 |
| 90.0 | 42.3533 | 42.3390 |
| 95.0 | 43.0982 | 43.1102 |
| 99.0 | 44.3637 | 44.5568 |