Introduction à la programmation avec R                 gilles.hunault "at" univ-angers.fr   Ce tuteur se compose de 9 parties :   Partie 1 : Présentation des cours et principes généraux Partie 2 : Affectations, structures de données et affichages Partie 3 : Conditions logiques et tests Partie 4 : Boucles et itérations Partie 5 : Sous-programmes : les fonctions Partie 6 : Eviter de programmer en R Partie 7 : Programmation soutenue Partie 8 : Déboggage, profilage et optimisation Partie 9 : Différences entre programmation et développement     Partie 1 - Présentation des cours et principes généraux   Table des matières cliquable   1. Qu'est-ce que la programmation en R ?   2. Comment apprendre à programmer ?   3. Présentation des cours   4. Principes de programmation   5. Spécificités du langage R 1. Qu'est-ce que la programmation en R ? Programmer, c'est, historiquement «écrire» des programmes, c'est-à-dire des textes dans un langage spécial compris par un ordinateur. Ecrire est mis ici pour réaliser, ce qui signifie à la fois concevoir, écrire, tester, documenter. Lorsqu'un programme est d'importance (penser à un programme qui gère le décollage des avions dans un aéroport), plusieurs personnes voire plusieurs centaines de personnes peuvent y participer. L'expression langage spécial indique qu'il va falloir en quelque sorte apprendre une nouvelle langue, simplifiée (basée plus ou moins sur l'anglais) et surtout, qu'il va falloir tout dire en utilisant cette langue. On utilise parfois un autre langage moins spécifique nommé algorithmique en français pour juste réfléchir aux idées, aux concepts et aux actions à exécuter. Dans un langage de programmation, on trouve en général cinq actions principales  effectuer un calcul (plus ou moins complexe) lire une ou plusieurs valeurs (au clavier, dans un fichier, en mémoire...) écrire une ou plusieurs valeurs (à l'écran, dans un fichier, en mémoire...) appeler un sous-programme (avec éventuellement des paramètres) gérer le flux des instructions (faire des tests ou des boucles) La programmation en R est un peu spéciale dans la mesure où on n'écrit pas vraiment des programmes mais plutôt des scripts dans un environnement. Nous reviendrons régulièrement sur cette différence au travers d'exemples afin que vous puissiez aussi programmer dans d'autres langages. 2. Comment apprendre à programmer ? Pour apprendre à programmer, il faut donc utiliser les mêmes techniques que pour apprendre une nouvelle langue. Cela inclut donc beaucoup de pratique, de répétition, d'entrainement. Après avoir maitrisé le vocabulaire de base, on passe à la syntaxe élémentaire puis au bout d'un certain temps on passe à des phrases plus longues, on apprend la grammaire et surtout, on continue encore et encore... L'avantage avec l'ordinateur, c'est qu'il est infiniment patient et qu'on ne risque pas de l'énerver en commettant toujours la même erreur, qu'on peut essayer et essayer encore et encore, jusqu'à temps qu'on arrive à se faire comprendre. Par contre, le gros défaut, c'est qu'il est bête ou plus exactement mécanique et qu'il est incapable d'accepter l'à peu près. Par exemple si un étranger vous dit «je voudrais un papier blanche» ou «je voudrais une blanche papier» vous corrigerez de vous-mêmes en papier blanc et vous comprendrez ce que veut la personne. Si par contre vous demandez à l'ordinateur d'appeler le sous-programme CALCUL(x,)y au lieu du sous-programme CALCUL(x,y), il ne saura que vous répondre "erreur de syntaxe, " et peut-être, dans le meilleur des cas, "variable manquante après la virgule". 3. Présentation des cours Nous allons donc progressivement apprendre des mots et les utiliser dans des phrases courtes, puis réfléchir pour savoir comment construire des phrases longues, produire automatiquement des séries de phrases, automatiser des comportements... Une des difficultés sera de comprendre comment l'ordinateur comprend nos phrases, de mettre en place des automatismes, des habitudes de programmation. Le cours 1 (ce cours) insiste sur les principes généraux et doit convaincre des qualités qu'il faut développer pour savoir programmer. Le cours 2 sera focalisé sur la notion de variable et d'affectation (calcul ou remplacement de variable). Le cours 3 sert à apprendre comment indiquer à l'ordinateur quelles instructions réaliser en fonction de conditions sur les valeurs des variables (ce qu'on nomme tests logiques). Les boucles et itérations seront présentées au cours 4 alors que les sous-programmes seront traités dans le cours 5. Les autres cours serviront à indiquer tout le travail qu'il reste à faire pour savoir "bien" programmer en R. 4. Principes de programmation Avant de rentrer dans le détail des instructions de programmation, voici quelques exemples de situation pour expliciter les grands principes de la programmation. Vous en déduirez facilement les qualités et compétences requises pour savoir programmer... 4.1 Programmer, c'est réfléchir et organiser Imaginons que nous cherchions ce qu'on nomme maximum d'une série de valeurs, c'est-à-dire la plus grande valeur. Prenons par exemple les valeurs 1 8 2 5 8 7 8. Je suis sûr que vous avez trouvé le maximum qui est 8. Mais de quel 8 s'agit-il ? Est-ce le premier ? Le second ? Le dernier ? Et comment avez-vous fait ? Avez-vous passé en revue toutes les valeurs à partir du début ? Ou à partir de la fin ? Et s'il s'agissait de pourcentages, vu que le maximum est 100 %, est-ce que cela changerait quelque chose à votre façon de chercher le maximum ? Imaginons maintenant que nous voulions le maximum, le nombre de fois où il apparait et la (ou les) positions où il apparait. Sachant que la liste des valeurs est longue pour un humain (disons une centaine de valeurs), sauriez-vous résoudre ce problème en ne passant en revue la liste qu'une seule fois ? Programmer, c'est aussi se poser ce genre de questions. En cas de très grandes listes pour l'ordinateur (par exemple si chaque valeur est obtenue au bout d'un long calcul), il faut réfléchir pour trouver une méthode rapide. Passer en revue la liste une première fois pour trouver le maximum et la passer en revue une seconde fois pour calculer le nombre d'occurences et les positions du maximum est une méthode simple mais non rapide. L'usage veut donc qu'avant de commencer à programmer on réfléchisse au problème, aux entrées et aux sorties, aux fonctionnalités de ce qu'on veut faire, aux durées possibles et prévoir en retour ce qu'on va programmer... 4.2 Programmer, c'est choisir et expliciter ses choix Voici un exemple classique qui fait partie de la programmation traditionnelle : construire le nom d'un fichier de sortie à partir d'un fichier d'entrée. Par exemple on veut, à partir du fichier serie35.xls construire le fichier serie35.txt ou encore, à partir de serie_1.manip2.rep036.xls construire serie_1.manip2.rep036.txt. Vous voyez certainement ce qu'il faut faire : repérer le "bon" point qui indique la fin du nom de fichier (ce n'est donc pas le premier point qu'on rencontre dans le nom de fichier, mais plutôt le dernier), puis extraire la partie avant ce point et rajouter txt ou .txt suivant qu'on a déjà extrait le point ou non. Si les méthodes extraire la première partie avec le point et sans le point sont sans doute équivalentes en terme de simplicité et de vitesse, quelle est la meilleure méthode ? Et selon quels critères ? Une fois que vous aurez trouvé ce qui est la meilleure méthode pour vous (et vos fichiers) -- ce qui n'est peut-être pas la même meilleure méthode que pour vos collègues -- il faut le noter, documenter ce choix pour éviter de se poser la question à nouveau et toujours s'y tenir, ce qui peut se faire en écrivant un sous-programme qui réalise ce traitement. 4.3 Programmer, c'est tester, prévoir et valider Reprenons l'exemple précédent de construction d'un nom de fichier en sortie. Nous avions basé notre analyse sur le fait qu'il y avait un point en fin de nom de fichier d'entrée. Et si ce n'était pas le cas ? C'est ce qui risque d'arriver non pas en ligne, si on tape le nom du fichier, mais si le nom du fichier d'entrée a par exemple été mal construit par un autre programme. Que fait la méthode précédente ? La réponse dépend de la façon dont vous avez détecté le point. Certaines fonctions renvoient, lorsque le point n'est pas trouvé, la valeur -1, d'autres une valeur égale à "1 de plus que la longueur du nom de fichier". Ces deux choix se valent, le plus important est d'y avoir pensé car ce qu'il faut faire dans ce cas dépend de la valeur renvoyée. Nous essaierons, dans le cadre des exercices présentés, de prévoir les cas usuels classiques d'erreur (fichier non présent ou faute de frappe, liste vide de valeurs...) afin d'avoir des programmes dits robustes et fiables. Cela signifie qu'en conséquence il faudra tester différents cas classiques afin de valider le "bon" comportement de nos programmes dans les conditions normales d'application et de gérer les cas exceptionnels. En particulier, il faudra réfléchir, organiser et prévoir ce qu'on fait par exemple si un fichier n'est pas vu alors qu'on traite une liste de fichiers. Interrompre le programme pour demander un nouveau nom est peut-être inadapté, tout arrêter est sans doute trop brutal, se contenter d'afficher un message d'erreur est certainement maladroit parce qu'il risque de disparaitre si la liste des fichiers à traiter est longue... 4.4 Programmer demande de l'endurance, de la précision et de la rigueur Au vu des situations présentées ci-dessus, il est clair que la programmation n'est pas au départ une partie de plaisir puisqu'il faut réfléchir, trouver une "bonne" solution -- souvent un compromis entre simplicité et vitesse d'exécution, penser aux erreurs possibles... Par contre, c'est au final une réelle joie que d'avoir un programme qui "tourne" sans "bugger" ou "boucler", que d'obtenir presque automatiquement toute une série de résultats et de fichiers sans avoir de nombreux copier/coller ou de fastidieuses manipulations à faire et à refaire, de fournir à la communauté un programme qui peut aider d'autres collègues et faire gagner ainsi beaucoup de temps, cette denrée rare... 5. Spécificités du langage R La programmation en R ressemble au départ à la programmation traditionnelle. Ce qui change beaucoup, c'est principalement le fait que R est vectoriel, qu'on utilise un environnement qui sauvegarde les variables et qu'il y a des milliers de fonctions de base et des milliers de fonctions complémentaires disponibles dans des packages. Du coup, de nombreuses actions (trier, calculer, tracer...) sont soit élémentaires soit déjà programmées.   Partie 2 - Affectations, structures de données et affichages   Table des matières cliquable   1. Variables simples et affectations   2. Structures de données et affectations en R   3. Autres "objets" en R   4. Affichage des variables en R   5. Spécificités du langage R 1. Variables simples et affectations Une variable est semblable à une boite dotée d'un nom (ou identifiant) qui contient une valeur (nommée aussi contenu de la variable). Réaliser une affectation, c'est mettre une valeur dans une variable, qu'il s'agisse d'une valeur numérique ou caractère ou autre. Mettre une valeur dans une variable pour la première fois se nomme initialiser la variable. Contrairement à d'autres langages de programmation il n'y a pas besoin en R de prévenir ("déclarer" ou "typer" cette variable) en prévenant ce qu'elle va contenir, un nombre, du texte, etc. On utilise en R les symboles accolés tiret et supérieur (ce qui ressemble un peu à une flèche) pour indiquer le contenu et la variable. Deux syntaxes sont possibles en R : variable <- calcul calcul -> variable La première forme avec d'abord le nom de la variable est la plus classique mais la seconde est la plus explicite et sans doute la plus compréhensible. La machine commence toujours par évaluer (calculer) la partie du coté du tiret de la flèche, ce qui explique que l'instruction variable <- variable + 1 a un sens qui signifie rajouter un à la variable, ce qui se dit incrémenter la variable. Lorsque la machine exécute "le code" (les instructions), elle procéde en séquence c'est-à-dire qu'elle exécute les instructions les unes à la suite des autres. C'est un peu un «jeu de piste» que de trouver ce que fait la machine lorsqu'on lit les instructions. Ainsi avec le code a <- 6 b <- 3 a <- a + b b <- a - b a <- a - b on trouve 3 dans la variable a et 6 dans la variable b, ce qui se nomme permuter les variables alors qu'avec le code a <- 6 b <- 3 a <- a - b b <- a + b a <- a - b on n'obtient rien de particulier (ou, plutôt, si,   on perd la valeur de a). Conclusion : il faut être très prudent(e), bien se relire, bien tout vérifier car on a vite fait de se tromper, surtout si on tape vite sur le clavier. Pour ceux et celles qui n'ont pas compris le détail de la permutation des variables, voici les explications écrites directement dans le code à l'aide de commentaires repérés par le symbole dièse (#). La machine ne tient pas compte du dièse et de ce qui le suit. Il est conseilé de mettre «suffisamment» de commentaires afin de pouvoir se relire et que les autres personnes qui lisent le code puissent le comprendre. a <- 6 # a contient 6 et b n'existe pas pour l'instant b <- 3 # a contient 6 et b contient 3 a <- a + b # a contient 9 et b contient 3 b <- a - b # a contient 9 et b contient 6 a <- a - b # a contient 3 et b contient 6 Il existe bien sûr des solutions plus simples, plus générales pour réaliser cette permutation. Le choix du nom des variables (en particulier le nombre de lettres de l'identifiant) et la façon de les écrire ne sont pas imposés, mais il existe plusieurs méthodes et surtout quelques conseils de bon sens. 2. Structures de données et affectations en R R est un langage vectoriel ce qui signifie que les vecteurs sont les éléments de base du langage. On peut créer des vecteurs de différentes façons, par exemple avec la fonction c(), la fonction seq(), la fonction vector(), la fonction rep() ou son raccourci : (le symbole deux-points)... Grâce à la fonction identical(), il est facile de vérifier que x et c(x) représentent le même objet. Le nombre d'éléments d'un vecteur se nomme sa longueur et s'obtient en R à l'aide de la fonction length(). x <- 2 y <- c(2) print( identical(x,y) ) # la machine répond TRUE (vrai, en anglais) a <- 2 b <- length(a) # b contient 1 c <- 5 d <- c(a,b,c) # le vecteur 2 1 5 print( length(d) ) # la machine répond 3 car il y a trois éléments dans d En R, a:b correspond aux vecteurs des entiers qui vont de a à b. Voici quelques exemples : 1:5 # le vecteur 1 2 3 4 5 2:0 # le vecteur 2 1 0 n <- 6 1:n+1 # le vecteur 2 3 4 5 6 7 (1:n)+1 # le vecteur 2 3 4 5 6 7 1:(n+1) # le vecteur 1 2 3 4 5 6 7 Comme le montrent les trois derniers exemples, R connait le calcul vectoriel : additionner 1 à un vecteur, c'est ajouter 1 à chacun des éléments du vecteur. De même, R sait additionner naturellement des vecteurs de même longueur, les multiplier... Il faut donc impérativement utiliser des parenthèses en cas de doute sur une opération ou réaliser une affectation supplémentaire pour obtenir un code lisible : # mettre les nombres de 1 à n+1 dans v (version 1) v <- 1:(n+1) # mettre les nombres de 1 à n+1 dans v (version 2) nn <- n+1 v <- 1:nn Maitriser la notation deux-points et les opérations vectorielles élémentaires est très important parce que cela permet d'effectuer de nombreux calculs et de générer de nombreuses valeurs à moindre frappe. En plus des vecteurs, R dispose des listes comme élements de base. Une liste nommée (nous ne conseillons pas d'utiliser des listes non nommées) se définit via le mot anglais list() -- on s'en serait douté ! On accède aux éléments d'une liste nommée via leur nom et le symbole $ (dollar). Le nombre d'éléments d'une liste se nomme sa longueur et s'obtient en R à l'aide de la fonction length() mais attention car une liste peut contenir plein de choses, des vecteurs, d'autres listes, etc. Voici quelques exemple qui se veulent explicites : a <- list(b=3,c=4) # a est une liste qui contient b et c print( a$b ) # la machine affiche la valeur 3 (contenu de b) length(a) # 2 car il y a deux éléments dans a names(a) # correspond aux noms dans a, soit le vecteur "b" "c" # une écriture pratique : res <- list(methode="simple", fichier="a35.xls", jour=28 ) # fin de list # on peut aussi commenter en partie droite xmp <- list(methode="simple", # ceci montre comment on fichier="a35.xls", # peut avoir du code très jour=28 # lisible pour une liste ) # fin de list # des listes plus générales : a <- 5 b <- list(a=a,c=8) c <- 1:3 d <- list(a,b,c,d=3) e <- list(x=1,y=c(2,3),z=list(a=4,b=5,c=6),t="bravo !") 3. Autres "objets" en R R dispose aussi de deux structures de données très importantes issues des vecteurs et des listes : ce sont les matrices et les data frames qui permettent de représenter respectivement des tableaux homogènes et hétérogènes classiques avec des lignes et des colonnes. Nous y reviendrons plus tard. Signalons aussi qu'il existe des tableaux généraux (array) mais dont on se passe la plupart du temps ! Pour connaitre la nature d'on objet, on peut utiliser la fonction class() : a <- 2 b <- c(1,5) c <- list(a,b) d <- "oui" class(a) # renvoie "numeric" class(b) # renvoie "numeric" aussi class(c) # renvoie "list" class(d) # renvoie "character" R a aussi des valeurs "spéciales" nommées NA, et NULL dont nous reparlerons plus tard, comme les résultats Inf, NAN et <NA>. Pour les plus impatient(e)s, le lien sous ces mots dans le tableau suivant mène à l'aide de R pour ces valeurs : mot signification  NA  Not Available  NULL  Rien (!)  NAN  Not a number (pas un nombre)  Inf  Infini 4. Affichage des variables en R On dispose de deux fonctions principales pour afficher les variables : la fonction print() et la fonction cat(). De plus on peut utiliser paste() et sprintf() pour respectivement concaténer des chaines ou les formater. Voici un petit pot-pourri qui montre la puissance de ces fonctions : > x <- 1 > cat(" x vaut ",x,"\n") x vaut 1 > n <- 10 > v <- 1:n > cat(" on dispose des ",n,"valeurs : ") on dispose des 10 valeurs : > print(v) 1 2 3 4 5 6 7 8 9 10 > cat(" on change \n de ligne \n") ; on change de ligne > w <- sprintf("%03d",v) > cat(" données formatées") données formatées > print(w) "001" "002" "003" "004" "005" "006" "007" "008" "009" "010" > x <- paste(w,collapse=" ; ") > print(x) "001 ; 002 ; 003 ; 004 ; 005 ; 006 ; 007 ; 008 ; 009 ; 010" > print(paste("serie",(1:5),".xls",sep="")) "serie1.xls" "serie2.xls" "serie3.xls" "serie4.xls" "serie5.xls" > cat(1:3,"\n") 1 2 3 > x <- list(a=1,b=2,c=3) > # attention : > cat(x) Erreur dans cat(list(...), file, sep, fill, labels, append) : argument 1 (type 'list') pas encore traité par cat > # une solution partielle > cat( paste(x,sep=" "), "\n") 1 2 3 > e <- list(x=1,y=c(2,3),z=list(a=4,b=5,c=6),t="bravo !") > cat(paste(e,sep=" "),"\n") 1 c(2, 3) list(a = 4, b = 5, c = 6) bravo ! 5. Spécificités du langage R R est un langage particulier puisqu'il est vectoriel. Du coup, on dispose facilement de séries de valeurs et de calculs idoines et en particulier on peut appliquer à des vecteurs des fonctions statistiques et mathématiques comme sum(), mean(), min, max... > # un vecteur > v <- c(1,8,2,7,4) > # exponentielle et logarithme des valeurs > print( exp(v) ) [1] 2.718282 2980.957987 7.389056 1096.633158 54.598150 > print( log(v) ) [1] 0.0000000 2.0794415 0.6931472 1.9459101 1.3862944 > # sprintf aussi est vectoriel : > print( sprintf("%6.1f", exp(v) ) ) [1] " 2.7" "2981.0" " 7.4" "1096.6" " 54.6" > # sa moyenne et sa médiane > print( c(mean(v),median(v)) ) [1] 4.4 4.0 > # le min et le max > print( c(min(v),max(v)) ) [1] 1 8 > # la fonction range : > print( range(v) ) [1] 1 8 De façon subtile, R distingue les entiers des réels. Ainsi 1 est un réel alors que 1L est un entier. Comme : renvoie des entiers, il est normal que 1:2 ne soit pas égal à c(1,2) mais bien à c(1L,2L). Il faut aussi noter que les vecteurs sont toujours "plats", homogènes en type et que R convertit sans prévenir. Cela peut avoir de graves conséquences : > # un vecteur d'entier > x <- c(1L,8L) > cat(" nature : ",class(x)," somme (1) :",sum(x) ) nature : integer somme (1) : 9 > # on ajoute un réel > x <- c(x,2) > cat(" nature : ",class(x)," somme (2) :",sum(x) ) nature : numeric somme (2) : 11 > # un vecteur est toujours "plat" > x <- c( x, c(x,2) , 2 ) > cat(" nature : ",class(x)," somme (2) :",sum(x) ) nature : numeric somme (2) : 26 > # on ajoute une chaine de caractères > x <- c(x,"oui") > cat(" nature : ",class(x)," somme (3) :",sum(x) ) Erreur dans sum(x) : 'type' (character) de l'argument incorrect Signalons au passage que les fonctions sont des variables et qu'on peut donc les inclure dans des listes... a <- 1L b <- 2 c <- "oui" d <- sum e <- list(a=a,b=b,c=c,d=d) Enfin, il faut noter que l'affectation est aussi une fonction. La notation <- n'est qu'un raccourci d'écriture : # en R, l'affectation est une fonction "<-"(x,1) # équivalent à x <- 1 # une autre écriture : assign("x",1)   Partie 3 - Conditions logiques et tests   Table des matières cliquable   1. Valeurs logiques et tests en R   2. Filtrage vectoriel   3. Applications aux matrices et dataframes   4. Spécificités du langage R 1. Valeurs logiques et tests en R R dispose de deux valeurs logiques nommées FALSE et TRUE qui valent numériquement 0 et 1. Les opérateurs qui renvoient des valeurs logiques sont très classiquement < et >. Il faut leur adjoindre <= et >= et aussi == (bien noter qu'il y a deux signes "égal") pour tester l'égalité. Pour des variables simples, les connecteurs usuels nommés NON, ET, OU s'écrivent respectivement !, &, |. Il est très fortement conseillé d'utiliser des parenthèses pour séparer ces comparaisons logiques. Voici quelques exemples d'utilisation : x <- 5 x==2 # FALSE x==5 # TRUE !(x>4) # FALSE x<2 # FALSE x>=5 # TRUE x>3 # TRUE (x>3) & (x<10) # TRUE (x>0) | (x==2) # TRUE TRUE + 1 # 2 FALSE*FALSE # 0 !7 # FALSE Pour réaliser un test logique, on utilise une structure algorithmique dite d'alternative qui, en fonction d'une condition (opération à résultat logique), effectue une bloc d'instructions. Voici les deux formes algorithmiques, nommées respectivement SI_ALORS et SI_ALORS_SINON : ############################################## # # # structure "si_alors" # # # ############################################## SI (condition) ALORS [...] # bloc d'instructions exécutées # si la condition est vraie FINSI ############################################## # # # structure "si_alors_sinon" # # # ############################################## SI (condition) ALORS [...] # bloc d'instructions exécutées # si la condition est vraie SINON [...] # bloc d'instructions exécutées # si la condition est fausse FINSI La traduction en R se fait à l'aide des mots if, else et des accolades { et } pour délimiter les blocs d'instruction. De telles structures permettent donc de modifier l'exécution en séquence des instructions. ############################################## # # # structure "si_alors" en R # # # ############################################## if (condition) { [...] # bloc d'instructions exécutées # si la condition est vraie } ############################################## # # # structure "si_alors_sinon" en R # # # ############################################## if (condition) { [...] # bloc d'instructions exécutées # si la condition est vraie } else { [...] # bloc d'instructions exécutées # si la condition est fausse } Voici deux exemples en R. On remarquera que nous avons (ce qui est très fortement conseillé) commenté les fins de SI. # STRUCTURE si Exemple 1 # ---------------------- # on indique quand on a commencé à traiter le fichier numéro 100 # (nbf est le numéro de fichier en cours de traitement) if (nbf==100) { cat(" fichier numéro ",nbf," atteint. \n") cat(" date et heure : ",date(),"\n\n") } # fin si nbf=100 # STRUCTURE si Exemple 2 # ---------------------- if (valCour>maxLoc) { # on met à jour le maximum local via la valeur courante maxLoc <- valCour nbInf <- 0 } else { nbInf <- nbInf + 1 } # fin si L'instruction stop en R permet de quitter le script en cours. Cela peut se révéler utile, par exemple si le fichier que l'on veut traiter n'est pas trouvé (noter le mot si dans cette phrase). Voici comment s'en servir : ## série de calculs sur un fichier nommé FN if (!file.exists(FN)) { cat("ATTENTION ! Le fichier ",FN," n'est pas présent.\n\n") ; stop(" donc arrêt du programme.\n") ; } # fin de si # si on arrive ici, c'est que le fichier existe ## suite des calculs... La valeur NA de R qui signifie Not Available, soit Non Accessible en français est aussi une valeur logique ce qui complique les cas à tester : # NA est aussi une valeur logique x <- NA print(class(x)) # renvoie "logical" # un test raté avec x : # R répond # Error in if (x < 0) { : # valeur manquante là où TRUE / FALSE est requis if (x<=0) { cat(" x est négatif ou nul\n") } else { cat(" x n'est pas négatif ou nul...\n") cat(" mais il n'est peut-être pas positif") cat(" ni même numérique.\n") } # fin si # un test réussi avec x # R répond x est indéterminé (NA). if (is.na(x)) { cat(" x est indéterminé (NA).\n") } else { if (x<0) { cat(" x est strictement négatif\n") } else { cat(" x est positif ou nul.\n") } # fin si x<0 } # fin si is.na(x) 2. Filtrage vectoriel R est beaucoup plus puissant avec les tests logiques qu'on ne l'imagine car on peut coupler l'indexation avec ces tests et donc réaliser des affectations conditionnelles. Pour accéder à un élément dans un vecteur, R fournit la notation "crochets" : ainsi x[k] correspond à l'élément numéro k sachant que, contrairement à la plupart des autres langages de programmation, R commence la numérotation à 1. Donc x[0] -- qui existe par ailleurs en R -- ne correspond pas au premier élément de x. La notation crochets ou indexation permet de spécifier plusieurs éléments. Ainsi [1:n] correspond aux n premiers éléments. Un indice entier mais négatif signifie tout sauf cet indice donc (1:5)[ - c(3,4) ] renvoie 1 2 5. Lorsqu'on fournit entre crochets pour une variable de type vecteur un vecteur de même longueur que cette variable composé de 0 et de 1, R extrait les valeurs correspondant à 1. Par exemple (1:3)[ c(0,1,0) ] renvoie 2. Comme nous avons expliqué que les valeurs logiques FALSE et TRUE valent numériquement 0 et 1, il est facile de comprendre que R fournit un mécanisme de filtrage très puissant avec les expressions logiques vectorielles. Voici des exemples : # le vecteur v # pos 1 2 3 4 5 6 7 8 9 v <- c( 1, 8, 2, -5, 15, 6, 9, -1, 4) # filtre des négatifs # pos 1 2 3 4 5 6 7 8 9 v<0 # renvoie FALSE FALSE FALSE TRUE FALSE FALSE FALSE TRUE FALSE # num 0 0 0 1 0 0 0 1 0 # extraction des négatifs v[ v<0 ] # renvoie -5 -1 # comptage du nombre de positifs sum( v>0 ) # renvoie 7 # les éléments de v entre 3 et 10 flt1 <- (v>3) flt2 <- (v<10) v[ flt1 & flt2 ] # renvoie 8 6 9 4 3. Applications aux matrices et dataframes En plus des vecteurs, R dispose de deux structures de données nommées matrix et data frame qui définissent des tableaux rectangulaires avec des lignes et des colonnes. Il y a toutefois des grandes différences entre ces deux structures. Les matrices sont homogènes en type et les lignes et les colonnes y sont équivalentes en fonctionnement alors que les data frames sont des listes particulières : les éléments de la liste sont les colonnes du tableau, avec la contrainte que toutes les colonnes doivent avoir le même nombre d'éléments. Un data frame est donc particulièrement adapté à contenir un fichier de données pour des études statistiques, avec des colonnes de types éventuellement différents. Toutes les fonctions de R qui lisent des fichiers comme la fonction read.table(), la fonction read.xls() (du package gdata) renvoient des data frames. Les conditions logiques et le filtrage vectoriel permettent d'extraire facilement des sous-ensembles de ces tableaux de données comme le montrent les exemples ci-dessous pour le fichier de données elf.txt : # lecture du fichier elf.txt # elf <- read.table("http://forge.info.univ-angers.fr/~gh/wstat/Programmation_R/Programmation_introduction/elf.txt",head=TRUE) # extrait des données > head(elf) NUM SEXE AGE PROF ETUD REGI USAG 1 M001 1 62 1 2 2 3 2 M002 0 60 9 3 4 1 3 M003 1 31 9 4 4 1 4 M004 1 27 8 4 1 1 5 M005 0 22 8 4 1 2 6 M006 1 70 4 1 1 1 > tail(elf) NUM SEXE AGE PROF ETUD REGI USAG 94 M094 0 12 12 2 1 0 95 M095 1 31 6 4 0 0 96 M096 1 17 12 3 1 0 97 M097 1 39 1 2 1 0 98 M098 0 62 6 3 1 0 99 M100 1 48 9 4 2 0 # filtre "femme" flt1 <- elf$SEXE==1 # filtre "jeune" flt2 <- elf$AGE <20 # nombre de femmes sum( flt1 ) # nombre de jeunes sum( flt2 ) # nombre de femmes jeunes sum( flt1 & flt2 ) # extraction du tableau des femmes jeunes fj1 <- elf[ (flt1 & flt2) , ] # autre solution fj2 <- subset(elf, flt1 & flt2) # attention à ne pas écrire fj3 <- subset(elf, SEXE=1, AGE<20) 4. Spécificités du langage R En R, les indices commencent à 1. C'est une révolution par rapport aux autres langages de programmation qui ne comptent pas en position mais en décalage (offset) à partir du début du tableau. Cela facilite beaucoup les calculs. A cause de la valeur NA -- qui est spécifique à R, la comparaison entre valeurs en R est compliquée : ## un vecteur x logique x <- c( NA, FALSE, TRUE ) ## table AND obtenue par outer(x, x, "&") <NA> FALSE TRUE <NA> NA FALSE NA FALSE FALSE FALSE FALSE TRUE NA FALSE TRUE ## table OR obtenue par outer(x, x, "|") <NA> FALSE TRUE <NA> NA NA TRUE FALSE NA FALSE TRUE TRUE TRUE TRUE TRUE Heureusement il y a de nombreuses fonctions comme is.na() et na.omit() qui permettent de détecter et d'enlever ces valeurs NA. On trouve aussi, comme pour la fonction sum(), une option na.rm=TRUE qui enlève (localement) ces valeurs NA. R dispose de nombreuses fonctions logiques : > apropos("^is.") [1] "is.array" "is.atomic" "isatty" "isBaseNamespace" "is.call" "is.character" "isClass" [8] "isClassDef" "isClassUnion" "is.complex" "is.data.frame" "isdebugged" "is.double" "is.element" [15] "is.empty.model" "is.environment" "is.expression" "is.factor" "is.finite" "is.function" "isGeneric" [22] "isGrammarSymbol" "isGroup" "isIncomplete" "is.infinite" "is.integer" "islands" "is.language" [29] "is.leaf" "is.list" "is.loaded" "is.logical" "is.matrix" "is.mts" "is.na" [36] "is.na<-" "is.na.data.frame" "is.na<-.default" "is.na<-.factor" "is.name" "isNamespace" "is.nan" [43] "is.na.numeric_version" "is.na.POSIXlt" "is.null" "is.numeric" "is.numeric.Date" "is.numeric.difftime" "is.numeric.POSIXt" [50] "is.numeric_version" "is.object" "ISOdate" "ISOdatetime" "isOpen" "is.ordered" "isoreg" [57] "is.package_version" "is.pairlist" "is.primitive" "is.qr" "is.R" "is.raster" "is.raw" [64] "is.recursive" "is.relistable" "isRestart" "isS4" "isSealedClass" "isSealedMethod" "isSeekable" [71] "is.single" "is.stepfun" "is.symbol" "isSymmetric" "isSymmetric.matrix" "is.table" "isTRUE" [78] "is.ts" "is.tskernel" "is.unsorted" "is.vector" "isVirtualClass" "isXS3Class" Comme nous l'avons dit précédemment, les structures de données de base sont les vecteurs et les listes. Il faut néanmoins bien connaitre les data frames et les matrices (et leurs "pièges") pour écrire de "beaux" programmes concis : # quelques pièges des data frames # ------------------------------- > v1 <- 1:2 # nos données > v2 <- c("oui","non") # class(v2) renvoie "character" > d <- data.frame(v1,v2) # attention, voici le data frame > class(d) # sa classe [1] "data.frame" > is.list(d) # est-ce une liste ? [1] TRUE # oui ! > is.data.frame(d) # est-ce aussi un data frame ? [1] TRUE # oui, bien sûr > is.vector(d$v1) # quelle classe pour d$v1 ? [1] TRUE # facile > is.vector(d$v2) # et pour d$v2 ? [1] FALSE # perdu, data.frame() convertit en facteur par défaut > d$v1 # la preuve : [1] 1 2 > d$v2 [1] oui non Levels: non oui > is.factor(d$v2) # vérfication [1] TRUE # quelques pièges des matrices # ------------------------------- > m <- matrix(c(v1,v1*2,v1**2),nrow=3) > is.matrix(m) # facile [1] TRUE > is.vector((m[,2])) # aussi simple [1] TRUE > is.integer((m[,2])) # plus difficile [1] FALSE # car 1 et 2 sont des réels (ce n'est pas 1L et 2L) > m[1,2] <- "0" > is.factor((m[,2])) # pas de transformation en facteur [1] FALSE > is.character((m[,2])) # mais conversion de TOUTE la matrice en caractères [1] TRUE Il faut noter que R permet d'affecter des parties de vecteur grâce à l'indexation et au filtrage logique. Ainsi l'instruction : v[ (v<5) ] <- 0 vient remplacer dans v toutes les valeurs strictements inférieures à 5 par 0. Enfin, il existe sous R plusieurs fonctions qui évitent de faire des tests logiques pour trouver des valeurs, les remplacer... comme les fonctions ifelse(), which(), grep(), sub()...   Partie 4 - Boucles et itérations   Table des matières cliquable   1. Boucles "TANT QUE"   2. Boucles "POUR"   3. Boucles "REPETER JUSQU'A"   4. Itérations et sorties de boucles   5. Imbrications, itérations et sorties de boucles   6. Exemples de boucles usuelles (mais potentiellement lentes) en R   7. Comment et pourquoi éviter les boucles pour en R   8. Spécificités du langage R 1. Boucles "TANT QUE" La boucle TANT QUE (while en anglais) est un peu comme une structure si répétitive. Sa syntaxe algorithmique est la suivante : # structure algorithmique TANT QUE # -------------------------------- TANT QUE (condition) [...] # bloc d'instructions exécutées # tant que la condition reste vraie FINTANT QUE Son écriture en R est immédiate : # traduction en R de la boucle TANT QUE # ------------------------------------- while (condition) { # bloc d'instructions } En voici un exemple : # exemple de boucle TANT QUE : # recherche du premier symbole point dans un nom de fichier # ------------------------------------------------------------------- nomFic <- "essai.serie1.xls" posPoint <- 0 while (substr(nomFic,posPoint,posPoint)!=".") { posPoint <- posPoint + 1 } # fin tant que cat(" le point est vu en position ",posPoint,"dans le fichier ",nomFic,"\n") Il faut être très prudent(e) avec une boucle tant que car l'ordinateur peut boucler pendant un temps infini si la condition est mal écrite. Ainsi dans l'exemple précédent, nous avons malheureusement oublié que la machine ne doit pas aller après le dernier caractère. Supposer qu'un nom de fichier contient toujours un point serait une erreur de conception et le code précédent ne s'arrête jamais s'il n'y a pas de point dans le nom de fichier. Voici ce qu'il faut écrire pour avoir un code correct : # recherche du premier symbole point dans un nom de fichier # avec une boucle TANT QUE qui se termine forcément nomFic <- "essai.serie1.xls" posPoint <- 0 nbcar <- nchar(nomFic) while ( (substr(nomFic,posPoint,posPoint)!=".") & (posPoint<nbcar)) { posPoint <- posPoint + 1 } # fin tant que if (posPoint>nbcar) { cat(" le point n'est pas dans le nom du fichier\n") } else { cat(" le point est vu en position ",posPoint,"dans le fichier ",nomFic,"\n") } # fin si # remarque : une "vraie" solution R serait, sans boucle tant que : # # posPoint <- which(strsplit(nomFic,split="")[[1]]==".") # # et which(unlist(strsplit(nomFic,split=""))==".") # # pour trouver toutes les positions du point dans nomFic 2. Boucles "POUR" Lorsque le nombre de répétitions est connu, que ce soit une valeur constante comme 10 ou le nombre des éléments d'un vecteur, on peut utiliser une autre structure répétitive, nommée boucle POUR dont voici la syntaxe algorithmique : # structure algorithmique POUR # ---------------------------- POUR indice DE valeurInitiale A valeurFinale # bloc d'instructions exécutées # avec la valeur indice FINPOUR Là encore, son écriture en R est immédiate : # traduction en R de la boucle POUR # --------------------------------- for (indice in (valeurInitiale : valeurFinale) ) { # bloc d'instructions } Et un exemple peut être : # exemple : correspondance entre lettres et chiffres # ------------------------------------------------------------------- for (indLet in (1:5) ) { lettre <- LETTERS[ indLet] cat("la lettre",lettre,"est en position",indLet,"\n") } ; # fin pour indLet # affichage : ------------- la lettre A est en position 1 la lettre B est en position 2 la lettre C est en position 3 la lettre D est en position 4 la lettre E est en position 5 Dans les faits, R dispose d'une boucle POUR plus générale d'itération nommée aussi for. Voici des exemples : # boucle POUR générale en R # ---------------------------- for (ELEMENT in STRUCTURE) { # bloc d'instructions } ## boucles POUR sur les colonnes d'un dataframe # via les noms de colonne for (nom in names(df) ) { [...] } # fin pour nom # via les numéros de colonne pdvCol <- 1:ncol(df) # plage de variation for (indcol in pdvCol) { } # fin pour indcol 3. Boucles "REPETER JUSQU'A" Le troisième type de boucle disponible consiste à faire le test pour savoir si on recommence la boucle en fin de corps de boucle. La syntaxe algorithmique est la suivante : # structure algorithmique REPETER # -------------------------------- REPETER [...] # bloc d'instructions exécutées JUSQU'A (condition) Sa traduction n'est pas immédiate en R parce qu'on écrit seulement repeat { # bloc d'instructions exécutées } Il faut impérativement passer par break ou stop() pour sortir de la boucle REPETER JUSQU'A en R. Voici un exemple d'une telle boucle en R qui demande un nom de fichier et teste si le fichier est présent avant d'aller plus loin : repeat { nomf <- readline(" donner le nom d'un fichier : ") if (!file.exists(nomf)) { cat(" fichier",nomf," nom vu dans le répertoire courant.\n") } else { break } # fin de si } # fin de répéter cat(" ok, traitement du fichier ",nomf,"\n") Attention : il y beaucoup de fonctions R qui dispensent d'écrire des boucles. Il est prudent de les apprendre parce que l'exécution des boucles en R est souvent lente à cause de la gestion en mémoire des variables. Ainsi la fonction cbind() fournit nativement la correspondance entre indice et élément. 4. Itérations et sorties de boucles Il peut arriver que l'on veuille sortir d'une boucle ou du script. Quelque soit le type de boucle, la fonction stop() quitte le script en cours alors que l'instruction break permet de sortir de la boucle. On peut aussi utiliser next pour forcer la machine à passer à l'itération suivante. Voici des exemples : # une boucle infinie d'interpréteur repeat { cat("Donner un entier dont vous voulez le carré ou 0 pour arrêter : ") rep <- as.numeric(readline()) if (rep==0) { break } cat(" le carre de ",rep," est ",rep**2,"\n") } # fin répéter_jusqu'à L'exécution de cette boucle aboutit aux résultats suivants : Donner un entier dont vous voulez le carré ou 0 pour arrêter : 5 le carre de 5 est 25 Donner un entier dont vous voulez le carré ou 0 pour arrêter : 8 le carre de 8 est 64 Donner un entier dont vous voulez le carré ou 0 pour arrêter : 0 5. Imbrications, itérations et sorties de boucles Comme pour les tests, on peut imbriquer les boucles, éventuellement de différents types. De plus, un corps de boucle contient des instructions, donc on peut avoir une boucle à l'intérieur de la partie "sinon" d'un test, qui contient elle-même un autre test avec une autre boucle, etc. On veillera à ne pas trop multiplier l'imbrication des structures de façon à pouvoir s'y retrouver facilement. Trois ou quatre niveaux d'imbrication (une boucle dans un test dans une boucle dans...) parait être la limite supportable de la compréhension. Au-delà, il faut certainement recourir à un sous-programme (une fonction) pour que ce soit lisible... Voici des exemples avec chacun des types de boucles qui illustrent ces points. Nous commençons avec deux boucles POUR imbriquées pour afficher les valeurs de x^y inférieures à 1 million pour les nombres x et y de 1 à 10. On affiche les puissances de 1, de 2, de 3... ligne par ligne. Pour éviter de calculer mathématiquement jusqu'à quel terme on doit aller, on calcule la puissance et on ne l'affiche que si elle est inférieure à un million. Voici le code R correspondant : # boucles imbriquées et BREAK cat("table des puissances inférieures ou égales à 1 million\n") for (indi in 1:10) { for (indj in 1:10) { puiss <- indi**indj if (puiss<=10**6) { cat(sprintf("%9d",puiss)) } else { break } # fin si } # fin pour indj cat("\n") } # fin pour indi et le résultat de son exécution table des puissances inférieures ou égales à 1 million 1 1 1 1 1 1 1 1 1 1 2 4 8 16 32 64 128 256 512 1024 3 9 27 81 243 729 2187 6561 19683 59049 4 16 64 256 1024 4096 16384 65536 262144 5 25 125 625 3125 15625 78125 390625 6 36 216 1296 7776 46656 279936 7 49 343 2401 16807 117649 823543 8 64 512 4096 32768 262144 9 81 729 6561 59049 531441 10 100 1000 10000 100000 1000000 Le deuxième exemple montre comment tester une fonction à l'aide d'une réponse utilisateur via une boucle REPETER . Ici, nous avons pris l'exemple de la fonction qui calcule le carré pour des raisons de simplicité. L'idée est ici de demander une valeur à l'utilisateur, d'afficher le résultat de la fonction et de recommencer. Nous avons décidé arbitrairement qu'entrer la valeur zéro fait sortir de la boucle. # une boucle infinie d'interpréteur repeat { cat("Donner un entier dont vous voulez le carré ou 0 pour arrêter : ") rep <- as.numeric(readline()) if (rep==0) { break } cat(" le carre de ",rep," est ",rep**2,"\n") } # fin répéter_jusqu'à L'exécution de cette boucle aboutit aux résultats suivants, sachant que l'utilisateur a saisi 5, puis 8 puis 0 (afin d'arrêter le calcul). Donner un entier dont vous voulez le carré ou 0 pour arrêter : 5 le carre de 5 est 25 Donner un entier dont vous voulez le carré ou 0 pour arrêter : 8 le carre de 8 est 64 Donner un entier dont vous voulez le carré ou 0 pour arrêter : 0 Comme troisième exemple, nous essayons de traiter avec une boucle TANT QUE. tous les fichiers-texte du répertoire avec une numérotation régulière lorsqu'ils ont plus de deux lignes : numFic <- 1 nomFic <- paste("fic",sprintf("%03d",numFic),".txt",sep="") while (file.exists(nomFic)) { lignes <- readLines(nomFic) nbLign <- length(lignes) cat(" le fichier ",nomFic," comporte ",nbLign," lignes\n") if (nbLign<2) { stop("-- fin de parcours des fichiers.\n") } # fin si numFic <- numFic + 1 nomFic <- paste("fic",sprintf("%03d",numFic),".txt",sep="") } # fin tant que cat("tous les fichiers ont été traités.\n") Un exemple d'éxécution, avec quelques fichiers présents dans notre répertoire courant fournit l'affichage suivant. On remarquera que R écrit Erreur lorsqu'on fait appel à la fonction stop() . le fichier fic001.txt comporte 3 lignes le fichier fic002.txt comporte 2 lignes le fichier fic003.txt comporte 3 lignes le fichier fic004.txt comporte 1 lignes Erreur : -- fin de parcours des fichiers. 6. Exemples de boucles usuelles (mais potentiellement lentes) en R Nous présentons ici quelques boucles faussement susceptibles d'être utiles. En effet, la plupart de ces boucles explicites peuvent être remplacées à moindre coût d'écriture par des fonctions de R prévues pour cela. Ces exemples ne sont donc fournis qu'à titre d'entrainement à la lecture de boucles et ne sont pas optimisés. Nous aurons l'occasion de revoir un peu plus tard comment réaliser les traitements associés à ces boucles de façon beaucoup plus "propre et concise" et, en tous cas, dans l'esprit de R. 6.1 Traitement de toutes les colonnes d'un data frame Il arrive assez fréquemment qu'on ait à traiter toutes les colonnes numériques quantitatives d'un data frame, par exemple pour en calculer systématiquement les moyennes, les médianes (au fait, vous vous souvenez de la différence statistique entre ces deux indicateurs de tendance centrale et pourquoi on calcule la moyenne des tailles, la médiane des poids pour les humains et pas l'inverse ?)... R fournit avec la fonction ncol() le nombre de colonnes d'un data frame et avec la fonction names() le nom de ces colonnes. Il pourrait être tentant d'écrire une boucle comme for (indCol in 1:ncol(df)) { nomCol <- names(df)[indCol] cat("traitement de la colonne numéro",indCol,"soit",nomCol,"\n") } # fin pour indCol mais c'est certainement se fatiguer beaucoup, surtout si le numéro de colonne n'est pas utilisé. Il est possible en R de passer directement en revue les noms de colonne. Au passage, nous montrons comment construire un fichier graphique de type .png dont le nom reprend celui de la colonne en cours, après détection du type numérique de la colonne : for (col in names(df)) { # pour chaque nom de colonne if (is.numeric(col)) { # s'il s'agit de données numériques ficPng <- paste(col,".png",sep="") # suite du traitement de la colonne } # fin si } # fin pour col 6.2 Calculs par sous-groupe Imaginons maintenant que nous voulions parcourir toutes les lignes d'un data frame pour compter (maladroitement) via le code-sexe (variable SX) le nombre d'hommes (SX=1) et de femmes (SX=2). De façon encore plus maladroite, nous allons mettre dans la variable agesH les ages des hommes et dans la variable agesF les ages des femmes. Voici ce qu'il ne faut pas faire, mais au moins, vous l'aurez vu et vous saurez l'éviter : # exemple de calcul par sous-groupe # (non optimisé) nbInd <- nrow(df) nbHom <- 0 # comptage du nombre d'hommes nbFem <- 0 # mais alors "où sont les femmes ?", comme dit Patrick Juvet agesH <- c() # ages des hommes agesF <- c() # ages des femmes for (indLig in (1:nbInd)) { if (df[indLig,"SX"]==1) { nbHom <- nbHom + 1 agesH <- c(ageH,df[indLig,"AGE"]) } else { nbFem <- nbFem + 1 agesF <- c(ageF,df[indLig,"AGE"]) } # finsi } # fin pour indLing 6.3 Traitement d'une liste de fichiers et moyenne dans un tableau On veut traiter n fichiers, disons ficSerie01.txt, ficSerie02.txt, ficSerie03.txt... mais ce pourrait être bien sûr des fichiers Excel. Une fois le traitement de chaque fichier effectué, on veut obtenir un tableau et un fichier .CSV résumé des traitements. Pour notre exemple, nous allons limiter le traitement, via la fonction traiteFichier() à la détermination du nombre de lignes du fichier. Voici cette fonction : # exemple de traitement d'un fichier # réduit à la détermination de son nombre de lignes traiteFichier <- function( nomFic ) { if (!file.exists(nomFic)) { cat("fichier",nomFic,"non vu.\n") } else { dataFic <- read.table(nomFic,head=TRUE) nbl <- nrow(dataFic) cat("il y a",nbl,"lignes de données dans",nomFic,"\n") } # fin si } # fin de fonction traiteFichier Une fois la fonction traiteFichier() mise au point, on peut écrire -- même si ce n'est pas la seule et la meilleure solution -- une boucle pour passer en revue une série de fichiers : # traitement d'une série de fichiers # à l'aide de la fonction traiteFichier() # désignation des fichiers (plusieurs exemples) nomsFichiers <- c("fichier1.txt","ficDeux.txt","fic_serie3.xtxt") nbfic <- 3 nomsFichiers <- paste("ficSerie",sprintf("%02d",1:nbfic),".txt",sep="") for (nomfic in nomsFichiers) { traiteFichier( nomfic ) } # fin pour nomfic Afin d'obtenir un tableau résumé, il faut prévoir un data.frame pour accueillir les résultats et modifier la fonction traiteFichier() pour qu'elle renvoie un résultat par fichier. On remplit alors au fur et à mesure la structure d'accueil dans la boucle. Une fois la boucle terminée, on peut afficher les résultats et les sauvegarder. Voici la fonction modifiée : # exemple de traitement d'un fichier # réduit à la détermination de son nombre de lignes # on renvoie ce nombre de lignes # ou NA si le fichier n'est pas vu traiteFichier <- function( nomFic ) { cats(paste("Traitement du fichier",nomFic)) if (!file.exists(nomFic)) { cat("fichier",nomFic,"non vu.\n") nbl <- NA } else { dataFic <- read.table(nomFic,head=TRUE) nbl <- nrow(dataFic) cat("il y a",nbl,"lignes de données dans",nomFic,"\n") } # fin si return(nbl) } # fin de fonction traiteFichier Le script qui comporte la boucle et la gestion du data.frame est le suivant : # traitement d'une série de fichiers # à l'aide de la fonction traiteFichier() # on sauvegarde dans un tableau l'information # renvoyée (le nombre de lignes), on l'affiche # et on l'exporte dans un fichier .CSV # désignation des fichiers nbfic <- 3 nomsFichiers <- paste("ficSerie",sprintf("%02d",1:nbfic),".txt",sep="") # structure d'accueil des résultats (data frame) tabRes <- data.frame(matrix(NA,nrow=nbfic+1,ncol=2)) names(tabRes) <- c("fichier","nombre de lignes") # boucle de traitement et remplissage de la structure d'accueil idf <- 0 # numéro courant de fichier for (nomfic in nomsFichiers) { idf <- idf + 1 nblc <- traiteFichier( nomfic ) tabRes[ idf, 1 ] <- nomfic tabRes[ idf, 2 ] <- nblc } # fin pour nomfic cats("Analyse globale des fichiers") # ajout de la moyenne sur l'ensemble des fichiers tabRes[ (nbfic+1), 1 ] <- "moyenne" tabRes[ (nbfic+1), 2 ] <- mean(as.numeric(tabRes[(1:nbfic),2])) # affichage et export cat("Voici le tableau résumé\n") print(tabRes) nomCsv <- "nblRes.csv" write.csv(x=tabRes,file=nomCsv) cat("\nrésultats écrits dans",nomCsv,"\n") Exemple d'exécution avec les fichiers cités : Traitement du fichier ficSerie01.txt ==================================== il y a 100 lignes de données dans ficSerie01.txt Traitement du fichier ficSerie02.txt ==================================== il y a 30 lignes de données dans ficSerie02.txt Traitement du fichier ficSerie03.txt ==================================== il y a 40 lignes de données dans ficSerie03.txt Analyse globale des fichiers ============================ Voici le tableau résumé fichier nombre delignes 1 ficSerie01.txt 100.00000 2 ficSerie02.txt 30.00000 3 ficSerie03.txt 40.00000 4 moyenne 56.66667 résultats écrits dans nblRes.csv Fichier CSV produit : "","fichier","nombre delignes" "1","ficSerie01.txt",100 "2","ficSerie02.txt",30 "3","ficSerie03.txt",40 "4","moyenne",56.6666666666667 7. Comment et pourquoi éviter les boucles pour en R Les boucles, et en particulier les boucles POUR, sont souvent le moyen de réaliser des calculs par itération dans les langages de programmation "classiques". CE N'EST PAS LE CAS EN R parce que R est un langage vectoriel. De nombreuses fonctions s'appliquent directement aux vecteurs, comme sum() ; pour les matrices et les listes, il faut utiliser des fonctions comme apply(), lapply(), sapply() et tapply()... Et il y a beaucoup d'autres fonctions prévues pour couvrir de nombreux autres cas, comme table(), split(), sweep()... Nous verrons à la séance 6 comment on arrive à se passer des boucles et à la séance 8 comment optimiser des boucles si on doit vraiment les utiliser. 8. Spécificités du langage R Une programmeuse, un programmeur C ou Java "classique" a l'habitude des boucles POUR dès qu'il s'agit de parcourir une structure. En R , il y a beaucoup d'autres solutions et il faut du temps pour les connaitre. Ainsi, et même si ce n'est pas "la" bonne solution, pour obtenir la variable précédente agesH qui contient les ages de hommes, on peut se contenter en R d'utiliser le filtrage vectoriel et écrire agesH <- df$AGE[ df$SX==1 ] ou, de façon plus lisible : agesH <- with(df, AGE[ SX==1 ] ) Il est clair qu'on est loin de l'écriture d'une boucle explicite. Même lorsqu'on veut utiliser des boucles POUR en R il faut se méfier. Ainsi l'expression for (i in 1:length(V)) n'est pas une "bonne" écriture. En effet, si le vecteur V est vide, sa longueur est nulle. Dans un langage classique, une boucle de 1 à 0 n'est pas exécutée. Pour R, la notation 1:0 signifie qu'on veut aller de 1 à 0 et il exécutera la boucle ! Ce qui est pire, c'est que V[i] ne renverra pas alors forcément d'erreur lorsque i vaut 0. Il est donc conseillé d'utiliser for (i in seq_along(V)) pour parcourir les indices de V car si V est vide, R ne rentrera pas dans la boucle avec cette écriture.   Partie 5 - Sous-programmes : les fonctions   Table des matières cliquable   1. Définition des fonctions nommées et anonymes   2. Définition et utilisation des paramètres   3. Tests des paramètres   4. L'ellipse notée ...   5. Quelques exemples de fonctions   6. Spécificités du langage R 1. Définition des fonctions nommées et anonymes Pour définir une fonction nommée, il faut réaliser une affectation avec comme partie gauche le nom de la fonction à créer, puis utiliser le mot function, mettre des parenthèses, ajouter des paramètres s'il y en a besoin avec éventuellement des valeurs par défaut, puis écrire le corps de la fonction entre accolades et mettre return avec des parenthèses pour indiquer l'objet renvoyé, qui peut être une simple valeur ou quelque chose de plus complexe. Par exemple, pour inventer une fonction qui calcule le carré d'une valeur, on devrait écrire carre <- function(x) { return(x*x) }            Il est possible de raccourcir le corps de la fonction en omettant les accolades et en mettant comme dernière (ou comme seule) instruction le calcul à renvoyer. Ainsi, on pourrait écrire carre <- function(x) x*x            Une écriture aussi concise est utile dans le cas d'une fonction intégrée à un appel de fonction ou pour une fonction anonyme (concept détaillé un peu plus bas dans cette section), mais cette écriture est dangereuse et «fainéante». Il vaut mieux lui préférer le code suivant : carre <- function(x) {            # calcule le carré de son argument            y <- x*x      return(y)            } # fin de fonction carre            Nous reviendrons sur ces écritures, mais un grand principe de la programmation robuste est qu'il faut préférer la lisibilité, la facilité de relecture et la maintenance du code à la facilité d'écriture. Il faut viser l'écriture de programmes robustes et lisibles et non pas de programmes vite tapés sur le clavier. Pour se servir de cette fonction carre() il suffit de l'appeler là où on utiliserait le carré des valeurs. Cela peut donc être dans le cadre d'un calcul simple ou d'un affichage interactif (en console), dans le cadre d'une instruction d'affectation etc. Il n'est pas obligatoire ici de nommer le paramètre au niveau de l'appel, mais il vaudra mieux le faire quand il y en aura plus d'un. On peut aussi utiliser juste le nom de la fonction en tant que paramètre quand cela est permis. Le calcul effectué par notre fonction étant "vectoriel", c'est-à-dire applicable à une structure, notre fonction est elle-même vectorielle. Voici des exemples d'utilisation : ## définition de la fonction            carre <- function(x) {            # calcule le carré de son argument            y <- x*x            return(y)            } # fin de fonction carre            # ------------------------------------------------------            # calcul interactif            carre(5) # suffisant, mais carre(x=5) est OK aussi            # affichage en interactif            cat("le carré de 8 est ",sprintf("%05d",carre(x=8)),"\n") # noter %05d au lieu de %5d            # à l'intérieur d'une affectation            lesCarresPlusUn <- 1 + carre(1:10)            # en tant que paramètre            lapply(X=list(a=1,b=3,c=5),FUN=carre)            Et leurs résultats : [1] 25            le carré de 8 est 00064            # non affiché : [1] 2 5 10 17 26 37 50 65 82 101            $a      [1] 1            $b      [1] 9            $c      [1] 25                  Imaginons maintenant que nous voulions écrire une fonction pvalt() qui doit renvoyer la p-value du test t de Student via l'appel de la fonction t.test(). Il faut commencer par comprendre l'objet renvoyé par la fonction t.test(), puis trouver comment extraire la composante voulue, pour ensuite écrire la fonction et enfin vérifier qu'elle renvoie bien ce qu'on voulait : # toutes les données iris            data(iris) # chargement "fainéant" (lazy loading) du data.frame iris            # juste les deux premières colonnes et les dix premières lignes            lesd <- iris[ (1:10) , (1:2) ] # plus "propre" que iris[1:10,1:2]            # effectuons le test et essayons de comprendre où est mémorisée      # la p-value            tt <- t.test(lesd)            print(tt) # après lecture, la p-value est donc 8.008e-15            # quelques essais pour comprendre ce que renvoie la fonction t.test()            print(class(tt))      print(is.list(tt))      print(names(tt))      print(tt$p.value) # c'est bien cela            # définissons rapidement la fonction demandée            pvalt <- function(test) { return( test$p.value ) }            # vérifions que c'est bien ce qu'il faut :            identical( tt$p.value, pvalt(tt) ) # doit renvoyer TRUE                  > # toutes les données iris      >      > data(iris) # chargement "fainéant" (lazy loading) du data.frame iris            > # juste les deux premières colonnes et les dix premières lignes      >      > lesd <- iris[ (1:10) , (1:2) ] # plus "propre" que iris[1:10,1:2]            > # effectuons le test et essayons de comprendre où est mémorisée      > # la p-value      >      > tt <- t.test(lesd)            > print(tt) # la p-value est donc 8.008e-15            One Sample t-test            data: lesd      t = 21.5729, df = 19, p-value = 8.008e-15      alternative hypothesis: true mean is not equal to 0      95 percent confidence interval:      3.688668 4.481332      sample estimates:      mean of x      4.085                  > print(class(tt))      [1] "htest"            > print(is.list(tt))      [1] TRUE            > print(names(tt))      [1] "statistic" "parameter" "p.value" "conf.int" "estimate" "null.value" "alternative" "method" "data.name"            > print(tt$p.value) # c'est bien cela      [1] 8.007948e-15            > # définissons la fonction demandée      >      > pvalt <- function(test) { return( test$p.value ) }            > # vérifions que c'est bien ce qu'il faut :      >      > identical( tt$p.value, pvalt(tt) ) # doit renvoyer TRUE      [1] TRUE            Une fonction anonyme correspond à la seule partie droite de définition de la fonction. Comme on l'utilise sans affectation, elle n'a pas de nom. Une telle fonction s'utilise généralement comme paramètre dans un appel de fonction. Ainsi, pour réaliser le calcul de carrés dans une liste, on peut écrire, sans passer par une fonction carre() : lapply(X=list(a=1,b=3,c=5),FUN=function(x) x*x)            Si on se rend compte qu'on utilise plusieurs fois la même fonction anonyme, il est conseillé d'en faire une fonction nommée. Cela gagne du temps et de la maintenance de code. 2. Définition et utilisation des paramètres Pour définir les paramètres d'une fonction, on doit impérativement les nommer. Par contre, il est facultatif de leur donner une valeur par défaut avec =. Mettre l'ellipse dans la définition des paramètres signifie que la fonction peut accepter (et transmettre) d'autres paramètres que ceux explicitement fournis. Voir la section 4 pour le détail sur l'ellipse. Utiliser les paramètres dans un ordre ou dans un autre peut être plus ou moins facile à mémoriser ou à comprendre. On pourra s'en rendre compte si on compare les choix de l'ordre des paramètres pour le calcul de la somme des colonnes d'une matrice via la fonction apply() dans les codes R suivants : ## calculs des sommes par colonne avec la fonction apply # pas besoin de nommer les paramètres, il s'agit de l'ordre # utilisé dans la définition de la fonction apply : apply(m,2,sum) # mieux, utilisation du nom des paramètres : apply(X=m,MARGIN=2,FUN=sum) # acceptable et reconnu par R : apply(X=m,M=2,F=sum) # sans doute la meilleure solution car elle suit # l'ordre somme colonnes matrice : apply(FUN=sum,MARGIN=2,X=m) 3. Tests des paramètres On peut tester si un paramètre est présent (ou plutôt absent) avec missing(paramètre). La liste des paramètres est fournie par formals(fonction) mais on peut aussi utiliser args(fonction) pour connaitre l'entête de la fonction ; le texte de la fonction est donné par body(fonction). Voici quelques exemples qui montrent que R est un langage assez ouvert puisqu'on peut consulter le code source du langage : > class(mean) "function" > args(mean) function (x, ...) NULL > formals(mean) $x $... > args(var) function (x, y = NULL, na.rm = FALSE, use) NULL > args(plot) function (x, y, ...) NULL > args(legend) function (x, y = NULL, legend, fill = NULL, col = par("col"), border = "black", lty, lwd, pch, angle = 45, density = NULL, bty = "o", bg = par("bg"), box.lwd = par("lwd"), box.lty = par("lty"), box.col = par("fg"), pt.bg = NA, cex = 1, pt.cex = cex, pt.lwd = lwd, xjust = 0, yjust = 1, x.intersp = 1, y.intersp = 1, adj = c(0, 0.5), text.width = NULL, text.col = par("col"), text.font = NULL, merge = do.lines && has.pch, trace = FALSE, plot = TRUE, ncol = 1, horiz = FALSE, title = NULL, inset = 0, xpd, title.col = text.col, title.adj = 0.5, seg.len = 2) NULL Il est classique de tester le type (la classe des paramètres) avec une fonction is.* et de quitter le programme avec stop ou stopifnot. Voici là encore quelques exemples issus du propre code de R : > colMeans function (x, na.rm = FALSE, dims = 1L) { if (is.data.frame(x)) x <- as.matrix(x) if (!is.array(x) || length(dn <- dim(x)) < 2L) stop("'x' must be an array of at least two dimensions") if (dims < 1L || dims > length(dn) - 1L) stop("invalid 'dims'") n <- prod(dn[1L:dims]) dn <- dn[-(1L:dims)] z <- if (is.complex(x)) .Internal(colMeans(Re(x), n, prod(dn), na.rm)) + (0+1i) * .Internal(colMeans(Im(x), n, prod(dn), na.rm)) else .Internal(colMeans(x, n, prod(dn), na.rm)) if (length(dn) > 1L) { dim(z) <- dn dimnames(z) <- dimnames(x)[-(1L:dims)] } else names(z) <- dimnames(x)[[dims + 1]] z } <bytecode: 0x3809668> <environment: namespace:base> > var function (x, y = NULL, na.rm = FALSE, use) { if (missing(use)) use <- if (na.rm) "na.or.complete" else "everything" na.method <- pmatch(use, c("all.obs", "complete.obs", "pairwise.complete.obs", "everything", "na.or.complete")) if (is.na(na.method)) stop("invalid 'use' argument") if (is.data.frame(x)) x <- as.matrix(x) else stopifnot(is.atomic(x)) if (is.data.frame(y)) y <- as.matrix(y) else stopifnot(is.atomic(y)) .Call(C_cov, x, y, na.method, FALSE) } <bytecode: 0x46f7258> <environment: namespace:stats> 4. L'ellipse notée ... Comme le montrent les exemples précédents, un argument possible pour une fonction est l'ellipse, qui se note ... (trois points qui se suivent) et dont l'aide est ici. Cette notation, qui se révèle très pratique à l'usage, permet de ne pas spécifier tous les paramètres à utiliser et de laisser le soin à R de les transmettre. L'ellipse sert beaucoup lorsqu'on écrit une fonction de tracé graphique et pour implémenter des fonctions génériques. Les paramètres qu'on définit sont les plus usuels et l'ellipse permet de passer les moins fréquents. Imaginons par exemple que l'on veuille interfacer la fonction boxplot() avec un titre et une unité obligatoires. Voici la trame d'une telle fonction : boxplot_UN <- function(titre,x,unite) { if (missing(titre)) { cat(" syntaxe : boxplot_UN(titre,x,unite) \n") cat(" titre et unite sont obligatoires.\n\n") return(invisible(NULL)) } # fin si if (missing(unite)) { stop("vous devez donner l'unité utilisée.\n") } # fin si # suite du code de boxplot_UN } # fin de fonction boxplot_UN ############################################################### > boxplot_UN() syntaxe : boxplot_UN(titre,x,unite) titre et unite sont obligatoires. > boxplot_UN("oui",1:10) Erreur dans boxplot_UN("oui", 1:10) : vous devez donner l'unité utilisée. > boxplot_UN("oui",1:10,"kilos") # OK... Il est clair qu'avec une telle fonction on ne peut pas modifier les bornes xlim et ylim du tracé, par exemple. Au lieu de les rajouter comme arguments, le mieux est d'ajouter l'ellipse. Dès lors, l'utilisateur a accès à toutes les options de boxplot : boxplot_DEUX <- function(titre,x,unite,...) { if (missing(titre)) { cat(" syntaxe : boxplot_DEUX(titre,x,unite,...) \n") cat(" titre et unite sont obligatoires.\n\n") return(invisible(NULL)) } # fin si if (missing(unite)) { stop("vous devez donner l'unité utilisée.\n") } # fin si # suite du code de boxplot_DEUX } # fin de fonction boxplot_DEUX ############################################################### > boxplot_UN("oui",1:10,"k",ylim=c(0,10)) Erreur dans boxplot_UN("oui", 1:10, "k", ylim = c(0, 10)) : argument inutilisé (ylim = c(0, 10)) > boxplot_DEUX("oui",1:10,"k",ylim=c(0,10)) # OK... 5. Quelques exemples de fonctions Afin de vous entrainer à bien "parler fonction en R", voici quatres exemples qui mettent en pratique tout ce que nous venons de décrire. Nous montrerons au passage comment "progresser" dans l'écriture d'une fonction. 5.1 La fonction moyenne() Pour implémenter une fonction nommée moyenne() -- aussi bizarre que cela puisse paraitre à une ou un néophyte, cette définition est plus rapide que la "vraie" fonction mean() de R pour des petits vecteurs numériques -- le code minimal est le suivant : moyenne <- function(x) sum(x)/length(x) Cet exemple de définition est suffisant dans l'environnement de R, en mode interactif, si on est pressé de tester la fonction. Toutefois, il vaut mieux mettre un commentaire pour détailler ce que fait la fonction et utiliser explicitement le mot return() pour indiquer ce qui est renvoyé : # la fonction moyenne, version 2, plus explicite moyenne <- function(x) { # calcul de la moyenne arithmétique return( sum(x)/length(x) ) } # fin de fonction moyenne Après réflexion, vous pourrez vous rendre compte que l'argument de moyenne() doit être numérique, car sinon la fonction sum() échoue. De même, s'il y a des NA dans les valeurs, la fonction sum() échoue aussi. D'où une version 3, plus stable et plus complète pour la moyenne, avec au passage une séparation du calcul du renvoi de la valeur calculée : # la fonction moyenne, version 3 et complète moyenne <- function(x,oteNA=FALSE) { # calcul de la moyenne arithmétique # après suppression éventuelle des valeurs NA stopifnot(is.numeric(x)) if (oteNA) { x <- na.omit(x) } # calcul valMoy <- sum(x)/length(x) # renvoi return( valMoy ) } # fin de fonction moyenne Vous aurez compris, au vu de cette progression, qu'écrire une fonction ne se fait pas forcément du premier jet. Le nom et le choix de la valeur par défaut du paramètre oteNA pour supprimer les valeurs NA devrait aussi être détaillé. Nous avons ici pris le parti de reproduire la valeur par défaut de la fonction mean(), mais sans utiliser le même nom de paramètre que R utilise, à savoir na.omit, ce qui est un petit peu maladroit (volontairement). 5.2 La fonction médiane() Forts de notre expérience avec la fonction moyenne() précédente, nous pourrions être tentés d'écrire de suite un "beau" code "stable et complet" pour la fonction mediane() comme ceci : # la fonction mediane, version 1 mediane <- function(x,na.rm=FALSE) { # calcul de la médiane # après suppression éventuelle des valeurs NA # vérifions que x est numérique stopifnot(is.numeric(x)) # supprimons les valeurs NA si demandé if (na.rm) { x <- na.omit(x) } # tri des valeurs x <- sort(x) # avec un nombre impair de termes, la médiane est # au milieu de la liste des valeurs, sinon c'est # la moyenne arithmétique des deux valeurs au centre # de la liste lng <- length(x) lng2 <- lng/2 if ((lng %% 2)==1) { # cas impair return( x[ 1 + round(lng2) ] ) } else { return( mean(x[ c(lng2,lng2+1) ]) ) } # fin si } # fin de fonction mediane C'est sans doute une "belle" fonction, mais elle est incomplète, parce que la médiane peut se calculer sur des vecteurs de caractères avec un nombre pair de termes. On remarquera que nous avons désormais écrit pour le paramètre na.rm au lieu de oteNA comme pour la fonction moyenne() précédente. C'est sans doute mieux, car cela aide à se rappeler comment on écrit cela dans les autres fonctions standards de R. Programmer, c'est aussi évoluer, changer d'avis, à condition de le dire et de rester cohérent avec les autres fonctions de R ! 5.3 La fonction decritColonne() R fournit de nombreuses fonctions pour décrire une variable quantitative comme le poids, ou la taille. Il y a les fonctions élémentaires comme mean(), sd() et des fonctions plus complètes comme summary() ou fivenum(). Toutes ces fonctions ont un gros défaut : elles n'indiquent pas l'unité. Ainsi voir une taille de 5,6 pour des adultes peut apparaitre comme une erreur pour un français. Avec l'indication 5,6 pieds, ce serait mieux car vu qu'un pied fait 30,47 centimètres la valeur 5,6 pieds correspond approximativement à 170,6 cm, ce qui montre bien qu'il ne s'agit pas d'une erreur. Nous nous proposons ici d'ajouter une unité à la description statistique classique et de considérer ce paramètre comme obligatoire. Nous allons nous focaliser sur les descripteurs de tendance centrale que sont la moyenne et la médiane, et sur les valeurs de controle -- il faudrait bien sûr ajouter des indicateurs de dispersion absolue et relative, comme l'écart-type, la distance interquartile, le coefficient de variation... pour être plus complet -- que sont le minimum et le maximum afin de rester dans des calculs simples et compréhensibles. Nous ne fournissons pas non plus de code pour représenter graphiquement les données et ces indicateurs mais ce serait indispensable s'il s'agissait d'écrire une "vraie" fonction statistique de description d'une variable quantitative dont on connait l'unité. Comme programmer, c'est se rappeler des programmes déjà écrits, nous refuserons bien évidemment d'appliquer la fonction à des données qui ne sont pas numériques. Voici un code possible pour cette fonction : # une description quantitative avec unité obligatoire # après suppression éventuelle automatique des valeurs NA decritColonne <- function(x,unite="") { stopifnot(is.numeric(x)) if (unite=="") { stop(" le paramètre unite est obligatoire.\n") } # fin si nbNA <- sum(is.na(x)) # gestion des NA nbOrg <- length(x) x <- na.omit(x) nbVal <- length(x) # préparation des colonnes pour la mise en forme nomCalcs <- c("nbOrg","nbNA","nbVal","min","moyenne","médiane","max") nbCalc <- length(nomCalcs) unites <- c( rep("valeurs",3), rep(unite,nbCalc-3) ) # calculs calcs <- c( nbOrg, nbNA, nbVal, min(x),mean(x),median(x),max(x) ) resDf <- data.frame( round(calcs),unites,row.names=nomCalcs) names(resDf)[1] <- "resultats" # affichage print(resDf,quote=FALSE) # renvoi invisible (mais "caisse queue sait" ?) return( invisible(resDf) ) } # fin de fonction decritColonne Le choix du nom des variables et des fonctions est important. Ici, decritColonne() est sans doute maladroit et decritQuantitative() aurait été plus approprié. Toutefois, il est possible que l'utilisation principale de cette fonction soit d'être appelée par une fonction plus générale, nommée par exemple decritColonnes() -- donc avec un s en plus à la fin -- et là, le nom de la fonction se justifie tout à fait. Voici un exemple d'utilisation : > data(iris) ; decritColonne(iris$Sepal.Length,"cm") resultats unites nbOrg 150 valeurs nbNA 0 valeurs nbVal 150 valeurs min 4 cm moyenne 6 cm médiane 6 cm max 8 cm 5.4 La fonction plotCouleur() Il est très courant d'avoir à coloriser des points dans un tracé, par exemple pour repérer les hommes et les femmes dans une étude épidémiologique. Nous présentons ici une fonction dont la syntaxe est plotCouleur(x,y,facteur,couleurs). Ainsi, pour tracer le poids en fonction de l'age avec la couleur bleue pour les garçons et rouge pour les filles, on réaliserait l'appel plotCouleur(age,poids,sexe,c("blue","red")) ou, si astucieusement on dispose d'une liste de couleurs par défaut, l'appel peut se résumer à plotCouleur(age,poids,sexe). Voici la fonction : plotCouleur <- function(x,y,facteur,couleurs,...) { if (missing(couleurs)) { couleurs <- c("blue","red","green","black","yellow") } # finsi # conversion silencieuse en facteur # (permet d'utiliser une liste de nombres comme facteur) if (!is.factor(facteur)) { facteur <- factor(facteur) } # fin si # vérification du nombre de couleurs nbMod <- nlevels(facteur) if (nbMod>length(couleurs)) { stop(paste("vous devez fournir",nbMod,"couleurs pour le tracé.\n")) } # finsi # couleurs à utiliser couls <- couleurs[ as.numeric(facteur) ] # tracé plot(x,y,col=couls,pch=19,...) } # fin de fonction plotCouleur Vous aurez remarqué, bien sûr, que nous avons utilisé l'ellipse. Attention toutefois : R n'autorise pas de spécifier plusieurs fois le même paramètre. Ainsi, puisque nous utilisons déjà le paramètre pch, l'appel suivant est incorrect > plotCouleur(age,taille,sexe,c("green","pink"),pch=17) Error in localWindow(xlim, ylim, log, asp, ...) : argument formel "pch" correspondant à plusieurs arguments fournis 6. Spécificités du langage R R est très différent des autres langages par rapport aux fonctions : les fonctions sont nativement vectorielles si les calculs utilisés sont vectoriels, ou si on y fait appel à d'autres fonctions vectorielles. les fonctions sont des objets comme les autres et peuvent être passés en paramètres : ## utilisation de fonctions en paramètres f <- function(x) { return(paste("calcul de f(",x,")\n")) } g <- function(x) { return(paste("calcul de g(",x,")\n")) } condition <- TRUE # affichera : calcul de f( 3 ) ifelse( condition, f, g ) ( 3 ) les paramètres sont nommés et ils peuvent avoir des valeurs par défaut, ce qui fournit une très grande souplesse d'utilisation (et un casse-tête pour les mémoriser). Par contre ce nommage n'est pas normalisé et ne peut pas l'être, compte tenu des structures de données de R : > args(apply) function (X, MARGIN, FUN, ...) NULL > args(tapply) function (X, INDEX, FUN = NULL, ..., simplify = TRUE) NULL > args(mapply) function (FUN, ..., MoreArgs = NULL, SIMPLIFY = TRUE, USE.NAMES = TRUE) NULL > args(vapply) function (X, FUN, FUN.VALUE, ..., USE.NAMES = TRUE) NULL > args(lapply) function (X, FUN, ...) NULL > args(rapply) function (object, f, classes = "ANY", deflt = NULL, how = c("unlist","replace", "list"), ...) NULL   Partie 6 - Eviter de programmer en R   Table des matières cliquable   1. Via les fonctions de base déjà existantes   2. Via les packages   3. Eviter de programmer des boucles avec la famille *apply*   4. Apprendre les actions courantes en R   5. Comment survivre à R ? 1. Via les fonctions de base déjà existantes Lorsqu'on débute en programmation, il est bon d'apprendre à savoir tout faire, tout calculer. Par exemple pour les statistiques usuelles, il faut savoir effectuer un calcul de moyenne, de médiane, d'écart-type. Il faut avoir écrit au moins une fois dans sa vie la recherche du minimum, du maximum dans un vecteur, avec leur nombre d'ocurrences et leurs positions pour commencer à savoir programmer. Savoir programmer, c'est ensuite savoir utiliser les programmes des autres, donc ne pas réinventer la roue, l'eau tiède, etc. R dispose de nombreuses fonctions de base en standard, via les packages base, stats, graphics et utils : package nbObjets liste base 1167    lls_base.sor stats 493    lls_stats.sor graphics 87    lls_graphics.sor utils 198    lls_utils.sor Apprendre à programmer en R consiste donc à passer beaucoup de temps, au moins au début, pour savoir ce que R sait déjà faire -- et il en fait déjà beaucoup. Car tous les traitements de données usuels (transformations, recodages, discrétisation, fusion...) ont déjà été passés en revue, analysés, programmés, parfois de façon très sophistiquée. On pourra consulter les fonctions transform() et stack() pour s'en rendre compte. De même, puisque R est un logiciel pour les calculs statistiques, tous les calculs usuels et même les calculs récents en statistique, bioinformatique, etc. sont déjà implémentés en R. Une grande conclusion est qu'il faut passer du temps avant de «maitriser la bête». L'expérience prouve qu'on y gagne en vitesse de développement et en compréhension du fonctionnement du langage R. Soyons clairs : sauf si vous inventez une nouvelle méthode de calcul en statistiques, vous n'avez pas à programmer le moindre calcul statistique en R. Vous avez à lire les données, appeler les fonctions de R qui calculent, vous avez à mettre en forme les résultats, mais vous n'avez pas à programmer le moindre calcul statistique en R (redite volontaire). 2. Via les packages Plus encore que les deux mille et quelques fonctions des quatre packages de la section précédente, c'est la foultitude des packages spécialisés qui fait la richesse de R et qui le rend incomparable pour les calculs et les graphiques statistiques. Même si d'autres langages peuvent être considérés comme "plus beaux", "plus propres", "plus efficaces", disons comme Ruby, Python, Java, C..., aucun autre langage de programmation n'est aussi complet dès qu'il s'agit de graphiques et de calculs statistiques. La preuve : ces langages ont préféré développer des interfaces de dialogue avec R plutôt que de réimplémenter les mêmes calculs et graphiques. C'est ainsi qu'on trouve rpy, rinruby, rJava, Rcpp... Il suffit de consulter chaque jour la liste des packages ajoutés quotidiennement pour constater que le nombre de packages grandit vraiment très vite et qu'aucun autre langage ne croit aussi vite... Même dans certains domaines où on pourrait ne pas l'y attendre, R se révéle performant grâce à son aspect vectoriel. Le package XML et le livre associé en sont un très bon exemple.            Au passage, l'un des points forts de R est la mise en forme ou la restructuration des données. On pourra consulter les packages plyr et reshape2 pour s'en rendre compte 3. Eviter de programmer des boucles avec la famille *apply* Programmer des calculs, des affichages revient souvent à appliquer un même traitement à de nombreux "objets". Dans la mesure où R distingue les vecteurs, les matrices et les listes (dont les data frames), il n'est pas étonnant que ce mot appliquer se décline en plusieurs versions suivant les structures de données : > cbind(apropos("apply")) [1,] "apply" [2,] "dendrapply" [3,] "eapply" [4,] "kernapply" [5,] "lapply" [6,] "mapply" [7,] ".mapply" [8,] "rapply" [9,] "sapply" [10,] "tapply" [11,] "vapply" La fonction apply() utilise des objets "matrice". Sa syntaxe de base utilise les paramètres X qui est la matrice ou un objet assimilable à une matrice, FUN la fonction à appliquer, qu'elle soit nommée ou anonyme et MARGIN pour préciser si on applique la fonction dans le sens des lignes (MARGIN=1) ou des colonnes (MARGIN=2). La fonction lapply() utilise une liste nommée X et lui applique la fonction FUN élément par élément. L'objet renvoyé est une liste. La fonction sapply() exécute lapply() et en simplifie la sortie pour renvoyer un vecteur ou une matrice. sapply utilise donc les mêmes paramètres que lapply. La fonction rapply() exécute récursivement son paramètre f sur son autre paramètre object, ce que ne savent pas faire les fonctions précédentes. La fonction tapply() permet de découper le paramètre X selon le paramètre INDEX avant d'appliquer son paramètre FUN à chaque découpage obtenu. C'est donc en quelque sorte l'enchainement de split() et lapply(). La fonction vapply permet de préciser à sapply quel type de données on obtiendra en sortie. La fonction mapply() travaille en "multivarié". Notre cours 1 de programmation R avancée, exercice 5 et sa solution montre par l'exemple comment utiliser ces fonctions. 4. Apprendre les actions courantes en R S'il n'est pas possible de tout apprendre en R, il est facile de prévoir un planning et un ordre pour apprendre les actions courantes en R : On commence presque toujours par lire des données. Donc tout ce qui se nomme read.* est bon à prendre et à apprendre, dont la lecture des fichiers Excel, des fichiers PDF ou autres fichiers XML ou Fasta...Si on ne lit pas des fichiers, c'est qu'on lit des bases de données ou qu'on simule des données. Là encore les packages de R sont faciles à trouver qui remplissent ces tâches, par exemple avec R Site Search... > apropos("read") readBin readChar readCitationFile read.csv read.csv2 read.dcf read.delim read.delim2 read.DIF read.fortran read.ftable read.fwf readline readLines readRDS .readRDS readRenviron read.socket read.table Sys.readlink > ls("package:gdata") aggregate.table ans Args as.levelsMap as.listLevelsMap as.object_size bindData case cbindX centerText combine ConvertMedUnits drop.levels duplicated2 elem env frameApply getDay getHour getMin getMonth getSec getYear humanReadable installXLSXsupport interleave is.levelsMap is.listLevelsMap is.object_size isUnknown is.what keep ll lowerTriangle lowerTriangle<- ls.funs mapLevels mapLevels<- matchcols NAToUnknown nobs nPairs object.size read.xls remove.vars rename.vars reorder.factor resample sheetCount sheetNames startsWith trim trimSum unknownToNA unmatrix upperTriangle upperTriangle<- wideByFactor write.fwf xls2csv xls2sep xls2tab xls2tsv xlsFormats Avec des données, on effectue des calculs, on produit des graphiques. Les task views du CRAN permettent de s'y retrouver. Pour celles et ceux qui travaillent dans le domaine de la bioinformatique, on rajoutera les pages Explore packages et help de bioconductor. Une fois maitrisés les calculs élémentaires, vous pouvez aborder les modélisations classiques qui reposent sur le modèle linéaire (soit la fonction lm()) et sa généralisation (soit la fonction glm()) soit basculer vers le non linéaire, par exemple avec la fonction nlm() ou des fonctions comme loess() ou lowess(). > apropos("lm") allQLm .__C__anova.glm .__C__anova.glm.null .__C__glm .__C__glm.null .__C__lm .__C__mlm colMaxs colMeans .colMeans colMedians colMins confint.lm contr.helmert .__C__optionalMethod dummy.coef.lm getAllMethods glm glm.control glm.fit KalmanForecast KalmanLike KalmanRun KalmanSmooth kappa.lm lm .lm.fit lm.fit lm.influence lm.wfit modelesCLMMetavir model.matrix.lm nlm nlminb predict.glm predict.lm residuals.glm residuals.lm summary.glm summary.lm > apropos("ova") anova .__C__anova .__C__anova.glm .__C__anova.glm.null manova power.anova.test stat.anova summary.manova Pour les tests, R implémente "tout ce qui bouge" et plus si affinités, ce qui se nomme plus ou moins *.test() ou anova() : > apropos("test") "ansari.test" "bartlett.test" "binom.test" "Box.test" "chisq.test" "cor.test" "file_test" "fisher.test" "fligner.test" "friedman.test" "kruskal.test" "ks.test" "mantelhaen.test" "mauchly.test" "mcnemar.test" "mood.test" "oneway.test" "pairwise.prop.test" "pairwise.t.test" "pairwise.wilcox.test" "poisson.test" "power.anova.test" "power.prop.test" "power.t.test" "PP.test" "prop.test" "prop.trend.test" "quade.test" "shapiro.test" "testInheritedMethods" "testPlatformEquivalence" "testVirtual" "t.test" ".valueClassTest" "var.test" "wilcox.test" > apropos("anova") "anova" ".__C__anova" ".__C__anova.glm" ".__C__anova.glm.null" "manova" "power.anova.test" "stat.anova" "summary.manova" Il faut ensuite mettre en forme les calculs, produire des rapports, intégrer les graphiques, exporter vers des formats classiques comme les précédents (Excel, PDF, base de données, XML...). Donc il faut approfondir tout ce qui se nomme write.* et tout ce qui se trouve dans le package gdata. > apropos("write") aspell_write_personal_dictionary_file .rs.defaultLibPathIsWriteable .rs.ensureWriteableUserLibrary .rs.isLibraryWriteable .rs.writeableLibraryPaths RtangleWritedoc RweaveLatexWritedoc write writeBin writeChar write.csv write.csv2 write.dcf write.ftable writeLines write.socket write.table > library(XML) > ls("package:XML") addAttributes addChildren addNode addSibling append.xmlNode append.XMLNode asXMLNode asXMLTreeNode catalogAdd catalogClearTable catalogDump catalogLoad catalogResolve coerce comment.SAX COMPACT compareXMLDocs docName docName<- Doctype DTDATTR dtdElement dtdElementValidEntry dtdEntity dtdIsAttribute DTDLOAD DTDVALID dtdValidElement endElement.SAX ensureNamespace entityDeclaration.SAX findXInclude free genericSAXHandlers getChildrenStrings getDefaultNamespace getEncoding getHTMLExternalFiles getHTMLLinks getLineNumber getNodeLocation getNodePosition getNodeSet getRelativeURL getSibling getXIncludes getXMLErrors htmlParse htmlTreeParse HUGE isXMLString libxmlFeatures libxmlVersion makeClassTemplate matchNamespaces names.XMLNode newHTMLDoc newXMLCDataNode newXMLCommentNode newXMLDoc newXMLDTDNode newXMLNamespace newXMLNode newXMLPINode newXMLTextNode NOBASEFIX NOBLANKS NOCDATA NODICT NOENT NOERROR NONET NOWARNING NOXINCNODE NSCLEAN OLD10 OLDSAX parseDTD parseURI parseXMLAndAdd PEDANTIC processingInstruction.SAX processXInclude readHTMLList readHTMLTable readKeyValueDB readSolrDoc RECOVER removeAttributes removeChildren removeNodes removeXMLNamespaces replaceNodes saveXML SAX1 schemaValidationErrorHandler setXMLNamespace show source startElement.SAX supportsExpat supportsLibxml text.SAX toHTML toString.XMLNode XINCLUDE xml xmlAncestors xmlApply xmlAttributeType xmlAttrs xmlAttrs<- xmlCDataNode xmlChildren xmlChildren<- xmlCleanNamespaces xmlClone xmlCodeFile xmlCommentNode xmlContainsElement xmlContainsEntity xmlDeserializeHook xmlDoc xmlDOMApply xmlElementsByTagName xmlElementSummary xmlErrorCumulator xmlEventHandler xmlEventParse xmlGetAttr xmlHandler xmlHashTree xmlInternalTreeParse xmlName xmlName<- xmlNamespace xmlNamespace<- xmlNamespaceDefinitions xmlNamespaces xmlNamespaces<- xmlNativeTreeParse xmlNode xmlOutputBuffer xmlOutputDOM xmlParent xmlParent<- xmlParse xmlParseDoc xmlParserContextFunction xmlParseString xmlPINode xmlRoot xmlSApply xmlSchemaParse xmlSchemaValidate xmlSearchNs xmlSerializeHook xmlSize xmlSize.default xmlSource xmlSourceFunctions xmlSourceSection xmlStopParser xmlStructuredStop xmlTextNode xmlToDataFrame xmlToList xmlToS4 xmlTree xmlTreeParse xmlValue xmlValue<- xmlXIncludes xpathApply xpathSApply 5. Comment survivre à R ? Malheureusement, la richesse de R en fait aussi son plus gros défaut. Il faut apprendre une grosse centaine de fonctions (et leurs paramètres) avant de commencer à écrire des programmes concis, il faut désapprendre les boucles dans un certain nombre de cas avant de bien profiter des aspects vectoriels de R, il faut être à l'aise avec les méthodes statistiques pour s'y retrouver facilement dans les packages et les options implémentées, bref ce n'est pas une mince affaire que de bien programmer en R. Heureusement, avec «du coeur à l'ouvrage» et de nombreuses heures d'entrainement, on y arrive toujours !   Partie 7 - Programmation soutenue   Table des matières cliquable   1. Structure de données classiques des autres langages   2. Problèmes demandant des compétences techniques en algorithmique   3. Problèmes de grande taille (big data)   4. Problèmes de grande ampleur (big computing)   5. La récursivité 1. Structure de données classiques des autres langages Lorsqu'on suit des cours de programmation, on apprend des techniques classiques et des modèles de résolution de problèmes, nommés en anglais Design Patterns. On apprend aussi à utiliser des structures de données adaptées, comme les piles, les queues, les files, les graphes (dont les arbres), les listes chainées, les tableaux associatifs... Il faut donc de nombreuses heures de cours et de pratique avant de maitriser la programmation. Les cours présentés ici ne peuvent prétendre se substituer à ces enseignements traditionnels, tout au plus sensibiliser à l'importance de ces concepts via quelques exemples choisis. On trouvera donc dans les exercices de ce cours des graphes, des arbres et des tableaux associatifs à titre d'illustration. Il faut noter aussi que l'utilisation de R est souvent liée à des calculs statistiques, discipline qui a ses propres structures comme les séries chronologiques, les variables ordinales, les matrices de distances, les arbres de classification hiérarchique... et ses propres méthodes comme le modèle linéaire, les intervalles de confiance... 2. Problèmes demandant des compétences techniques en algorithmique Voici un problème qui a l'air presque anodin : quelle est la plus grande sous-chaine de caractères répétée dans une chaine de caractères ? Attention : il ne s'agit pas de trouver la lettre la plus souvent utilisée, mais une sous-chaine. Pour un texte "littéraire", avec des avec des "vrais" mots, c'est facile à faire et rapide. Voir par exemple le site analexies. Mais pour une séquence d'ADN comme celle de Pseudomonas putida GB-1 (soit un peu plus de 6 millions de lettres), comment faire ? C'est grâce à l'étude de structures de données adaptées comme celle de tableau des suffixes que le problème se résoud de façon « assez rapide » (quelques dizaines de secondes sur un ordinateur récent un peu puissant, pour Pseudomonas putida GB-1). Il est clair qu'une structure comme celle-là ne s'invente pas en pensant dix minutes au problème. C'est pourquoi il y a un moment où savoir programmer dans un langage ne suffit plus : il faut aussi savoir inventer des algorithmes, connaitre les algorithmes classiques et les structures de données associées. Voici deux références pour progresser dans ce domaine : Algorithmique et Programmation JAVA : un polycopié en français de polytechnique (version locale) ; Algorithms : une grande référence anglaise sur les algorithmes. 3. Problèmes de grande taille (big data) Lorsque les données sont très importantes (disons quelques dizaines de giga octets ou tera octets), ce qui est souvent le cas en bioinformatique, en [méta]génomique, de nouvelles difficultés surgissent : il n'est plus possible de charger les données en mémoire, ou seulement partiellement, les calculs ne peuvent plus s'exécuter sur un seul ordinateur et il faut recourir à un cluster ou à une grid de calculateurs... La programmation en "grande dimension" (autre nom du big data) nécessite des approches algorithmiques différentes de la programmation classique. Ce sujet est beaucoup trop technique pour pouvoir être abordé dans un cours comme celui-ci qui est une petite introduction à la programmation classique, mais il est bon de savoir qu'il existe des solutions, par exemple Revolution R, qu'on y parle Hadoop et autres map/reduce ou map/filter/reduce, de la programmation fonctionnelle. 4. Problèmes de grande ampleur (big computing) Contrairement à un problème de grande taille, un problème de grande ampleur peut avoir des données de taille «raisonnable» mais leur traitement nécessite des capacités gigantesques. Un exemple classique est la détermination (calcul ?) de sous-séquences répétées à ne pas confondre avec le calcul de sous-chaines répétées (qui, lui, se traite «assez facilement»). Dans les phrases un bateau qui va sur l'eau et mon ami est en bateau, la chaine eau est une sous-chaine répétée. Dans les phrases mon papa est dans un bateau et pour mon tonton, il y a un souci, la sous-séquence notée mon*un, qui signifie le mot mon suivi quelque part du mot un, est une sous-séquence répétée. Ce genre de problème est classique lorsqu'on s'intéresse aux séquences d'ADN ou d'acides aminés. Là encore, la programmation en "grande complexité" (autre nom pour dire grande ampleur) nécessite des approches algorithmiques différentes de la programmation classique. Ce sujet est beaucoup trop technique pour pouvoir être abordé dans un cours comme celui-ci qui est une petite introduction à la programmation classique, mais il est bon de savoir qu'il n'existe pas toujours des solutions exactes et qu'on doit alors se contenter de résultats approchés, d'approximations souvent issues d'heuristiques voire de métaheuristiques... 5. La récursivité Programmer, c'est écrire des programmes. De nombreux programmes utilisent des fonctions. Il y a parfois des façons "naturelles" ou "élégantes" de traiter un problème. Par exemple, voici une méthode de tri : Pour trier une liste de valeurs par ordre décroissant, il suffit de trouver le plus grand élément de la liste, de l'afficher, puis de l'enlever de la liste et de trier la liste restante par ordre décroissant, jusqu'à ce qu'il n'y ait plus de valeurs à trier. Cette définition du tri qui fait référence à son propre tri se nomme un appel récursif. Ecrire des fonctions récursives, savoir quand les utiliser et comment s'en passer ou comment les convertir en fonctions non récursives (lorsque c'est concrètement faisable) est une partie non négligeable de l'algorithmique traditionnelle. Pour aller plus loin dans ce sujet, on pourra consulter le cours d'algorithmique de F. Vivien, chapitre 3 (version locale) et la définition de la fonction d'Ackermann qui est, en principe, dérécursivable...   Partie 8 - Déboggage, profilage et optimisation   Table des matières cliquable   1. But de cette section   2. Un comportement bizarre de R   3. Déboggage   4. Ecrire <<- n'est pas une faute de frappe   5. Profilage   6. Optimisation 1. But de cette section Nous allons dans cette page essayer de répondre à trois questions : Mon programme ne fonctionne pas comme je le voudrais. Où est l'erreur ? Mon programme est lent. Quelle partie du code est la plus lente ? Comment accélérer le code qui est lent ? R fournit des outils qui permettent de répondre aux deux premières questions car après tout, il ne s'agit que d'analyser le code du programme ou son exécution. Par contre, c'est à vous de modifier le code pour le rendre plus rapide sachant que de par sa conception, R est "lent". Il est aussi possible que votre problème à traiter soit un problème "difficile", NP-complet ou qu'il "explose combinatoirement", ce qui signifie que de toutes façons il sera très très long à exécuter (si vous avez le choix, n'hésitez pas à essayer de programmer ce genre de problèmes : comme c'est long, on peut passer beaucoup de temps à la machine à café sans culpabiliser de peur de rater la fin de l'exécution du programme !). Nous essaierons de fournir pour cette dernière partie quelques pistes de solutions, lorsqu'il doit être possible d'accélérer l'exécution, ce qui n'est pas toujours le cas... Mais commençons par un programme qui semble à la fois fonctionner et ne pas fonctionner, et qui, en tous cas, ne s'arrête pas dès le début de l'exécution. Il ne s'agit donc pas d'un problème simple à résoudre ou d'une erreur naïve de programmation. 2. Un comportement bizarre de R Il est rare qu'un programme "marche" du premier coup. Parfois, même si on est convaincu que R va faire ce qu'on lui demande et qu'à la main on pense avoir résolu le problème, R semble se comporter bizarrement. Voici un exemple de programme un peu "surprenant". On demande à R de créer une matrice avec deux lignes et deux colonnes. L'utilisateur peut alors supprimer la ligne ou la colonne de son choix et voir ce qu'il reste de la matrice. Mais bizarrement, R a l'air de "perdre" la matrice avant la fin... Le code R associé, fourni ci-dessous, est court, simple à lire et à comprendre. # un comportement bizarre de R # 1. une matrice 2x2 a priori toute simple mat <- matrix(1:4,nrow=2) cat("\nVoici la matrice au départ,\n") cat("avec",nrow(mat),"lignes et",ncol(mat),"colonnes\n") print(mat) # 2. suppression interactive de ligne ou de colonne rep <- "OK" while (rep=="OK") { cat(" taper L pour supprimer une ligne, ") cat(" ou C pour supprimer une colonne, ") nature <- readline() objet <- ifelse(nature=="L","ligne","colonne") cat(" en quelle position ? ") position <- as.numeric(readline()) if (objet=="ligne") { mat <- mat[ -position, ] } else { mat <- mat[ ,-position ] } # finsi cat("Après suppression de la ",objet,"numéro",position,"\n") cat("on dispose de la matrice suivante,\n") cat("avec",nrow(mat),"lignes et",ncol(mat),"colonnes\n") print(mat) } # fin tant que Mais l'exécution de ce code est un peu "mystérieuse" : Voici la matrice au départ, avec 2 lignes et 2 colonnes [,1] [,2] [1,] 1 3 [2,] 2 4 taper L pour supprimer une ligne, ou C pour supprimer une colonne, L en quelle position ? 1 Après suppression de la ligne numéro 1 on dispose de la matrice suivante, avec lignes et colonnes [1] 2 4 taper L pour supprimer une ligne, ou C pour supprimer une colonne, C en quelle position ? 1 Error in mat[, -position] : nombre de dimensions incorrect Il semblerait que R n'arrive plus à trouver le nombre de lignes et de colonnes de la matrice car au niveau de la dernière suppression, juste avant l'erreur, il y a affiché "avec lignes" mais aucun nombre de lignes n'est affiché. Pour un(e) professionnel(le) de R , ce comportement est normal car il est décrit dans l'aide (longue, très longue) de la fonction [() et dans l'aide de la fonction drop() obtenues par help("[") et help(drop). Sauf que les explications -- en anglais -- ne sont pas très explicites : extrait de help("["]) --------------------- parameter drop: For matrices and arrays. If 'TRUE' the result is coerced to the lowest possible dimension. extrait de help(drop) --------------------- Array subsetting ('[') performs this reduction unless used with 'drop = FALSE', but sometimes it is useful to invoke 'drop' directly. Pour essayer de comprendre ce qui se passe, on peut tenter d'aller à la pêche (sous-entendu "aux informations") à l'aide de la fonction print() via print(mat) ou de print(nrow(mat)). Cela se révèlera sans doute difficile et peu productif parce que si x n'est pas une matrice, nrow(x) renvoie NULL. Est-ce un problème ? Oui, mais c'est un peu subtil. Si R affiche bien NULL pour NULL avec print(), concaténer NULL avec quelque chose transforme NULL en chaine vide. De même, utiliser NULL dans cat() renvoie aussi la chaine vide, et du coup on ne voit plus rien. Voici avec un exemple pourquoi il est difficile de comprendre ce qui se passe avec un simple print() : > print(NULL) NULL > cat(NULL) > print(nrow(matrix(nrow=4))) [1] 4 > cat(nrow(matrix(nrow=4)),"colonnes\n") 4 colonnes > cat(nrow(vector(length=4)),"colonnes\n") colonnes Donc si on ne voit rien avec un print() de notre objet, il faudrait sans doute essayer un print(class(mat)). Et là, miracle ! Voici la partie du code qui a été légèrement modifié cat("Après suppression de la ",objet,"numéro",position,"\n") cat("on dispose d'une structure ",class(mat),"\n") et l'affichage de l'exécution : ... Après suppression de la ligne numéro 1 on dispose d'une structure integer [1] 2 4 ... Nous avons donc identifié le problème : la variable mat change de nature. De "matrix" elle passe à "integer", ce qui signifie vecteur d'entiers. Avec un peu plus d'entrainement, c'était visible puisque R avait écrit, avec un seul indice [1] 2 4 au lieu de l'affichage classique des matrices, avec deux séries d'indices : [,1] [,2] [1,] 2 4 Mais quand on débute en R , on n'est pas expert(e), bien sûr et ces subtilités d'affichage nous échappent souvent. Nous avons donc identifié l'erreur, ou du moins nous avons cerné le problème. Pour le résoudre, l'aide de [() et de drop() indiquent clairement qu'il faut empêcher R de réduire la dimension à l'aide du paramètre drop. Donc en écrivant dans notre code if (objet=="ligne") { mat <- mat[ -position,, drop=FALSE ] } else { mat <- mat[ ,-position, drop=FALSE ] } # finsi le problème est résolu. Ouf ! Enfin, presque... comme souvent en programmation. Car du coup notre boucle... boucle ! Il faut donc prévoir d'arrêter de demander à supprimer des lignes ou des colonnes s'il n'y en a plus, soit le code suivant juste avant la fin de la boucle tant que : if ((nrow(mat)==0)|ncol(mat)==0) { cat("il n'y a plus rien dans la matrice. Bye !\n") rep <- "NO" } # fin si 3. Déboggage Ce que nous venons de faire est un peu du "bricolage" : pour trouver ce qui ne va pas, nous avons ajouté des print() et nous avons réexécuté le programme. R dispose d'outils beaucoup plus professionnels pour suivre le comportement des fonctions. La première fonction utile à ce sujet est sans doute browser() -- à ne pas confondre avec la fonction browseURL() qui affiche une URL dans le navigateur. Mettre browser() dans le corps d'une fonction permet d'interrompre momentanément l'exécution de la fonction en cours tout en ayant accès à R . On peut donc taper des commandes, interroger les variables ou les modifier... Lorsque R exécute browser(), le prompt est modifié et affiche Browse[n]. Différentes commandes sont ajoutées à l'environnement habituel de R. Ainsi n exécute juste une instruction, c quitte ce browser et reprend l'exécution de la fonction en cours à l'instruction suivante dans la fonction, f permet de terminer la boucle courante ou la fonction, Q quitte le browser et la fonction. Pour éviter d'avoir à ajouter browser() dans le code puis de l'enlever quand tout va bien -- il est sans doute plus prudent de le mettre en commentaire et de le décommenter pour le réutiliser au prochain "bug" -- R fournit les fonctions debug() et undebug. Ecrire debug(f) exécute systématiquement browser() dès que la fonction f est appelée. undebug(f) vient annuler ce comportement. On peut se dispenser d'exécuter undebug(f) si la fonction f est redéfinie, par exemple si on lit son code dans un fichier... Pour bien comprendre comment tout cela fonctionne, supposons que la boucle "TANT QUE" de notre exemple précédent soit dans la fonction gereMatrice, la matrice étant passée en paramètre. Voici donc le code à dépanner : # un comportement bizarre de R gereMatrice <- function(mat,rep="OK") { # affichage initial cat("\nVoici la matrice au départ,\n") cat("avec",nrow(mat),"lignes et",ncol(mat),"colonnes\n") print(mat) # suppression interactive de ligne ou de colonne rep <- "OK" while (rep=="OK") { # même code qu'au début du chapitre } # fin tant que } # fin de fonction gereMatrice L'encadré suivant montre un exemple de session interactive qui permet de suivre ce que fait R au niveau du déboggage (nous avons juste aménagé un peu le texte). On commence par indiquer à R qu'on veut débugger notre fonction : > debug(gereMatrice) > gereMatrice( matrix(1:4,nrow=2) ) debugging in: gereMatrice(matrix(1:4, nrow = 2)) debug à bizar15.r#3 :{ [...] ### gh ### R affiche tout le code de fonction Browse[2]> On utilise ensuite n pour avancer dans l'exécution de la fonction. R affiche chaque instruction avant de l'exécuter. Ici, nous avons appuyé 5 fois sur n, pour arriver à l'intérieur de la boucle : Browse[2]> n debug à bizar15.r#7 :cat("\nVoici la matrice au départ,\n") Browse[2]> n Voici la matrice au départ, debug à bizar15.r#8 :cat("avec", nrow(mat), "lignes et", ncol(mat), "colonnes\n") Browse[2]> n avec 2 lignes et 2 colonnes debug à bizar15.r#9 :print(mat) Browse[2]> n [,1] [,2] [1,] 1 3 [2,] 2 4 debug à bizar15.r#13 :rep <- "OK" Browse[2]> n debug à bizar15.r#14 :while (rep == "OK") { [...] ### gh ### R affiche tout le code de la boucle Browse[2]> Nous continuons l'exécution de la fonction avec des n successifs, pour arriver juste avant l'exécution du code qui supprime une ligne ou une colonne : Browse[2]> n debug à bizar15.r#16 :cat(" taper L pour supprimer une ligne, ") Browse[2]> n taper L pour supprimer une ligne, debug à bizar15.r#17 :cat(" ou C pour supprimer une colonne, ") Browse[2]> n ou C pour supprimer une colonne, debug à bizar15.r#18 :nature <- readline() Browse[2]> n L debug à bizar15.r#19 :objet <- ifelse(nature == "L", "ligne", "colonne") Browse[2]> n debug à bizar15.r#21 :cat(" en quelle position ? ") Browse[2]> n en quelle position ? debug à bizar15.r#22 :position <- as.numeric(readline()) Browse[2]> n 1 debug à bizar15.r#24 :if (objet == "ligne") { mat <- mat[-position, ] } else { mat <- mat[, -position] } Browse[2]> Maintenant, interrogeons nos divers objets, exécutons la suppression et regardons la classe et le contenu de la matrice : Browse[2]> objet [1] "ligne" Browse[2]> nature [1] "L" Browse[2]> class(mat) [1] "matrix" Browse[2]> n debug à bizar15.r#25 :mat <- mat[-position, ] Browse[2]> n debug à bizar15.r#30 :cat("Après suppression de la ", objet, "numéro", position, "\n") Browse[2]> class(mat) [1] "integer" Browse[2]> mat [1] 2 4 C'est fini, nous avons bien localisé l'endroit où R change la matrice. Il reste à taper Q puis undebug(gereMatrice) pour revenir à un comportement "normal" de R : Browse[2]> Q > undebug(gereMatrice) Il ne faut pas hésiter à recourir à la fonction debug() car c'est un outil très pratique qui permet de localiser les erreurs. De plus, Rstudio fournit un environnement adapté à debug() avec des boutons pour les actions c, n... et le panneau de droite montre les variables locales... A l'usage, c'est beaucoup plus complet et beaucoup plus pratique que le mode session de l'interface standard de R. 4. Ecrire <<- n'est pas une faute de frappe Il arrive parfois les programmes soient longs à s'exécuter et nous essaierons de gérer ce problème dans la section suivante. Il arrive aussi qu'un programme s'exécute sans erreur apparente mais avec un résultat faux au bout du compte. Pour peu qu'il y ait beaucoup de résultats intermédiaires, ou beaucoup de variables et beaucoup de fonctions, la technique précédente avec debug() et browser est parfois un peu "lourde" à utiliser, en particulier parce qu'il s'agit d'un environnement local. Une fois debug() quitté, les variables locales utilisées par la fonction ont disparu. R fournit avec l'instruction <<- un moyen intéressant de "sauvegarder" des variables. Mais commençons par regarder cette disparition des variables. Par défaut, toute variable dans une fonction est locale, ce qu'on peut voir avec le code suivant pblv <- "non !" # pblv : Plus Belle La Vie pourLesVieux <- function() { pblv <- "OUI" cat(" en local : ",pblv,"\n") } # fin de fonction pourLesVieux cat("global : ",pblv,"\n") pourLesVieux() cat("global : ",pblv,"\n") dont l'exécution fournit : global : non ! en local : OUI global : non ! Une fonction l'exécution terminée, on n'a plus accès aux variables définies dans la fonction. Si on écrit <<- au lieu de <-, R vient écrire la variable dans l'environnement parent donc pour nous ici dans l'environnement global. Ainsi avec pblv <- "non !" # pblv : Plus Belle La Vie pourLesVieux <- function() { pblv <<- "OUI" # AVEC DEUX SYMBOLES < cat(" en local : ",pblv,"\n") } # fin de fonction pourLesVieux cat("global : ",pblv,"\n") pourLesVieux() cat("global : ",pblv,"\n") on obtient : global : non ! en local : OUI global : OUI Il est clair que pour notre exemple, cela ne sert pas à grand-chose. Pour un exemple en vraie grandeur, utiliser <<- dans le corps de la fonction, ou même à l'intérieur de debug() peut permettre de sauvegarder les "grosses" variables (listes nommées, data frame construits progressivement...) dans différents états au cours de l'exécution afin de pouvoir comparer après coup les structures, ou même simplement pour documenter ce qui se passe en début, en cours et en fin d'exécution... 5. Profilage Une fois que les programmes sont justes et qu'il s'exécutent "bien", on peut vouloir qu'ils s'exécutent "vite". Mais d'où vient la lenteur de notre code ? Imaginons qu'on ait deux fonctions appelées à l'intérieur d'un programme. La lenteur vient peut-être de la première fonction, ou de la deuxième ou peut-être même des autres parties du programme. Pour tester cela, R fournit en standard plusieurs fonctions, dont Rprof() et summaryRprof(). Voici comment les utiliser : on lance Rprof(), on exécute le code et ensuite on demande à R via summaryRprof() d'afficher les résultats du profilage. Imaginons par exemple qu'une fonction h() appelle la fonction f() et la fonction g(), comme dans le code du fichier lent01.r suivant f <- function(x,n) { for (nbfois in 1:n) { x <- c(x,nbfois) } # fin pour return(x) } # fin de fonction f g <- function(x,n) { for (nbfois in 1:n) { x <- x + 1 } # fin pour return(x) } # fin de fonction g h <- function(n) { x <- 0 x <- f(x,n) y <- 1 y <- g(y,n) } # fin de fonction h h(5*10**4) Voici le code à utiliser pour analyser notre fonction h() Rprof() source("lent01.r",encoding="latin1") Rprof(NULL) summaryRprof() Et son résultat sachant que les durées sont exprimées en secondes : > summaryRprof() $by.self self.time self.pct total.time total.pct "c" 5.00 98.43 5.00 98.43 "f" 0.06 1.18 5.06 99.61 "+" 0.02 0.39 0.02 0.39 $by.total total.time total.pct self.time self.pct "eval" 5.08 100.00 0.00 0.00 "h" 5.08 100.00 0.00 0.00 "source" 5.08 100.00 0.00 0.00 "withVisible" 5.08 100.00 0.00 0.00 "f" 5.06 99.61 0.06 1.18 "c" 5.00 98.43 5.00 98.43 "+" 0.02 0.39 0.02 0.39 "g" 0.02 0.39 0.00 0.00 $sample.interval [1] 0.02 $sampling.time [1] 5.08 Les quatre dernières lignes de l'affichage de $by.total montrent clairement que les fonctions f() et c() prennent beaucoup plus de temps à s'exécuter que les fonctions +() et g(). Pour tester plus finement du code, on peut utiliser le package nommé microbenchmark. Par exemple, est-il plus rapide de générer un vecteur de valeurs numériques suivant une loi uniforme ou une loi normale ? Voici le code qui donne la réponse (il est plus lent de générer des données normales), avec son exécution : > library("microbenchmark") > n <- 3*10**5 > microbenchmark( a <- runif(n), b <- rnorm(n) ) Unit: milliseconds expr min lq mean median uq max neval a <- runif(n) 10.31694 10.32199 12.16642 10.32667 10.98350 59.37682 100 b <- rnorm(n) 25.70522 25.75042 27.25000 25.77834 27.35857 75.23661 100 De même, nous avions écrit qu'il vaut mieux éviter de réaliser le même appel de fonction si les paramètres ne changent pas. Voici un exemple chronométré de ce que cela signifie. Soit le code R suivant à évaluer : library("microbenchmark") f <- function(v) { return(list( sum(v==max(v)),which(v==max(v)) )) } # fin de fonction f g <- function(v) { maxv <- max(v) return(list( sum(v==maxv), which(v==maxv) )) } # fin de fonction g microbenchmark( v <- runif(10**6), f(v) , g(v) ) # fin de microbenchmark Pour comprendre qu'il ne s'agit que d'une évaluation du temps passé, voici deux exécutions de ce programme : Unit: milliseconds expr min lq mean median uq max neval cld v <- runif(10^6) 34.39743 34.46519 40.33607 35.65167 36.15951 86.18001 100 c f(v) 22.91168 24.65615 31.64044 24.83843 25.94697 73.81922 100 b g(v) 19.31882 21.02488 26.43521 21.07547 22.05723 70.80157 100 a Unit: milliseconds expr min lq mean median uq max neval cld v <- runif(10^6) 34.39903 35.06691 40.89298 36.01946 36.19025 85.32907 100 b f(v) 22.92871 24.63554 30.57184 24.69739 25.35163 74.58290 100 a g(v) 19.32942 21.01391 25.81828 21.06611 21.47420 71.03639 100 a A la lecture de ces résultats, la fonction f est bien plus lente que la fonction g : il ne faut donc pas calculer plusieurs fois max(v) mais bien mettre cette valeur dans une variable comme maxv. On peut aussi vouloir s'intéresser non pas aux fonctions mais aux lignes de code. Le package lineprof permet un tel profilage et fournit un affichage adapté. Attention : ce package n'est pas disponible directement via le CRAN mais via github seulement. Il utilise le package shiny pour un affichage interactif dans le navigateur. Pour installer ce package lineprof, il faut écrire (sous réserve, donc, que le package devtools soit installé au préalable) : devtools::install_github("hadley/lineprof") Admettons par exemple que l'on veuille analyser les lignes du code suivant : lent <- function() { print(date()) n <- 8*10**4 x <- c() y <- 0 for (i in (1:n)) { x <- c(x,i) y <- y + 1 } # fin pour i print(date()) } # fin de fonction lent Pour cela, on écrit library(lineprof) # chargement profil <- lineprof( lent() ) # exécution shine( profil ) # visualisation Et on obtient dans le navigateur par défaut : 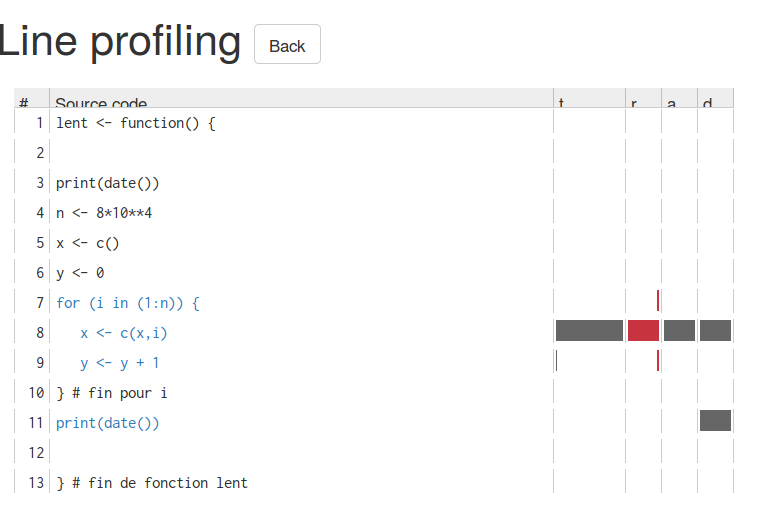Il est facile de voir que la ligne 8 est la plus "consommatrice". 6. Optimisation Maintenant que nous savons quelle partie de code est lente, comment aller plus vite ? C'est une question compliquée car il est possible que la méthode soit lente : si vous avez décidé, par exemple, de passer en revue toutes les sous-chaines de caractères d'un génome humain, ce sera forcément assez long, disons plusieurs dizaines de minutes sans doute. Donc nous allons supposer que le code est "bon" mais lent. Une fois repérées les parties vraiment lentes grâce à la section précédente, il faut essayer d'appliquer quelques grands principes pour éviter qu'un code ne soit lent. Si ce n'est pas suffisant, il faudra analyser si la lenteur vient du langage, en interne, ou si cela vient de notre façon de coder. Tout d'abord, comme nous venons de le voir, un premier grand principe est qu'il ne faut pas effectuer deux fois le même calcul déterministe sur une structure si elle ne change pas. Donc si on utilise une boucle POUR, par exemple, il faut enlever tous les calculs comme 3*h si h ne dépend pas de l'indice de boucle... Ensuite, il faut essayer d'utiliser les fonctions vectorielles de R plutôt que de réécrire soi-même les calculs. Voici par exemple pourquoi il ne faut pas réinventer la somme d'un vecteur : somme1 <- function(v) { return( sum(v) ) } # fin de fonction somme1 somme2 <- function(v) { somme <- 0 for (element in v) { somme <- somme + element } # fin pour element return( somme ) } # fin de fonction somme2 microbenchmark( somme1(10**6), somme2(10**6) ) # fin de microbenchmark Unit: microseconds expr min lq mean median uq max neval cld somme1(10^6) 1.142 1.2790 1.93744 1.5270 1.6440 23.361 100 a somme2(10^6) 1.313 1.5805 2.14648 1.7725 1.8815 20.343 100 a Un deuxième grand principe est qu'il ne faut pas laisser R gérer la mémoire. Malheureusement, ce n'est pas toujours facile de savoir quand R recopie les variables en mémoire. Disons, pour simplifier, qu'il est prudent de prévoir au maximum les tailles des tableaux résultats, de les initialiser et ensuite de les remplir. Imaginons par exemple que l'on veuille calculer n nombres "simples", par exemple tous les nombres de 1 à n. Si vous écrivez cela en concaténant chaque nouveau nombre au vecteur précédent des résultats, soit le code remplissage1 <- function( nbValeurs=8*10**4 ) { vecRes <- c() # vecteur des résultats for (ind in (1:nbValeurs)) { vecRes <- c(vecRes,ind) } # fin pour ind return( vecRes ) } # fin de fonction remplissage1 alors R viendra de temps en temps ou peut-être même à chaque fois recopier le vecteur v en mémoire. Il est beaucoup plus efficace de prévoir un vecteur de la "bonne taille" (voir l'exercice 3 associé à cette page qui explicite les stratégies possibles lorsqu'il n'est pas possible de prévoir avant l'exécution la taille des résultats) et de le remplir au fur et à mesure, soit le code : remplissage2 <- function( nbValeurs=8*10**4 ) { # initialisation du vecteur des résultats avec la bonne taille vecRes <- rep(0,nbValeurs) # remplissage for (ind in (1:nbValeurs)) { vecRes[ind] <- ind } # fin pour ind return(vecRes) } # fin de fonction remplissage2 Mais de toutes façons ce ne sera jamais aussi efficace que le code R natif et vectoriel : remplissage3 <- function( nbValeurs=8*10**4 ) { vecRes <- 1:nbValeurs return( vecRes ) } # fin de fonction remplissage3 En voici la preuve, avec une machine qui a beaucoup de mémoire. Nous avons pris la précaution de vérifier que l'ordre des instructions ne perturbe pas les résultats (à cause des encombrements mémoire successifs) : > library("microbenchmark") > n <- 10**4 > microbenchmark( a <- remplissage1(n), b <- remplissage2(n), c <- remplissage3(n) ) # fin de microbenchmark Unit: microseconds expr min lq mean median uq max neval cld a <- remplissage1(n) 98655.609 101171.269 104653.99511 102550.045 103735.207 143625.852 100 c b <- remplissage2(n) 6794.431 7388.097 8092.45409 7584.002 8710.362 11176.973 100 b c <- remplissage3(n) 5.004 6.139 8.82518 9.639 10.759 14.907 100 a > microbenchmark( c <- remplissage3(n), a <- remplissage1(n), b <- remplissage2(n) ) # fin de microbenchmark Unit: microseconds expr min lq mean median uq max neval cld c <- remplissage3(n) 4.952 6.2715 9.05478 9.7185 10.7445 20.37 100 a a <- remplissage1(n) 101334.792 103374.7525 107689.51062 104629.8870 106394.4925 150000.07 100 c b <- remplissage2(n) 6680.088 7267.6015 7902.64836 7575.8575 8368.8110 11169.16 100 b   Partie 9 - Différences entre programmation et développement   Table des matières cliquable   1. Programmation, choix, tests, déboggage et profilage   2. Programmation, spécifications et documentations   3. Mises à jour, maintenances, objets et packages   4. Programmation et Interfaçage   5. Conclusion 1. Programmation, choix, tests, déboggage et profilage Programmer, c'est écrire des programmes. Soit. Mais comment être sûr que les programmes sont justes ? Et que les autres sauront les utiliser ? Après réflexion, ce n'est pas si simple... Prenons un exemple concret, celui de la conversion de et vers des pouces en cm : une fois que l'on sait qu'un pouce fait 2,54 cm, tout n'est pas dit. Ainsi, comment entrer les valeurs et l'unité ? Faut-il écrire une fonction qui pose une question, lit la réponse au clavier en session R, ou passer ces valeurs en paramètres, ou utiliser un formulaire Tcl/Tk, voire une interface Web ? Admettons un instant que l'on s'en tienne au premier choix, à savoir la lecture au clavier -- ce qui sans doute pas une bonne solution, ce que l'on verra plus loin. Voici un exemple de programme. Voyez-vous l'erreur de programmation ? ########################################### # # conversion pouce/cm # # (avec une erreur facile à éviter) # ########################################### # on pose la question 1 et on lit la réponse valeur <- as.numeric(readline(prompt="quelle quantité voulez-vous convertir ? ")) # on pose la question 2 et on lit la réponse unite <- readline(prompt="en quelle unité ? ") # on convertit : si pouce on multiplie, sinon on divise facteurConv <- 2.54 if (unite=="pouces") { autreu <- "cm" ; } else { facteurConv <- 1/facteurConv ; autreu <- "pouces" ; } ; # fin si cat(valeur," ",unite," = ",(valeur*facteurConv)," ",autreu,".\n",sep="") ; Une lecture rapide du programme et le test avec un cas "idéal" comme ci-dessous : quelle quantité voulez-vous convertir ? 10 en quelle unité ? pouces 10 pouces = 25.4 cm. ne permet pas de prouver que le programme est juste. Cela montre seulement que si on fournit les bons paramètres (en type et en valeur), le calcul est correct. Oui mais, si on saisit pouce au lieu de pouces, c'est-à-dire sans le s à la fin, que fait le programme ? Stricto sensu, pouce et pouces ne sont pas égaux donc le programme fait la conversion dans le mauvais sens. Une version plus fiable serait donc ########################################### # # conversion pouce/cm # ########################################### # on pose la question 1 et on lit la réponse valeur <- as.numeric(readline(prompt="quelle quantité voulez-vous convertir ? ")) # on pose la question 2 et on lit la réponse unite <- readline(prompt="en quelle unité ? ") # on convertit : si pouce on multiplie, sinon on divise facteurConv <- 2.54 uniteOk <- 0 if (unite=="pouces") { autreu <- "cm" ; uniteOk <- 1 } ; if (unite=="cm") { facteurConv <- 1/facteurConv ; autreu <- "pouces" ; uniteOk <- 1 } ; # fin si if (uniteOk==0) { cat(" unité incorrecte. il faut écrire exactement \"pouces\" ou \"cm\" comme unité.\n") } else { cat(valeur," ",unite," = ",(valeur*facteurConv)," ",autreu,".\n",sep="") ; } # finsi Maintenant, pourquoi ne tester que l'unité ? Avec un utilisateur pressé, ou le clavier numérique désactivé, la saisie de la valeur peut être vide. Dans ce cas, la variable valeur contient NA car la fonction as.numeric() ne renvoie pas d'erreur. Ecrire un programme juste, c'est à la fois penser aux erreurs possibles, les détecter et les gérer. On peut décider de boucler sur la saisie d'une valeur numérique ou quitter le programme dès la première saisie si la valeur n'est pas numérique... Programmer, c'est donc faire des choix. Programmer, c'est aussi tester les divers cas possibles que l'on a recensé. C'est pourquoi la saisie au clavier est une mauvaise solution. Car il faudra taper les réponses à chaque fois que l'on veut vérifier que ce qu'on a écrit est correct. Une solution plus "propre" et qui correspond plus à l'esprit de R est de définir une fonction de conversion avec les deux paramètres : convPouceCm <- function(valeur,unite) { ########################################### # # conversion pouce/cm # ########################################### if (missing(valeur) | missing(unite)) { cat("\n") cat(" syntaxe : convPouceCm(valeur,unite) avec unite = pouces ou cm\n") cat(" exemples : convPouceCm(10,\"pouces\")\n") cat(" convPouceCm(20,\"cm\")\n\n") stop() } ; # finsi # pouce on multiplie, sinon on divise facteurConv <- 2.54 uniteOk <- 0 if (unite=="pouces") { autreu <- "cm" ; uniteOk <- 1 } ; if (unite=="cm") { facteurConv <- 1/facteurConv ; autreu <- "pouces" ; uniteOk <- 1 } ; # fin si if (uniteOk==0) { cat(" unité incorrecte. il faut écrire exactement \"pouces\" ou \"cm\" comme unité.\n") } else { cat(valeur," ",unite," = ",(valeur*facteurConv)," ",autreu,".\n",sep="") ; } # finsi } # fin de fonction convPouceCm L'intérêt, c'est que maintenant on peut demander à R de tester les cas possibles juste en éxécutant le script suivant : ############################################## # # test de la fonction de conversion pouce/cm # nommée convPouceCm # ############################################# cat("# test 1 : rappel de la syntaxe si aucune valeur\n") try( convPouceCm() ) cat("# test 2 : calcul correct pour des pouces\n") convPouceCm(10,"pouces") cat("# test 3 : calcul correct pour des centimètres\n") convPouceCm(20,"cm") cat("# test 4 : comportement de la fonction si unité incorrecte...\n") convPouceCm(20,"pommes") Voici ce qu'on obtient alors : # test 1 : rappel de la syntaxe si aucune valeur syntaxe : convPouceCm(valeur,unite) avec unite = pouces ou cm exemples : convPouceCm(10,"pouces") convPouceCm(20,"cm") Error in convPouceCm() : # test 2 : calcul correct pour des pouces 10 pouces = 25.4 cm. # test 3 : calcul correct pour des centimètres 20 cm = 7.874016 pouces. # test 4 : comportement de la fonction si unité incorrecte... unité incorrecte. il faut écrire exactement "pouces" ou "cm" comme unité. Si on veut vraiment saisir les informations au clavier, on écrira une autre fonction par exemple, saisieConversion() qui renvoie les deux valeurs. Du coup, on peut écrire convPouceCm( saisieConversion() ) pour exécuter les deux actions  # fonction de saisie pour conversion pouce/cm saisieConversion <- function() { # on pose la question 1 et on lit la réponse valeur <- as.numeric(readline(prompt="quelle quantité voulez-vous convertir ? ")) # on pose la question 2 et on lit la réponse unite <- readline(prompt="en quelle unité ? ") # on renvoie les deux valeurs return( c(valeur,unite)) } # fin de fonction saisieConversion ######################################################### convPouceCm <- function(valeur,unite) { ########################################### # # conversion pouce/cm # ########################################### if (length(valeur)==2) { # données issues de saisieConversion unite <- valeur[2] # dans cet ordre ! valeur <- as.numeric(valeur[1]) } # finsi if (missing(valeur) | missing(unite)) { cat("\n") cat(" syntaxe : convPouceCm(valeur,unite) avec unite = pouces ou cm\n") cat(" exemples : convPouceCm(10,\"pouces\")\n") cat(" convPouceCm(20,\"cm\")\n\n") stop() } ; # finsi # pouce on multiplie, sinon on divise facteurConv <- 2.54 uniteOk <- 0 if (unite=="pouces") { autreUnite <- "cm" ; uniteOk <- 1 } ; if (unite=="cm") { facteurConv <- 1/facteurConv ; autreUnite <- "pouces" ; uniteOk <- 1 } ; # fin si if (uniteOk==0) { cat(" unité incorrecte. il faut écrire exactement \"pouces\" ou \"cm\" comme unité.\n") } else { resultat <- valeur*facteurConv cat(valeur," ",unite," = ",resultat," ",autreUnite,".\n",sep="") ; } # finsi return(invisible(c(resultat,autreUnite))) } # fin de fonction convPouceCm Au passage, on pourrait améliorer la fonction convPouceCm() en prévoyant une unité par défaut, un affichage par défaut avec deux décimales, le choix de l'affichage ou non, le renvoi du résultat, ce qui permettrait de tester le programme avec lui-même : > cnv <- convPouceCm( saisieConversion() ) quelle quantité voulez-vous convertir ? 10 en quelle unité ? pouces 10 pouces = 25.4 cm. > cnv <- convPouceCm( cnv ) 25.4 cm = 10 pouces. > cnv <- convPouceCm( cnv ) 10 pouces = 25.4 cm. Lorsque le programme écrit est d'importance, il est essentiel de pouvoir vérifier chaque calcul intermédiaire, de pouvoir suivre le détail à l'intérieur de chaque boucle, ou au contraire, de pouvoir tout exécuter jusqu'à une partie délicate. De même, si la vitesse d'exécution du programme est mauvaise, il faut pouvoir analyser le comportement du programme, savoir où R «perd du temps», ce qui le ralentit... R et Rstudio disposent de fonctions pour cela, heureusement. 2. Programmation, spécifications et documentations Ce que montre la section précédente, c'est qu'il faut bien détailler ce que l'on veut faire, bien préciser les entrées, les sorties. Autoriser p ou i ou d comme abbréviation [internationale] légale de pouces est sans doute une bonne idée car on dit inch en anglais et Daumen en allemand. Fournir le code-source de la conversion ou le rendre accessible sur Internet c'est offrir la possibilité aux autres de le lire et peut-être vous aider à l'améliorer (il vaut mieux alors mettre les commentaires en anglais, malheureusement). Si on n'écrit pas une fonction mais un ensemble de fonctions, il est conseillé de fournir des exemples d'utilisation, un petit manuel pour rappeler les options, détailler le format des structures utilisées. Si cela met en jeu des fichiers de données, il est d'usage de fournir des exemples de tels fichiers, pour qu'une personne qui n'a pas écrit ces fonctions arrive à les utiliser et à comprendre comment elles fonctionnent juste à la lecture de l'aide. Si c'est encore plus complexe, il faut carrément écrire un livre pour expliquer tout cela en détail, comme par exemple avec ces deux ouvrages : Paradis Hahne 3. Mises à jour, maintenances, objets et packages Il est fréquent qu'on ne pense pas tout de suite à tout, qu'on vienne ajouter des fonctionnalités au fur et à mesure de l'utilisation des programmes. C'est pourquoi il est important de bien gérer les numéros de version, de noter ce qui change (il faut parfois défaire ce qui a été fait et revenir à une version antérieure). Dans certains cas, notamment quand ce qu'on écrit dépend des packages de R, il faut parfois modifier le code par ce que R a changé ou par ce que le package a changé. Les tests cités dans la section précédente doivent alors permettre de prouver que malgré les changements les programmes font comme avant et même plus qu'avant. La rétrocompatibilité et la fiabilité sont des concepts à retenir et à implémenter. La maintenance du code peut parfois se limiter à la traduction des messages dans différentes langues, à ajouter des paramètres, mais elle peut parfois être beaucoup plus lourde, par exemple quand on vient factoriser du code, c'est-à-dire mettre des parties en commun via des sous-programmes qui couvrent plusieurs cas. Ces quelques séances d'initiation à la programmation élementaire ne peuvent pas, bien sûr, présenter des concepts plus techniques comme les objets et l'écriture de packages. Nous renvoyons pour cela aux exercices de cettes section afin d'avoir une petite idée de ce que cela met en jeu. 4. Programmation et Interfaçage La notion d'interface correspond à deux choses bien distinctes : les interfaces utilisateurs et les interfaces de programmation. Dans le premier cas, il s'agit de savoir comment l'utilisateur interagit avec les fonctions et les programmes (en ligne de commande, par script, par menus, par panneaux...). Dans le second cas, il s'agit de faire dialoguer entre eux les langages, d'appeler du C via R, par exemple, ou de demander à Python ou Ruby d'exécuter du R. On pourra consulter les liens ci-dessous pour voir des exemples possibles d'interface de programmation.           Rcpp          R py2          R in Ruby Au niveau des interfaces utilisateur, à part des interfaces générales avec menus comme Rkward et Rcmdr, R fournit un package nommé tcltk qui permet de développer des GUI et un package nommé shiny pour définir des interfaces web. Ainsi le code suivant   # saisie de valeur et unite en mode interface graphique library(tcltk2) tt <- tktoplevel() tktitle(tt) <- "Saisie des paramètres pour conversion" l1 <- tklabel(tt,text="quelle quantité voulez-vous convertir ?") v1 <- tclVar(10) e1 <- tkentry(tt,textvariable=v1) l2 <- tklabel(tt,text="en quelle unité ? ") v2 <- tclVar("pouces") e2 <- tkentry(tt,textvariable=v2) ok <- tkbutton(tt,text="OK",command = function() tkdestroy(tt)) tkpack(l1,e1,l2,e2,ok) tkwait.window(tt) cat("Valeurs saisies :\n") valeur <- as.numeric( tclvalue(v1) ) unite <- tclvalue(v2) cat(" valeur = ",valeur," et unité = ",unite,"\n") # appel de la fonction de conversion convPouceCm(valeur,unite) fournit une interface graphique minimale (et mal présentée) pour la saisie des deux paramètres dans la conversion pouces/cm...            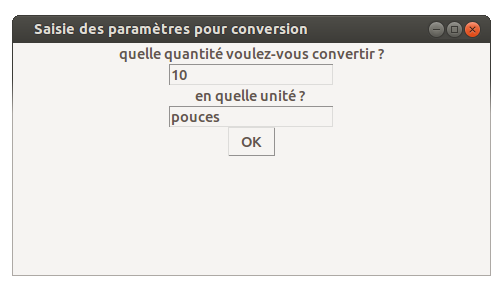Pour shiny, on écrit deux scripts : celui du serveur, nommé server.R et celui de l'interface, nommé ui.R. Voir par exemple la démonstration dans la gallerie de Shiny nommée Iris k-means clustering... 5. Conclusion Les quelques heures passées à écrire des scripts R et à lire les corrigés des exercices vous auront sans doute convaincu(e) que : programmer, c'est assez facile au début, pour des petits calculs ; tout le monde peut programmer, mais bien programmer est un art ; programmer demande de la rigueur, de la constance et de l'endurance ; en d'autres termes, programmer peut se révéler fastidieux et devenir intrinsèquement rébarbatif (pour ne pas dire ch*...) ; programmer demande de la méthode, de la réflexion et du temps ; programmer peut se révéler agréable car cela fait plaisir d'avoir réussi à créer quelque chose qui résoud un problème ou qui fait le travail en automatique à notre place. Alors, un seul mot : tous et toutes à vos papier et crayon avant de passer au clavier !   Code-source php de cette page.

 

 

   Retour à la page principale de   (gH)