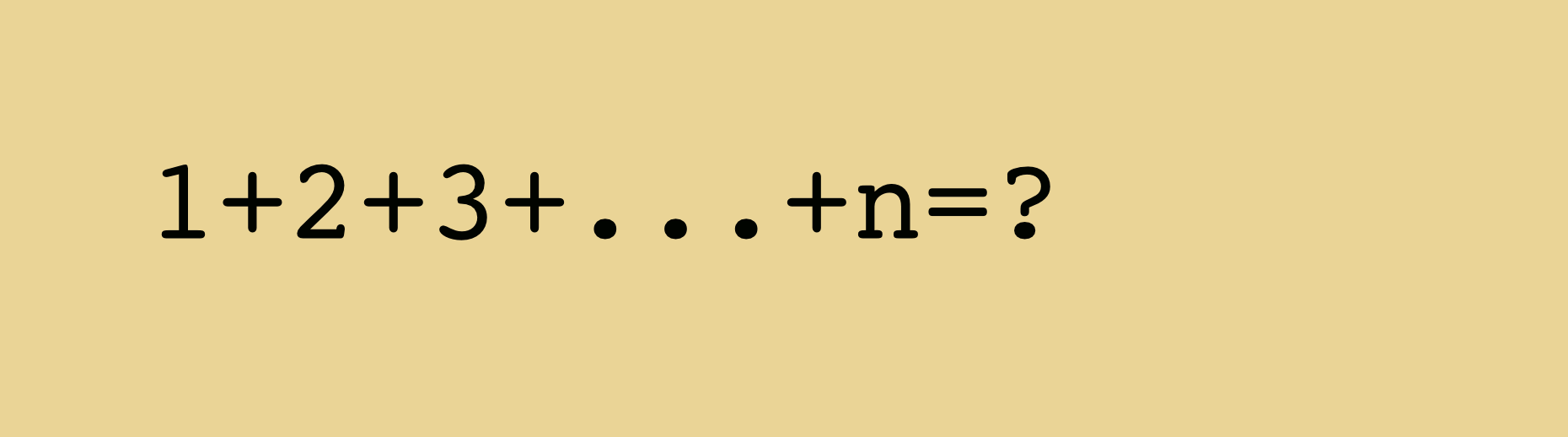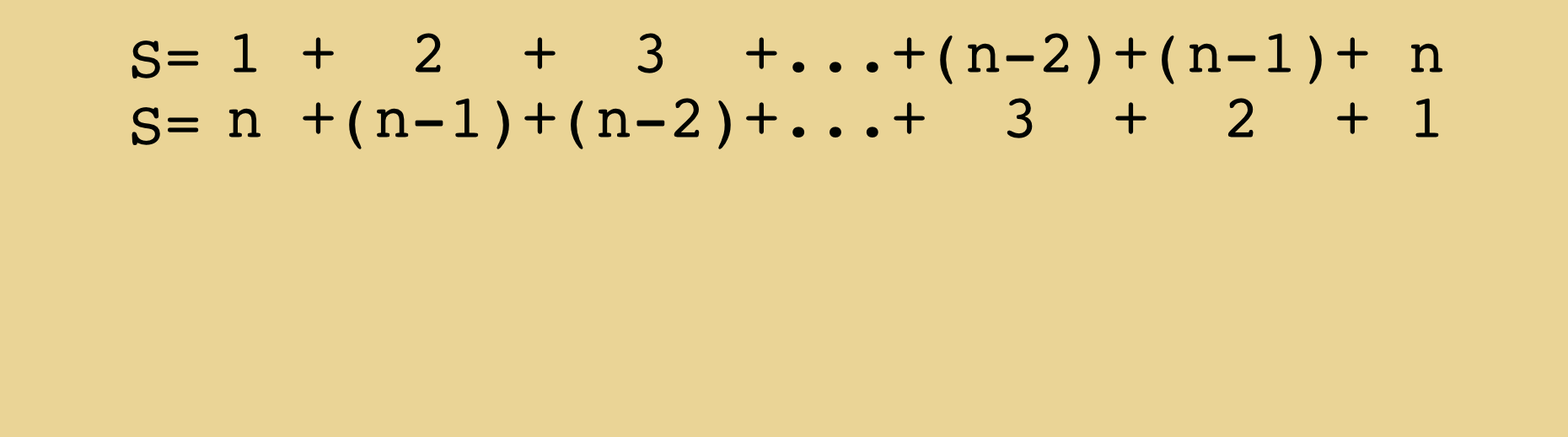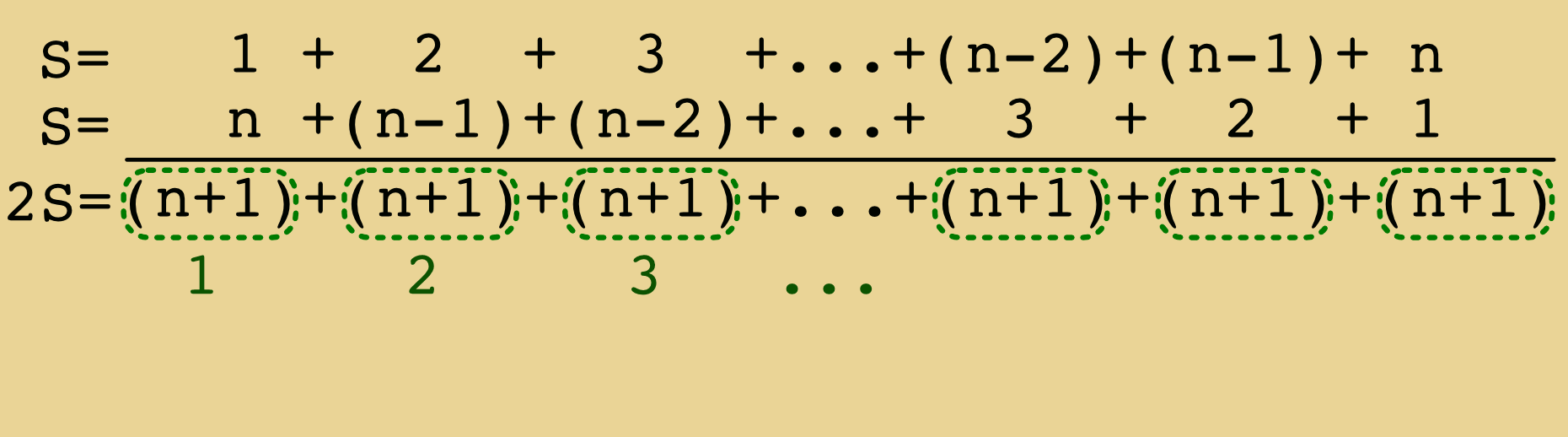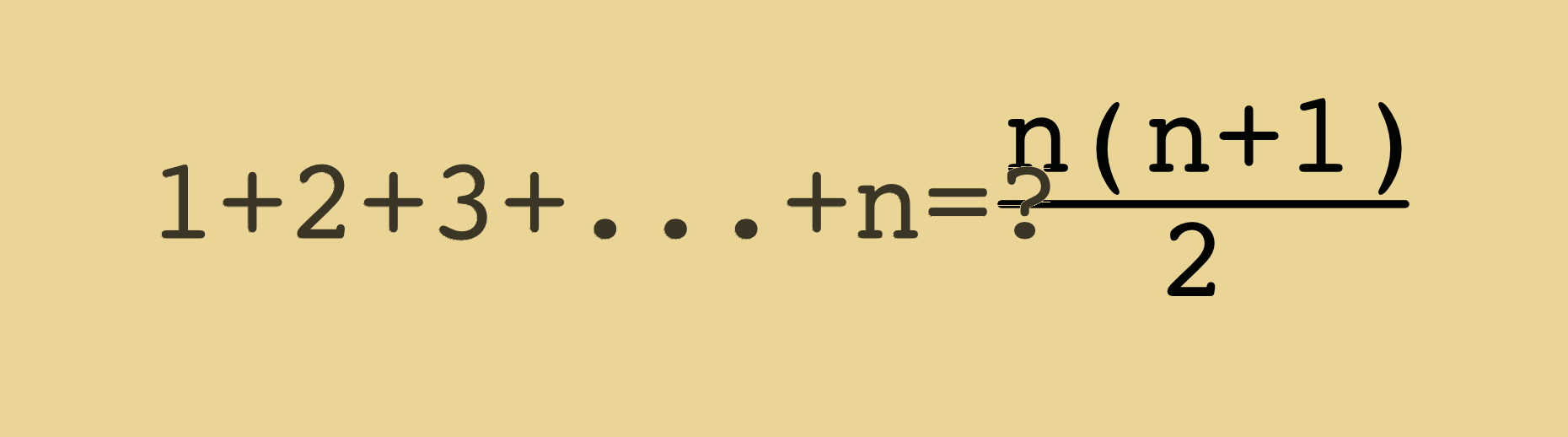Un peu d'arithmétique
Mathématiques CRPE, La Rochelle, 2020
gilles.hunault "at" univ-angers.fr
1. Le vocabulaire du calcul arithmétique
L'arithmétique se préoccupe a priori des nombres entiers (positifs ou négatifs) et de leurs propriétés.
La résolution de l'équation du premier degré $ax+b=0$ pour $a$ et $b$ entiers n'aboutit pas systématiquement à un nombre entier, d'où la notion de divisibilité.
Pour que $p/q$ soit un entier, avec $p$ et $q$ entiers, il faut que $p$ soit un multiple de $q$ ce qui s'écrit $p=k\times q$ .
Si $p=k\times q$ , on dit de façon équivalente que $q$ (et $k$ aussi) est un diviseur de $p$ , que $p$ est divisible par $q$ .
Un nombre qui n'a pas d'autre diviseur que 1 et lui-même se nomme un nombre premier. Tout nombre entier admet une décomposition unique en un produit de puissances de nombres premiers, comme par exemple $123456789 = 3^2 \times 3607 \times 3803$ .
On pourra utiliser le site dnp pour vérifier la décomposition d'un entier en nombres premiers (on dit aussi "en facteurs premiers").
Si deux nombres entiers n'ont pas de diviseur commun autre que 1, on dit qu'ils sont premiers entre eux. Le ppmc de deux nombres entiers est le plus petit multiple commun ; on s'en sert pour trouver le dénominateur commun pour additionner et soustraire les fractions. Le pgdc de deux nombres entiers est le plus grand diviseur commun ; on s'en sert pour simplifier les fractions.
Par exemple, pour calculer $\displaystyle \frac{1}{4} + \frac{3}{10}$ , on cherche le ppmc de $4=2^2$ et de $10=2\times 5$ . On trouve $20=4\times 5=2\times 10$ .
On peut alors additionner les fractions après avoir réduit au même dénominateur qui est donc $20$ :
$\displaystyle \frac{1}{4} + \frac{3}{10}=\frac{1\times 5}{4\times 5}+\frac{~3\times 2}{10\times 2}$ $\displaystyle =\frac{5}{20} + \frac{6}{20}=\frac{5+6}{20}=\frac{11}{20}$ .
Si on utilise la formule non simplifiée d'addition des fractions $\displaystyle \frac{a}{b} + \frac{c}{d}=\frac{a\times d}{b\times d} +\frac{c\times b}{d\times b}$ $\displaystyle =\frac{(a\times d) +(b\times c)}{b\times d}$ ,
il faut calculer le pgcd du numérateur et du dénominateur pour simplifier éventuellement la fraction.
Ainsi, avec le même exemple que précédemment, $\displaystyle \frac{1}{4} + \frac{3}{10}=\frac{(1\times 10)+(4\times 3)}{4\times 10}$ $\displaystyle =\frac{10+12}{40}=\frac{22}{40}$ .
Puisque $22=2\times 11$ et $40=2^2\times 10$ , le pgcd de $22$ et $40$ est 2. D'où :
$\displaystyle \frac{1}{4} + \frac{3}{10}=\frac{22}{40}=\frac{2\times 11}{2\times 20}=\frac{11}{20}$ .
Voici un "truc" pour frimer quand on vous dit que les fractions sont compliquées : si $ a$ est pair et $ b$ impair sans facteur commun avec $ a$ , alors la somme des inverses de $ a$ et de $ b$ est la fraction « somme/produit ». En formule :
$\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{a+b}{a\times b}$ si $ a$ est pair et $ b$ est impair sans facteur commun avec a.
Par exemple :
$\dfrac{1}{2}+\dfrac{1}{3}=\dfrac{2+3}{2\times 3}=\dfrac{5}{6}$
$\dfrac{1}{8}+\dfrac{1}{9}=\dfrac{8+9}{8\times 9}=\dfrac{17}{72}$
La division euclidienne de $a$ par $b$ consiste à trouver $q$ et $r$ tels que $a=b\times q +r$ avec $r<q$ .
Le vocabulaire usuel correspond à l'équation dividende = diviseur $\times$ quotient + reste .
La page Wiki française division euclidienne expose bien ce qu'est cette division et comment elle se réalise informatiquement. A la main, il faut recourir à ce qu'on nomme la division posée pour trouver en plusieurs étapes les valeurs de $b$ , $q$ et $r$ .
La méthode naive de division euclidienne consiste à soustraire $b$ de $a$ et à recommencer jusqu'à ce que la différence soit inférieure strictement à $b$ .
On peut donc se contenter de chercher des multiples de $b$ jusqu'à dépasser $a$ .
Par exemple pour trouver la division euclidenne de $a=15$ par $b=6$ , on peut commencer par $15-6=9$ , donc $15=6+9$ et on continue parce que $9>6$ .
Ensuite $9-6=3$ et $3<6$ donc on a fini. Il reste à reporter les différents calculs : $15=6+9=6+(6+3)=6\times 2 + 3$ .
En utilisant les multiples de $6$ : $6\times 1=~6<15$ ; $6\times 2=12<15$ ; $6\times 3=18>15$ . Donc $15=6\times 2 + r$ Puisque $15-12=3$ on déduit que $r=3$ et on peut écrire $15=6\times 2 + 3$ .
Les suites arithmétiques, les suites géométriques et les suites arithmético-géométriques fournissent des moyens simples de construire et de définir par formule des suites de nombres, pas nécessairement entiers, dont les plus célèbres sont bien sûr $1, 2, 3, 4, 5...$ . et $2, 4, 8, 16, 32...$ .
Plus généralement, une suite mathématique relie un terme à son précédent ou ses précédents par une formule ou un procédé calculatoire. Enumérer les premiers termes d'une suite, mathématique ou pas, constitue un bon moyen de définir des jeux, des énigmes ou des tests (discutables) de Q.I.
Pour la petite histoire ou pour susciter des vocations, certaines suites numériques sont très simples à énoncer mais leurs propriétés mathématiques ne sont parfois pas encore toutes démontrées. La plus célèbre est sans doute la suite de Syracuse inventée parait-il par les russes pour rendre fous les mathématiciens américains et israéliens...!

Pour celles et ceux intéressé(e)s par l'histoire des mathématiques, et en particulier celle de la division dite « à la française », on pourra consulter la page 0-3 de Jean-Luc BREGEON, auteur par ailleurs d'un très intéressant diaporama intitulé mathématiques et maitrise de la langue.
2. Un peu de pratique du calcul arithmétique
Exemple 1
Trouver la "suite logique" des valeurs $u_1=50,\ u_2=61,\ u_3=72$ . Quelle est la formule de $u_n$ ?
solution
On suppose qu'il s'agit d'une suite arithmétique (donc simplement par ajout de valeurs). Il suffit de calculer les différences successives.
Comme ici $61-50=11=72-61$ le prochain terme est $72+11$ soit $83$ .
Pour des enfants qui ne savent pas bien calculer, on peut remarquer la forme des nombres pour en déduire le suivant :
$50=5$ suivi de $0$ ; $61=6$ suivi de $1$ ; $72=7$ suivi de $2$ . Le prochain nombre est $8$ suivi de $3$ , c'est donc $83$ .
La formule de calcul de $u_n$ est $39+n\times 11$ .
Vérifions : $u_1=50=39+11=39+1\times 11$ ; $u_2=61=39+22=39+2\times 11$ ; $u_3=72=39+33=39+3\times 11$ ; $u_4=83=39+44=39+4\times 11$ . C'est bon !
Exemple 2
Quelle est la "suite logique" des valeurs $v_1=1,\ v_2=2,\ v_3=4,\ v_4=8$ ? Quelle est la formule de $v_n$ ?
solution
On suppose qu'il s'agit d'une suite arithmétique. On calcule donc les différences successives.
Malheureusement, ici on trouve $2-1=1$ ; $4-2=2$ ; $8-4=4$ .
Donc il ne s'agit pas d'une suite arithmétique.
On suppose maintenant qu'il s'agit d'une suite géométrique.
On calcule donc les rapports successifs. Ici, on trouve $2/1=2$ ; $4/2=2$ ; $8/4=2$ .
Il s'agit bien d'une suite géométrique. Le prochain terme est donc $8\times 2=16$ .
La formule de calcul de $v_n$ est $2^{n-1}$ .
Vérifions : $v_1=1=2^0=2^{1-1}$ ; $v_2=2=2^1=2^{2-1}$ ; $v_3=4=2^2=2^{3-1}$ ; $v_4=8=2^3=2^{4-1}$ ; $v_5=16=2^4=2^{5-1}$ . C'est bon !
Exemple 3
Quelle est la "suite logique" des valeurs $w_1=1,\ w_2=2,\ w_3=4,\ w_4=7$ ? Quelle est la formule de $w_n$ ?
solution
Les diférences successives ne sont pas égales et les rapports successifs ne sont pas égaux. Donc ce n'est ni une suite arithmétique ni une suite géométrique.
Par contre, comme les différences successives sont $1,\ 2,\ 3$ , la prochaine différence doit être $4$ . Le prochain terme est donc $7+4$ soit $11$ .
La formule de calcul de $w_n$ est $1+n\times(n-1)/2$ .
Vérifions : $w_1=1+1\times 0/2=1$ ; $w_2=1+2\times(2-1)/2=1+2/2=1+1=2$ ; $w_3=1+3\times(3-1)/2=1+3\times 2/2=1+3=4$ ;
$w_4=1+4\times(4-1)/2=1+4\times 3/2=1+12/2=1+6=7$ ; $w_5=1+5\times(5-1)/2=1+5\times 4/2=1+20/2=1+10=11$ . C'est bon !
3. Démonstrations directes et par récurrence en arithmétique
Une démonstration directe procède par équivalence, donc souvent par calcul en décomposition, factorisation, réduction, etc. alors qu'une démonstration par récurrence demande une technique particulière, puisqu'il faut vérifier une étape initiale et démontrer l'inférence.
Voici par exemple comment démontrer de façon directe que $m=n^2+n$ est toujours un nombre pair : comme $m=n^2+n=n(n+1)$ , si $n$ est pair, disons, $n=2k$ , alors $m=2k(n+1)$ donc $m$ est pair. Si $n$ est impair, alors $n+1$ est pair, disons, $n+1=2p$ , alors $m=n(n+1)=n\times 2p$ donc $m$ est pair. Comme nous avons épuisé tous les cas, pair et impair pour $n$ , la démonstration est terminée.
Efectuons maintenant la démonstration par récurrence en nommant $P(n)$ la propriété $m_n=n^2+n\ est\ pair$ . L'étape initiale est $P(1)$ . Elle est vraie puisque pour $n=1$ , $m_1=1(1+1)=2$ est pair. Supposons maintenant que $P(n)$ est vraie et essayons de montrer que $P(n+1)$ est vraie. Pour cela, on va calculer $m_{n+1}$ à l'aide de $m_n$ : $m_{n+1}=(n+1)(n+2)=(n+1)n + (n+1)2$ soit encore $m_{n+1}=m_n+2(n+1)$ . Comme $2(n+1)$ est clairement un nombre pair, disons $2a$ et $m_n=n(n+1)$ est pair par hypothèse de récurrence, disons $2b$ , alors au final $m_{n+1}=2a+2b=2(a+b)$ est un nombre pair, ce qu'il fallait démontrer.
4. Quelques calculs et démonstrations à réaliser
Problème 1 :
Est-ce que la somme de 3 nombres entiers consécutifs est toujours divisible par 3 ?
Quel adverbe est inutile dans l'énoncé précédent ?
Est-ce que la somme de 4 nombres entiers consécutifs est toujours divisible par 4 ?
solution
Après quelques essais numériques, la réponse est oui pour la somme de trois nombres entiers consécutifs. Pour le démontrer, on nomme $n$ le premier des trois nombres consécutifs. Les deux suivants sont alors $n+1$ et $n+2$ . Leur somme est donc $n + (n+1) + (n+2)=3 n + 3 = 3(n+1)$ qui est un multiple de 3.
Pour la somme de 4 nombres entiers, la réponse est non. Il suffit de calculer la somme $1+2+3+4$ pour le montrer puisqu'un contre-exemple suffit à infirmer un énoncé.
L'adverbe inutile dans le premier énoncé est toujours. Un énoncé mathématique est un fait général, avec des sous-entendus. S'il y avait eu marqué « toute somme de trois entiers consécutifs est divisible par 3 », on n'aurait pas eu à se poser la question.
Problème 2 :
Calculer $S(n)=1+2+3+...+n$ en fonction de $n$ .
solution
Avant de démontrer quoi que ce soit, il est prudent de faire quelques essais : $S(1)=1$ ; $S(2)=3$ ; $S(3)=6$ ; $S(4)=10$ ;
La croissance de la suite semble inférieure à celle d'un carré puisque $3^2=9$ et $4^2=16$ .
Si on postule qu'il y a une formule du premier degré en $n$ , disons $S(n)=a\times n+b$ alors on devrait pouvoir trouver $a$ et $b$ à l'aide de $S(1)$ et de $S(2)$ .
Malheureusement la résolution simultanée des deux équations $S(1)=1=a\times 1+b$ et $S(2)=3=a\times 2+b$ aboutit à $a=2$ et $b=-1$ . Si on reporte dans $S(3)$ on trouve $5$ au lieu de $6$ donc la formule n'est pas du premier degré.
Si on postule qu'il y a une formule du second degré en $n$ , disons $S(n)=a\times n^2+b\times n +c$ alors il va falloir effectuer de nombreux calculs parce qu'on a trois inconnues à déterminer... Les plus courageuses et les plus courageux arriveront alors à la formule $S(n)=n(n+1)/2$ qu'il reste encore à démontrer.
Une façon plus astucieuse, attribuée à C. F. Gauss consiste à additionner $S(n)$ et $S(n)$ écrite à partir de la fin. Voir par exemple le wiki français à ce sujet ici qui inclut la démonstration graphique ci-dessous :
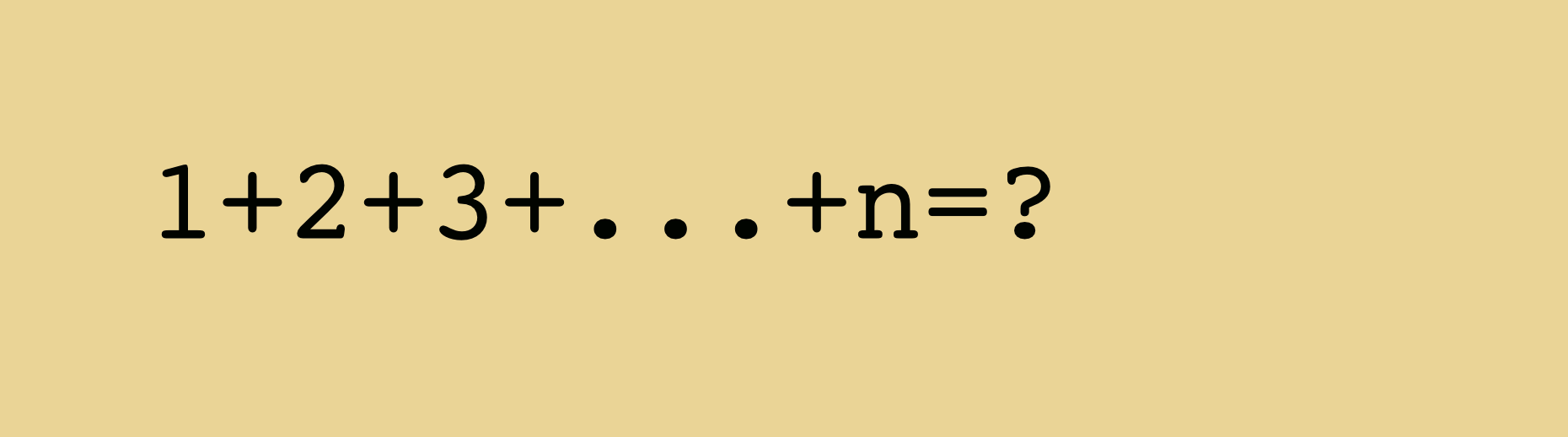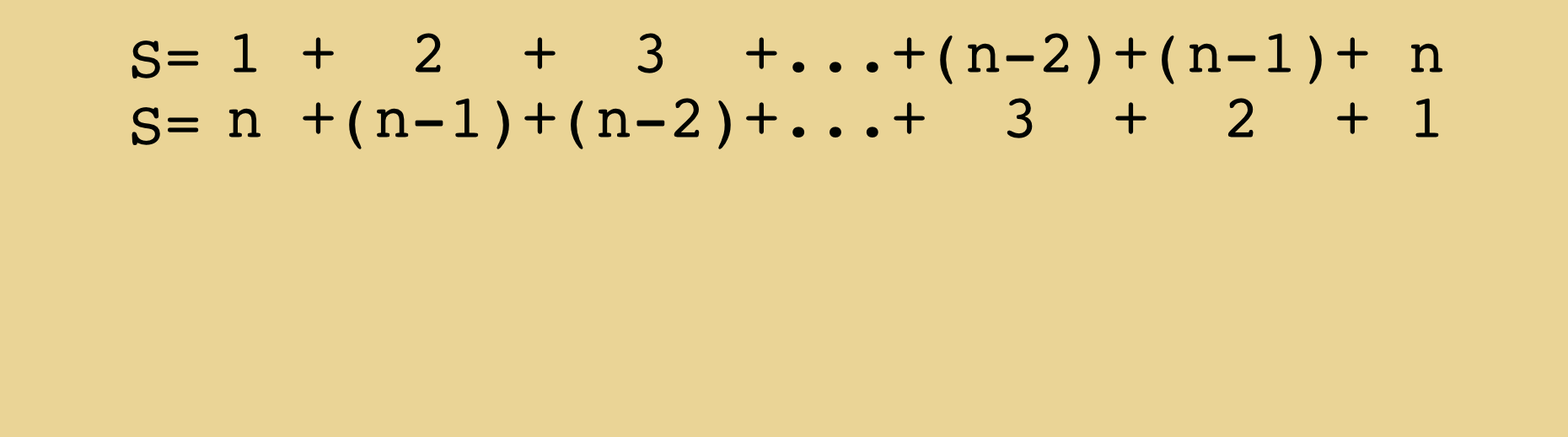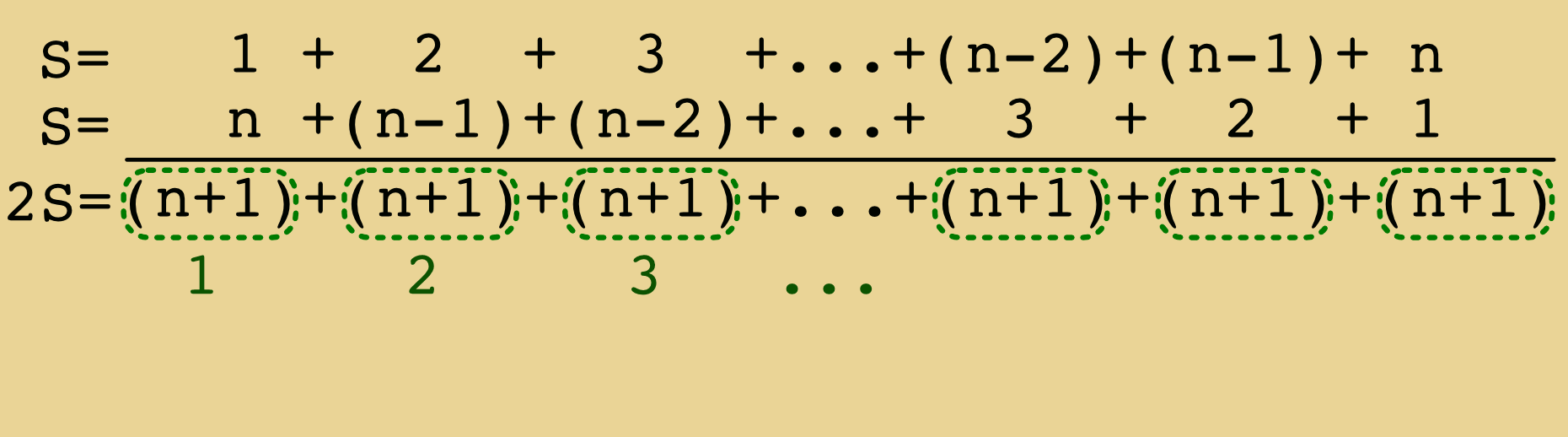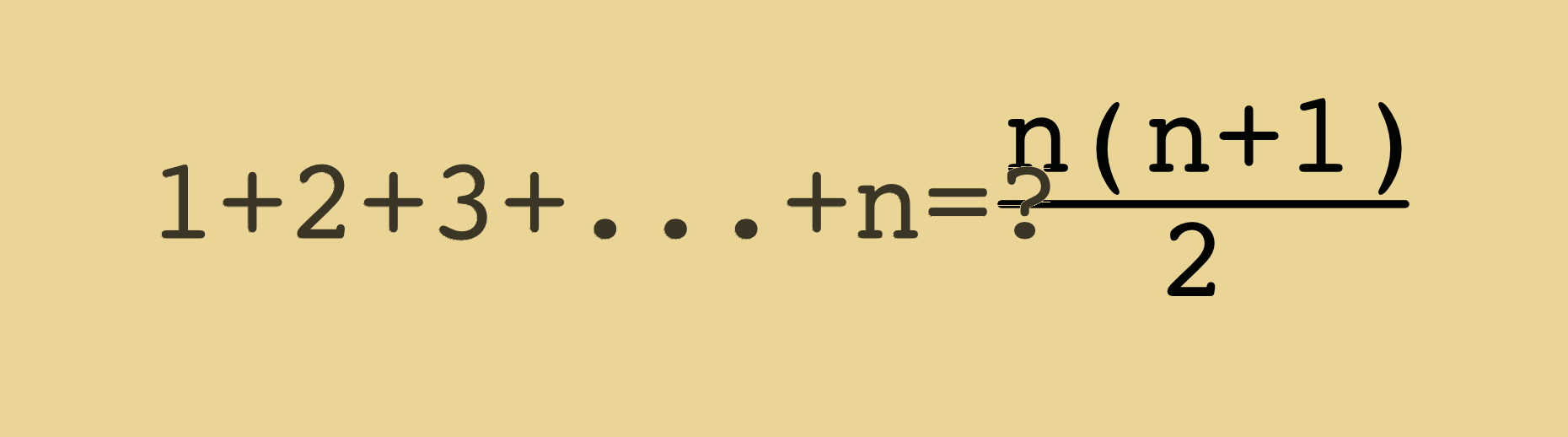
Problème 3 :
Excel numérote les colonnes avec des mots de une, deux, trois... lettres. Ainsi les colonnes $1,\ 2,\ 3$ sont numérotées $A,\ B,\ C$ sous Excel. La colonne $26$ est $Z$ . Ensuite on trouve $AA, AB, AC$ ... de même qu'après $ZZ$ , on trouve $AAA$ . Trouver à quoi correspondent les colonnes $10$ , $100$ , $1000$ et $2019$ en notation de colonne Excel. On poura commencer par calculer $26^2$ et $26^3$ en calcul mental.
On fournit la table de correspondance suivante :
A 1
B 2
C 3
D 4
E 5
F 6
G 7
H 8
I 9
J 10
K 11
L 12
M 13
N 14
O 15
P 16
Q 17
R 18
S 19
T 20
U 21
V 22
W 23
X 24
Y 25
Z 26
Aide : la colonne numéro $676$ est notée $YZ$ sous Excel et la colonne numéro $17576$ est notée $YYZ$ sous Excel... mais pourquoi ?
solution
Commençons par calculer, en calcul mental, comme demandé, $26^2$ et $26^3$ .
$26^2=(20+6)^2=400+2\times 20\times 6+36=436+4\times 6\times 10=436+240=676$ (comme dans l'aide).
$26^3=26^2\times 26=676\times (20+6)=13520+6\times 676=13520+4056=17576$ , comme dans l'aide également.
Pour la colonne numéro 10 :
La colonne numéro $ 10$ correspond directement à la notation $ J$ sous Excel parce qu'elle figure dans la table de correspondance.
Pour la colonne numéro 100 :
La division euclidienne de $ 100$ par $ 26$ fournit $100=3\times 26 + 22$ . Il s'agit donc d'un mot de deux lettres. La première (la plus à gauche) correspond à $ 3$ , c'est donc $ C$ et la seconde correspond à $ 22$ , c'est donc $ V$ . Au final, la notation Excel de la colonne $ 100$ est $ CV$ .
Pour la colonne numéro 1000 :
La division euclidienne de $ 1000$ par $ 26$ fournit $1000=38\times 26 + 12$ .
Comme $38=1\times 26 + 12$ , il suffit de reporter cette décomposition. Alors : $1000=38\times 26 + 12=(1\times 26 + 12)\times 26 + 12=1\times 26^2 + 12\times 26 + 12$ . Il s'agit donc d'un mot de trois lettres. La première (la plus à gauche) correspond à $ 1$ , c'est donc $ A$ . La deuxième et la troisième correspondent à $ 12$ , c'est donc $ L$ . Au final, la notation Excel de la colonne $ 1000$ est $ ALL$ .
Pour la colonne numéro 2019 :
La division euclidienne de $ 2019$ par $ 26$ fournit $2019=77\times 26 + 17$ .
Comme précédemment, on reporte la décomposition $77=2\times 26 + 25$ , soit : $2019=77\times 26 + 17=(2\times 26 + 25)\times 26 + 17=2\times 26^2 + 25\times 26 + 17$ . Il s'agit donc d'un mot de trois lettres. La première (la plus à gauche) correspond à $ 2$ , c'est donc $ B$ . La deuxième lettre correspond à $ 25$ , c'est donc $ Y$ . La troisième correspond à $ 17$ , c'est donc $ Q$ . Au final, la notation Excel de la colonne $ 2019$ est $ BYQ$ .
Pour la colonne numéro 676 :
La division euclidienne de $ 676$ par $ 26$ fournit $676=16^2=26\times 26 + 0$ .
Comme les lettres sont associées aux nombres à partir de $ 1$ , il faut remplacer le $ 26$ de gauche par $ 25+1$ .
$676=26\times 26 + 0=(25+1)\times 26 + 0=25\times 26 + 26$ . Il s'agit donc d'un mot de deux lettres. La première (la plus à gauche) correspond à $ 25$ , c'est donc $ Y$ . La deuxième lettre correspond à $ 26$ , c'est donc $ Z$ . Au final, la notation Excel de la colonne $ 676$ est $ YZ$ .
Pour la colonne numéro 17576 :
La division euclidienne de $ 17576$ par $ 26$ fournit $676=26^3=26\times 26^2 + 0$ .
Comme les lettres sont associées aux nombres à partir de $ 1$ , il faut remplacer le $ 26$ les plus à gauche par $ 25+1$ .
$17576=26\times 26^2 + 0=(25+1)\times 26^2 + 0=25\times 26^2 + 26^2 + 0$ .
Comme on ne doit pas avoir de reste $ 0$ , on recommence à décomposer le $ 26^2$ du milieu.
$17576=25\times 26^2 + 26^2 + 0=25\times 26^2 + (25+1)\times 26 + 0 = 25\times 26^2 + 25\times 26 + 25$ . Il s'agit donc d'un mot de trois lettres. La première (la plus à gauche) correspond à $ 25$ , c'est donc $ Y$ . La deuxième lettre aussi. La troisième lettre correspond à $ 26$ , c'est donc $ Z$ . Au final, la notation Excel de la colonne $ 17576$ est $ YYZ$ .
5. Jeux, énigmes, casses-têtes et tests de Q.I.
Suite numéro 1 :
Quelle est la suite «logique» de $1,3,2,5,4,7,6$ ?
Quel est la part d'ambiguité dans ce genre d'énoncé ?
solution
On peut sans doute penser les nombres sont inversés à partir de 2 : on a $3, 2$ au lieu de $2, 3$ , puis $5, 4$ au lieu de $4, 5$ et $7, 6$ au lieu de $6, 7$ , donc cela doit sans doute continuer par $9, 8$ .
Ce genre d'énoncés est parfois mal posé, volontairement ou non, comme pour l'énigme suivante dont la réponse est 1 + 1 + 5 -- sous entendu 1 (jour) + 1 (heure) + 5 (heures) :

Si l'énoncé ne dit pas explicitement quel modèle peut être utilisé, il peut y avoir plusieurs réponses. Par exemple, la suite $1, 2$ peut se compléter en $1, 2, 3$ ou en $1, 2, 4$ suivant qu'on décide d'utiliser des additions ou des multiplications.
Donner plus de termes ne résoud pas l'ambiguité. Ainsi $1, 2, 3, 4, 6$ admet plusieurs suites possibles, comme le montre l'OEIS.
Suite numéro 2 :
Quelle est la suite «logique» de bleu , $4$ ; rouge , $5$ ; oranges ?
solution
Une interprétation simple consiste à penser que le chiffre correspond au nombre de lettres. La réponse est alors $7$ parce qu'il y a 7 lettres dans le mot oranges.
Suite numéro 3 :
Quelle est la suite «logique» de $1, 1, 2, 3, 5, 8, 13, 21$ ?
solution
La réponse est $34$ car il s'agit de la fameuse suite de Fibonacci.
Suite numéro 4 :
Quelle est la suite «logique» de jambon , $1$ ; bateau , $2$ ; avantage , $3$ ; abracadabra ?
solution
Une interprétation simple consiste à penser que le chiffre correspond au nombre de a dans le mot. La réponse est alors $5$ parce qu'il y a 5 lettres a dans le mot abracadabra.
Suite numéro 5 :
Quelle est la suite «logique» de $1, 11, 21, 1211, 111221$ ?
solution
La réponse est $312211$ car il s'agit de la suite de Conway.
Suite numéro 6 :
Quelle est la suite «logique» de jambon , $624$ ; bateau , $642$ ; avantage ?
solution
Une solution possible consiste à dire que le nombre qui suit le mot correspond au nombre de lettres, suivi du nombre de voyelles suivi du nombre de consonnes. La réponse est alors $844$ .
Suite numéro 7 :
Quelle est la réponse à «la grande question sur la vie, l'univers et le reste» parfois résumée abusivement sous la forme polysémique « quel est le sens de la vie ?» ?
solution
La seule réponse, mi-comique, mi-sérieuse est bien sûr le nombre 42.
retour au plan de cours
|
 Retour à la page principale de
(gH)
Retour à la page principale de
(gH)