The Steiner-Tree problem is a minimization problem at its core (which is why it adapts well to a genetic-algorithm solution).

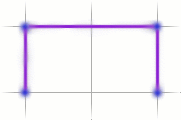
Consider a network, where the cost of the network is based solely on the length of the connections. So a network like this:

four-node network

costs 4 units (where spanning a grid costs one unit).

One method to find the minimal spanning tree is the "brute force method". The algorithm goes something like this:

  1. Find the two closest nodes. If connecting them doesn't cause a circuit, then do so.
  2. Repeat

Simple, no? A way of dealing with circuits is: begin with all the nodes uniquely labeled. Then, connect the two closest nodes (that have different labels) and replace the one label with the other. When you are finished, all the nodes will have the same label (i.e., they are all connected) and there will be no circuits.

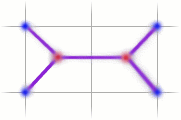
Matters are complicated when you add the possibility of Steiner points. Steiner points are like phantom nodes. They are added to the graph to shorten the connecting distance. For instance, by adding these two Steiner points we can shorten the path to 1 + 4 sqrt(1/2) = 3.83

four-node network with two steiner points

Figuring out how where to put these Steiner points is a non-trivial matter (NP-complete, actually).

In the problem we did, we were working with rectilinear coordinates. That means, that nodes could only exist at integer coordinates, such as (1,5) or (3,4) but not (2.3, 7). Also, the connections could only go verticle or horizontal. That is to say, the metric is:

distance(x1, y1, x2, y2) = abs(x1 - x2) + abs(y1 - y2)

So, in this example the steiner points could not reduce the cost (in rectilinear coordinates). Here's an example of a network that is helped by rectilinear steiner points:

Without Steiner points:
graph without steiner points
Cost = 18.

With Steiner points:
graph with steiner points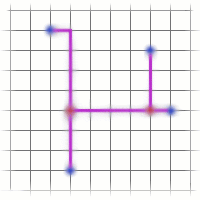
Cost = 16.

By Ian Bicking.