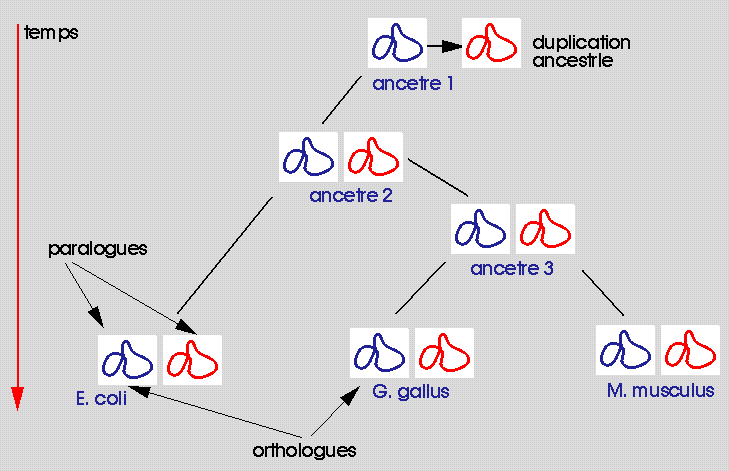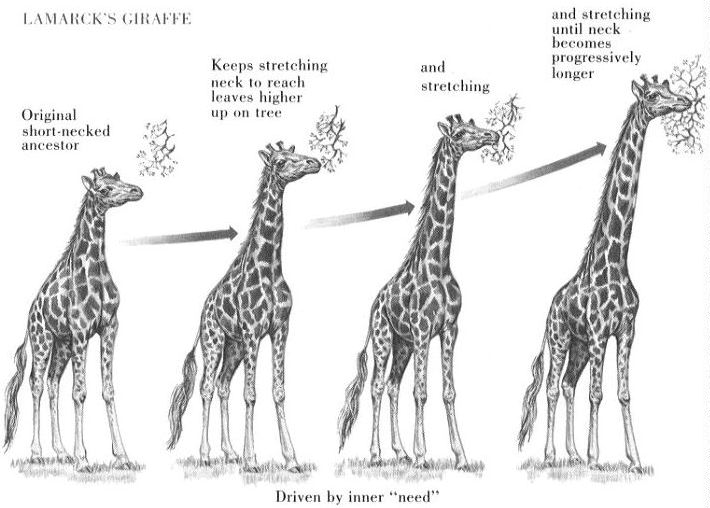
Figure 1 : l'évolution selon Lamark

Figure 1 : l'évolution selon Lamark
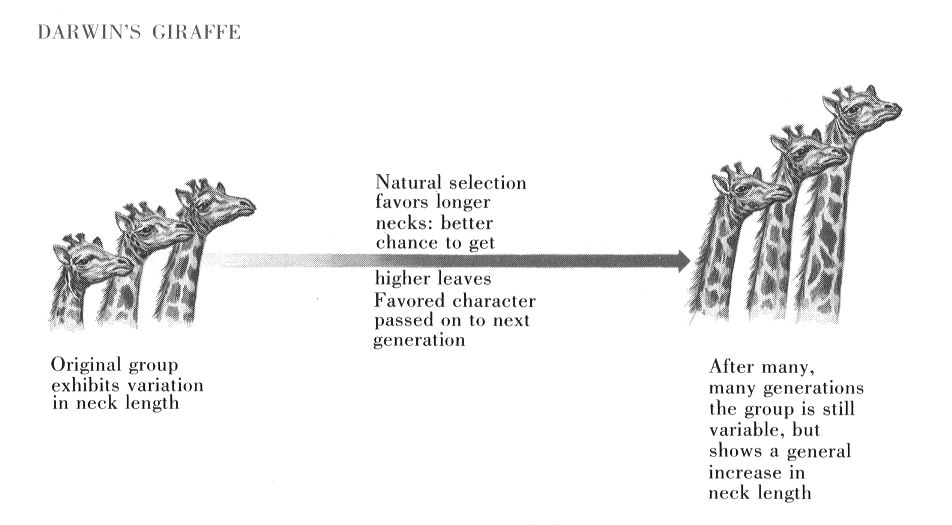
Figure 2 : l'évolution selon Darwin
|
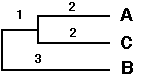
On clusterise tout d'abord les deux OTUs avec la distance la plus faible
(A et B). Le point de branchement est positionné à la distance
2/2=1.
On peut alors construire le sous arbre suivant :
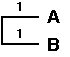
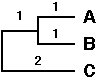
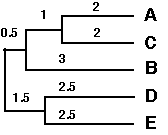
Dans la suite, le cluster (A,B) est considéré
comme un tout et on peut calculer une nouvelle matrice de distance :
dist(A,B),C = (distAC + distBC) / 2 = 4
dist(A,B),D = (distAD + distBD) / 2 = 6
dist(A,B),E = (distAE + distBE) / 2 = 6
dist(A,B),F = (distAF + distBF) / 2 = 8
|
|
|
|||||||||||||||||||||||||||||||||||||
| Cycle 1 |
|
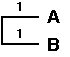 |
||||||||||||||||||||||||||||||||||||
| Cycle 2 |
|
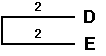 |
||||||||||||||||||||||||||||||||||||
| Cycle 3 |
|
 |
||||||||||||||||||||||||||||||||||||
| Cycle 4 |
|
 |
||||||||||||||||||||||||||||||||||||
| Cycle 5 |
|
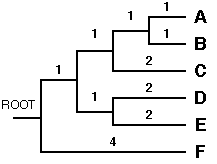 |
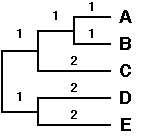
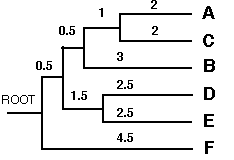
Cette méthode conduit essentiellement à unn arbre non enraciné. Si on veut enraciner l'arbre, on peut appliquer la méthode du "mid-point rooting" : la racine de l'arbre est à équidistance de tous les OTUs soit (ABCDE),F / 2 = 4
Les inconvénients de la méthode UPGMA
L'inconvénient majeur est la sensibilité de la méthode
à des taux de mutations différents sur les différentes
branches
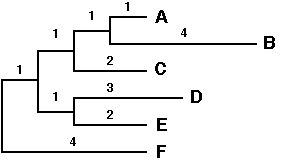
Supposons que l'on veuille reconstruire l'arbre suivant à
partir de la matrice de distances associée aux séquences
:
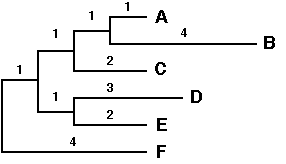
Depuis que A et B ont divergé, B a accumulé beaucoup plus de mutations que A
| MATRICE | ARBRE | |||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
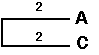 |
||||||||||||||||||||||||||||||||||||
|
|
|
 |
||||||||||||||||||||||||||||||||||||
|
|
|
 |
||||||||||||||||||||||||||||||||||||
|
|
|
 |
||||||||||||||||||||||||||||||||||||
|
|
|
Topologie Fausse !! |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|||
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Etape 1 : calcul de la divergence de chacun des N OTUs
par rapport aux autres (N= 6)
r (A) = 5+4+7+6+8 = 30
r(B) = 42
r(C) = 32
r(D) = 38
r (E) =34
r(F) = 44
Etape 2 : cacul de la nouvelle matrice en utilisant la
formule
M(i,j) = d(ij) -[r(i) + r(j)] / (N-2)
ce qui donne pour la paire AB : M(AB) = 5 - [30 + 42] / 4 = -13
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|||
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A
F |
B
\ |
/
\ | /
\ | /
/ | \
/ | \
/ |
\
E |
C
D
Etape 3 : Choix des plus proches voisins, c'est à
dire des deux OTUs ayant le M(i,j) le plus petit, donc soit A et B soit
D et E.
On prend A et B et on forme un nouveau noeud U et on calcule la longueur
de la branche entre U et A ainsi qu'entre U et B :
S (AU) = d (AB) / 2 + [r(A) - r(B)] / 2 (N-2) = 5/2 + [30-42] /2(6-4)
= 1
S(BU) = d (AB) - S(AU) = 5 - 1 = 4
Etape 4 : on définit les nouvelles distances entre
U et les autres OTUs
d (CU) = d(AC) + d (BC) - d(AB) / 2 = 3
d (DU) = d(AD) + d(BD) -d(AB) /2 = 6
d (EU) = d(AE) + d (BE) - d(AB) / 2 = 5
d (DU) = d(AF) + d(BF) -d(AB) /2 = 7
création d'une nouvelle matrice :
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Et d'un arbre en étoile :
C
D |
\ |
A
\__| ____1/
/ |
\
/ |
\ 4
E F
\
B
La procédure complète repart de l'étape 1 avec
N = N-1 = 5.
Types de substitutions
On distingue différents types de substitution suivant les bases
impliquées.
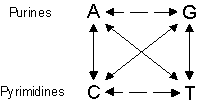 |
Transitions :
A <-> G, C <-> T Transversions : A <-> C, A <-> T, G <-> C, G <-> T |
Lorsque l'on compare deux séquences, on différencie aussi
les substitutions selon leur ordre et leurs conséquences.
|
|
|
substitutions observées |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
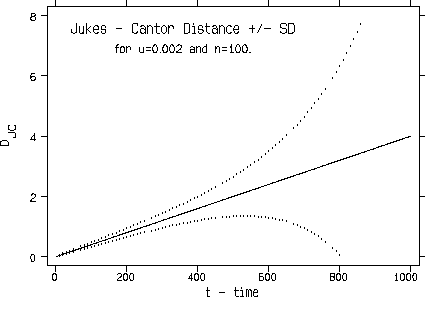
Exemples de corrections pour les substitutions multiples
- Correction de Jukes et Cantor (1969) : On fait l'hypothèse que tous les sites sont équivalents (tous les changements ont une probabillité égale mais elle varie au cours du temps), qu'il n'y a pas de biais dans la direction du changement et qu'il n'y a eu ni insertions ni délétions. C'est l'hypothèse la plus simple,mais pas forcément la plus correcte.
![]()
![]()
- Correction de Kimura ou 2 paramètres (1980) :
ce modèle est similaire au modèle de Jukes-Cantor mais on
fait l'hypothèse que le taux de transition est différent
du taux de transversion. Ce modèle a été développé
suite à l'obsevation que les transitions étaient souvent
beaucoup plus fréquentes que les transversions.
Si P est la fréquence des transitions et Q la
fréquence des transversions :
![]()
![]()
avec
![]() et
et ![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Exemple
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pour 4 séquences, il y a 3 arbres non enracinés possibles. Ces trois arbres sont analysés (recherche de la séquence ancestrale et comptage du nombre de mutations)
(1) AAGAGTGCA
AGATATCCA (3)
\ 4
/ 2
\ 4
/
AGCCGTGCG --- AGAGATCCG
Nombre de mutations : 10
/
\
/ 0
\ 0
(2) AGCCGTGCG
AGAGATCCG (4)
(1) AAGAGTGCA
AGCCGTGCG (2)
\ 1
/ 3
\ 5
/
AGGAGTGCA --- AGAGGTCCG
Nombre de mutations : 14
/
\
/ 4
\ 1
(3) AGATATCCA
AGAGATCCG (4)
(1) AAGAGTGCA
AGCCGTGCG (2)
\ 1
/ 3
\ 5
/
AGGAGTGCA --- AGATGTCCG
Nombre de mutations : 16
/
\
/ 5
\ 2
(4) AGAGATCCG
AGATATCCA (3)
L'arbre I est celui nécessitant le moins de mutations, c'est
donc le plus parcimonieux.
Cette analyse prend en compte tous les sites des séquences mais
l'analyse peut également se faire uniquement sur les sites informatifs,
c'est à dire quand à cette position il y a au moins 2 nucléotides
différents, représentés chacun dans au moins deux
séquences.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1) GGA
GGG (2)
\ 1
/ 1
\ 1
/
GGG - - - ACG
Nombre de mutations : 5
/ 1
\ 1
/
\
(3) ACA
ACG (4)
(1) GGA
ACA (2)
\ 2
/ 1
\ 0
/
GGG - - - ACG
Nombre de mutations : 6
/ 1
\ 2
/
\
(4) ACG
ACA (3)
Dans le cas de 4 séquences, un site informatif favorise seulement
un arbre : le site 5 favorise l'arbre I plus que les arbres II et III (il
supporte l'arbre I). L'arbre le plus parcimonieux est celui qui est supporté
par le plus grand nombre de sites informatifs.
Le maximum de parcimonie recherche l'arbre optimal et dans ce processus,
il est possible de trouver plusieurs arbres optimaux (= arbres ex-aequo
= configuration comptabilisant le même nombre minimal de substitutions
nécessaires pour passeer d'une séquence à l'autre
dans l'ensemble de l'arbre).
Afin de garantir de trouver l'arbre le meilleur possible, il faut faire
une évaluation de toutes les topologies possibles mais cela devient
impossible lorsque l'on a plus de 12 séquences.
Branch and Bound : cette méthode est dérivée du maximum de parcimonie, elle garantit de trouver le meilleur arbre mais sans évaluer tous les arbres possibles. Elle permet de traiter un plus grand nombre de séquences mais reste limitée.
Recherche heuristique : il y a un réarrangement des branches à chaque étape, cette méthode ne garantit pas de trouver l'arbre optimal.
Arbre consensus : comme la méthode du maximum de parcimonie peut conduire à trouver plusieurs arbres équivalents, on peut créer un arbre consensus (avec utilisation du bootstraping). Cet arbre consensus est construit à partir des noeuds les plus fréquemment rencontrés sur l'ensemble des arbres possibles.
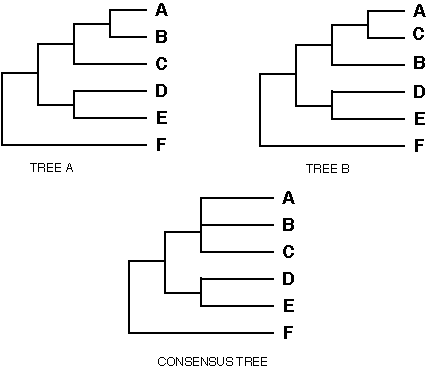
Avantages et inconvénients de la parcimonie
Avantages :
- Méthode basée sur les caractères : méthode
cladistique plutôt que phénétique.
- Méthode ne réduisant pas la séquence à
un simple nombre.
- Méthode essayant de donner une information sur les séquences
ancestrales.
- Méthode évaluant différents arbres.
Inconvénients :
- Méthode très lente par rapport aux méthodes
basées sur les distances.
- Méthode n'utilisant pas toute l'information disponible (seuls
les sites informatifs sont pris en compte)
- Méthode ne faisant pas de corrections pour les substitutions
multiples
- Méthode ne donnant aucune information sur la longueur des
branches
- Méthode connue pour être très sensible au biais
des codons
![]() Maximum
de vraissemblance
Maximum
de vraissemblance
Cette méthode de reconstruction phylogénétique
évalue, en terme de probabilités, l'ordre des branchements
et la longueur des branches d'un arbre sous un modèle évolutif
donné.
Programme DNAML
de Phylip
Exemple
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A partir des 4 séquences ci-dessus, on veut estimer la probabilité
que l'arbre A soit le bon, sous le modéle choisi.
(1)
(2)
\
/
\
/
----------
Arbre A
/
\
/
\
(3)
(4)
La vraissemblance de l'arbre est en général indépendante
de la position de la racine, on peut donc l'enraciner de manière
arbitraire :
1 2 3
4
\ / |
/
\ / |
/
\
| /
\
| /
\ | /
ACGT ?
La vraissemblance au site j :
C C A
G
\ / |
/
\ / |
/
ACGT? | /
\
| /
\
| /
\ | /
ACGT ?
La vraissemblance pour un site j est la somme des probabilités
de toutes les possiblités de reconstruction de l'état ancestral
sous le modèle choisi.
La vraissemblance de l'arbre A est en général évaluée
en sommant les logs des vraissemblances pour chaque site (la somme des
probabibilités est trop faible).
L'arbre du maximum de vraissemblance est celui avec la vraissemblance
la plus élevée.
Les modèles évolutifs
Les probabilités obtenues à chaque site dépendent
du modèle choisi et dans le modèle le plus simple
- on suppose que la probabilité de chaque changement est indépendante
des changements précédents (Modèle de Markov).
- on suppose que les probabilités de substitution ne changent
pas au cours du temps (le long de l'arbre).
- on suppose les changements réversibles : P(A -> T) = P(T ->
A).
On peut introduire d'autres paramètres dans le modèle
afin d'accroître son réalisme :
- des taux de substitutions différents pour chaque remplacement
(matrice 4*4 pour l'ADN ou matrice de substitution)
- une correction pour le nombre de sites suceptibles de muter et des
taux de substitutions variables pour ces sites.
- un taux de variation différents pour chaque site : on peut
par exemple utiliser une distribution statistique (distribution gamma)
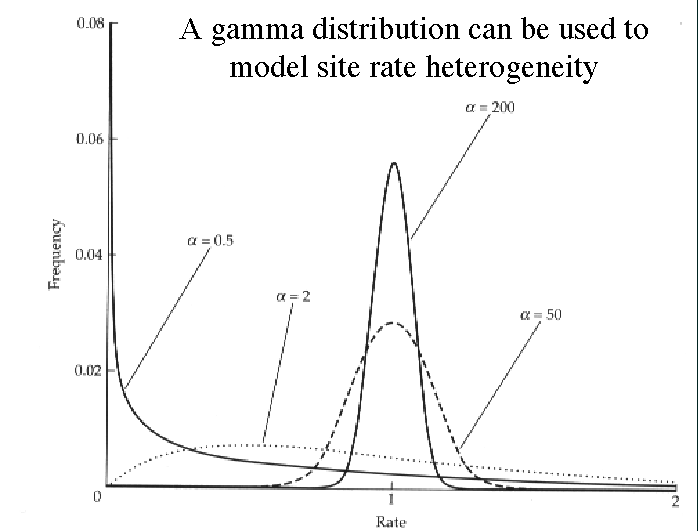
Il faut savoir que plus on introduit de paramètres, plus le calcul sera long et plus il y aura une accumulation de petites erreurs : il vaut mieux utiliser un modèle simple.
Le maximum de vraissemblance est une bonne méthode de reconstruction
phylogénétique mais il faut que le modèle de départ
corresponde bien aux données. Pour estimer les paramètres,
on peut utiliser une méthode plus rapide et utiliser l'arbre obtenu
pour fixer les paramètres de départ.
Cette méthode n'est utilisable que si on a un petit nombre de
séquences.
![]() Delete-half-Jackknifing
:
Delete-half-Jackknifing
:
Cette méthode, prônée par Wu (1986) ré-échantillonne
la moitié des sites des séquences et élimine le reste.
Cette méthode donne des résultats très similaire à
ceux obtenus par bootstrap.
![]() Permutation
:
Permutation
:
Cette méthode introduite par Archie (1989) et Faith (1990, Faith
et Cranston 1991)est basée sur la permutation des colonnes de la
matrice. Ce la produit des matrices ayant le même nombre de colonnes,
les mêmes caractères mais qui n'ont plus de structure taxonomique.
Cette méthode est utilisée dans un but différent par
rapport au bootstrap : elle teste l'hypothèse qu'il y a bien une
taxonomie dans les données actuelles.
| METHODES | SEQUENCES | AVANTAGES | INCONVENIENTS | PROGRAMMES | REMARQUES |
|---|---|---|---|---|---|
| Distances | Très proches | Rapides
Faciles à mettre en oeuvre |
Tous les sites sont traités de manière équivalente
d'où un perte d'informations
Non applicables à des séquences éloignées |
DNAdist | Il vaut mieux utiliser le Neigbor-joining plutôt
qu'UPGMA car Nj autorise des taux de mutations différents le long
des branches
Possibilité d'introduire des corrections |
| Parcimonie | Relativement éloignées | Evaluation de différents arbres
Essaie de donner des informations sur les séquences ancestrales |
Lente
Inutilisable lorsque l'on a un grand nombre de séquences |
DNApars | On peut obtenir plusieurs arbres équivalents et dans ce cas le choix de l'un par rapport aux autres peut être difficile à justifier |
| ML | éloignées | Robuste
taux de transisitions/transversions différents Estimation de la longueur des branches de l'arbre final |
Lente
Inutilisable lorsque l'on a un grand nombre de séquences |
FastDnaml |