SAC

:

Stockage, Archivage et Compression partie 3 / 3 : Compression  (gh)

 

Que faut-il comprimer (ou "compresser") ?

A cette question, comme à celles qui suivent, il n'y a pas de réponse qui conviendrait à toutes les situations. S'il faut en général compresser les fichiers lorsqu'on paie le cout des transmissions ou lorsque les fichiers sont "gros", la production en masse de gros disques (300 Go pour une centaine d'euros en 2005) et le faible cout des DVD simple couche de taille 4,7 Go (quelques €) et des graveurs de DVD (une centaine d'euros) permettent de s'affranchir de la compression dans de nombreux cas. Sous XP, il est possible [mais pas forcément conseillé] de compresser automatiquement les fichiers pour gagner de la place : La compression va en général de pair avec l'archivage ce qui permet de gérer de nombreux fichiers à la fois, avec des noms de répertoire, de sous-répertoire... L'usage veut que des sauvegardes nombreuses (par exemple journalières) soient volumineuses, ce qui incite souvent à compresser... On adjoint éventuellement à l'archivage et à la compression du chiffrement (improprement nommé "cryptage" en langage courant) pour garantir la sécurité des données...

Quels formats de compression utiliser ?

Là encore il n'y a pas de réponse toute faite. Le plus important à se rappeler est qu'un fichier compressé n'est utile que si on sait le décompresser. Donc souvent on utilise un format multi-systèmes comme zip et ses avatars (arc, rar, 7z...) quand on est sous Windows ou sous Unix, un format comme tgz qui est un format "tar" compressé lorsqu'on est depuis longtemps sous Unix... Les formats MacIntosh sont pratiques pour les habitants de MacIntoshie mais ne sont pas conseillés lorsqu'on met des documents à disposition sur le Web sous forme d'archives compressées car leurs décompressions requierent des décompresseurs spécialisés comme stuffit pour Linux ou stuffit pour Windows qui ne sont pas disponibles en standard sur la plupart des ordinateurs. Le format zip, par contre, a été intégré au système d'exploitation XP et ne requiert -- en principe -- aucun autre logiciel de compression. Il est depuis longtemps disponible sous Unix. Si par contre on recherche un format "exotique" non reconnu par tout le monde, on peut écrire son propre format ou se contenter de renommer les fichiers. Ainsi, renommer cours.zip en cours.ckr rend le fichier "non double-cliquable" sauf à savoir qu'il s'agit d'une archive compressée au format zip.

Quels compresseurs utiliser ?

Pour des utilisations peu fréquentes, les commandes contextuelles des explorateurs sous Linux sont suffisantes et un outil gratuit en mode fenêtré sous Windows sans doute un bon choix, comme 7-zip. Si le fameux winzip est payant, d'autres logiciels comme winace, winrar ou powerarchiver font en gros aussi bien et à moindre cout. Pour un usage plus soutenu, la compression en ligne de commande se révèle souvent nécessaire, pour Unix comme pour Windows que ce soit avec compress, zip, gzip ou winzip (en "add-on"). Comme le montrent les pages de manuels pour les commandes compress, zip et gzip les options, nombreuses, offrent toute la souplesse que l'on est en droit d'exiger pour des opérations de sauvegarde et d'archivage : gzip [-cdfhlLnNrtvV19] [-S suffix] [file ...] unzip [-Z] [-opts[modifiers]] file[.zip] [list] [-x xlist] [-d exdir] zip [-options] [-b path] [-t mmddyyyy] [-n suffixes] [zipfile list] [-xi list] Signalons au passage que pour zip l'option -x (pour exclude) permet de ne pas compresser certains fichiers, que l'option -d (comme destination) pour unzip permet de préciser le dossier où extraire les données et que l'option -u (comme update) aussi pour unzip permet de mettre à jour les fichiers existants [et de créer les nouveaux fichiers si nécessaire]. Si on s'intéresse à l'interopérabilité multi-systèmes (!) c'est à dire si on doit souvent compresser, transférer puis décompresser des archives d'un système d'exploitation (Windows, Linux...) à l'autre, des options de conversion pour les "sauts de ligne" sont disponibles. Un logiciel fenêtré récent comme 7-zip supporte même Unicode et sa version ligne de commande pour Linux nommée p7zip permet de transférer des fichiers dont les noms contiennent des caractères accentués....     Pour les fanatiques du "tout construit à la main et modifiable", signalons une interface pour tar, zip, gzip, bzip2... écrite en Tcl/Tk nommée TkZip qui présente aujourd'hui (2005) peu d'intérêt car de nombreux explorateurs de fichiers sous Windows comme sous Linux intégrent un décompresseur de fichiers tar, zip etc.

Comment s'effectue une compression ?

On peut distinguer deux types de compression : la compression sans perte où décompresser redonne les informations initiales (par exemple pour les données numériques, les fichiers de traitement de texte) et la compression avec perte (par exemple pour les images, les vidéos et les sons) où la décompression du fichier ne redonne pas le fichier original mais pour lesquelles les différences sont "acceptables" (l'oeil ou l'oreille ne voient pas les différences). De nombreux formats de données numériques sont aujourd'hui des formats compressés. Une compression naive compte les caractères et stocke le facteur de répétition (méthode RLE). Les méthodes statistiques ("méthode Huffman") attribuent une longeur de bit plus courte aux motifs les plus fréquents alors que les méthodes de de type dictionnaires ("méthode Lempel-Ziv-Welch") utilisent dynamiquement des successions de caractères qui se ressemblent. Un exposé élémentaire sur la compression est celui de David K. Every, traduit de l'anglais par Charles Giguère sur le site VDN (Articles informatiques & vulgarisation). Une version plus détaillée est celle de Sylvain RENARD proposée par le site "la tour des ruses" dans le cadre d'une conférence à un club Photoshop et qui est un texte assez général quoiqu'orienté image (version pdf locale). Un cours traditionnel sur les algorithmes de compression est celui de Christophe GONZALES qui comporte une centaine de pages (version PDF locale). Pour les images, la notion de compression fractale et de compression par ondelettes devrait sans doute encore beaucoup progresser et devenir un "nouveau" standard comme les formats mp3, mpeg4, et divx le sont devenus pour les sons, musiques et vidéos dans les années 2000.

Compression "à la carte" par formule mathématique

Les techniques automatiques de compression sont statistiquement efficaces. Le fait qu'elles soient disponibles par logiciel les rendent faciles à utiliser mais elles ne constituent pas forcément le meilleur choix pour stocker des renseignements. Imaginons par exemple que l'on doive conserver les cent cinquante mile valeurs 1 3 5 7 9 11... 299999 La compression maximale est certainement A 2 1 150000 ce qui signifie suite Arithmérique de raison 2 de premier terme 1 avec 150000 valeurs. Il s'agit d'une compression sans perte que l'on pourrait étendre aux suites de valeurs linéairement récurrentes (voir par exemple la page vsrlpost pour générer de telles suites). Le problème posé ici est de trouver une formule pour redonner les valeurs (si tant est qu'elle existe), ce qui ne semble pas être un problème mathématique facile. Notre programme esrl y arrive cependant dans un certain nombre de cas... Pour une compression avec perte, on peut -- lorsqu'on travaille globalement sur des valeurs numériques -- se contenter des résumés statistiques classiques (nombre de valeurs, moyenne, écart-type...) à moins qu'on ne soit capable de détecter une loi classique. Ainsi les valeurs 25 25 25 24 26 25 25 25 sont suffisamment proches d'une loi uniforme pour qu'on puisse sans trop se tromper les réduire aux paramètres n=8, m=25, s=0.5 soit encore l'expression "probabiliste" U 1 8 200. On pourra s'en convaincre avec la page des lois discrètes usuelles. 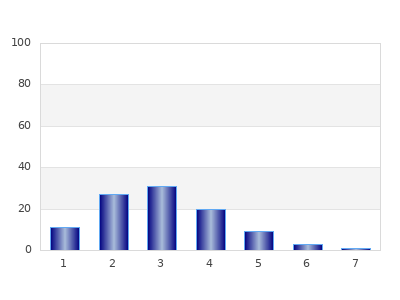Par contre, il est beaucoup moins évident qu'on peut remplacer les données 43 106 122 80 37 10 2 par l'expression B 10 0.2 400 à moins de bien connaitre la recherche de lois statistiques et les tests d'adéquation pour quantifier la "qualité" de compression par cette loi binomiale de paramètre n=10 et p=0.2 pour une population totale de 400 individus, ou sauf à afficher l'histogramme associé...

Comment personnaliser ou automatiser les compressions ?

Il suffit d'apprendre à manipuler les logiciels ou commandes en ligne de commande puis d'utiliser un langage interprété, voire graphique comme Rexx, Perl, Tcl /Tk. Ainsi le programme sovcd.pl sauvegarde dans le fichier toutxxx.zip tous les fichiers du répertoire courant et des sous-répertoires sauf les fichiers zip présents où xxx est incrémenté de 1 à chaque sauvegarde (la première fois, la sauvegarde est nommée tout001.zip, la seconde fois tout002.zip etc.). De même, le programme sovcd.rex sauvegarde tout le répertoire courant et ses sous-répertoires en mettant comme nom d'archive compressée le nom du répertoire. Par exemple si on est dans /home/info/gh/public_html/Farcomp/ le programme sauvegarde dans Farcomp.zip ; le petit frère de ce programme est getcd.rex qui décompresse automatiquement... Voici un exemple d'utilisation : @sirius~/public_html/Farcomp|(~gH) > regina ~/Bin/sovcd updating: sac3.htm (deflated 65%) updating: sacex.htm (deflated 66%) adding: comprdsq.png (deflated 8%) adding: compresseurs.png (deflated 3%) ... vous pouvez utiliser Farcomp.zip -rw-r--r-- 1 gh info 10722916 nov 16 17:23 Farcomp.zip # après transfert de Farcomp.zip sous Windows par [s]ftp : W:\Farcomp>regina x:\getcd.rex getcd.rex : recuperation des fichiers du chemin courant ... on lit dans Farcomp.zip Essai de : P:\WinZip\WZUNZIP.EXE -n -d Farcomp.zip WinZip(R) Command Line Support Add-On Version 1.1 SR-1 (Build Copyright (c) WinZip Computing, Inc. 1991-2004 - All Rights R Zip file: Farcomp.zip skipping .\agenda.txt -- no update needed skipping .\alldsc1.txt -- no update needed skipping .\alldsc2.txt -- no update needed skipping .\alldsc.pl -- no update needed skipping .\alldsc.rtf -- no update needed unzipping mangzip.txt ... Pour une interface graphique simple liée aux commandes de compression, on peut utiliser l'exemple proposé pour l'archivage avec ses boutons décrite dans la section 2 en remplaçant "tar" par "zip"...

 

Exercices associés à cette page

 

 

   Retour à la page principale de   (gH)